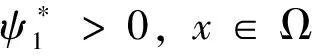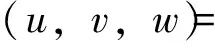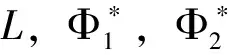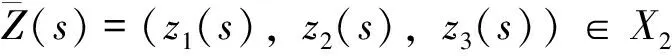一类蜘蛛-昆虫模型平衡态正解的存在性*
2016-06-05姜洪领
姜洪领
(宝鸡文理学院数学与信息科学学院,陕西 宝鸡 721013 )
一类蜘蛛-昆虫模型平衡态正解的存在性*
姜洪领
(宝鸡文理学院数学与信息科学学院,陕西 宝鸡 721013 )
研究一类单食饵-双捕食者的蜘蛛-昆虫模型。利用特征值变分原理和极值原理给出正解的先验估计及正解存在的必要条件。应用空间分解和隐函数定理得到正解存在的充分条件。结果表明,在特定条件下, 系统共存态依赖于昆虫的生长率。
蜘蛛-昆虫模型;平衡态正解;存在性
利用特定物种进行农业生态系统管理是一个很有意义的课题[1-3]。文[4-5]讨论了如下用ODE刻画的Spider-insect系统
(1)
其中p(t)表示昆虫密度,sw(t),sc(t)表示两类蜘蛛密度,r表示昆虫p(t)的内禀增长率,μw和μc分别表示sw(t)和sc(t)的死亡率。a,b分别表示sw(t)和sc(t)的捕食率。所有参数都是正常数,详细生物意义见文[5]。文[4]研究了(1)含有时滞时平衡态正解的有界性,局部稳定性以及其产生的Hopf分歧。文[5]研究了非时滞系统的持久性和全局稳定性,同时也研究带时滞系统的全区稳定性及其Hopf分歧。需要注意的是,模型(1)是在忽略文献[1-2]提出的蜘蛛会在其属地(livinghabitats)内迁移的情况下建立的。这种迁移会导致物种在空间的不均匀分布,并且这种不均匀分布可能影响系统的生态动力学行为。因此利用扩散来模拟这种行为[6-7]。为了便于后面的书写,利用下列无量纲变量
并且沿用不带‘-’的记号,(1)可化为如下带有齐次Dirichlet边界条件的反应扩散方程组
初值条件为
其平衡态系统为如下椭圆型方程组
(2)
其中u表示昆虫的密度,v,w表示蜘蛛的密度,β表示昆虫的内禀生长率,γ,δ表示蜘蛛的死亡率。Ω为RN的具有光滑边界的有界开区域,Δ项表示物种的扩散项。显然系统(2)中的参数都是正常数。本文与文 [8-10]有着明显的不同。在文[8]中,作者研究的是一个捕食者两个食饵情形,在文[9-10]中,作者研究的是三物种竞争模型。
本文主要讨论系统(2)正解的先验估计、存在正解的必要条件。同时利用空间分解结合隐函数定理给出正解存在的条件。
1 正解的先验估计和存在的必要条件
首先介绍两个记号。
记λ1(q)为
(i) 若q1(x)≥q2(x)且q1(x) ≢q2(x),则λ1(q1)>λ1(q2)。
(ii)对任意实数m,λ1(m)=m+λ1,这里,λ1=λ1(0)。
记θβ为
(3)
定理1 若系统(2)存在非负解(u,v,w)使得u≢0,则β>λ1,u<β。 进而
证明 记φ1>0是对应λ1的主特征函数,对系统(2)中第一式两边同乘φ1并积分可得
-∫Ωφ1Δudx=∫Ωφ1u(β-u-v-w)dx<β∫Ωφ1udx
由
得
从而β>λ1。
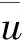
因此本文始终假设γ 定理2 任意系统(2)的正解(u,v,w) (若存在)必满足 证明 由定理1知β>λ1,u<β,容易验证β,u分别是 (3) 式的有序上解和下解,从而利用标准的上下解方法结合θβ的惟一性即有u<θβ。 定理3 对任意给定的a,b>0,存在β0>λ1,使得β>β0时, 证明 由文[11]中第二章论述可知 对任意的x∈Ω0⊂⊂Ω。 因此利用主特征值性质有 从而对任意给定的a,b,存在β0>λ1,当β>β0时使得左端成立。利用性质(i)和(ii)以及θβ<β可知 同理可得-λ1(-bθβ) 令 其中 记L为(2)在(γ*,δ*,θβ,0,0)处关于(u,v,w)的线性化算子,这里γ*,β*由定理3给出。直接计算可知 L= (4) 则L(φ,ψ,χ)=0等价于 简单计算可知 (5) 这里 (6) (7) 设L*为算子L的伴随算子,则L*(φ,ψ,χ)=0等价于 注意到λ1(2θβ-β)>0,有φ≡0。所以 (8) 其中 (9) 利用Fredholm选择公理结合(8)式可知 (10) 综合(5) 式,(8) 式有 dimN(L)=codimR(L)=2 所以不能应用基于单重特征值的Crandall-Rabinowitz分歧定理。受文献[13]的启发,我们应用空间分解和隐函数定理来讨论系统(2)发自点(γ*,δ*,θβ,0,0)处的分歧解,即就是下面的定理。 定理 4 对给定的a,b,c,d,当β>β0时,(γ*,δ*,θβ,0,0)是系统(2)的一个分歧点,即在(γ*,δ*,θβ,0,0)的邻域内系统(2)存在正解 (11) 其中 则(u,v,w)是系统(2)的正解等价于(u-θβ,v,w)是H(γ,δ,U)=0的满足u-θβ<0,v>0,w>0的解。容易验证 H(γ,δ,0)≡0,对任意的γ,δ∈R; HU(γ*,δ*,0)=L,L由(4)式给出 现将空间X,Y做如下正交分解 其中N(L),N(L*),R(L)分别由(5)式,(8)式,(10)式给出;Φ1,Φ2由(6)式给出。故可将任意的U∈X写成 (12) 利用(11)式简单计算可得 其中 以及 i) 当τ1=τ2=s=0,Z=(0,0,0)时, 由(7)式可知上式为零。同理计算可得 所以我们有H1(0,0,0,0)=0。 ii) 令D(Z,τ1,τ2)H1(0,0,0,0)为算子H1在(0,0,0,0)处关于(Z,τ1,τ2)的导算子, 则 (13) 代回到(12) 式可知 是H(γ,δ,U)=0的解。 注1 定理4表明,在蜘蛛的捕食率(即参数a,b)确定的条件下,存在常数β0>λ1,使得昆虫的生长率β大于β0时,只要蜘蛛的生长率γ,δ分别在γ*,δ*附近,系统存在共存态。由于γ*=-λ1(-aθβ),δ*=-λ1(-bθβ)。所以在上述条件下,系统的共存态最终依赖于昆虫的生长率。 [1]NTONIFORNN,PQRRMC,EWUKEMJAEwunkem.Seasonalabundanceanddistributionofthehuntsmanspider,Heteropodavenatoria(Sparassidae: Araneae) in banana agro-ecosystems in Cameroon [J]. Journal of Entomology, 2012, 9: 79-88. [2] VENKATESHALU, HANUMANTHRAYA L, MARADDI G. Impact of different rice agro-ecosystem on spider population dynamics [J]. Environment and Ecology, 2009, 27(3A): 1231-1236. [3] VENTURINO E, ISAIA M, BONA F, et al. Modeling the spiders ballooning effect on the vineyard ecology [J]. Mathematical Modeling of Natural Phenomena, 2006, 1(1): 137-159. [4] CHATTERJEE S, ISAIA M, VENTURINO E. Effects of spiders predational delays in intensive agroecosystems [J]. Nonlinear Analysis: Real World Applications, 2009, 10: 3045- 3058. [5] SEN M, BANERJEE M, VENTURINO E. A model for biological control in agriculture [J]. Mathematics and Computers in Simulation, 2013, 87(1): 30-44. [6] 王利娟, 姜洪领. 一类捕食食饵模型正解的定性分析和数值模拟[J]. 中山大学学(自然科学版), 2015, 54(4): 55-62. [7] 姜洪领, 王利娟. 一类无搅拌Chemostat模型平衡态正解存在性与数值模拟[J]. 中山大学学报(自然科学版), 2011, 50(3): 11-16. [8] WEI F. Coexistence, stability, and limiting behavior in a one-predator-two-prey model [J]. Journal of mathematical analysis and applications, 1993, 179(2): 592-609. [9] DANCER E N, DU Y H. Positive solutions for a three-species competition system with diffusion-I. General existence results [J]. Nonlinear Analysis Theory Methods & Applications, 1995, 24(3): 337-357. [10] DANCER E N, DU Y H. Positive solutions for a three-species competition system with diffusion-II. The case of equal birth rates [J]. Nonlinear Analysis Theory Methods & Applications, 1995, 24(3): 359-373. [11] DU Y H, LOU Y. Some uniqueness and exact multiplicity results for a predator-prey model [J]. Transactions of the American Mathematical Society, 1997, 349(6): 2443-2475. [12] WANG L J, JIANG H L, LI Y. Positive steady state solutions of a plant-pollinator model with diffusion [J]. Discrete and Continuous Dynamical Systems-Series B, 2015, 20: 1805-1819. [13] YAMADA Y. Stability of steady states for prey-predator diffusion equations with homogeneous Dirichlet conditions [J]. SIAM Journal on Mathematical Analysis, 1990, 21(2): 327-345. The existence of steady-state positive solutions for a spider-insect model JIANGHongling (Baoji University of Arts and Sciences, Institute of Mathematics and Information Science,Baoji 721013, China) A one-prey-two-predator spider-insect model is studied. By the variational principle of eigenvalue and the Maximum principle, priori estimates and the necessary conditions of existence for positive solutions are given. Applying the method of space decomposition and implicit function theorem, a sufficient condition of existence of positive solutions is obtained. The results show that, under certain conditions, the coexistence depends on the growth rate of insects. spider-insect model; steady-state positive solution; existence 10.13471/j.cnki.acta.snus.2016.03.011 2015-11-24 国家自然科学基金资助项目(11401356,11501496);宝鸡文理学院重点科研资助项目(ZK15038) 姜洪领(1978年生),男;研究方向:应用偏微分方程;E-mail:jhonglings@163.com O A 0529-6579(2016)03-0064-05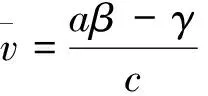
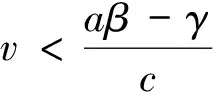
2 正解的存在性