基于空间六自由度机械臂的逆运动学数值解法
2016-06-05张栩曼张中哲王燕波
张栩曼,张中哲,王燕波,杨 涛,邓 涛
基于空间六自由度机械臂的逆运动学数值解法
张栩曼,张中哲,王燕波,杨 涛,邓 涛
(北京精密机电控制设备研究所,北京,100076)
针对解析法只能用于特殊构型的机械臂且求解过程复杂、计算量大的问题,提出一种适用于大多数串联型机械臂的数值迭代逆运动学求解方法。利用该方法,求解自主研发的空间六自由度机械臂的运动学逆解,并通过仿真证明该方法的可靠性。
空间机械臂;数值迭代;正逆运动学
0 引 言
机械臂正运动学和逆运动学的求解是机械臂实际控制中需要解决的基本问题。其中逆运动学的求解比正运动学的求解更加复杂,对于不同的机械臂构型没有标准的求解方法和步骤。一般机械臂逆运动学的求解方法主要有解析法、数值迭代法、几何法等。
解析法的优势在于使用该方法可以求解出所有的根,还可以证明根不存在的情况;缺点在于这种方法一般都非常的繁琐,需要大量的计算。数值迭代法的优势在于使用这种方法计算相对简单,可以求解出大部分机械臂的逆解[1],但每次迭代在给定预期初值的情况下,最终只能获得一组解,如果解不存在,数值迭代将无法收敛。几何法可以对某些特殊的臂型进行简化,并利用几何关系求解,但是它一般需要和解析法配合使用[1~3]。
Pieper证明了有相邻的3根关节轴交于一点的六自由度机械臂存在封闭解[4]。Duffy证明了有相邻3根关节轴平行的六自由度机械臂存在封闭解[5]。现在市场上的工业机器人几乎都有3根相交轴,一般都可以利用解析法求得所有的封闭解,再采用其他方法从中选取一组较优的可行解[6]。姜宏超等[7]针对六自由度模块化机械臂利用解析法求解出了全部逆解。李宪华[1]、刘金存[2]、张金涛[3]都是利用解析法和几何法结合的方法求解出了六自由度机械臂的全部逆解。但是对于一些不是此种构型的、难以用解析法求其逆解的机械臂,需要一种比较通用的求解方法。
本文所研究的空间机械臂固连在飞行器本体上组成空间机器人,用于实现空间碎片抓捕、在轨服务等任务。空间机械臂工作在失重的环境中,关节转动惯量不会由前级向后级累加,因此设计成由6个相同的模块化关节和臂杆连接组成的模块化六自由度空间机械臂。由于本文空间机械臂安装范围、重量指标的限制以及工作范围的要求,机械臂无法设计成有3根相交轴的结构,因此采用图1所示的特殊构型。该构型在逆运动学的求解问题上存在一定的难度和特殊性,使用解析法计算难以找到一组独立不相关的变量。因此本文使用一种数值迭代的方法求其运动学逆解。

图1 空间机器人
1 正运动学模型的求解
1.1 运动学模型的建立
要研究机械臂的运动,就必须建立它的运动学模型,再通过运动学模型求解正、逆运动学。一般通过建立关节坐标系,用数学方法抽象机械臂实体,描述机械臂相对基坐标系的位置和姿态。本文使用通用的D-H参数运动学建模法建模。空间六自由度机械臂构型如图2a所示,连杆坐标系的建立如图2b所示,其中基坐标系{0}与坐标系{1}重合,{6}为空间机械臂腕部坐标系。D-H参数表如表1所示。
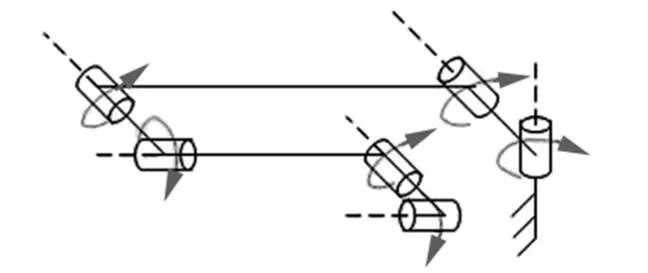
a)机械臂构型
b)连杆坐标系
图2 机械臂运动学建模
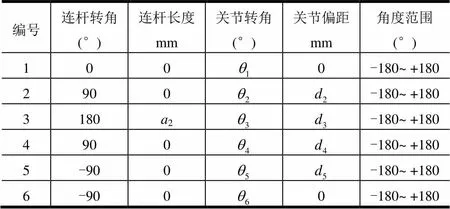
表1 六自由度空间机械臂D-H参数表
1.2 正运动学求解
空间六自由度机械臂正运动学的求解问题就是已知机械臂各关节角度值{,,,,,},求解机械臂腕部坐标系相对基座标系的位姿。表1定义了空间六自由度机械臂的所有连杆参数{,,,},其中只有参数是变量,其余均为常量。由连杆参数可以确定连杆坐标系{}相对于坐标系{-1}的齐次变换矩阵。

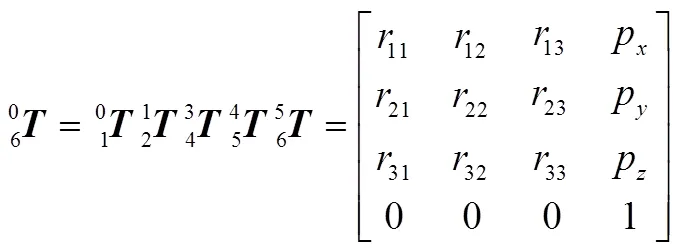
2 逆运动学求解
空间六自由度机械臂逆运动学求解的问题即已知腕部坐标系{6}相对基座标系{0}的期望位姿,即已知,求解达到这一位姿时6个关节转角{,,,,,}的值。逆解可能不存在,也可能有多重解或者只有一个解。
针对本文六自由度空间机械臂,利用牛顿迭代法[8]求解其运动学逆解。首先需要构建非线性方程组:,,
已知最终所需腕部坐标系{6}相对于基坐标系{0}的齐次变换矩阵,对于每一轮迭代也可得到一个齐次变换矩阵,为迭代次数,。将两矩阵中的元素一一相减得方程组:

即
由式(3)可以确定此方程组的雅克比矩阵为
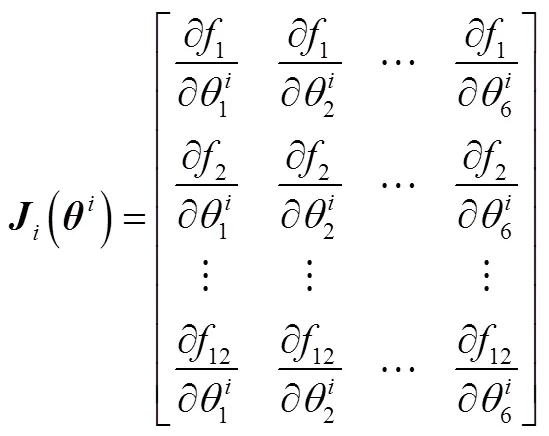
求解方程组的牛顿迭代公式为
(5)
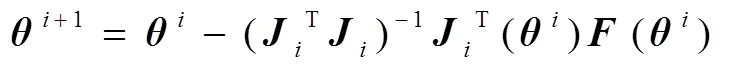
因此,可以利用式(6)求解六自由度空间机械臂的逆运动学。
3 仿真验证
3.1 正运动学验证
空间六自由度机械臂臂型2=3=5=164.5 mm,4=444.5 mm,2=610 mm。为了验证上述正运动学模型的正确性,按照式(2)在Matlab中编写程序。程序输入条件为六自由度空间机械臂各关节角~,输出条件为腕部坐标系相对于基坐标系的齐次变换矩阵。根据图2b所示坐标系间的几何关系,可确定空间机械臂处于折叠状态时腕部坐标系相对于基坐标系的齐次变换矩阵为,空间机械臂处于折叠状态时各关节角度值为。将此组角度值输入正运动学求解程序,可得。证明上文所得正运动学模型的正确性。
3.2 逆运动学验证
为了验证本文所述逆运动学求解方法的正确性和可靠性。在Matlab中编写逆运动学求解程序和运动规划程序,对一条指定直线进行轨迹跟踪,并在三维空间中作出规划轨迹和仿真轨迹,对规划轨迹位置点和仿真轨迹位置点的位置进行对比。
按照式(6)在Matlab中编写逆运动学求解程序,程序输入条件为初始角和期望达到位姿的齐次变换矩阵,输出为达到期望位姿时各关节角的值以及利用正运动学解求得的齐次变换矩阵。算法流程如图3所示。
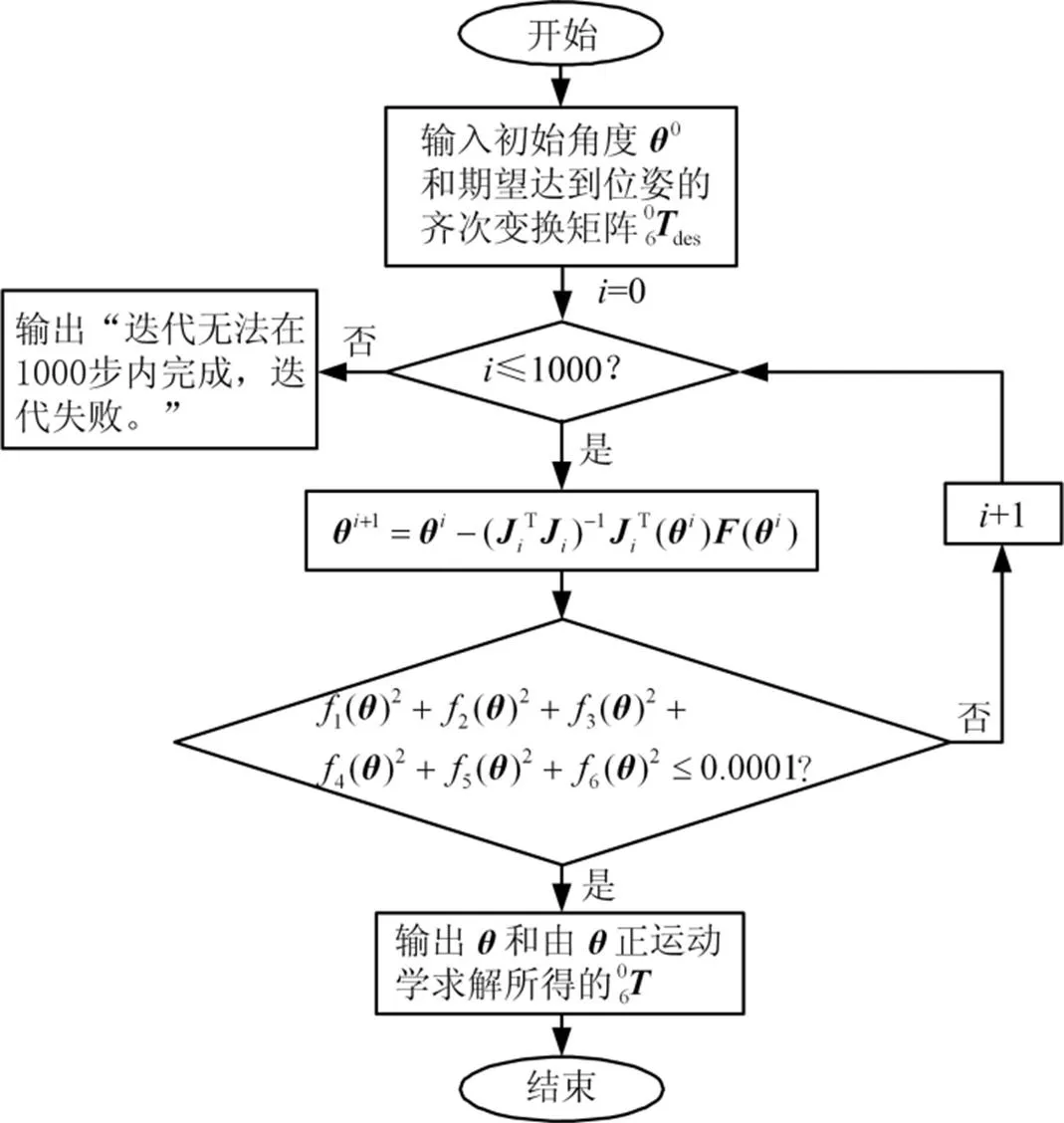
图3 逆运动学求解程序算法流程
假设空间机械臂运动控制器每20 ms给关节控制器发送一组关节角度值,即每20 ms运动控制器要根据运动规划进行一次逆运动学解算。假设机械臂末端速度为0.05 m/s,则每20 ms的时间间隔内空间机械臂末端的运动距离只有1 mm。因此,为了方便逆运动学解算的进行,以逆运动学求解算法为基础编写运动规划程序,将前一次迭代所得和中的旋转矩阵作为后一次迭代的初始输入。
位置追踪结果如图4所示,求解出的各关节角度值如图5所示。
由仿真结果可知,本文所用逆运动学求解方法能够正确可靠地求解出六自由度空间机械臂的逆解,并且能够有效地对腕部坐标系原点进行轨迹跟踪。
4 结束语
由于本文自主研发空间六自由度机械臂的特殊性,利用解析法求解机械臂逆运动学非常复杂,难以找到一组完全独立的变量,因此使用牛顿数值迭代法求解六自由度机械臂逆解。利用D-H运动学建模法建立六自由度机械臂正运动学模型。利用机械臂腕部坐标系{6}相对于基坐标系{0}的齐次变换矩阵构建非线性方程组,通过牛顿迭代,使每次迭代所得齐次变换矩阵无限接近期望位姿的齐次变换矩阵,最终迭代收敛得到期望关节角。并通过仿真实验证明正运动学和逆运动学求解方法正确可靠。本文提出的机械臂逆运动学数值迭代解法对于解析法难以求解运动学逆解的多自由度串联型机械臂均适用,可以有效地求解出机械臂运动学逆解,也为机械臂轨迹规划和控制提供了理论依据。
[1] 李宪华, 郭永存, 张军, 郭帅. 模块化六自由度机械臂逆运动学解算与验证[J]. 农业机械学报, 2013, 44(4): 246-250.
[2] 刘金存, 鲁守银, 姜振廷, 刘珍娜, 黄晓萍. 一种液压机械臂逆运动学求解新算法[J]. 制造业自动化, 2013, 35(6): 39-42.
[3] 张金涛, 徐文福, 孟得山. 基于臂型角参数化的冗余空间机械臂逆运动学求解方法[C]. 西安: 第32届中国控制大会, 2013.
[4] Pieper D L. The kinematics of manipulators under computercontrol[D]. California: Stanford University, 1968.
[5] Duffy J. Analysis of mechanisms and robot manipulators[M]. London: Edward Arnold, 1980.
[6] 王俊龙, 张国良, 敬斌, 徐君. 一种新的六自由度机械臂运动学反解方法研究[J]. 计算机工程与应用, 2013, 49(22): 266-270.
[7] 姜宏超, 刘士荣, 张波涛. 六自由度模块化机械臂的逆运动学分析[J]. 浙江大学学报, 2010, 44(7): 1348-1354.
[8] 朱静芬, 韩丹夫. “牛顿类”迭代的收敛性和误差估计[J]. 浙江大学学报(理学版), 2005, 32(6): 623-626.
[9] 尹钊, 贾尚晖. Moore-Penrose广义逆矩阵与线性方程组的解[J]. 数学的实践与认识, 2009, 39(9): 239-244.
[10] 王莎莎. 广义逆矩阵的性质及应用[J]. 才智, 2014(19): 149.
Inverse Kinematical Numerical Method Based on6-DOF Space Manipulator
Zhang Xu-man, Zhang Zhong-zhe, Wang Yan-bo, Yang Tao, Deng Tao
(Beijing Institute of Precision Mechanical and Electrical Control Equipment, Beijing, 100076)
Analytical method is only applicable to the manipulators with special structure and the solving process is complicated with a large amount of calculation. Aiming at this problem, a kind of inverse kinematical iterative method is proposed for most serial manipulators. This method is used to obtain the inverse kinematics solution of a 6-DOF space manipulator which is independently researched and developed. Then the reliability of this method is proved through the simulation.
Space manipulator; Numeric iteration; Forward kinematics and inverse kinematics
1004-7182(2016)03-0081-04
10.7654/j.issn.1004-7182.20160319
V476
A
2015-03-15;
2015-05-10
张栩曼(1990-),女,助理工程师,主要研究方向为空间机器人
