CSP生产模式下轧制计划编制模型及算法
2016-06-04张启敏唐秋华毛永年王春锋
张启敏,唐秋华,郑 鹏,毛永年,王春锋
(1.武汉科技大学机械自动化学院,湖北 武汉,430081; 2.武汉钢铁股份有限公司条材总厂,湖北 武汉,430083)
CSP生产模式下轧制计划编制模型及算法
张启敏1,2,唐秋华1,郑鹏1,毛永年1,王春锋2
(1.武汉科技大学机械自动化学院,湖北 武汉,430081; 2.武汉钢铁股份有限公司条材总厂,湖北 武汉,430083)
摘要:针对紧凑式带钢生产(CSP)模式下的轧制计划编制问题,综合考虑设备能力、订单需求和相邻板坯间厚度跳跃,提出一种两阶段问题求解框架。第一阶段以最小化轧制单元数和非计划卷使用量为目标建立整数规划模型,为保证模型的求解效率,从生产实际中提炼出“优先薄板,后补非计划材”的启发式规则进行求解。第二阶段以最小化板坯间平均厚度跳跃为目标来建模,综合考虑非计划卷厚度可变的特性,提出一种多邻域结构的变邻域搜索算法进行求解。通过某CSP生产线的轧制计划编制实例验证了该模型和算法的有效性。
关键词:连铸连轧;轧制计划;CSP;启发式规则;变邻域搜索
紧凑式带钢生产(compact strip production, CSP)是薄板坯连铸连轧技术框架下的一种典型生产模式。CSP生产模式下,铸机生成的板坯通过均热炉缓冲后直接进入轧机轧制,而合理的轧制计划是协调连铸连轧生产节奏、保证CSP生产顺行的关键。
针对热轧轧制计划编制问题的研究成果有很多。Tang等[1]建立了轧制计划编制问题的多旅行商模型,通过改进遗传算法对模型进行求解,以并行策略同时编制多个轧制单元方案。贾树晋等[2]以最小化相邻板坯参数跳跃惩罚和最大化轧制计划内板坯数为目标,建立了基于奖金收集车辆路径问题的多目标优化模型,采用蚁群算法按并行策略进行求解。董广静等[3]建立以最小化轧制计划内钢坯出库总倒垛次数与轧制单元之间切换机架次数为目标的多目标整数规划模型,并通过一种单亲遗传算法进行求解。邹宗华等[4]以旅行商模型为基础,针对两台连铸机对一台轧机的CSP生产模式进行建模,提出了基于人机交互技术和最近插入法的实用解法。
以上方法针对具体的轧制计划编制问题都体现出较好的求解性能,但需要注意的是,这几种求解方法在对目标函数进行处理时,都以板坯间宽度、厚度、强度等参数的跳跃惩罚函数表为基础,以板坯间的总跳跃罚值作为考量指标。由于跳跃惩罚函数表由工艺员根据经验来制定,因此在很大程度上降低了这些求解方法的科学性和所得结果的较优性。本文以订单和设备能力为导向,通过确定不同厚度范围内板坯的安全过渡值,首先根据“优先薄板,后补非计划材”的启发式规则确定所需轧制单元数量、组合形式以及所需非计划卷数量,再利用变邻域搜索算法确定非计划材的厚度以及每个轧制单元内板坯的排序,最后通过实际案例对算法的性能进行验证。
1CSP轧制计划编制问题
1.1问题描述
轧制计划编制涉及从连铸到轧制这一连续生产过程,图1所示为某钢厂由两台铸机、两台均热炉和一台轧机构成的CSP生产线,其中两台均热炉以交替摆动的形式为轧机供钢。在轧制环节,用,它有且只有一种轧制组合形每当轧制若干块板坯后需要更换轧辊,且每次更换的新轧辊都需要先轧制特定厚度的板坯进行预热。一个换辊周期内轧制的板坯被称为一个轧制单元,每个轧制单元包含不同厚度的板坯,且板坯需按照一定的规则排序。
轧制计划编制的任务就是将不同规格的订单编制成若干轧制单元,通常需要考虑的目标包括:①为保证钢卷质量同时提高轧辊使用寿命,编制轧制单元时,相邻两块板坯的厚度不能跳跃太大,且应尽量避免板坯间从薄到厚的“反向跳跃”;②为保证轧制单元内板坯参数的平缓过渡,在缺少某种规格的订单时,需加入一些“无主”的板坯作为“过渡材”。由于这些板坯生产后没有订单需求,因此在编制轧制计划时应保证这样的“非计划卷”最少;③在不超过最大能力范围的条件下,应尽量提高轧辊的利用率,进而减少换辊次数。

图1 CSP工艺流程示意图
Fig.1 Schematic diagram of CSP process
1.2两阶段求解框架
现有对轧制计划编制的研究,通常都是先制定不同厚度的跳跃惩罚函数表,再以最小化总跳跃惩罚为目标,以保证所编制方案内板坯间的平稳过渡。近年来,随着国家钢铁产业的不断转型升级,薄规格、高强度、复杂成分钢等高附加值钢材逐渐成为主导产品[5]。在板坯整体厚度差别较小但对钢卷表面质量要求更高的情况下,仅以人为制定的惩罚函数来编制轧制计划变得较为困难。与此同时,由于订单中薄板坯钢卷所占比重较大,在现阶段部分CSP生产线的实际生产中,轧制单元内板坯厚度变化并不完全服从传统的U形或者碗状曲线,而是在烫辊过渡之后尽可能多轧主体材薄板。
根据对轧机能力历史数据的分析,可以确定在一个换辊周期内轧辊对不同厚度范围板坯的安全过渡量,即至少轧制多少某一厚度范围的板坯之后才能安全过渡到下一个较薄的厚度范围区间。但由于不同钢种的成分不同,导致其硬度指标也不相同,因而轧机针对不同钢种板坯的厚度过渡要求各异。以DC01级别钢为例(见表1),表1中安全过渡量为较厚板坯在该区间的最少轧制量,实际编排时可大于该值。一个轧制单元的最大轧制板坯重量为1000 t,开轧厚度为3.0 mm,至少轧制120 t厚度为2.0~3.0 mm的板坯之后才能开始轧制1.6~2.0 mm厚度的板坯,以此类推。对每个轧制单元来说,从最厚板坯到最薄板坯的过程中,厚度范围间不能出现跳跃。从而可以推算出,在实际生产组织时,每个轧制单元只可能采用表1中五种可能组合中的一种。针对其它级别的钢种,同样可以得到类似的安全过渡量及组合形式,但不同钢种的厚度范围及过渡值不同。

表1 DC01钢的轧辊安全过渡量及轧制单元组合形式
在轧制薄板时,由于设备能力要求必须采用厚板进行过渡,如果在订单中未含有该厚度范围的板坯或者其数量不足,则需要添加非计划卷作为过渡材。考虑到在实际生产时,若将薄板排在多个轧制单元内,势必需要更多过渡材。为此,本文提出一种考虑设备能力、订单需求和板坯厚度跳跃的两阶段求解框架。首先按照从薄到厚的顺序将订单内的板坯排入轧制单元,最小化轧制单元个数和过渡材使用量,确定该轧制单元所采用的组合形式。然后对所有轧制单元内的板坯进行排序,以最小化平均厚度跳跃为优化目标,保证板坯间的平缓过渡。
2考虑设备能力和订单需求的轧制计划编组
该问题可描述为:假定所有板坯的集合为I,每块板坯的编号为i(i∈I),且其中部分来自订单需求Ip,另一部分为非计划卷Im(Im=IIp)。每块板坯重量为w,厚度为Hi,若该板坯的厚度在厚度范围u之内,则Miu=1,否则为0。根据轧制工艺要求设置板坯厚度范围,对于DC01钢,u=1、2、…、5,分别对应表1中的板坯厚度类型A、B、…、E。用c表示轧制单元组合形式,对于DC01钢,c=1、2、…、5,分别对应表1中的轧制单元组合I、II、…、V,且知该组合形式下第u厚度范围的重量阈值为Dcu。要求在完成全部订单的前提下,最小化所使用的轧制单元数,最小化所使用的非计划材数量,同时确认每个轧制单元所采用的组合形式。为此,还定义了三个0-1决策变量Xir、Yrc和Zr。若板坯i属于轧制单元r,则Xir取1,否则为0;若轧制单元r采用组合c进行生产,则Yrc取1,否则为0;若轧制单元r被使用,则Zr取1,否则为0。
目标函数:
(1)
(2)
其中:式(1)为最小化使用的轧制单元数量;式(2)为最小化非计划卷数量。
面向订单及库存的约束:
(3)
(4)
其中:式(3)表示来自于订单的任一板坯i都必须且只能分到某一个轧制单元;式(4)表示非计划板坯非必须完成。
轧制单元启用约束:
(5)
(6)
式中:MAX为一个极大的正数;R为轧制单元总数。式(5)表示对于任意的一个轧制单元r,若未被使用,则不可以为其分配板坯;式(6)表示在轧制单元分配时,需要按照从前往后的顺序依次使用。
轧制组合约束:
(7)
式(7)表示若轧制单元r被启用,它有且只有一种轧制组合形式。
轧制单元内约束:
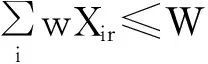
(8)
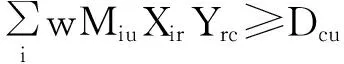
(9)

(10)
其中:式(8)表示每一个轧制单元r的重量小于设定值W;式(9)表示在每一个轧制单元r内,除最薄厚度范围Uc外,其余各厚度范围的板坯重量须大于设定值Dcu;式(10)表示在最薄厚度范围Uc内的板坯重量必须小于设定值Dcu。
联立式(1)~式(10)就形成轧制计划编组的数学模型。分析该模型可知,由于存在三种二元决策变量,采用分支定界方法即可求解。然而,现场每日调度的板坯数量较多,源于订单的板坯加上各类非计划卷,其总量超过100块。由于运算规模较大,采用分支定界方法难以满足现场调度的实时性需求。为加快运算速度,本文提出一种启发式规则,该规则基于“优先薄板,后补非计划材”的思想,其具体操作步骤是:
(1) 先将现有订单内最薄厚度范围的板坯编入一个轧制单元,直至达到其最大安全过渡量。
(2) 优先使用订单内的板坯作为这些薄板的过渡材;如不能满足安全过渡量要求,则添加相应的非计划卷作为过渡。
(3) 在最薄厚度范围内的板坯编制完毕后,以同样的方法编制次薄厚度的板坯,直到所有订单板坯编制完毕,汇总所有非计划卷量及其厚度范围。
在这种规则下,薄板均以最小的过渡材代价进行轧制,同时可以确定各轧制单元内各厚度范围板坯的个数。
3考虑平均厚度跳跃的板坯排序
通过第一阶段的求解,多块处于同一个厚度范围的板坯可能被分到同一个轧制单元,呈现出极大的厚度跳跃。从工艺角度分析,这不利于设备状态维护,也不利于稳定产品质量。为此,将第一阶段决策中同一厚度范围内的全部板坯集中,重新进行排序,旨在降低相邻板坯间的厚度跳跃,实现稳定生产。

目标函数:
(11)
式中:Diffrt为轧制单元内发生板坯间厚度跳跃的次数。式(11)表示最小化板坯间平均厚度跳跃值。
轧制单元内约束:
(12)
式(12)定义各轧制厚度范围内板坯总数为第一阶段所求值。
板坯约束:
(13)
式(13)表示各轧制厚度范围内的每一块板坯都需要被分配一次。
事件点约束:
(14)
(15)
式(14)、式(15)表示在每个轧制单元内,当前板坯t前面的事件点上,最多只有一块板坯,而其后面的事件点上没有板坯。
同一轧制单元内厚度约束:
∀t (16) 式(16)表示在同一个轧制单元内,板坯厚度必须从厚到薄变化。 跳跃判定: (17) 式(17)为对同一个轧制单元内相邻板坯间厚度跳跃次数Diffrt的约束。 联立式(11)~式(17)构造板坯排序模型。该模型中的变量都是整数,可用整数规划方法求解。这种处理模式下的排序操作类似于一个具有多约束的装箱问题,为此设计了一种变邻域搜索算法进行求解。变邻域搜索(variable neighborhood search, VNS)算法[6]是一种有效的局部搜索算法。该算法在局部搜索范围内,通过系统化地改变多个邻域结构,有效拓展搜索空间,从而跳出局部最优解,迅速逼近全局近似最优解。 初始化:为保证初始解的性能,针对某个厚度范围进行排序时,先将符合该厚度范围的订单板坯按照从厚到薄的顺序排序,再按次序将其轮流放入各轧制单元内,如图2所示。 邻域结构:根据具体问题特性,设计了交换、互通、插入三种基本邻域结构,分别如图3(a)、图3(b)、图3(c)所示。除此之外,考虑到添加的非计划卷厚度不定的特点,设计了一种改变非计划卷厚度的特殊邻域结构,如图3(d)所示(图中斜线为非计划卷)。 评价函数:将板坯间的平均厚度跳跃值(即总跳跃量除以发生跳跃的次数)作为评价函数,目标为令其最小化。例如,有相邻4块板坯厚度分别为3.0、2.5、2.5、2.0 mm,总跳跃量为1.0 mm,在3.0~2.5 mm和2.5~2.0 mm处共出现两次跳跃,平均厚度跳跃值即为1.0/2=0.5 mm。 Fig.2 Initialization method 图2 初始化方法 在进行变邻域搜索时,首先生成初始化解,再对其依次进行4种邻域结构的邻域搜索,设定每种邻域结构搜索500次,全部搜索完毕后算法结束。整个算法流程的伪代码如图4所示。 图3 邻域结构 4实例分析 采用本文提出的算法对某钢厂CSP生产线进行轧制计划编制,分别选取了DC01、Q215B、SPA-H三个钢种进行求解,表2为各算例的统计结果,表中“人工解”为现场调度员根据经验制定的轧制计划。在现场调度时,为方便操作,通常以“贪心”规则进行板坯编组:首先将有订单需求的板坯安排进当前轧制单元,优先保证当前轧制单元的规格跳跃,以此类推依次将所有订单内板坯进行编制,编制过程中按照需要添加相应厚度的非计划卷。 图4 变邻域搜索算法伪代码 算例板坯数/块钢种轧制单元数/个人工解优化解均值 实际使用板坯数/块人工解优化解均值 平均厚度跳跃/mm人工解优化解均值1240DC01982942580.200.172240Q215B882622590.180.183240SPA-H882582480.170.164300DC0112113453280.180.165300Q215B11113253150.190.176300SPA-H12123553440.180.177360DC0113124223930.210.178360Q215B13124194070.160.169360SPA-H12123883770.170.16 从表2可以看出,针对不同规模的算例,本文算法相较于人工编制方法在各个指标上都有不同程度的改进,由于各算例的订单板坯厚度不同,故优化程度也各异。总体来看,与人工调度相比,采用本文算法进行优化后,在4个算例中减少了一个轧制单元使用量,实际使用板坯数平均降低了约5%,板坯厚度跳跃平均降低了约8%。 为进一步验证算法的实际优化效果,对其中的一个算例进行了具体分析。表3为算例1中DC01板坯的订单厚度规格,算例中每个轧制单元的总轧制量不超过1000 t,考虑到运输的便利,板坯的单位重量为30 t,各厚度板坯的安全过渡量可参见表1。 基于文中提出的两阶段模型,针对小规模问题直接采用GAMS/Cplex软件即可求解。本例中共240块订单板坯,约为一条双流CSP生产线两天的轧制任务,规模较大,故而采用所提出的启发式算法求解,生成的轧制计划如表4所示。 表3 DC01板坯规格 表4 DC01轧制计划 从表4可看出,由于本例订单中薄板数量较多,人工调度在进行轧制计划编制时按“贪心”规则选择当前最优解,在编制前几个轧制单元时可保证较好的结果,但对之后的轧制单元编制效果不佳,导致需要较多的非计划卷作为过渡材。而本文算法对所有轧制单元进行全局优化,有效地保证了轧制计划的总体优越性,同时使各轧制单元间保持了性能的相对稳定。 5结语 在当前钢铁市场上高强度、薄规格轧钢产品占订单主体的形势下,本文以订单和设备能力为导向,提出了CSP生产模式下的两阶段轧制计划编制方法。通过对设备能力的统计分析,以最小化轧制单元数和非计划卷数量为目标,保证了订单兑现前提下的利润最大化。以并行策略进行的板坯间排序,有效保证了多个轧制单元板坯间厚度的均匀跳跃,可提高轧辊的使用寿命,同时保证了钢卷的表面质量。 参考文献 [1]Tang Lixin, Liu Jiyin, Rong Aiying, et al. A multiple traveling salesman problem model for hot rolling scheduling in Shanghai Baoshan Iron & Steel Complex[J]. European Journal of Operational Research,2000,124:267-282. [2]贾树晋,李维刚,杜斌.热轧轧制计划的多目标优化模型及算法[J].武汉科技大学学报,2015,38(1):16-22. [3]董广静,李铁克,王柏琳,等. 考虑倒垛因素的轧制计划编制方法[J]. 控制与决策, 2015,30(1):149-155. [4]邹宗华,李铁克. CSP生产线轧制计划模型及算法[J]. 冶金自动化,2003,27(2):18-22. [5]毛新平,高吉祥,柴毅忠.中国薄板坯连铸连轧技术的发展[J].钢铁,2014(7):49-60. [责任编辑尚晶] Model and algorithm for rolling scheduling of compact strip production ZhangQimin1,2,TangQiuhua1,ZhengPeng1,MaoYongnian1,WangChunfeng2 (1.College of Machinery and Automation, Wuhan University of Science and Technology, Wuhan 430081, China;2.General Rod Product Plant,Wuhan Iron and Steel Co.,Ltd., Wuhan 430083,China) Abstract:Aiming at the rolling scheduling problem in a compact strip production (CSP) plant, this paper provides a two-stage solution framework which takes into account the equipment capacity, the order requirement and the thickness variation between adjacent slabs. In the first stage, an integer programming model is proposed to minimize the numbers of rolling units and unplanned slabs simultaneously. To solve this model efficiently, a heuristic rule extracted from the production practice is employed so that thinner slab is entitled with higher priority and unplanned slab will be manufactured unless it is quite necessary. The model of the second stage is built to lower the thickness variation between adjacent slabs and is solved by a variable neighborhood search algorithm which considers the variable thickness values of unplanned slabs. Examples of rolling scheduling in a CSP plant testify the effectiveness of the proposed model and algorithm. Key words:continuous casting and rolling; rolling schedule; CSP; heuristic rule; variable neighborhood search 收稿日期:2015-11-13 基金项目:国家自然科学基金资助项目(51275366,51305311);高等学校博士学科点专项科研基金课题(博导类,20134219110002);中国博士后科学基金资助项目(2013M542073). 作者简介:张启敏(1967-),男,武汉科技大学博士生.E-mail:37977559@qq.com 通讯作者:唐秋华(1970-),女,武汉科技大学教授,博士生导师.E-mail:tangqiuhua@wust.edu.cn 中图分类号:TG334. 9 文献标志码:A 文章编号:1674-3644(2016)01-0024-06





