新型完全各向同性3T并联机构及其特性分析

曹浩峰　曹　毅, 2　秦友蕾　丁　锐

1.江南大学江苏省食品先进制造装备技术重点实验室，无锡，2141222.上海交通大学机械系统与振动国家重点实验室，上海，200240



新型完全各向同性3T并联机构及其特性分析

曹浩峰1曹毅1, 2秦友蕾1丁锐1

1.江南大学江苏省食品先进制造装备技术重点实验室，无锡，2141222.上海交通大学机械系统与振动国家重点实验室，上海，200240

摘要：针对并联机构耦合带来运动学分析与控制困难的问题，提出了一种新型完全各向同性的三维移动并联机构，该并联机构动平台和静平台之间由3条支链连接，3条支链的第一个移动副在空间中呈正交分布，使得该机构的动平台具有3个移动自由度，且输入输出一一对应。这种机构最突出的优点是运动副简单，三维移动解耦，运动学分析简单，便于该机构运动控制设计。采用螺旋理论分析了该机构的自由度及性质，确定了机构的主动副，给出了机构的位置和速度正反解，分析了机构工作空间及运动性能。根据机构输入输出关系，求得机构雅可比矩阵，验证了机构具有完全各向同性。研究结果对该机构的进一步应用具有理论指导意义。

关键词：并联机构；运动学；工作空间；各向同性

0引言

由于并联机器人相对串联机器人具有一些独特的性能，如刚度大、承载能力强、无累积误差、自重负荷比小、动力性能好等，所以引起人们长期的关注，很多学者进行了大量的研究。相对于六自由度并联机构，少自由度并联机构因具有驱动元件少、结构紧凑而具有较高的实用价值，同时机构造价低，控制容易，在工业生产及其他领域有着广阔的应用前景。

强耦合性是一般并联机构的共同特性。并联机构的强耦合性指机构动平台的一个输出运动由若干个主动输入联合控制[1]。并联机构的强耦合性使其具有刚度好、承载能力强的优点，但同时也有运动学求解复杂、控制设计困难等弱点。因此，在承载能力要求不高的应用领域，可以选用解耦并联机构。目前，国内外学者对解耦并联机构的设计和分析已经做了大量工作[2-5]。

对于解耦的并联机构，其理论分析和实体研制将更简便，控制与轨迹规划得到简化，故解耦并联机构已成为当前机构学领域的研究热点之一[6]。Li等[4]提出了仅由转动副组成的R-CUBE三自由度移动解耦并联机构；金琼等[7-8]分析了一类新型三平移解耦并联机构；Glazunov[9]运用螺旋理论设计了解耦的并联机构。目前，对解耦并联机构的研究还未形成系统化的理论，没有一套普适的方法来判别和设计解耦并联机构[10]。

本文提出的三自由度并联机构能够实现运动平台的三维移动。该机构由3条正交分布的支链把动平台和静平台连接起来，机构在空间三维移动方向解耦。与DELTA机器人相比，此机构运动学正逆解简单，工作空间大，结构和控制简单，具有良好的应用前景。本文首先运用螺旋理论分析机构原理及自由度，确定机构的主动副和消极副，然后对其进行运动学分析、解耦性分析、工作空间分析，最后给出机构的运动性能指标，验证机构具有完全各向同性。

1三平移并联机构特性分析

1.12-PRRPR/PRRPR并联机构结构介绍

2-PRRPR/PRRPR并联机构由3条支链将动平台和静平台相连。每条PRRPR分支都具有5个自由度。将每个分支的每个运动副进行编号，可以表示成第i条支链的第j个运动副。其中，第一条支链和第三条支链完全相同，第一个移动副Pi1平行于第二个转动副Ri2和第三个转动副Ri3的轴线，第四个移动副Pi4与第五个转动副Ri5的轴线平行，并且Pi1和Pi4相互垂直(i=1,3)。对于第二条支链，第一个移动副P21平行于第二个转动副R22和第三个转动副R23的轴线，第四个移动副P24与第五个转动副R25的轴线及P21相互垂直。

3条支链的第一个移动副在空间中呈正交放置，按照图1所示建立空间直角坐标系，则P11平行于Z轴，P21平行于X轴，P31平行于Y轴。

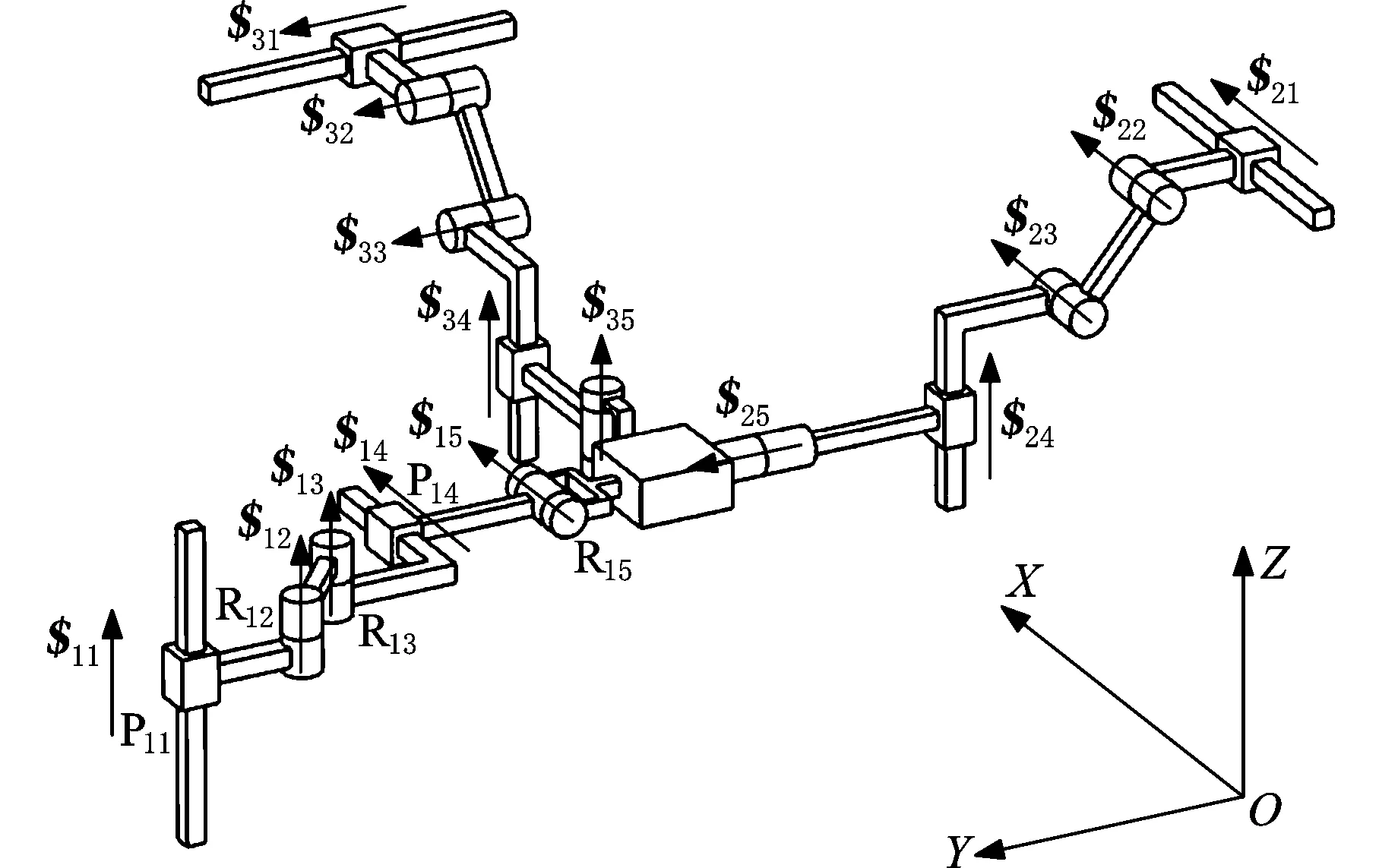
图1　2-PRRPR/PRRPR并联机构

机构的自由度分析是机构分析的基础。少自由度并联机构由于受到各支链施加于动平台上约束的合成作用而导致自由度减少。

修正的Grübler-Kutzbach通用自由度计算公式为：

(1)

式中，M为机构的自由度；d为机构的阶数，它依赖于公共约束，d=6-λ；λ为公共约束；n为包括机架的构件数目；g为运动副的数目；fi为第i个运动副的自由度；μ为机构中过约束的总数；ζ为机构中存在的局部自由度。

如图1所示,整个机构由14个构件(每条支链有4个构件，另有1个动平台，1个静平台，所以构件总数n=14)组成。每条支链PRRPR都有5个运动副，所以运动副总数g=15。机构不存在过约束、局部自由度和公共约束，所以μ=ζ=0，d=6。这样,机构的自由度为

M=6×(14-15-1)+15=3

(2)

1.2基于螺旋理论的自由度分析

螺旋在机构运动学研究中起着重要作用，它由一组空间的对偶矢量构成，在几何学上可以同时表示直线在空间的方向和位置。刚体的运动可以通过绕某一直线的转动加上沿平行于该直线的移动得到,这种运动称之为螺旋运动。作用在刚体上的任何力系可以合成为一个作用于某直线的集中力和绕该直线的力矩,这种力和力矩称为力螺旋,它与运动螺旋存在对偶关系[11]。

空间任何一条直线可以用一个螺旋来表示：

$=(S;S0)

(3)

式中，S为螺旋轴线方向的单位矢量；S0表示对偶矢量。

螺旋在Plüker坐标下表示为(lmn；pqr)，可表示刚体的一般运动以及刚体上的作用力。

若$∘$r=0则两旋量互易积为零，称这两个螺旋互逆。螺旋$r为$的反螺旋。

根据反螺旋理论可知，当$1，$2，…，$n表示并联机构支链上的运动螺旋系时，其反螺旋$r就表示该支链运动螺旋系施加给动平台的约束螺旋,即支链对动平台的约束力和力偶。机构末端约束螺旋系为所有支链约束螺旋组成的螺旋系。机构末端约束螺旋系决定机构的自由度，其最大线性无关数就等于机构被约束的自由度数。而所有支链都有的相同约束反螺旋即为公共约束。

图1所示为并联机构的螺旋系，用$ij表示第i条支链的第j个运动副的运动螺旋。lij、mij、nij、pij、qij、rij表示第i条支链的第j个运动副的运动螺旋Plüker坐标。

为分析机构性质，选取第一条支链，其5个运动螺旋可表示为

$11=(0 0 0;0 0 1)

$12=(0 0 1;p12q120)

$13=(0 0 1;p13q130)

$14=(0 0 0;1 0 0)

$15=(1 0 0;0q15r15)

基于螺旋互易积为零的原理可求解第一支链分支螺旋系的反螺旋：

(4)

式(4)表明，第一支链分支螺旋系的反螺旋是一个节距为无穷大的约束力偶，它限制了机构沿Y轴的转动自由度。

第二条支链的运动螺旋系为

$21=(0 0 0;1 0 0)

$22=(1 0 0;0q22r22)

$23=(1 0 0;0q23r23)

$24=(0 0 0;0 0 1)

$25=(0 1 0;p250r25)

同理可得第二支链的反螺旋为

(5)

由式(5)可知，第二支链分支螺旋系的反螺旋是一个节距为无穷大的约束力偶，它限制了机构沿Z轴的转动自由度。

第三条支链的运动螺旋系为

$31=(0 0 0;0 1 0)

$32=(0 1 0;p320r32)

$33=(0 1 0;p330r33)

$34=(0 0 0;0 0 1)

$35=(0 0 1;p35q350)

同理可得第三支链的反螺旋为

(6)

由式(6)可知，第三支链分支螺旋系的反螺旋是一个节距为无穷大的约束力偶，它限制了机构沿X轴的转动自由度。

上述研究表明，3条支链产生3个作用到动平台上的约束力偶且这三个力偶彼此线性无关，它们约束了动平台上的3个转动自由度，所以此并联机构具有空间三维移动自由度。

2并联机构驱动选取及消极副的判定

2.1机构主动副的选取

可采用基于螺旋理论的并联机构驱动选取方法来选取机构主动副。该方法为：锁定选定的驱动，如果驱动选取正确，则当驱动被限制住的时候，动平台将失去全部的自由度，所以动平台的约束螺旋系的最大线性无关数为6[12]。

在自由度分析中可知，此机构具有三维移动的自由度，所以此机构必须有3个主动副。根据主动副选取原则[13]，选取与定平台相连的3个在空间相互垂直的移动副为驱动。此时，刚化这3个移动副后，对每条支链分别求取其运动螺旋的反螺旋，可得到动平台的约束螺旋系为

(7)

显然,式(7)中的6个约束螺旋系线性无关，所以,此时的动平台自由度为0，即当3个移动副被刚化后,动平台不能运动，所以驱动选取正确。

2.2机构消极副的判定

记动平台的角速度矢量为ωn，固定在动平台上的参考坐标系原点线速度矢量为vn，则动平台的运动螺旋为

(8)

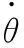
对于支链1，将运动螺旋系代入(8)中，可得

(9)

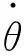
由此可以看出，支链1的第五个转动副R15的转动速度为0，即此转动副为消极副，它在机构中的作用只是增加灵巧性。同理可得支链2和支链3的第五个转动副R25和R35的转动速度为0。

因此，此并联机构各支链的第五个转动副在机构发生运动时均不发生转动，是个消极的运动副。并联机构可以简化为完全对称的3-PRRP机构，这样可以简化后续的运动学分析。

3并联机构运动学分析

3.1位置分析

如图2所示，将固定坐标系OXYZ设定在机架的右下方,动坐标系pxyz设置在动平台的几何中心上。支链1中P11的起始点位于XY平面，距X轴D1x，距Y轴D1y，P11的输入位移为q11。支链2中P21位于XZ平面，它的起始点距X轴D2x，距Z轴D2z，P21的输入位移为q21。支链3中P31的起始点距YZ平面D3x，距XZ平面D3y，距XY平面D3z，P31的输入位移为q31。第一个移动副的行程为L1，它距离第二个转动副的距离为a，第二个转动副与第三个转动副的距离为L2，第三个转动副距离第四个移动副的起始端的距离为b，第四个移动副的行程为L3，第四个移动副距离动平台中心点的距离为c。3条支链中，第二个转动副与第三个转动副的连线的转动角度分别为ɑ1、β1、γ1。

图2　并联机构运动参数示意图

根据图2所示的几何关系，可得动平台中心点p的位置坐标：

对于第一条支链，p的位置坐标为

(D1y+L2cosα1+q12，D1x-a-L2sinα1-b-c，q11)

对于第二条支链，p的位置坐标为

(D2y+q21，a+L2sinβ1+b+c，D2x-L2cosβ1-q22)

对于第三条支链，p的位置坐标为

(D3x-a-L2sinγ1-b-c，D3y+q31，D3z-L2cosγ1-q32)

即

px=D1y+L2cosα1+q12=D2y+q21=

D3x-a-L2sinγ1-b-c

py=D1x-a-L2sinα1-b-c=

a+L2sinβ1+b+c=D3y+q31

pz=q11=D2x-L2cosβ1-q22=D3z-L2cosγ1-q32

由此可以得到此并联机构的运动学正解为

(10)

由式(10)可以得到运动学的逆解为

3.2速度与加速度分析

可以用雅可比矩阵来表达并联机构动平台的输出速度和驱动关节的输入速度之间的映射关系，即

将式(10)左右两边同时对时间求一阶导数得机构输入速度与动平台输出速度间的关系为

则机构输出速度与驱动之间的关系写成矩阵形式为

并联机构的雅可比矩阵为

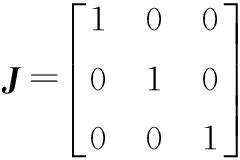
将式(10)左右两边同时对时间求二阶导数得机构输入与动平台输出之间加速度关系为

3.3工作空间分析

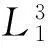
给定并联机构尺寸参数，令L1=10 cm，D2y=15 cm，D2x=10 cm，则此时的工作空间如图3所示。

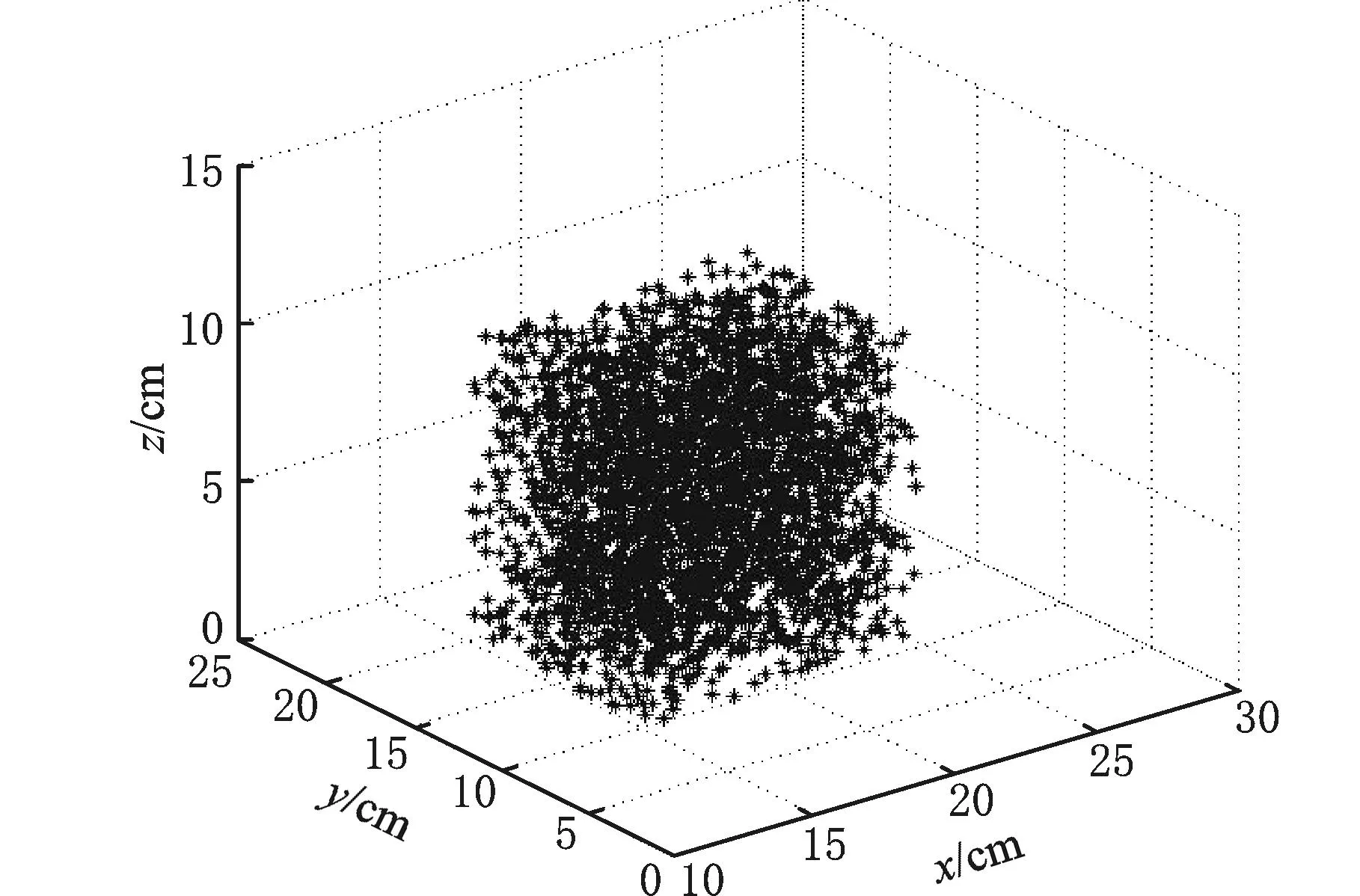
图3　并联机构工作空间

4机构运动性能指标研究

4.1奇异性

根据雅可比矩阵的表达形式，并联机构可以分为以下4种类型[14]：①若J是对角阵且对角线上的元素都相同，则机构具有完全各向同性;②若J为对角阵，但对角线上的元素并不全部相同，则并联机构完全解耦；③若J是三角阵，则机构部分解耦；④若J既不是对角阵，又不是三角阵，则机构为耦合并联机构。此机构的雅可比矩阵为对角阵且对角阵上的元素均为1，所以此机构具有完全各向同性。

机器人的雅可比矩阵依赖于其关节位形。奇异位形是指雅可比矩阵的秩比任务空间维数小时的位形，是机器人机构固有的运动学特性。此机构的雅可比矩阵的秩等于任务空间维数，机构不具有奇异位形。

4.2条件数

雅可比条件数k(J)可以用来描述机器人的灵活性[15]。根据矩阵理论可知，雅可比矩阵的条件数定义为

‖J‖为矩阵J的范数，通常取欧氏范数，即

其中j1、j2、…、jn是矩阵J的各个列矢量。

由数学知识得条件数k(J)变化范围为[1，∞)，k越接近1，雅可比矩阵的性态越好，k越大，雅可比矩阵越趋于病态。所以，在进行机器人机构设计时，要使机构的雅可比矩阵尽可能各向同性，也就是控制雅可比矩阵的条件数接近1。k=1时，机器人处于各向同性，所具有的位形各向同性，雅可比矩阵的奇异值相等，此时机器人灵活性最高。可以证明，雅可比矩阵条件数是其最大奇异值与最小奇异值之比，即

k(J)=σ1/σm

此机构的雅可比矩阵J恒为3×3的单位阵，其σ1=σm=1。则条件数k(J)=1，说明机构具有完全各向同性。

5结论

(1)2-PRRPR/PRRPR机构具有3条支链，每条支链中的第一个移动副在空间中呈正交分布。选用第一个移动副作为驱动副，机构属于非过约束机构，每条支链的第五个转动副为消极副，其作用仅为消除过约束，在机构运动过程中不发生连续转动，对动平台的运动没有影响。通过简化机构方便了后续的运动学分析。

(2)推导了机构的正反解、速度和加速度，验证了机构的运动解耦特性，输入、输出为一一对应，即机构的运动完全解耦，便于并联机构的实时控制和轨迹规划，弥补了现有的三自由度平动并联机器人运动耦合的缺陷。机器人的驱动副均为移动副，因此承载能力较大，适用范围较广，具有较好的应用前景。

(3)机构位置工作空间大，速度雅可比矩阵为3×3阶单位阵，具有完全各向同性，不存在运动学奇异，条件数为1，具有很好的运动学性能和灵活性。研究结果对三维移动完全各向同性并联机构的进一步应用具有一定的理论指导意义。

参考文献：

[1]张彦斌, 吴鑫. 完全解耦二移动二转动并联机构结构综合[J]. 农业机械学报, 2013, 44(8):250-256.

ZhangYanbin,WuXin.StructuralSynthesisofFully-decoupledTwo-translationalandTwo-rotationalParallelMechanisms[J].TransactionsoftheChineseSocietyforAgriculturalMachinery, 2013, 44(8):250-256.

[2]GoguG.Fully-isotropicParallelRobotswithFourDegreesofFreedomT2R2-type[C]// 2005IEEE/RSJInternationalConferenceonIntelligentRobotsandSystems, 2005(IROS2005).Edmonton:IEEE, 2005:960-965.

[3]RichardPL,GosselinCM,KongX.KinematicAnalysisandPrototypingofaPartiallyDecoupled4-DoF3T1RParallelManipulator[J].JournalofMechanicalDesign, 2007, 129(6): 611-616.

[4]LiW,GaoF,ZhangJ.R-CUBE,aDecoupledParallelManipulatorOnlywithRevoluteJoints[J].MechanismandMachineTheory, 2005, 40(4): 467-473.

[5]LegnaniG,FassiI,GibertiH,etal.ANewIsotropicandDecoupled6-DoFParallelManipulator[J].MechanismandMachineTheory, 2012, 58: 64-81.

[6]侯雨雷, 张占叶, 胡鑫喆, 等. 新型两转动自由度完全解耦并联机构及其特性[J]. 哈尔滨工业大学学报, 2014, 46(9):80-85.

HouYulei,ZhangZhanye,HuXinzhe,etal.ANovel2-DOFFullyDecoupledRotationalParallelMechanismandItsCharacteristics[J].JournalofHarbinInstituteofTechnology, 2014, 46(9):80-85.

[7]金琼, 杨廷力. 一类新型三平移并联机器人机构的位置分析[J]. 东南大学学报: 自然科学版, 2001, 31(5): 33-38.

JinQiong，YangTingli.PositionAnalysisforaClassofNovel3-DOFTranslationalParallelRobotMechanisms[J].JournalofSoutheastUniversity(NaturalScienceEdition), 2001, 31(5): 33-38.

[8]JinQ,YangTL.SynthesisandAnalysisofaGroupof3-degree-of-freedomPartiallyDecoupled

ParallelManipulators[J].JournalofMechanicalDesign, 2004, 126(2): 301-306.

[9]GlazunovV.DesignofDecoupledParallelManipulatorsbyMeansoftheTheoryofScrews[J].MechanismandMachineTheory, 2010, 45(2): 239-250.

[10]杭鲁滨, 王彦, 吴俊, 等. 基于拓扑解耦准则的球面并联机构解耦条件研究[J]. 机械工程学报, 2006, 41(9): 28-32.

HangLubin,WangYan,WuJun,etal.StudyontheDecouplingConditionsoftheSphericalParallelMechanismBasedontheCriterionforTopologicallyDecoupledParallelMechanisms[J].JournalofMechanicalEngineering, 2006, 41(9): 28-32.

[11]黄真，刘婧芳，李艳文.论机构的自由度[M].北京：科学出版社,2011.

[12]王英, 李秦川, 武传宇,等. 一种具有各向同性的3-PPRRR移动并联机构[J]. 中国机械工程, 2009, 20(10):1135-1140.

WangYing,LiQinchuan,WuChuanyu,etal.A3-DOF3-PPRRRTranslationalParallelMechanismwithFully-isotropy[J].ChinaMechanicalEngineering, 2009, 20(10):1135-1140.

[13]杨廷力. 机器人机构拓扑结构学[M]. 北京：机械工业出版社, 2004.

[14]GoguG.StructuralSynthesisofFully-isotropicTranslationalParallelRobotsviaTheoryofLinearTransformations[J].EuropeanJournalofMechanics-A/Solids, 2004, 23(6):1021-1039.

[15]ChenX,SunX.DexterityAnalysisofa4-UPS-RPSParallelMechanism[J].InternationalJournalofAdvancedRoboticSystems, 2012, 9(4):467-485.

(编辑苏卫国)

Analysis of a Novel Fully-isotropy 3T Parallel Mechanism

Cao Haofeng1Cao Yi1,2Qin Youlei1Ding Rui1

1.Jiangsu Key Laboratory of Advanced Food Manufacturing Equipment and Technology, Jiangnan University, Wuxi, Jiangsu, 2141222.State Key Laboratory of Mechanical System and Vibration, Shanghai Jiao Tong University , Shanghai, 200240

Abstract:To avoid the difficulties in the kinematics analysis and control brought by the existence of coupling in a PM, a novel kind of fully isotropic PM with three translational degrees of freedom was presented. This PM was connected by three limb chains between the moving platform and the fixed base. The first prismatic pairs of three limb chains were in orthogonal distribution, which made the moving platform of the mechanism have three translational degrees of freedom, and there existed a one-to-one correspondence between the input and output displacements. The mechanism’s most prominent advantages are simple kinematic pairs, three translations decoupled, simple kinematics analysis and to facilitate the mechanism motion control design. Using screw theory the degree of freedom and properties were analyzed and the active pair of the mechanism was determined. It also gave out the mechanism’s forward and inverse position and velocity analysis, workspace and movement performance. According to the relationship of input and output, Jacobi matrix was solved and fully isotropic of mechanism was verified. Thus it provides a theoretical guidance to the further applications, and also has good application prospects.

Key words:parallel mechanism(PM); kinematics; workspace; isotropy

收稿日期：2015-07-13

基金项目：国家自然科学基金资助项目(50905075)；机械系统与振动国家重点实验室开放课题资助项目(MSV201407)；江苏省食品先进制造装备技术重点实验室开放课题资助项目(FM-201402)

中图分类号:TH112

DOI：10.3969/j.issn.1004-132X.2016.10.016

作者简介：曹浩峰，男，1990年生。江南大学机械工程学院硕士研究生。主要研究方向为机器人学。曹毅(通信作者)，男，1974年生。江南大学机械工程学院副教授、博士，上海交通大学机械系统与振动国家重点实验室访问学者。秦友蕾，男，1991年生。江南大学机械工程学院硕士研究生。丁锐，男，1992年生。江南大学机械工程学院硕士研究生。