基于EKF的船舶模型预测动力定位导引控制器设计

刘　菊, 熊晓东, 汪大鹏, 李　鹏

(1. 哈尔滨工程大学，黑龙江 哈尔滨 150001； 2. 上海船舶工艺研究所，上海 200032；3.渤船重工船舶设计院，辽宁 葫芦岛 125000；4.金海重工股份有限公司，浙江 舟山，316291)



基于EKF的船舶模型预测动力定位导引控制器设计

刘菊1, 熊晓东2, 汪大鹏3, 李鹏4

(1. 哈尔滨工程大学，黑龙江 哈尔滨 150001； 2. 上海船舶工艺研究所，上海 200032；3.渤船重工船舶设计院，辽宁 葫芦岛 125000；4.金海重工股份有限公司，浙江 舟山，316291)

摘要传统的动力定位船舶导引控制系统包括产生动态目标点的导引子系统和产生导引点跟踪效果的控制子系统，用于较近的定位点之间的转移过程中。传统导引控制系统虽然已经成功地应用于动力定位控制系统中，但控制系统设计工作复杂，实际作业时不能自定义修改最大导引速度，海洋环境会对导引控制效果有所影响。本文设计了一种基于模型预测控制(MPC)的船舶动力定位导引控制系统，该控制系统不必进行导引子系统设计，可以直接处理定位点之间的导引控制，同时设计了扩展卡尔曼滤波器(EKF)为该控制器提供必要的状态估计，并进行了仿真试验，仿真结果验证了滤波器和控制器的有效性。

关键词模型预测控制约束控制导引控制扩展卡尔曼滤波器

0引言

随着船舶行业的多样化发展，船舶动力定位系统的应用越来越广泛，船舶的动力定位是指船舶出于必要原因需要从当前定位点转移到新的定位点。当船舶定位点间距离较远时，可以将船舶常速行进至新定位点附近，再启动定位导引操纵控制系统，逐渐将船舶控制到定位点。当两定位点相距不太远时，不必加速转移船舶，直接启动特定的导引操纵控制系统来引导船舶到达指定定位点。

导引操纵控制系统属于实际工程应用功能系统，实际作业时一般是根据预定义的导引速度从当前定位点产生一系列到达目标定位点的动态路径点，然后针对不同的预定导引速度设计控制器实现对动态目标点的跟踪，直至将船舶导引到目标定位点。传统的导引操纵控制系统一般包括制导子系统和控制子系统，如图1所示。导引控制子系统是基于PID控制方法，针对不同的预定导引速度设计各自的PID控制器，制导子系统在线产生一系列导引路径点作为控制系统的动态目标点。

图1　传统动力定位导引控制系统方框图

本文提出一种简洁的新型导引操纵控制方法——基于模型预测控制(MPC)的导引操纵控制，它能够实现从当前定位点低速运动至目标点附近，而无需传统的制导子系统。具体步骤如下：首先建立仿真和控制用的船舶数学模型，并进行扩展卡尔曼滤波器设计，然后进行模型预测控制器设计，之后设计了仿真试验对滤波器和控制器进行验证分析，最后给出了论文结论。

1船舶运动数学模型建立[1]

1.1参考坐标系

船舶运动数学模型分为两类：仿真模型和控制模型。仿真模型主要起到代替实船的作用，产生船舶运动状态信息；控制模型一般较仿真模型简单，用于控制器和观测器的分析和综合。不管是哪类模型，建模的时候都要首先确立船舶运动的参考系统。描述船舶运动数学模型时一般采用两种右手坐标系统：惯性坐标系统OXEYEZE(NED坐标系)和附体坐标系统OXYZ，如图2所示。其中，NED坐标系为固定于地球表面的惯性坐标系统，取作基准参考系统，规定XE轴指向正北方向，YE轴指向正东方向，ZE轴指向地心方向；附体坐标系OXYZ是原点位于船舶中某指定点O(对于水面船舶通常取作满载吃水平面的前后左右中心点)上的非惯性坐标系。

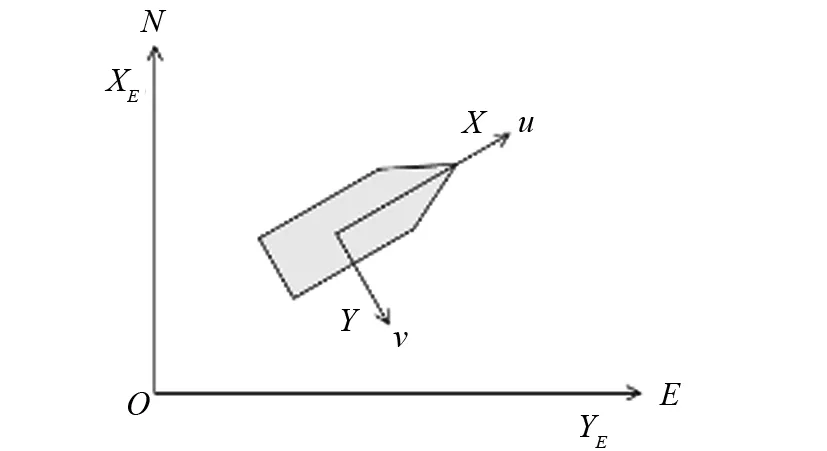
图2　船舶运动参考坐标系和运动变量

1.2仿真模型[2]

1.2.1裸船体模型

在船舶动力定位领域，关注重点是艏向角ψ和位置信息n和e的变化，即船舶在水平面内的运动。船舶水平面运动数学模型为

(1)

(2)

式中：η=[neψ]T表示船舶在NED坐标系统中的位置和艏向信息；v=[uvr]T代表船舶的纵向、横向速度和回转角速度；R(ψ)为状态转换矩阵，如式(3)所示；M=MT>0为质量和惯量矩阵；C(v)为Coriolis力和向心力矩阵；D为线性阻尼矩阵；DNL(v)为非线性阻尼矩阵；τ=[τXτYτN]T代表三个自由度上的控制输入作用；w代表环境干扰。

1.2.2环境干扰模型

环境干扰包括风浪流的低频干扰和高频干扰。对于低频干扰，要对风、浪、流分别建模，不失一般性只需考虑风的影响，认为w=[XWindYWindNWind]T。作用于船体上的平均风干扰力和力矩为

(3)

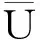
海洋环境的高频干扰以高频运动分量的形式叠加到低频运动分量上。波频模型如下:

(4)

式中：ξ∈R6×1为高频分量的状态向量；Aw∈R6×6为与海洋环境相关的矩阵；Ew∈R6×3、Cw∈R3×6为定值矩阵。

1.2.3测量模型

系统的测量模型为

(5)

式中：v为测量白噪声。

1.3控制模型[3]

控制器和观测器分析和综合是需要用到控制模型。控制模型如下:

(6)

式中：b∈R3为缓慢变化的环境低频干扰。

2扩展卡尔曼滤波器(EKF)

2.1基于状态估计的滤波模型

(7)

2.2扩展卡尔曼算法

(8)

式中：C=[CwI3×303×303×3]；

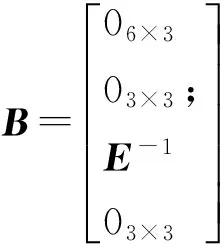
动力定位船舶在进行导引操纵时，其航向ψ变化较小，在ψ附近对模型进行线性化

(9)

(10)

式中：Fk=I-TsA；Δ=TsB；Γ=TsE，其中Ts为仿真步长；下标k表示第k仿真时刻。

EKF算法如下：

状态预测

(11)

协方差预测

(12)

残差

(13)

残差协方差

(14)

次优卡尔曼增益

(15)

状态估计

(16)

协方差估计

(17)

滤波步骤如下。

(2) 执行上述EKF算法。

(3) 如不满足结束条件，k+1。

(4) 进入步骤(1)。

3基于模型预测控制的定位导引操纵控制器[4]

模型预测控制在工业界和学术界都得到了持续的关注。其本身固有的优化功能和鲁棒性使其在船舶运动控制领域具有良好的发展前景。

模型预测控制系统的设计是基于系统状态空间数学模型的。假定控制系统的状态信息为xm=[ηTvTbT]T，在进行状态的向前预测时所需要的当前状态信息xm(k)是观测器传递过来的当前估计信息。假设采用周期为Ts，将低频控制模型的微分代数方程(11)～(13)进行一阶前向欧拉离散得到差分代数方程，作为控制器的预测模型。如果以x+表示下一时刻的状态信息，则有

(18)

(19)

式中：下标m代表与船舶模型相关；

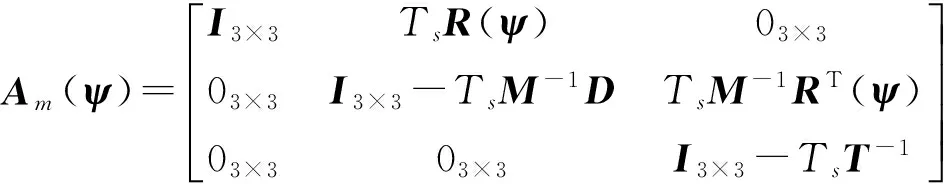
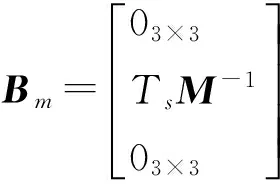
对于预测时域为Np的滚动时域控制，由于船舶的惯性大，因此滚动时域内可认为Am(ψ)可以在滚动时域初始时刻的艏向ψ0附近进行线性化得到Am。得到线性离散状态空间方程:

(20)

式中：k=0,1,…,Np-1代表预测步数，其中N为预测时域长度。为方便构建预测模型，定义以下变量:

(21)

(22)

选取x(k)=[Δxm(k)Ty(k)T]T作为预测控制系统的新状态。原船舶模型等价转化为以下扩展模型。

(23)

(24)

不失一般性以后均以下标代表预测步数；

3.1预测模型

根据状态空间模型(A，B，C)，状态预测如下:

同理得到输出预测模型

(25)

F=[(CA)T(CA2)T(CA3)T…(CANp)T]T。

3.2预测控制

假定期望输出为yd，选取代价函数如下。

(26)

(27)

对应的最优控制序列满足以下条件。

对应的最优控制序列为

(28)

以上为系统无约束时的预测控制最优解，鉴于实际系统的约束，需要满足状态软约束xmin≤xk≤xmax和输入硬约束Δumin≤Δuk≤Δumax、umin≤uk≤umax。为方便优化，将约束条件写成如下形式。

(29)

控制幅度约束：

控制增量约束：

状态约束：

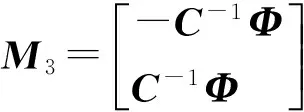
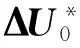
(30)

4仿真试验

四级海情下，船舶受海洋环境干扰无动力自由漂浮，仿真轨迹和估计轨迹如图3所示，各状态估计和仿真对比如图4～图6所示。由图示可知，滤波器成功地滤去了船舶运动的高频分量，估计值与仿真或者测量值接近。

图3　估计轨迹和测量轨迹的对比

图4　位置估计值和测量值对比

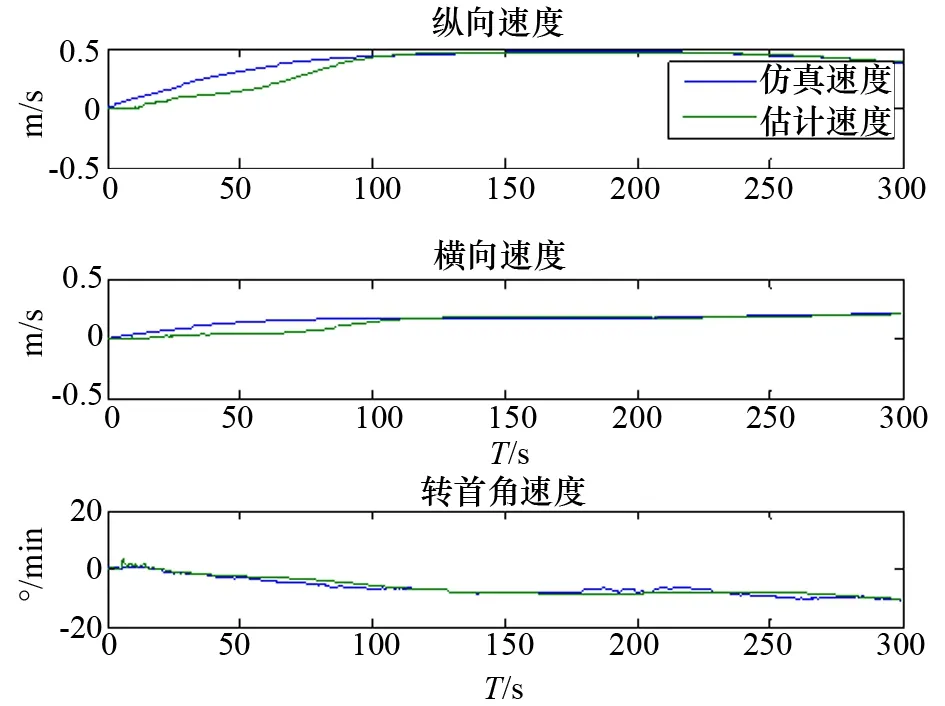
图5　速度的估计值和仿真值对比

图6　环境干扰的估计值和仿真值对比

船舶初始位置和艏向为yinit=[0 m 0 m 10°]T，期望位置为yd=[20 m 15 m 10°]T。控制器参数如下：预测时域NP=50，控制时域NC=5，输出输入权值矩阵Q=diag(103,103，106)、R=diag(10-6,10-6,10-8)。图7为导引过程船舶运动轨迹图，导引过程中的状态信息如图7～图9所示。

图7　导引过程中的船舶轨迹

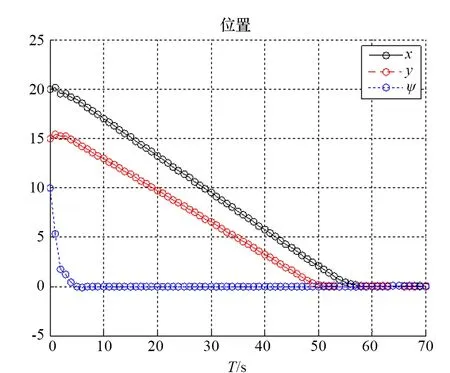
图8　导引过程中的位置和艏向

5结论

根据仿真结果可以看到，滤波器成功地滤去了船舶运动的高频分量，滤波效果能够满足控制系统的需要，同时卡尔曼滤波器(EKF)的模型预测控制系统能够有效地进行定位点之间的导引操纵。

6结束语

图9　导引过程中的速度信息

船舶动力控制系统中传统的PID控制器由于局部有效性和较差的鲁棒性限制了其远距离定位的控制效果，为保证控制效果必须设计导引系统，逐步产生动态新目标点，逐步地引导船舶到达最终目标点，增加了控制系统的复杂度。基于卡尔曼滤波器(EKF)的模型预测控制固有的优化功能和鲁棒性使其可以实现并且简化导引操纵过程，其优势如下。

(1) 结构更简洁。整个控制系统不再需要制导系统，制导算法设计及实现不再必要。

(2) 使用更方便。控制器参数调试更简单，不同海洋环境下也能低速运动至目标点附近，而不必重新设计不同的控制器参数。

(3) 更高的经济性。MPC本质上是一种最优控制方法，产生的控制输入是某种形式上的最优控制，能够减少船舶动力控制能耗和控制器磨损。

参考文献

[1]贾欣乐,杨盐生.船舶运动数学模型[M].大连：大连海事大学出版社,1998.

[2]Konsberg. Operator Manual: Kongsberg K-Pos DP-2[M].Konsberg Maritime AS， 2006.

[3]Wang L. Model Predictive Control System Design and Implementation Using MATLAB[J]. Springer Berlin, 2009, 39(12):110-114.

[4]Thor I， Fossen. Marine Control Systems: Guidance, Navigation and Control of Ships, Rigs and Underwater Vehicles[M]. Marine Cybernetics,2002.

EKF Based Model Predictive Controller Design for Dynamic Positioning Ship Guidance Control

LIU Ju1， XIONG Xiao-dong2， WANG Da-peng3， LI Peng4

(1. Harbin Engineering University, Harbin Heilongjiang 150001, China;2.Shanghai Shipbuilding Technology Research Institute, Shanghai 200032, China;3. Bohai Shipbuilding Heavy Industry Co., Ltd., Huludao Liaoning 125000, China;4.Jinhai Heavy Industry Co., Ltd., Zhoushan Zhejiang 316291, China)

AbstractTraditional guidance control system of dynamic positioning ship includes a guidance subsystem generating path points toward target dynamic positioning point and a control subsystem performing path-point tracking during the transfer process between the current and next dynamic positioning points. The conventional guidance control system has been successfully applied to dynamic positioning control system, but the control system is complicated to design and tune in varying sea. This paper presented a Model Predictive Control (MPC) based guidance controller for the dynamic positioning ship while not necessary to design the guidance subsystem, directly controlling the dynamic positioning ship toward the range of the target point. Meanwhile an Extended Kalman Filter (EKF) was designed to provide the necessary state estimation for the controller. Simulation experiments were carried out to verify the efficiency of the filter and the controller. The simulation results demonstrate the efficiency of the presented filter and controller.

KeywordsModel predictive controlConstrained controlGuidance controlExtended Kalman Filter(EKF)

中图分类号U662

文献标志码A

作者简介：刘菊(1986-)，女，博士研究生，研究方向为基于模型预测控制的动力定位。