电子罗盘在倾斜状态下校准算法研究
2016-06-02中国船舶重工集团公司第七一研究所龚天平
中国船舶重工集团公司第七一○研究所 龚天平
电子罗盘在倾斜状态下校准算法研究
中国船舶重工集团公司第七一○研究所 龚天平
【摘要】针对电子罗盘在磁航向测量中存在的各种误差,分析了电子罗盘(EMC)系统误差的形成原因与机理,在此基础上系统地研究了在任意姿态下电子罗盘磁航向误差校正问题,并且具体给出了2种误差系数的求解方法以及相应的误差补偿方法。多位置转台实验验证了该方法的有效性和实用性,校准后的电子罗盘精度由3.2°提高到0.4°,满足了导航系统的需求。
【关键词】电子罗盘;航向误差;误差补偿;校准
0 引言
电子罗盘用于测量载体姿态,广泛应用于航空、航天、航海、水中兵器、石油钻井、汽车等需要定向和导航的领域。由于使用场合往往存在软硬磁环境干扰导致电子罗盘精度降低,所以需要对电子罗盘进行修正校准。在实验室内经过试验研究发现,软硬磁环境干扰引起的电子罗盘误差主要表现为两方面:一种是对传感器零位的影响;另一种是对其灵敏度的影响。
目前,电子罗盘有平面校准(椭圆拟合)和空间校准(椭球拟合)两种算法。平面校准法主要用于不便于空间翻转的大型载体,例如飞机、轮船、汽车等等。采用把装有电子罗盘的载体在水平面内旋转一周连续采样或用8点法每隔45°采样的方法找出三轴磁通量的圆心与半径。空间校准法主要用于可以方便进行翻转的小型载体,例如手机、平板电脑等等手持设备。采用把装有电子罗盘的载体在空间旋转连续采样或用12点法或24点法采样的方法找出三轴磁通量的球心与半径。
1 电子罗盘校准算法简介
本文主要介绍平面校准算法。在没有误差的情况下,X、Y轴的输出对应关系可用图1表示,在坐标系上映射出一个圆。
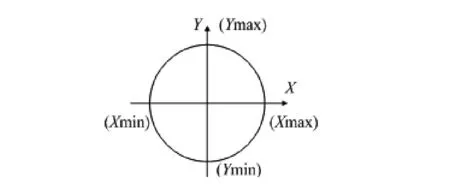
图1 无误差时传感器输出关系
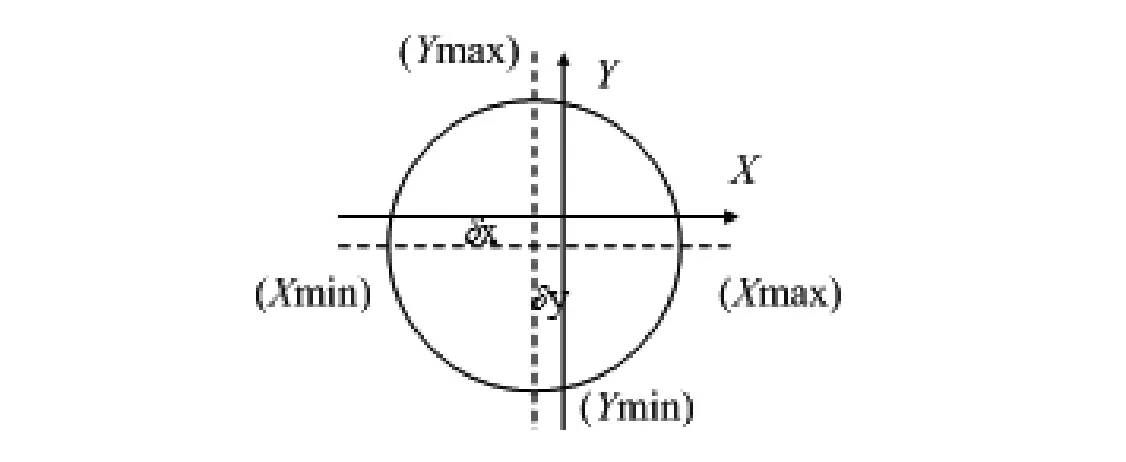
图2 有零位误差时传感器输出关系
(1)零位补偿
当X轴和Y轴有零位误差时如图2所示。
那么X,Y的零位为:
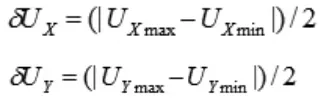
修正值为:
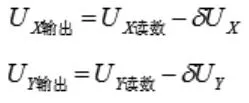
(2)灵敏度补偿
当X轴和Y轴的输出灵敏度不一致时,这个圆变为一个椭圆,如图3所示。
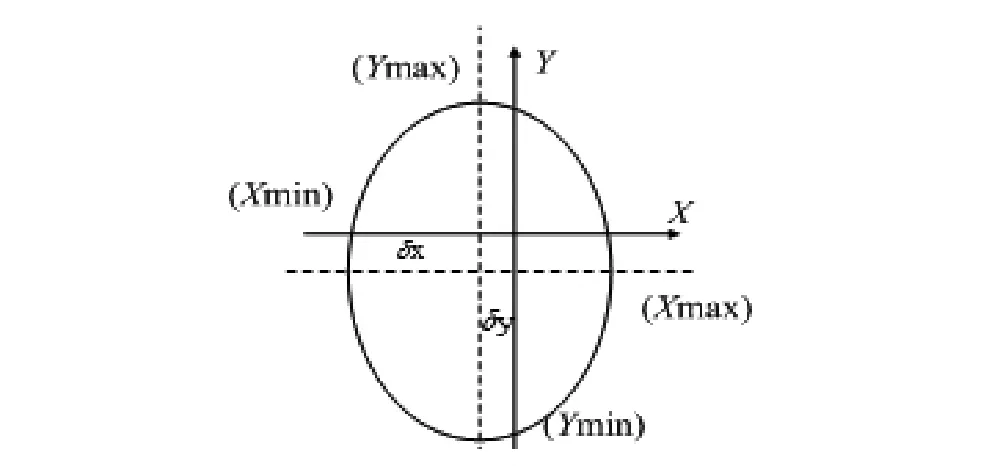
图3 有灵敏度误差时传感器输出关系
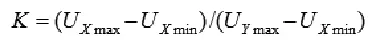
假设以X轴输出为基准,那么为:
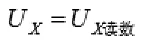
修正后:
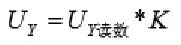
在平面校准法中,在采样时必须保证载体在水平面内旋转,但在用户实际现场使用时,由于转台、地面等平面不能保证绝对水平,往往有3°~5°甚至更大的倾斜角,且旋转过程中,倾斜角不断变化,这就会给计算带来较大偏差,校准后精度得不到保证,经常发生越校准电子罗盘精度反而越差的情况。
在某次用户现场校准数据见表1。
2 电子罗盘在倾斜状态下校准算法
电子罗盘在倾斜状态下校准算法如下:在校准采样磁通量过程中,通过电子罗盘自带的倾斜角传感器同步采样倾斜角数据。采样结束后,用倾斜角修正磁通量,将其转换为水平面内的磁通量,然后再用平面校准法计算得出三轴磁通量的圆心与半径。
如图4所示,设地磁场为H,其在正交坐标系的投影是Hx、Hy、Hz,磁倾角为θ,三轴磁通量的圆心为MX0,MY0,半径为SX,SY,采样的最大值和最小值分别是MXmax、MXmin、MYmax、MYmin、MZmax、MZmin。
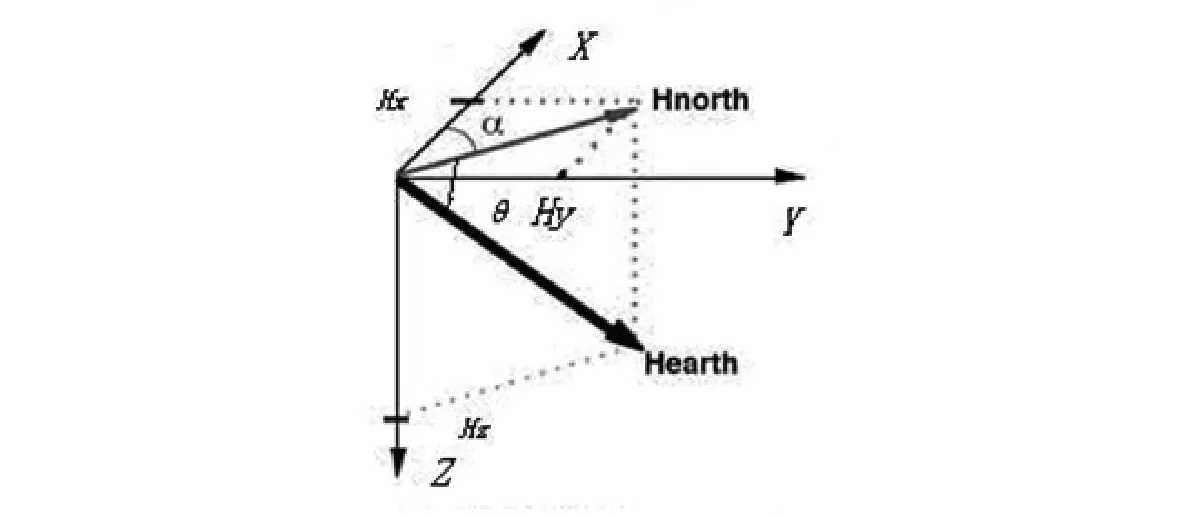
图4 地磁场分量矢量图
那么采样的几个极值点与地磁场存在下式关系:

在平面校准法中,三轴磁通量的圆心与半径由下式求得:

可见,只要准确找到几个极值点,就可以计算出三轴磁通量的圆心与半径。而在实际使用过程中,由于各种原因导致校准过程采样时,载体不能保证在水平面内运动,这样采样到的极值点就与水平面内的实际计算需求的极值点存在偏差。假设在采样几个极值点时,载体与水平面存在的夹角分别是B0、B1、B2、B3,垂直面与铅垂线的夹角是B4、B5。那么采样的几个极值点与地磁场存在下式关系:

把式(3)展开得出:
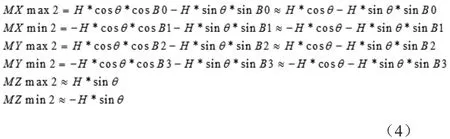
把式(1)和式(3)联合得出:
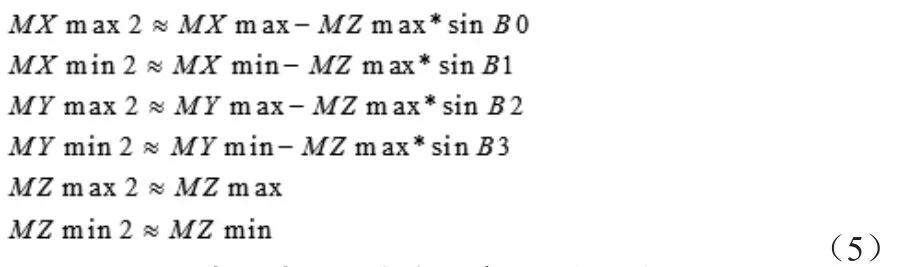
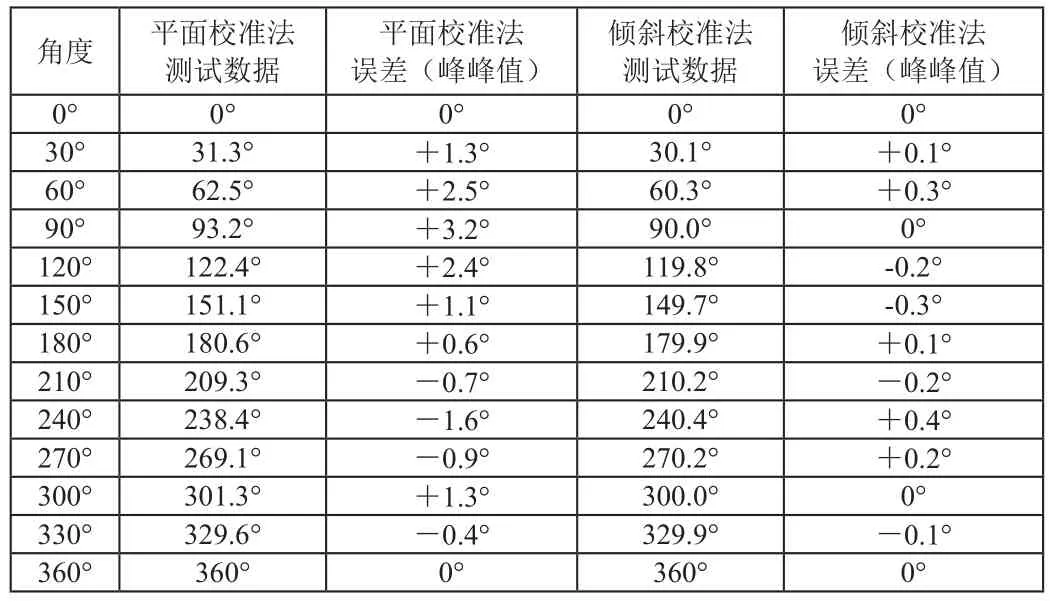
表1 电子罗盘在用户现场校准数据
由(5)式可以继续推导得出:
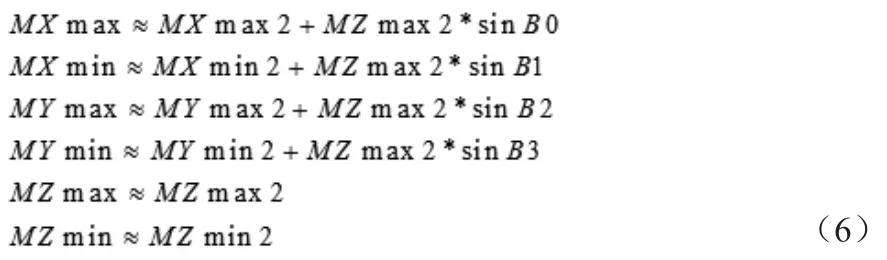
其中,MXmax、MXmin、MYmax、MYmin、MZmax、MZmin由采样得出,B0、B1、B2、B3可以由倾斜角传感器测量计算得出。
用该算法改进后的电子罗盘在某次用户现场校准数据见表1。
3 结束语
传统的水平面校准法对用户要求较高,而实际使用过程中,很难找到专业实验室里才有的水平转台,本文所述的电子罗盘倾斜在倾斜状态下的校准算法可以有效克服水平面校准法的缺陷,使得电子罗盘在用户实际使用过程中的校准精度由3.2°提高到0.4°,具有很强工程应用价值。
参考文献
[1]李艳,管斌,王成宾.电子磁罗盘航向角误差推导及分析[J].仪器仪表学报,2013,34(7)﹕1566-1572.
[2]孙宏伟,房建成,李艳.椭圆拟合方法在磁罗盘罗差校准中的应用[J].光学精密工程,2009,17(12)﹕ 3034-3039.
[3]李智,李翔.基于椭球假设的三轴电子罗盘罗差补偿研[J].仪器仪表学报,2011,32(10)﹕2210-2215.
[4]秦勇,赵杰,王晓宇.基于椭圆拟合误差补偿算法的数字磁罗盘[J].吉掉大学学报,2009,39(2)﹕490-493.
[5]KIM J,LEE J G,SUNG T K,et aI.Compensationgyroscope elTOrs and GPS /DR integration[C]//IEEEPLANS,96.Piscataway﹕IEEE Press,1996﹕464-470.
