基于GA-GRNN的露天矿山边坡稳定性评价*

陈　梵　章　光　王丹丹　李墨潇

(武汉理工大学资源与环境工程学院)



基于GA-GRNN的露天矿山边坡稳定性评价*

陈梵章光王丹丹李墨潇

(武汉理工大学资源与环境工程学院)

摘要边坡失稳是露天矿山常见的地质灾害，快速确定边坡的稳定状态对于确保矿山安全生产意义重大。利用广义回归神经网络(General regression network, GRNN)的非线性逼近性能并结合遗传算法(Genetic algorithm,GA)的非线性寻优性能对某露天矿山的边坡安全系数进行了预测，结果表明：基于遗传算法优化的广义回归神经网络(GA-GRNN)对露天矿山边坡安全系数的预测结果较为精确，且预测速度较快，为实际工程中快速判断露天矿山边坡的稳定状态提供参考。

关键词露天矿山边坡稳定性安全系数遗传算法广义回归神经网络

目前，边坡稳定性分析方法主要有极限平衡法、工程地质分析法、数值模拟法、可靠性分析法等，该类方法虽然考虑了边坡的主要因素，但由于计算繁琐，较难准确描述非线性特征，且未能有效顾及边坡稳定性影响因素的模糊性、随机性、不确定性等特点，因而无法实现对边坡稳定性进行快速预测[1-3]。人工神经网络(Artificial neural network,ANN)与各类算法的结合可实现对边坡稳定性的快速、准确预测，在一定程度上弥补了传统方法的不足[4-8]。广义回归神经网络(GRNN)的非线性逼近性能及容错率均较优，可适用于小样本问题，且其结构固定，可更快的进行训练，但该算法通过人为调节参数光滑因子(σ)，对预测精度影响较大[9]。为此，采用遗传算法优化的广义回归神经网络(GA-GRNN)对某露天矿山边坡安全系数进行预测，有助于降低人为因素的影响，提高预测精度。

1算法原理

1.1广义回归神经网络

1.2基于遗传算法优化广义回归神经网络

1.2.1遗传算法原理

遗传算法(GA)是一种有效的全局寻优算法，每次通过迭代借助交叉、突变产生新个体，逐渐扩大搜索范围，可高效寻求全局最优解。该算法的基本要素为染色体编码方法、适应度函数、遗传操作和运行参数。用遗传算法对GRNN建立的数学模型进行优化，在求解所优化的问题时不要求可微和连续，也无需了解函数的具体形式，即可实现离散变量的全局寻优。

1.2.2GA-GRNN预测步骤

GRNN的光滑因子(σ)需人为调节，且各神经元的σ都设置为同一个值，网络的训练过程即为对σ的单值寻优过程，并未考虑不同σ取值对输出结果精度的影响，在一定程度上降低了网络的预测精度。通过遗传算法对GRNN进行优化，将每个σ值作为一个独立变量，根据不同的神经元对输出结果的不同影响程度，选取每个神经元对应的最优光滑因子，可消除采用单个光滑因子对网络预测精度的影响。通过遗传算法中的选择、交叉、变异等操作筛选个体，淘汰适应度低的个体，适应度高的个体则被保留，产生新一代群体，通过反复循环上述流程，直至满足条件为止。因而，采用遗传算法搜索最优σ值，建立了GA-GRNN模型，具体步骤：①确定遗传算法参数；②遗传算法初始化，生成种群规模为NIND的GRNN光滑因子初始种群，进化代数g=0;③读入学习样本进行网络训练，按给定的适应度函数进行适应度评价；④采用遗传算法按各个体的适应度大小进行选择、交叉和变异操作，得到新的种群P(g+1)，进化代数g=g+1；⑤判断是否达到最大进化代数，若已达到，则停止计算，返回适应度最高的个体；否则转至③，直至达到最大进化代数；⑥输出适应度最高的个体对应的实值数，即为最优的σ值；⑦用最优的σ值建立GA-GRNN模型，对测试样本进行预测。

2应用实例

在构建GA-GRNN模型前，有必要选择与边坡失稳密切相关的因素(容重、黏聚力、内摩擦角、边坡角、边坡高度、孔隙水压力比)作为输入变量。将上述6个因素作为GRNN的输入单元，输出单元为边坡的安全系数f。遗传算法的种群规模为50，交叉概率0.6，变异概率0.1，迭代次数100。以某露天矿山边坡数据为学习样本和测试样本，见表1[4-5]。

以表1中前32组数据为学习样本，后5组数据为测试样本。采用基于遗传算法优化的BP神经网络(GA-BP)、人为选取σ值(σ取0.3)的GRNN以及GA-GRNN进行边坡危险性预测试验，结果见表2。GA-GRNN的适应度曲线见图1。为准确评价各模型性能，采用均方误差(Mean square error,MSE)、平均误差百分率(Mean percentage error，MAPE)评价模型精度，采用威尔莫特一致性指数评价模型的泛化性(Willmott's index of agreement，WIA)。

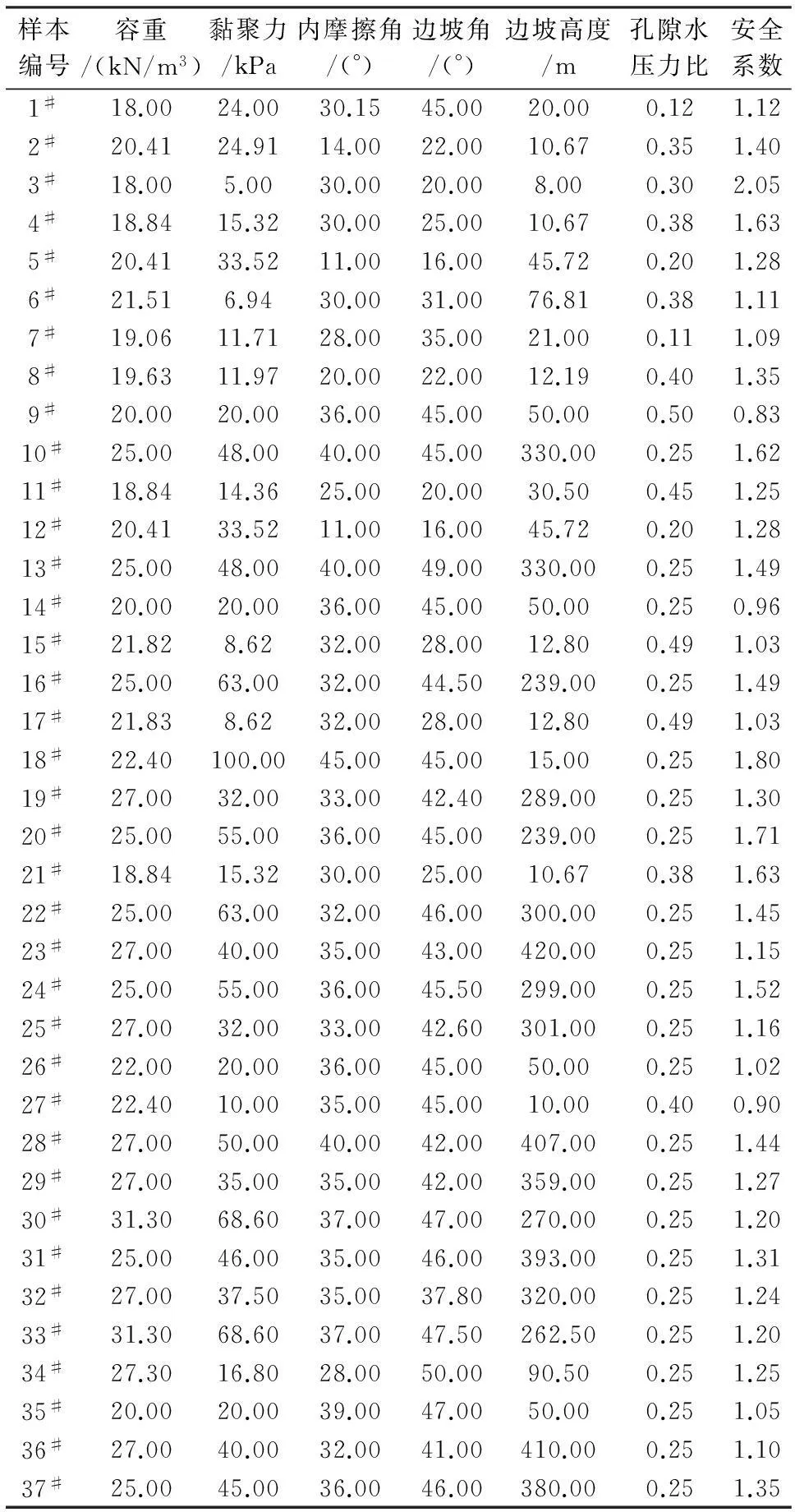
表1　样本数据

表2　安全系数预测误差

由表2、图1可知：当种群进化至100代时，平均适应度极剧下降，GA-GRNN的适应度达到了最佳值。GA-GRNN的平均绝对误差(2.57%)及最大相对误差(小于4%)均优于GA-BP及GRNN。经计算得：MSE=0.29，MAPE=2.20，WIA=0.98，表明GA-GRNN模型具有较强的泛化能力，对新样本具有很好的适应能力。

3结论

(1)在考虑边坡稳定性多种影响因素的情况下，GA-GRNN可实现对露天矿山边坡安全系数的高精度预测，预测结果与实际值的最大误差小于4%，可满足现场工程需要。

(2)GA-GRNN预测的准确性和稳定性优于GA-BP，且GA-GRNN的预测运算时间远远小于GA-BP，可实现对露天矿山边坡安全系数的快速预测。

(3)GA-GRNN在预测过程中，无人为调节因素，输出数据唯一，无需进行多次比较，实用性较强。

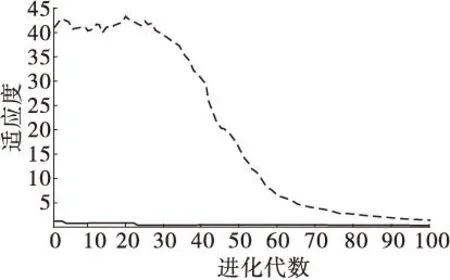
图1　GA-GRNN适应度曲线

参考文献

[1]倪凯军，安海堂，张卫强.降雨入渗对边坡稳定性影响的试验研究[J].现代矿业，2015(11)：176-179.

[2]宋亮华，刘涛.基于重整化群语模糊可靠度法的边坡稳定性分析[J].现代矿业，2015(6)：163-164.

[3]杨天鸿，张锋春，于庆磊，等.露天矿高陡边坡稳定性研究现状及发展趋势[J].岩土力学，2011，32(5)：1437-1451.

[4]刘先珊，周创兵.改进的边坡岩体稳定性预测模型研究[J].岩石力学与工程学报，2005，24(19)：3492-3498.

[5]贺可强，雷建和.边坡稳定性的神经网络预测研究[J].地质与勘探，2001，37(6)：72-75.

[6]胡卫东，曹文贵.基于粒子群BP网络混合算法的边坡稳定性评价[J].铁道科学与工程学报，2015(1)：66-71.

[7]刘思思.基于神经网络及遗传算法技术的边坡稳定性评价研究[D].长沙：中南林业科技大学，2006.

[8]陈明.MATLAB神经网络原理与实例精解[M].北京：清华大学出版社，2013.

[9]习施彦，韩力群，廉小亲.神经网络设计方法与实例分析[M].北京：北京邮电大学出版社，2009.

(收稿日期2015-06-25)

*高等学校博士学科点专项科研基金(编号：20120143110005)。

陈梵(1993—)，男，硕士研究生，430070 湖北省武汉市洪山区珞狮路122号。