基于ANSYS模拟的边坡稳定性影响因素分析

甘　露

(成都建筑材料工业设计研究院有限公司)



基于ANSYS模拟的边坡稳定性影响因素分析

甘露

(成都建筑材料工业设计研究院有限公司)

摘要逐一分析边坡稳定性的影响因素，在ANSYS模拟时利用强度折减，得出在仅改变这一参数时相应的安全系数，应用图表直观地反映了安全系数与这一参数的变化情况。并得出以下结果：容重、边坡高度以及边坡角度增加时边坡稳定性降低；粘聚力与内摩擦角增加时边坡稳定性增加；容重、边坡高度、边坡角、粘聚力、内摩擦角这5个参数对边坡的稳定性影响显著；弹性模量与泊松比对边坡稳定性的影响无明显的单调趋势，对边坡稳定性影响较小。

关键词边坡稳定性影响因素ANSYS模拟强度折减

随着我国经济的快速发展，各地铁路、公路、矿业以及水利建设也不断发展。在铁路、公路、矿业与水利建设中，不可避免的会修建不同地质状况的边坡，由于边坡稳定性影响因素复杂，边坡失稳的情况时常发生，严重影响到铁路、公路、矿业与水利工程的安全以及建设成本。为探明各因数对边坡稳定性的影响，本文利用ANSYS，逐一模拟了7个影响因素(弹性模量、泊松比、容重、粘聚力、内摩擦角、边坡高度以及边坡角度)对边坡稳定性的影响。模拟时对粘聚力与内摩擦角进行了反复强度折减，当刚好出现模拟不收敛时的折减系数即为边坡的安全系数。用安全系数表征边坡的稳定性，旨在充分了解各因素对边坡的稳定性影响，为边坡的合理建设、稳定性预测以及模拟工作提供参考依据。

1影响边坡稳定性的因素

岩土体开挖后，边坡失稳的实质是边坡岩土体中的剪应力大于岩土体的抗剪强度。因而凡是直接或间接影响岩土体抗剪强度的因素都将影响边坡的稳定性。通过查阅资料和分析，影响边坡稳定性的因素主要有[1-2]：

(1)边坡材料力学特性参数。弹性模量(E)、泊松比(v)、内摩擦角(φ)、粘聚力(C)和容重(γ)等参数。

(2)边坡的几何尺寸参数。边坡高度、坡面角和边坡边界尺寸等。考虑到在应用ANSYS模拟时，模型对边界尺寸的敏感性(坡脚到最近边界的水平距离应大于边坡高度的1.5倍，坡顶到最近边界的水平距离应大于坡高度的2.5倍，同时上下边界总距离应大于2倍的边坡高度[3])，因而模拟时利用固定边界尺寸的方式，可以有效避开边界尺寸对边坡稳定性的影响。

(3)边坡外部荷载。地震力、重力和构造应力等。但考虑到地震力、构造地应力难以获得，故而ANSYS分析中仅考虑重力对边坡稳定性分析。

2初始输入力学参数的确定

通过试验直接获得原始力学参数。在利用ANSYS模拟时，直接输入ANSYS软件中的参数为初始输入力学参数。原始力学参数与初始输入力学参数并非绝对一致，关键在于屈服准则的选取。

2.1屈服准则选取

有限元强度折减法分析边坡稳定性时，采用弹塑性本构，Drucker-Prager(以下简称D-P)准则，常用的屈服准则有5种[4]，见表1。

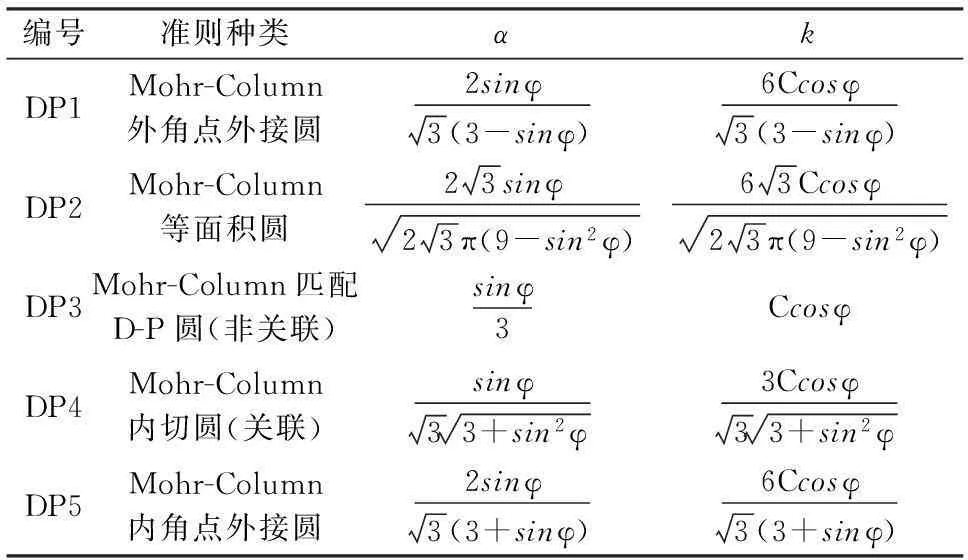
表1　屈服准则

注：α,k为与岩土材料内摩擦φ、粘聚力C有关的常数。

在ANSYS模拟中只能使用DP1准则，其它准则需要对粘聚力与内摩擦角参数进行换算，这就是原始力学参数与初始输入力学参数不完全一致的原因。在实际应用时发现，DP3求得的安全系数误差最小[3]，所以，这里采用DP3准则。

2.2原始力学参数的选取与换算

2.2.1原始力学参数的选取

对于不同的边坡，原始力学参数并非一个固定值，通过模拟得出边坡稳定性随着某一参数变化(其它参数不变)引起的边坡稳定性变化情况，故而原始力学参数是直接通过假设而获得的常见力学参数。本次采用的原始力学参数见表2。

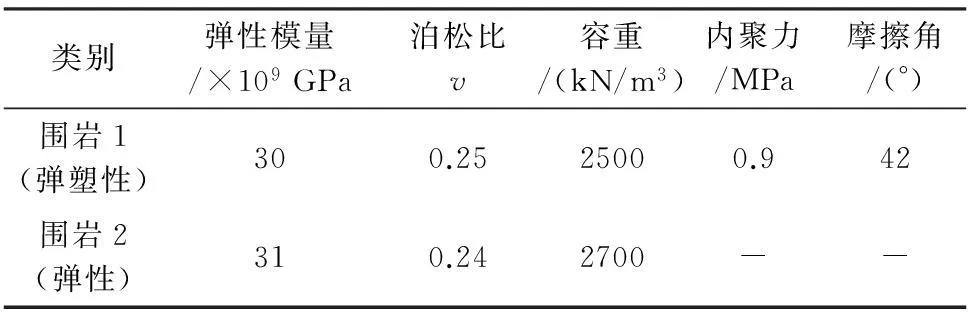
表2　原始力学参数

注：最底层(围岩2)为弹性层，没有这一弹性层，边坡可能会发生突变式破坏，并未形成塑性贯通，所得到的模拟结果与设计概念不相符合。

2.2.2原始力学参数的换算

因本次模拟采用的屈服准则为DP3，故而需要将内摩擦角与粘聚力参数进行换算。假设原始力学参数中内摩擦角为φ0，粘聚力为C0，利用DP1和DP3相等的原则，计算出在DP1准则下的内摩擦角φ与粘聚力C。 经计算可得[5]：

轮回是叶芝神秘主义思想下不可不提的主题。“轮回”本是古印度婆罗门教主要教义之一，认为死亡仅仅是走向下一个轮回，后被佛教沿袭并为其注入新的教义。“谓众生于六道中犹如车轮旋转，循环不已，流转无穷。众生由惑业之因贪、嗔、痴三毒招感三界、六道的生死轮转，恰如车轮的回转，永无止尽。故称轮回。”而该论文所指的“轮回”是叶芝在自己所处的时代大背景下，基于创作主题和目的的需要，对“轮回”的本意建构了自己的理解，使之能够充分地表达他的思想。

(1)

(2)

将原始力学参数中φ0带入式(1)，求出φ，后将φ、φ0以及C0带入式(2)，求出C。换算后的数据见表3。

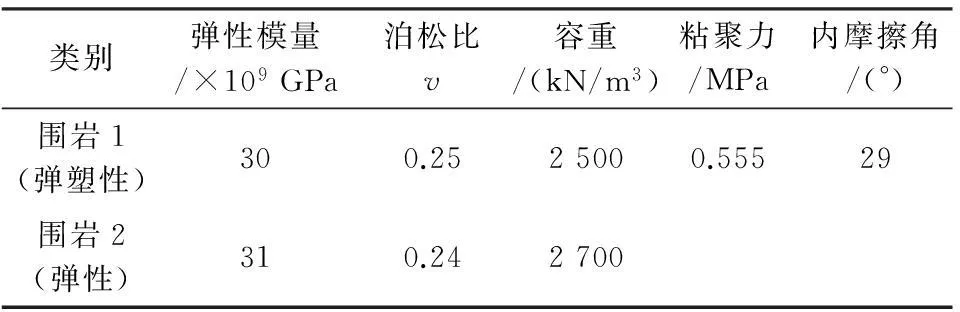
表3　初始输入力学参数

3有限元强度折减

将岩土体的抗剪强度指标粘聚力与内摩擦角进行折减，见式(3)、式(4)。 把经计算出的C′和φ′重新代入有限元中进行模拟计算，反复迭代，直到有限元计算不收敛，边坡破坏。此时对应的强度折减系数K即为边坡的安全系数[6-7]。

(3)

(4)

式中,φ、C分别为折减前的初始输入力学参数；φ′、C′分别为折减后的初始输入力学参数；K为折减系数。

经过式(3)、式(4)折减后，见表4。

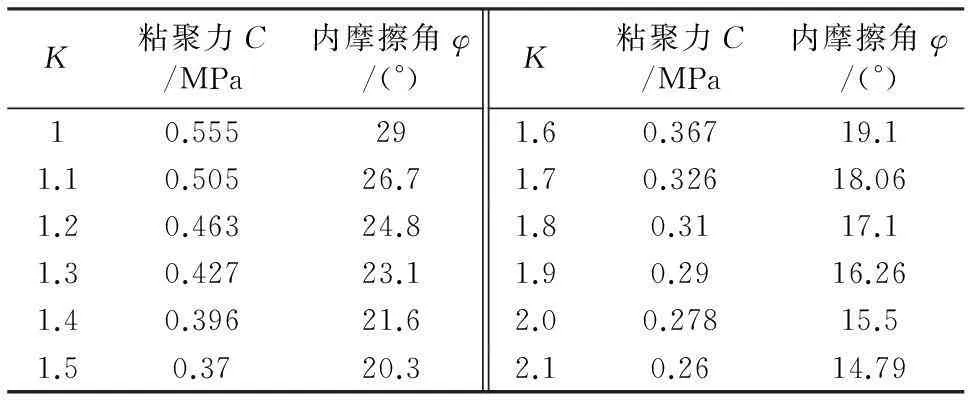
表4　折减安全系数与C、φ间的关系

4模拟不同影响因素下边坡的稳定性

计算模型见图1，模型网格划分见图2。模拟时假定整个边坡为均质单一的岩土体边坡，且仅受边坡自身重力影响。初始输入力学参数：E=30×109GPa、ν=0.25、γ=2 500 kN/m3、C=0.555 MPa、φ=29°；边坡几何尺寸参数：H=350 m、θ=40°；边坡外部荷载：g=9.8 m/s2。基于有限元强度折减法理论，利用ANSYS进行模拟计算分析。

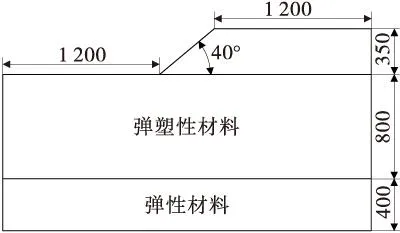
图1　计算模型(单位:m)

图2　模型网格划分示意

为了得出某一因素对边坡稳定性的影响，计算时只改变这一影响因素的参数，其余所有影响因素的参数以及ANSYS的操作方式均保持不变[9]。

4.1弹性模量

仅改变弹性模量，其他条件不变，模拟分析后，得出边坡安全系数随弹性模量的变化见表5。

表5　安全系数与弹性模量的关系

注：“-”表示模拟时边坡整体变形较大。

仅改变泊松比，其他条件不变，模拟分析后，得出边坡安全系数随泊松比的变化见表6。

表6　安全系数与泊松比的关系

4.3容重

仅改变容重,其他条件不变，经模拟分析后,得出边坡安全系数随容重变化变化见表7。

表7　安全系数与容重的关系

4.4粘聚力

仅改变粘聚力，其他条件不变，经模拟分析后，得出边坡安全系数随粘聚力的变化见表8。

表8　安全系数与黏聚力的关系

4.5内摩擦角

仅改变内摩擦角，其他条件不变，经模拟分析后，得出边坡安全系数随内摩擦角的变化见表9。

表9　安全系数与内摩擦角的关系

4.6边坡高度

仅改变边坡高度，其他条件不变，经模拟分析后，边坡安全系数随边坡高度的变化见表10。

表10　安全系数与边坡高度的关系

4.7边坡角

仅改变边坡角度，其他条件不变，经模拟分析后，得出边坡安全系数随边坡角度的变化见表11。

表11　安全系数与边坡角度的关系

5模拟结果分析

(1)根据表5～表6可知，当弹性模量与泊松比不断增加时，安全系数的值变化不大且不断波动。由此可知：弹性模量与泊松比的变化对边坡的稳定性影响不大，边坡稳定性与弹性模量及泊松比无明显的单调关系。

(2)根据表7、表10、表11可知，当容重、边坡高度以及边坡角度不断增加时，安全系数值变化大且呈现出逐渐减小的趋势。由此得出：容重、边坡高度以及边坡角度对边坡稳定性的影响显著，边坡稳定性随容重、边坡高度以及边坡角度增加而降低。

(3)根据表8、表9可知，当粘聚力与内摩擦角不断增加时，安全系数的值变化大且呈逐渐增大的现象。由此得出：粘聚力与内摩擦角对边坡稳定性的影响显著，边坡稳定性随粘聚力与内摩擦角的增加而增加。

根据以上分析可以知道，在预测边坡稳定性时，试验测定的参数弹性模量与泊松比精度不用要求太高，而容重、粘聚力、内摩擦角则需要严格控制其准确性，既可以有效预测边坡稳定性，又可以降低试验费用；严格控制边坡高度与边坡角度，以保证边坡的稳定性。

6结论

①弹性模量与泊松比的变化对边坡的稳定性影响不大，即边坡稳定性与弹性模量以及泊松比无明显的单调关系；②容重、边坡高度以及边坡角度对边坡稳定性的影响显著，边坡稳定性随容重、边坡高度以及边坡角度增加而降低；③粘聚力与内摩擦角对边坡稳定性的影响显著，边坡稳定性随粘聚力与内摩擦角的增加而增加。

参考文献

[1]聂守智.基于有限元强度折减法的边坡稳定性数值研究[D].西安：西安理工大学，2010.

[2]乔金丽.边坡稳定性分析的弹塑性有限元模型及应用[D].保定：河北大学，2005.

[3]郑颖人,赵尚毅.有限元强度折减法在土坡与岩坡中的应用[J].岩石力学与工程学报，2004,23(19):3381-3388.

[4]赵尚毅,郑颖人,刘明维,等.基于Drucker-Prager准则的边坡安全系数定义及其转换[J].岩石力学与工程学报，2006(S1):2730-2734.

[5]高恭星.用ANSYS分析边坡稳定性[J].重庆建筑，2012(9):80-83.

[6]柳林超,梁波,刁吉.基于ANSYS的有限元强度折减法求边坡安全系数[J].重庆交通大学学报：自然科学版，2009(5):899-901，910.

[7]涂国强.基于ANSYS的边坡稳定性分析[J].交通科技与经济，2009(4):70-71，74.

[8]靳楠,张静.黄土力学参数对边坡稳定性的影响[J].四川建材，2013(5):100-101.

(收稿日期2015-11-01)

Simulation of the Influence Factors of Slope Stability Based on ANSYS

Gan Lu

(Chengdu Building Materials Design and Research Institute)

AbstractIn order to analyze the influence of the factors to slope stability one by one, based on the strength reduction method of ANSYS software, the slope safety coefficient is analyzed under the condition of changing a single factor parameter value and keeping other factors unchanged,and the changing relationship of safety coefficient of the signal factor is reflected. It can concluded that the influence of the five parameters of bulk density, slope height, slope angle, cohesive force and internal friction angle to slope stability is obvious, with the increasing of the parameters values of bulk density, slope height and slope angle, the slope stability is reduced, the increasing of cohesive force and internal friction angle, the slope stability is improved;the monotonous tendency of the influence of elasticity modulus and poisson ratio to slope stability is not obvious, the influence of the two parameters to slope stability is smaller.

KeywordsSlope stability, Influence factors, ANSYS simulation, Strength reduction

甘露(1964—)，男，高级工程师，610021 四川省成都市成华大街新鸿路69号。