最大水平主应力对巷道围岩稳定性的影响研究

闫永波　陆　文　张喜涛　王俊峰

(1.西南科技大学环境与资源学院;2.西昌学院工程技术学院)



最大水平主应力对巷道围岩稳定性的影响研究

闫永波1陆文1张喜涛1王俊峰2

(1.西南科技大学环境与资源学院;2.西昌学院工程技术学院)

摘要基于金川三矿实测地应力和某分段巷道,采用理论分析，得出了σHv型应力场下巷道的最优布置夹角,针对最大水平主应力与巷道轴线呈不同夹角时的巷道布置，采用FLAC3D数值模拟软件进行数值模拟,对其应力分布、塑性区分布和围岩位移进行对比研究。结果表明，在σHv型应力场下，巷道的最优布置方式是与最大水平主应力成某一角度;当夹角达到一定程度时,巷道顶底板会出现大小相当的环向应力;引起巷道底板变形破坏的重要原因是水平应力。

关键词最大水平主应力数值模拟围岩位移

地下工程的稳定性取决于围岩性质、原岩应力场的分布、工程断面形状、以及工程支护方式等因素。地应力是引起地下工程围岩变形和破坏的主要因素,其大小和方向直接关系着地下工程围岩的稳定与否[1-4]。相关资料[5-6]显示,岩层中的水平应力在多数情况下大于垂直应力,且具有明显的方向性，巷道底鼓、顶板沉降和两帮内挤与其密切相关。郑书兵[7]、张延新等人[8]的研究也都说明了巷道的正确布置有利于其稳定。

在实际施工过程中，巷道布置常常难以与原岩应力场相适应，一是巷道的布置决定于矿床开拓方式与开采方法,难以保证巷道的走向与最大主应力方向始终一致或垂直；二是原岩在漫长的地质年代中经历多次地质构造运动,原岩应力是自重应力与历次构造运动产生的残余应力叠加的结果,最大主应力的大小和方向是变化的。因此,原岩最大主应力的方向与巷道走向(轴线方向)的夹角对于巷道围岩稳定的影响,便成了重要的研究课题。本文基于金川集团地下矿山实测原岩应力,通过理论分析和对某分段巷道进行数值模拟,探索巷道轴线与最大水平主应力的夹角对巷道稳定性的影响。

1巷道的最优布置理论分析

原岩应力实测结果表明：金川集团三矿区地下岩层的水平应力一般大于垂直应力,且水平应力具有明显的方向性;最大水平主应力与最小水平主应力的比值为1.5～2.5。

巷道顶底板的稳定性与水平应力之间有以下特点：①当巷道轴线与最大水平主应力平行时,顶底板稳定性最好;②巷道轴线与最大水平主应力相交时,其顶板变形破坏偏向巷道某一帮;③巷道轴线与最大水平主应力垂直时,顶底板稳定性最差。根据弹性力学的孔口理论,巷道截面尺寸要与原岩的正应力大小相适应,最好实现等应力轴比。金川公司地下矿山采场分段巷道为直墙拱形,宽度与高度均为5.0 m左右,因此巷道最优布置应该使原岩水平正应力与垂直主应力的比值等于1,即σn/σv=1。

按照最大水平主应力σH、最小水平主应力σh和垂直主应力σv三者数值的大小关系,将岩层中的地应力场分成3种形式,即σH型,σH>σh>σv;σHv型,σH>σv>σh;σv型,σv>σH>σh。张重远[9]等人在金川三矿区的地应力测量成果表明,三矿区最大水平主应力约是最小水平主应力的2倍,最大水平主应力σH=14.7 MPa,最小水平主应力σh=7.2 MPa,平均垂直主应力σv=11.9 MPa,σH>σv>σh，属于σHv型，可以满足σn/σv=1。任意平面上的法向应力与最小和最大水平主应力之间的表达式为

(1)

式中,α为巷道轴线与最大水平主应力方向的夹角，(°)。

将σn/σv=1代入式(1),可解得巷道布置的最优夹角：

(2)

将测量的地应力结果代入式(2),解得金川集团三矿区巷道的最优布置夹角为53°。

为进一步寻找巷道布置的最优夹角与原岩地应力场之间的关系,现设垂直主应力为12 MPa,通过式(2)，可计算出在不同的应力场状态下时，巷道在岩层中布置的最优夹角,结果见表1。

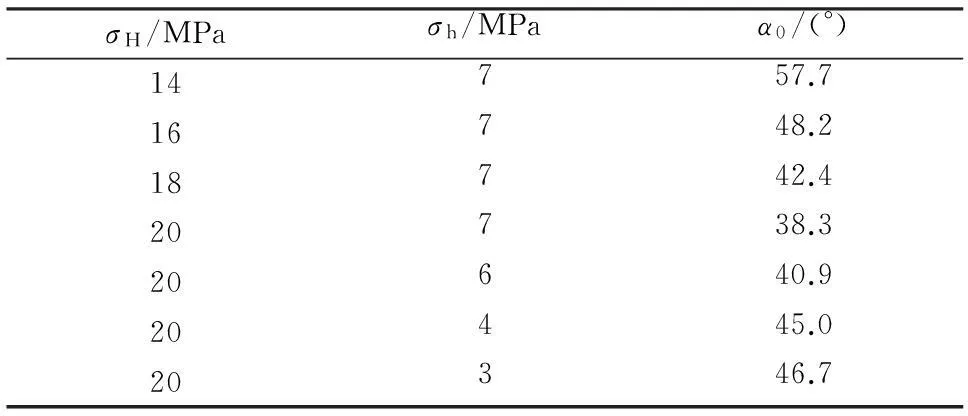
表1　不同应力状态时巷道布置最优夹角(σv =12 MPa)

当最大水平主应力固定不变时,巷道布置的最优夹角随着最小水平应力的减小而增大,即巷道布置的最优夹角偏离最大水平主应力方向。

2数值模拟及结果分析

2.1数值模型建立与模拟方案

以金川集团三矿某分段巷道为模拟对象,运用美国Itasca公司开发的三维有限差分FLAC3D软件进行数值模拟。巷道断面形状为直墙拱形,巷道尺寸(宽×高)为5.0 m×4.6 m。根据弹性力学孔口理论,地下巷道开挖引起岩体中应力重分布的范围为4倍的开挖跨度和高度。因此综合考虑巷道稳定性的各种影响因素[10],以巷道拱圆心为原点,确定所建立的计算模型尺寸(宽×长×高)为50 m×30 m×50 m,共划分59 520个单元,62 031个节点。模型采用Mohr-coulomb破坏准则,考虑到巷道埋深远远大于20倍巷道半径,故采用应力边界控制,忽略所建模型内岩体自重。

为了模拟最大水平主应力与巷道轴线不同夹角(0°～90°)下巷道围岩的应力分布和变形破坏规律,每隔10°建立一组模型,共10组模型。

2.2数值模拟参数选择

根据张重远等人的地应力测量成果,金川三矿数值模拟应力场参数选取为最大水平主应力为14.7 MPa,最小水平主应力为7.2 MPa,垂直主应力为11.9 MPa。根据实验室所做试验和前人的模拟经验选择岩石力学参数,见表2。

表2　岩石力学参数

2.3模拟结果分析

圆形巷道轴对称问题的线弹性解析表明,巷道周边将产生环向应力的最大值和径向应力的最小值。直墙拱形巷道与圆形巷道在形状上存在一定的差距,但在弹塑性条件下，直墙拱形巷道围岩的水平应力和垂直应力的数值解与圆形巷道的解析解有一定类似之处,因此在分析应力时可将顶底板围岩中水平应力以及帮部围岩中垂直应力近似看作环向应力;顶底围岩中垂直应力和帮部围岩中水平应力可近似看作径向应力。

2.3.1围岩应力分析

在不同角度下巷道布置的数值模拟结果见图1～图3。

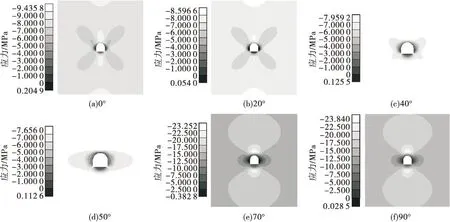
图1　不同夹角下围岩水平应力的分布

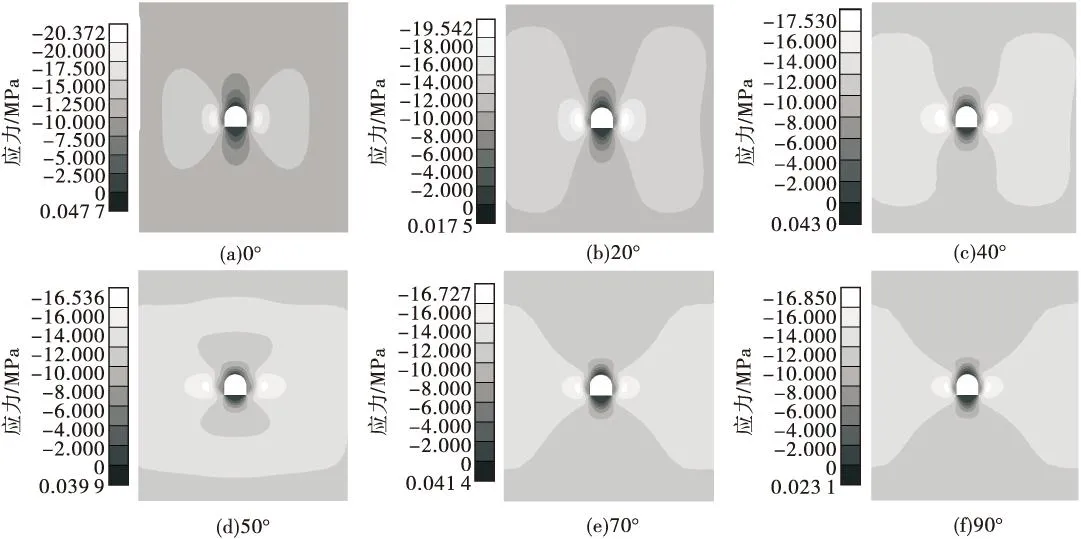
图2　不同夹角下围岩垂直主应力的分布

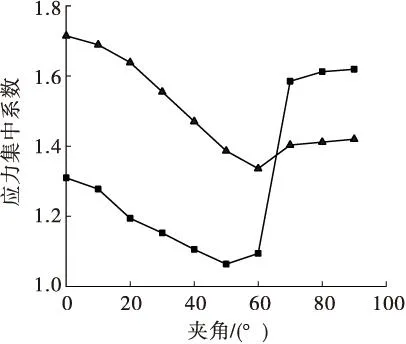
图3　不同夹角下巷道围岩应力集中系数

(1)由图1可得，随着最大水平主应力与巷道轴线夹角的增大,0°～60°底板产生的环向拉应力数值不断减小,受拉区域也持续减小,由连续受拉变为部分受拉,并且在底板呈类似于反拱形，由于拉伸作用使得巷道围岩整体性能降低,在巷道底板产生径向裂隙,造成底鼓破坏；70°～90°底板所受的环向应力逐渐变大,在90°时环向拉应力具有最大值(0.25 MPa)；帮部只在最大水平主应力与巷道轴线平行和垂直时产生径向拉应力,数值分别为0.026 MPa和0.02 MPa；在整个数值模拟过程中顶板没有产生环向拉应力,一直处于受压状态。

(2)分析图2可看出,在整个数值模拟过程中两帮没有产生环向拉应力,顶板也没有产生径向拉应力;底板一直受到径向拉应力作用,这是因为顶板为拱形,有利于降低应力集中,底板为直长边,容易产生较大的应力集中。随着最大水平主应力与巷道轴线夹角的逐渐增大,拉应力先减小后增大,在50°时最小,为0.011 MPa,0°和90°时分别为 0.043和0.042 MPa。

(3)由图3可以看出，顶底板环向应力集中系数随着最大水平主应力与巷道轴线夹角的增大而持续减小。当夹角为50°时,应力集中系数为1.06,随夹角的继续增大到70°时，应力集中系数急剧上升到1.59,在此之后较为稳定,没有出现大幅度增加；两帮环向应力集中系数总体上呈先减小后小幅上升的趋势,在60°时达到最小值为1.34,但垂直时的应力集中系数值小于平行时的应力集中系数值。

综合来看,在σHv型应力场下,巷道围岩的稳定性随着夹角(0°～90°)的改变呈现出复杂的变化；0°～50°时,最小水平主应力对顶底板的环向应力和两帮的径向应力起决定性作用,这时顶底板所受的环向集中应力随着夹角的增大,其影响作用逐渐减小,巷道围岩的稳定性较小夹角时得到了提高；50°～90°时,最大水平主应力在巷道围岩的稳定性中开始逐渐占据主导地位,此时顶底板受到的环向集中应力随着最大水平主应力与巷道轴线夹角的增大开始增大,顶底板的塑性区也随着增大。

2.3.2塑性区

当最大水平主应力与巷道轴线夹角为0°～90°时,塑性区会出现以下几种特征：0°～20°时，帮部的塑性区大于顶底部塑性区,但总体巷道周边塑性区没有出现大的变化;30°～60°时，随着夹角的增加，帮部塑性区呈增大趋势,顶底部塑性区逐渐变小;70°～90°时，帮部以及顶底部塑性区变化情况恰好与30°～60°相反,但底板塑性区要大于顶板塑性区。

2.3.3巷道围岩位移

在巷道顶、底板和两帮中点布置监测点,以确定巷道围岩在最大水平主应力与巷道轴线不同夹角下的收敛量变化情况,根据监测结果绘出围岩收敛量与不同夹角的关系曲线,见图4。

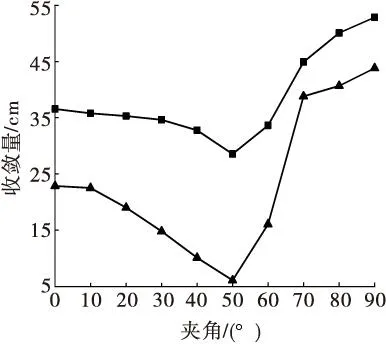
图4　围岩收敛量与不同夹角的关系

整体分析来看, 帮部和顶底板的围岩收敛量随着夹角的增加呈先减小后增大的趋势。当0°～10°时,围岩收敛量变化并不明显;当10°～50°时,巷道周边围岩收敛量持续减小,但帮部收敛量变化速率比顶底板的收敛量变化速率大,这主要是因为原岩水平主应力值逐渐趋近于垂直主应力值,巷道围岩稳定性比其他夹角下的稳定性好，在夹角为50°时巷道围岩收敛量最小,两帮收敛量为6.07 cm,顶底板收敛量为28.55 cm；随着夹角的继续增大,巷道周边围岩收敛量急剧增大，当达到70°～90°时,巷道收敛量增幅减缓,到90°时两帮和顶底板的收敛量分别为43.82，52.86 cm。

从以上分析可知,金川三矿巷道最优布置方式应该是最大水平主应力与巷道轴线成50°附近,这和理论分析的53°最优布置夹角一致。顶底板的收敛变形较两帮严重,在后期建设过程中应加强顶底板支护。

3结论

(1)在σHv型应力场中,巷道的最优布置夹角并不是巷道轴线与最大水平主应力成0°,而是由最大水平主应力、最小水平主应力和垂直主应力三者的大小决定。在本次计算模型中,当巷道轴线与最大水平主应力成53°时,围岩的稳定性最好。

(2)在σHv型应力场中,当夹角小于巷道布置最优夹角时,最小水平主应力对顶底板的环向应力分布起决定性作用；当夹角大于巷道布置最优夹角时,对顶底板环向应力分布起决定性作用的则为最大水平主应力，且顶底板会出现大小相当的环向应力集中,造成巷道底鼓和顶板沉降。

(3)金川公司三矿巷道的变形与破坏主要表现为底鼓与顶板沉降,因此应注重加强巷道顶底板支护。

参考文献

[1]宋志敏,程增庆,张生华.构造应力区软岩巷道围岩变形与控制[J].矿山压力与顶板管理,2005,22(4):48-50.

[2]Kushwaha A, Murali M, Singh S,etal. Effect of in situ horizontal stresses on roadway stability[J].Journal of Mines, Metals and Fuels, 2003,51(3):134-142.

[3]王永才,康红普.金川矿山深井高应力开采潜在的问题[J].中国矿业,2010,9(12):52-55.

[4]鲁岩,邹喜正,刘长友,等.构造应力场中的巷道布置[J].采矿与安全工程学报,2008,25(2):144-149.

[5]倪兴华.地应力研究与应用[M].北京:煤炭工业出版社,2007.

[6]康红普.煤矿井下应力场类型及相互作用分析[J].煤炭学报,2008,33(12):1329-1335.

[7]郑书兵.寺河煤矿三维地应力场分布和巷道布置优化[J].煤炭学报,2010(5):717-722.

[8]张延新,蔡美峰,欧阳振华.地应力与巷道布置关系的理论研究[J].岩土工程技术,2005,19(2):93-97.

[9]张重远,吴满路,廖椿庭.金川三矿地应力测量及应力状态特征研究[J].岩土力学,2013,34(11):3254-3260.

[10]谢文兵,陈晓祥,郑百生.采矿工程问题数值模拟研究与分析[M].徐州:中国矿业大学出版社,2005.

(收稿日期2015-11-01)

Influence of the Maximum Horizontal Principal Stress to the Stability of the Roadway Surrounding Rock

Yan Yongbo1Lu Wen1Zhang Xitao1Wang Junfeng2

(1.School of Environment and Resource, Southwest University of Science & Technology;2.School of Engineering Science,Xichang College)

AbstractBased on the actual measured ground stress of Jinchuan third Mine and a segment roadway,by theoretical analysis method, the optimal placement angle of roadway under the σHv-type stress filed is obtained. Based on FLAC3Dsimulation software,the roadway arrangement is simulated under the condition of the difference angle of maximum horizontal principal stress and roadway axis, besides that,the stress distribution, plastic zone distribution and surrounding rock displacement are conducted contrast analysis. The result show that in the σHvtype stress field, the optimal arrangement of the roadway is forming a certain angle with the maximum horizontal stress; when the angle reaches a certain level,the roof and floor of the roadway will appear the hoop stress, the horizontal stress is the main factor that cause the deformation and destruction of the roadway floor.

KeywordsMaximum horizontal principal stress, Numerical simulation, Surrounding rock displacement

闫永波(1990—),男,硕士研究生,621010 四川省绵阳市涪城区青龙大道中段59号。