傅里叶型平滑结构突变下Dickey-Fuller检验的功效——兼论Shibor的平稳性

张春丽，杨利雄，李庆男

(1.西北民族大学 经济学院 甘肃 兰州 730030；2.兰州大学 管理学院 甘肃 兰州 730000；3.台湾中山大学 经济研究所 台湾 高雄 80611)



傅里叶型平滑结构突变下Dickey-Fuller检验的功效
——兼论Shibor的平稳性

张春丽1，杨利雄2，李庆男3

(1.西北民族大学 经济学院 甘肃 兰州 730030；2.兰州大学 管理学院 甘肃 兰州 730000；3.台湾中山大学 经济研究所 台湾 高雄 80611)

摘要：通过推导Dickey-Fuller检验功效函数，研究表明：即使中小型的傅里叶型结构突变，都会严重影响Dickey-Fuller检验的功效，从而使得含傅里叶型平滑结构突变的平稳过程被误判为单位根过程。使用3、6、9个月期和一年期Shibor日度数据发现：传统的ADF、PP、DF-GLS和KPSS几乎都指出Shibor是单位根过程；考虑平滑结构突变的单位根检验则在1%的显著性水平下拒绝了单位根的原假设，这表明Shibor是含结构突变的平稳过程。因此，预测Shibor和理解其动态行为必须考虑其结构突变特征。

关键词：单位根检验；功效；上海银行间同业拆放利率

一、引言

时间序列的弱平稳性意味着外生冲击造成的影响会随时间减弱，而非平稳性意味着外生冲击造成的影响会永久保留下来；另一方面，平稳时间序列存在均值反转效应，而非平稳时间序列长期值的预测误差会随着时间发散至无穷大，即非平稳意味着长期的不可预测性。因此，理解经济变量的平稳性具有很重要的意义和价值。

单位根检验是甄别时间序列平稳性的主要工具，Dickey 和 Fuller是单位根检验的奠基之作[1]。其后，无论是考虑结构突变的单位根检验或是面板单位根检验都以Dickey-Fuller检验为基础[2-3]。Perron的工作指出了结构突变在检验单位根时的重要性，即传统的单位根检验对含结构突变的平稳过程严重缺乏检验功效(power)[4]。Perron建议通过在结构突变点处加入虚拟变量来解决结构突变问题，并导出了相应的大样本分布。Zivot等其他学者推广了上述理论[5-6]。

Leybourne等将Perron的逻辑反过来使用，阐明了“逆Perron现象”。即，当真实数据生成过程是含结构突变的I(1)序列时，DF检验倾向于虚假地拒绝单位根假设。他们证明：当瞬时突变发生在样本序列的早期时，DF检验错误地拒绝单位根假设的问题十分严重[7]。Leybourne 和Newbold进一步从理论上深入解释了“逆Perron现象”[8]。然而，正如Prodan指出的：正确地估计突变点的个数和突变程度是十分困难的[9]。近来年，Kapetanios、 Becker等认识到：结构突变可能是缓慢发生的、平滑的和非线性的[10-11]。这使得加入虚拟变量捕捉结构突变的能力令人怀疑。

近期有文献采用傅里叶变换来近似结构突变，并且证明单一频率的傅里叶近似能很好地捕捉多种常见的结构突变类型，甚至能很好地捕捉瞬时的(abrupt)结构突变[12]。Enders和 Lee使用傅里叶变换近似结构突变，在Dickey-Fuller框架下，导出了一个考虑结构突变的DF型单位根检验(简称FADF)[12]。因为傅里叶函数近似结构突变的方法不需要假设外生的结构突变点和突变数*另外，Becker等指出傅里叶近似也可以处理非线性趋势[12]。，同时避免了估计结构突变点、突变数和突变程度等问题，也避免了结构突变类型误设问题，这些优势使得该方法十分具有竞争力。本文研究平滑结构突变下，忽略傅里叶型结构突变对Dickey-Fuller单位根检验的影响。

杨利雄等研究了平滑结构突变下Dickey-Fuller检验的大样本行为，证明了忽略平滑结构突变时检验单位根t统计量的渐近分布与Dickey-Fuller一样；同时，使用模拟指出Enders 和 Lee的傅里叶函数扩展型单位根检验(FADF)对含平滑结构突变和瞬时结构突变的时间序列都有理想的小样本性质，而不正确地处理傅里叶型结构突变会扭曲DF单位根检验的小样本性质[13]。

本文的研究从另一方角度证实了傅里叶扩展型单位根检验的优势，即能有效地处理平滑结构突变、甚至瞬时结构突变(abrupt break)，而忽略平滑结构突变对单位根检验的检验功效会产生严重的影响。

彭红枫和鲁维洁、方意和方明等肯定了Shibor(即上海银行间同业拆放利率)作为货币市场基准利率的认可度[14-15]。陈汉鹏和戴金平通过构建DSGE模型研究Shibor作为中国基准利率的可行性，认为央行能够通过Shibor的微调进行货币政策调控[16]。因此，Shibor作为中国短期利率的基准已经得到大致认同。然则，对Shibor平稳性特征的认识还不够深刻。

在本文理论的基础上，研究指出不考虑结构突变的单位根检验会对Shibor的平稳性特征造成误判，从而导致对Shibor特点的错误理解和认识。

二、理论模型

(一)傅里叶函数扩展的DF单位根检验(FADF)简介

假设yt的数据生成过程包含未知结构的依赖于时间的确定性趋势部分α(t)，具体设定如下：

(1-φL)(yt-α(t)-γt)=ut

(1)

其中ut是独立同分布的平稳过程，α(t)是时间的确定性函数。如果α(t)=α0，则式(1)退化为Dickey-Fuller所考虑的数据生成过程[1]。

对于依赖于时间的α(t)，考虑用傅里叶近似来逼近：

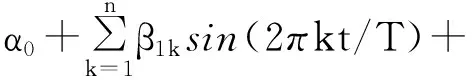
其中，n代表傅里叶近似中包含的频率的个数，k表示频率，T是样本数。Becker等证明单一频率的傅里叶函数就能很好地捕捉常见的结构突变类型[11]。因此，采用单一频率的傅里叶函数近似结构突变：

α(t)=α0+β1sin(2πkt/T)+β2cos(2πkt/T)

(2)

在式(1)和式(2)下，考虑回归模型：

Δyt=ρyt-1+c1+c2t+c3sin(2πkt/T)+c4cos(2πkt/T)+et

(3)

Enders等建议采用OLS估计ρ，其t统计量做单位根检验[12]。这里，t统计量拒绝ρ=0的零假设等价于拒绝式(1)中单位根的零假设φ=1。

Enders等给出了傅里叶扩展型Dickey-Fuller检验(FADF)的相应的临界值，并用模拟指出FADF检验的性质[12]。杨利雄等推导了傅里叶函数扩展型单位根检验的极限分布，并证明了Dickey-Fuller检验的极限分布对平滑结构突变的不变性，同时给出模拟证据表明：FADF甚至对瞬时结构突变也有良好表现[13]。

(二) Dickey-Fuller 单位根检验的检验功效(Power)函数

y-1=α0τ+γt+η

(4)

Δy=γτ+Δη

(5)

另一方面，Dickey-Fuller检验基于回归模型Δyt=ρyt-1+c1+c2t+et中的t统计量：

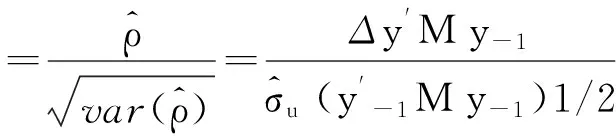
(6)

其中，M=IT-Z(Z′Z)-1Z′,Z=(τ,t)，My=IT-G(G′G)-1G′,G=(τ,t,y-1)，并且τ=(1,1,…,1)′,t=(1,2,…,T)′，y-1=(y0,y1,…,yT-1)′。

B1G′GB1=

基于此，可以证明式(6)右边分母第一项为：

另外，对于式(6)分子项和分母第二项，容易证明：

所以，结合式(6)可得，DF检验的检验功效函数为：

(7)

式(7)即为DF检验的检验功效函数，其是样本和自相关系数φ的函数。

(三) 平滑结构突变下Dickey-Fuller检验的“Perron现象”

考虑平滑结构突变对Dickey-Fuller检验的影响，即平滑结构突变下Dickey-Fuller检验的功效问题。考虑数据生成过程：

(1-φL)(yt-α(t)-γt)=ut

(8)

α(t)=α0+β1sin(2πkt/T)+β2cos(2πkt/T)

(9)

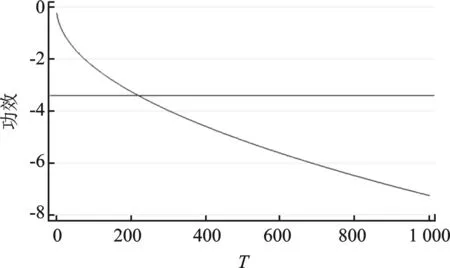
图1　Dickey-Fuller检验的功效与样本的关系(φ=0.9)

y-1=α0τ+γt+β1Υ1,-1+β2Υ2,-1+η

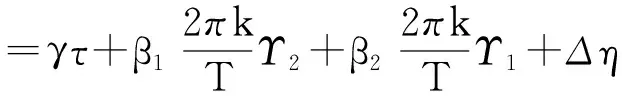
此时使用Dickey-Fuller检验相当于回归方程被误设为：

Δyt=ρyt-1+c1+c2t+et

(10)

式(10)中检验ρ=0的t统计量为：

(11)

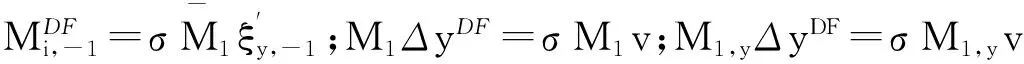
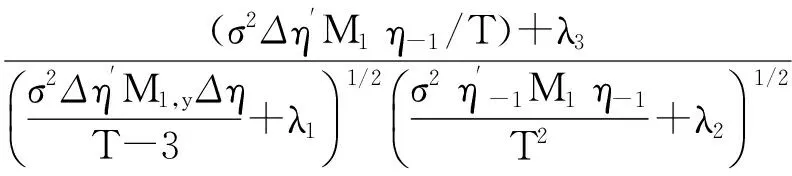
(12)

可以证明：

(13)

(14)

(15)

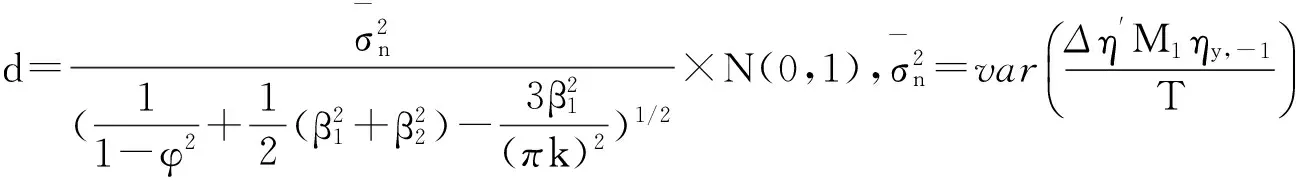
即，当真实数据生成过程(DGP)中包含傅里叶项结构突变，而回归方程错误地没有考虑结构突变时，DF检验的检验功效函数为：

(16)

从式(16)中，不难发现，很小的结构突变就可能严重影响DF检验的功效。为了更直观地理解以上理论结果，图2给出了β1=3,β2=5的数据生成过程下，DF检验的功效与真实DGP中无结构突变情形下DF检验的功效。图2可看出：忽略结构突变的检验几乎完全失去了检验功效，即使当样本达到1 000时，依然无检验功效*包含趋势项的Dickey-Fuller检验5%的临界值为-3.4。。从而使得含傅里叶型平滑结构突变的平稳过程被误判为是单位根过程，即发生了“Perron现象”。

三、实证研究

Shibor的平稳性特征具有重要的政策含义。平稳性意味着外生冲击造成的影响会随时间减弱，而非平稳性意味着外生冲击造成的影响会永久保留下来；另一方面，平稳时间序列存在均值反转效应，而非平稳时间序列长期值的预测误差会随着时间发散至无穷大。本文考虑传统的单位根检验是否会因为未考虑平滑结构而产生对Shibor序列平稳性的误判。

本文选取从2006年10月到2014年10月的3、6、9个月期和一年期Shibor日度数据序列为研究对象，考察Shibor序列的平稳性。图3给出了该序列的3个月期的时间序列图。

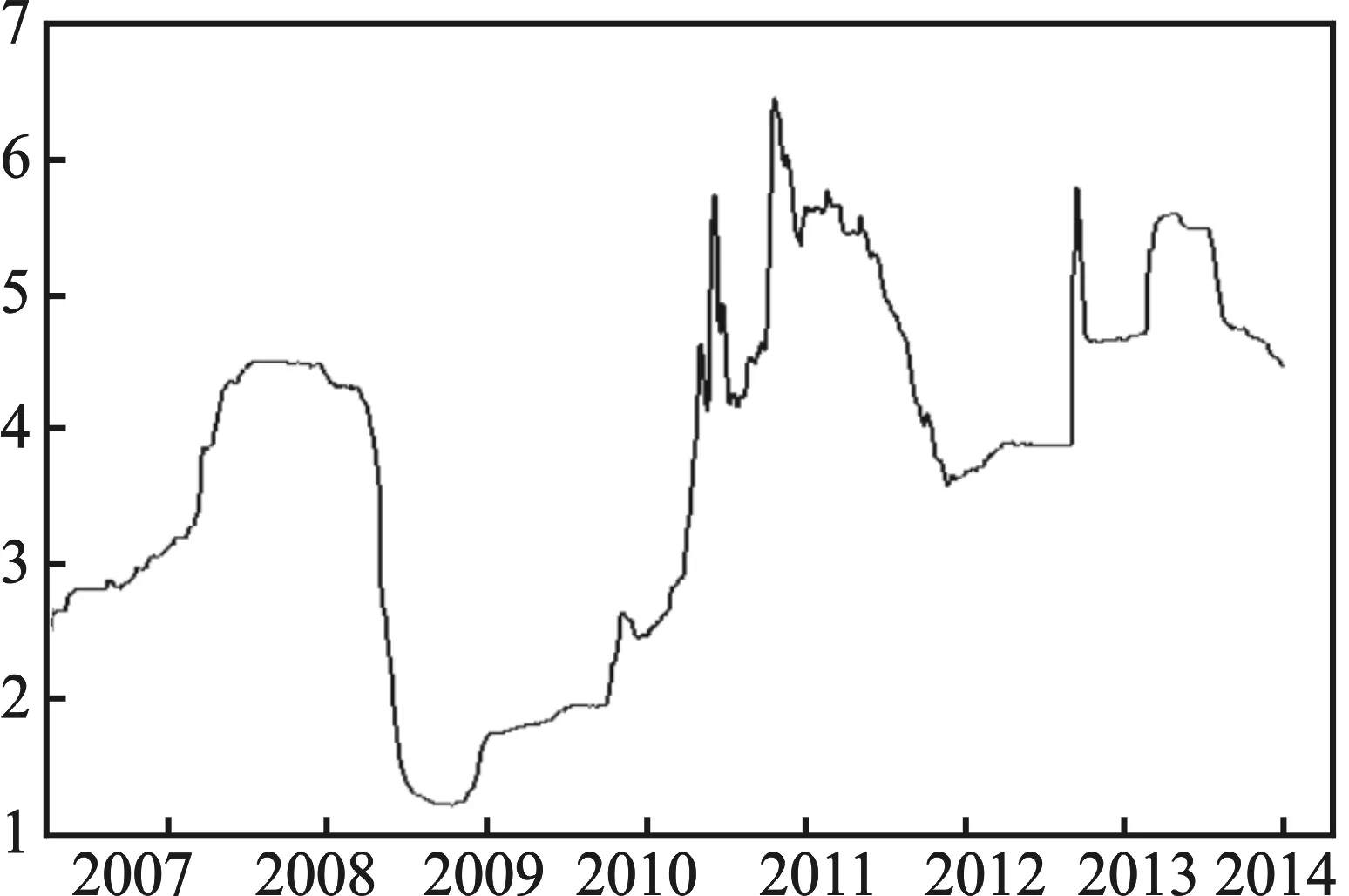
图3　3个月期Shibor序列图

对上述样本使用传统的不考虑结构突变的平稳性检验，其检验结果如表1。从中可以发现：常用的单位根检验，ADF、PP和DF-GLS等检验方法都不能拒绝单位根原假设，从而得出Shibor是单位根过程的结论。KPSS检验在1%的显著性水平下也拒绝了平稳性假设。

表1　Shibor序列的平稳性检验

注：***表示在1%的显著性水平下拒绝了原假设。

表2给出了使用Enders 和 Lee的傅里叶函数扩展型单位根检验结果[12]。在考虑Shibor中的结构突变后，检验该时间序列平稳性。Enders 和 Lee建议：通常情况下，傅里叶变换中的频率从1到5中选择一个拟合程度最高的[12]。本文同时报告频率k=1,2,3,4,5的结果，如表2。使用最小二乘法估计式(3)所示的回归方程式，傅里叶项都在1%的水平下显著，因此考虑平滑结构突变是合理的。从表2的结果中容易发现：考虑Shibor中的平滑结构突变后，在不同结构突变频率下，单位根的原假设在1%的显著性水平下都被拒绝。因此，3个月期Shibor是平稳的。由于“Perron现象”，传统单位根检验方法对含平滑结构突变的平稳过程无检验功效，说明了正确地考虑平滑结构突变的重要性。对于6、9个月期和一年期Shibor日度数据，可以得到类似的结论。因此，常用的检验方法，由于没有考虑结构突变问题，常常引导研究者得到误导性结论：Shibor是不平稳的，也就是将含平滑结构突变的平稳过程误判为单位根过程。

表2　Shibor序列Enders and Lee (2012)傅里叶函数

注：***表示在1%的显著性水平下拒绝了单位根的原假设。

四、总结

Perron阐明了瞬时结构突变对单位根检验的影响，发现瞬时结构突变会严重影响DF检验的功效，并建议使用加入虚拟变量的方式考虑结构突变[4]。但结构突变通常是未知的，而估计结构突变个数和程度十分困难。Becker等、Enders和Lee等建议采用傅里叶变换来捕捉平滑结构突变[11-12]，该方法避开了结构突变个数和程度的估计问题，也可以处理非线性趋势和瞬时结构突变的情形，因此十分有竞争力。

本文先研究了标准Dickey-Fuller检验的性质，即当真实数据生成过程中包含结构突变而被忽略时DF检验的功效。理论表明：即使忽略比较小的傅里叶型平滑结构突变，其对检验功效的影响也是十分大的。

以中国2006年10月到2014年10月的3、6、9个月期和一年期Shibor日度序列为研究对象，实证发现：通常的平稳性检验方法如ADF、PP、KPSS和DF-GLS会给出Shibor包含单位根的结论；而使用考虑结构突变的傅里叶函数扩展型单位根检验，则在1%的显著性水平下，可以拒绝存在单位根的原假设，即本文的研究表明：Shibor是含结构突变的平稳过程。因此，预测和理解Shibor的动态行为必须建立在合理考虑结构突变的基础上。

参考文献：

[1]Dickey D A, W A Fuller. Distribution of the Estimators for Autoregressive Time Series with a Unit Root [J]. Journal of the American statistical association, 1979, 74(366).

[2]江海峰,崔立志,汪忠志. 递归均值调整单位根检验能提高检验功效吗?[J]. 统计与信息论坛,2014,29(11).

[3]江海峰,陶长琪,陈启明. ADF模式中漂移项和趋势项检验量分布与Bootstrap检验研究[J]. 统计与信息论坛,2014,29(6).

[4]Perron P. The Great Crash, the Oil Price Shock, and the Unit Root Hypothesis [J], Econometrica, 1989,57(6).

[5]Zivot E, W K D, Andrews. Further Evidence on the Great Crash, the Oil Price Shock and the Unit Root Hypothesis [J]. Journal of Business and economics statistics, 1992, 20(1).

[6]Lumsdaine R L, Papell D H. Multiple Trend Breaks and the Unit Root Hypothesis [J]. The review of economics and statistics, 1997, 79(1).

[7]Leybourne S J, C Mills T, Newbold P. Spurious Rejections by Dickey-Fuller Tests in the Presence of a Break Under the Null[J]. Journal of Econometrics, 1998, 87(1).

[8]Leybourne S J, Newbold P. Behaviour of the Standard and Symmetric Dickey-Fuller‐Type Tests When There is a Break Under the Null Hypothesis[J]. The Econometrics Journal, 2000, 3(1).

[9]Prodan R, Potential Pitfalls in Determining Multiple Structural Changes With an Application to Purchasing Power Parity [J].Journal of Business and economics statistics, 2008, 26(2).

[10]Kapetanios G, Shin Y, Snell A. Testing for a Unit Root in the Nonlinear STAR Framework[J]. Journal of Econometrics, 2003, 112(2).

[11]Becker R, Enders W, Lee J. A stationary Test in the Presence of an Unknown Number of Smooth Breaks [J]. Journal of Time Series Analysis, 2006, 27(1).

[12]Enders W, Lee J. The Flexible Fourier Form and Dickey-Fuller Type Unit Root Tests [J]. Economics Letters, 2012, 117(2).

[13]杨利雄，张春丽，李庆男. 平滑结构突变下Dickey-Fuller检验的大样本行为[J]. 统计研究, 2013(11).

[14]彭红枫,鲁维洁. 中国金融市场基准利率的选择研究[J]. 管理世界,2010(11).

[15]方意,方明. 中国货币市场基准利率的确立及其动态关系研究[J]. 金融研究,2012(7).

[16]陈汉鹏，戴金平.Shibor作为中国基准利率的可行性研究[J]. 管理世界, 2014(10).

(责任编辑：张爱婷)

The Power of Dickey-Fuller Test and the Stationarity of Shibor under the Fourier-form Smooth Breaks

ZHANG Chun-li1， YANG Li-xiong2， LI Qing-nan3

(1. School of Economics, Northwest University for Nationalities, Lanzhou 730030, China;2.School of Management, Lanzhou University, Lanzhou 730000, China；3.Insititute of Economics, National Sun Yat-sen University, Taiwan 80611, China)

Abstract:By deriving the power function of Dickey-Fuller test, we show that even a small or medium break can dramatically deteriorate the power of DF test, hence lead to the conclusion that a stationary process with a smooth break is mistaken as a unit root process. Based on the daily data of Shibor with the periods of 3, 6, 9 and 12 months, the empirical results show that the traditional tests such as ADF, PP, DF-GLS and KPSS all tend to indicate the nonstationarity of Shibor, but the Fourier-augmented Dickey-Fuller test can reject the unit root null at the 1% significant level. This shows that Shibor is stationary with breaks. Therefore, it is necessary to concern the structural breaks in forecasting and understanding the dynamics of Shibor.

Key words:unit root test; power; Shanghai interbank offered rate (Shibor)

收稿日期：2015-09-25；修复日期：2015-12-20

基金项目：中央高校基本科研业务费专项资金项目《考虑结构突变的计量预测方法及其应用》( 31920150119)

作者简介：张春丽，女，河南焦作人，助教，研究方向为：金融市场、时间序列分析；

中图分类号：C812

文献标志码：A

文章编号：1007-3116(2016)05-0021-06

杨利雄，男，甘肃陇南人，经济学博士，讲师，研究方向:金融市场、时间序列分析；

李庆男，男，台湾高雄人，经济学博士，教授，研究方向:计量经济学。

【统计理论与方法】