高三复习课变式教学的设计与反思
——以“函数与方程思想在不等式中的应用”一课为例
2016-06-01◎李影
◎李 影
(江苏省南通大学附属中学,江苏 南通 226000)
高三复习课变式教学的设计与反思
——以“函数与方程思想在不等式中的应用”一课为例
◎李 影
(江苏省南通大学附属中学,江苏 南通 226000)
通过变式教学的深度学习训练,进行自主建构,才能对数学学习提升兴趣,达到二轮复习数学的目的、意义.
变式教学;函数与方程;恒成立;有解
高三数学专题复习若能形成知识串、变式训练题串,可提高复习效率,使学生掌握更系统连贯的知识体系,便于从高层次、深内涵上去理解知识点,拓宽学生视野.二轮复习是在学生拥有了完整的知识网络下,希望通过二轮复习能站在更高起点上认识本质,优化解决方法,提高思维能力,强化探索内化知识的能力,促进整体能力的一个提升.
一、课堂教学简录
引入:关于x的方程x2+ax-1=0,x∈[1,2]上有解,求实数a的取值范围.

老师:非常好.学生1把此题貌似与函数不相关的问题用函数思想把a看成关于x的函数,从表象看到问题本质,从函数值域入手解决开阔了视野,沟通已知与未知的关系,找到解决问题的思路.学生2把一元二次方程在某区间有解问题转化为根的分布问题,思维开阔缜密.两个同学各自从不同角度阐述了这类问题的解答,说明同学思想有一定的深度,能挖掘问题的本质,进而找到问题的切入口,纵观这类问题,a=f(x)在x∈D上有解,则a的取值范围即f(x)的值域(x∈D),从一个侧面说明函数与方程是解决数学问题的重要思维线索.
变式1 关于x的不等式x2+ax-1<0,x∈[1,2]上有解,求实数a的取值范围.
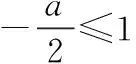
变式2 关于x的不等式x2+ax-1<0,x∈[1,2]上恒成立,求实数a的取值范围.
感悟反思:不同的切入点将我们带入数学多角度解题的宽径,在多种方法中比较最优化的方法,感受数学美之魅力所在.
总结:a>f(x)有解⟺a>f(x)恒成立.
二、教学设计反思
1.本文以最简单的题目形式呈现,以变式题目展示不同背景,凸显函数的图像、值域等性质在解题中的作用,采用分离参变量、数形结合、一元二次方程根的分布知识或思想方法.通过这节课的教学,学生充分感受到数学符号语言的丰富内涵.
2.不足或改进:课时紧,容量有限,应该把二次背景(方程、函数)拓展为非二次背景.
数学教学应着重多种变式教学,精心挑选问题,重组问题,演变问题,使数学各分支有效系统地重组,达到知识融会贯通.本文引导学生有效理解了以不变应万变的常规解题途径和思维优化的方法,提高高三复习课学生的思维品质,增强学好数学的信心.
三、感 悟
通过变式题的拓展训练,多种策略、综合运用、比较优化,创造了利用函数图像这一有效工具的视点,帮助学生在解决问题中系统地理解和掌握数形结合给解题带来的省时省力的变化.变式教学变换问题的形式,不改变问题的本质,思想变,方法变,脱去伪装外衣,抓本质,找到原型,找到基本方法,促进学生数学的核心素养提升.通过变式教学的深度学习训练,进行自主建构,才能对数学学习提升兴趣,达到二轮复习数学的目的、意义.
本文系2016年南通市教研课题“高中数学复习课‘问题解决’课堂教学模式的研究与实践”的中期成果.
