两类分布式优化问题关系初探

刘长有 李 磊

(1.泰山学院后勤产业管理处，山东 泰安 271016； 2.泰山医学院管理学院，山东 泰安 271000)



两类分布式优化问题关系初探

刘长有1李 磊2

(1.泰山学院后勤产业管理处，山东 泰安 271016； 2.泰山医学院管理学院，山东 泰安 271000)

讨论了两类重要的分布式优化问题之间的关系，给出了这两类分布式优化问题的数学表达，并利用拉格朗日对偶原理得出了它们的关系，即一类问题可以表示为另一类问题的对偶问题。

凸优化，分布式，对偶优化

随着复杂大系统和大型网络的兴起，分布式优化也在很多领域中起着越来越重要的作用。比如在分布式模型预测控制、分布式信号处理等领域，分布式优化都起着很重要的作用[1]。分布式优化中有两类非常重要的问题：在第一类分布式优化问题中，每个智能体都有自己的目标函数和约束集合，并且每个智能体并不知道其他智能体的目标函数和约束集合。但是，所有的智能体却有着公共的优化变量[2]。我们称这类优化问题为Ⅰ类分布式优化问题。在另一类分布式优化问题中，每个智能体都有自己的目标函数、约束集合和优化变量，并且每个智能体并不知道其他智能体的目标函数。但是，这些智能体之间的约束集合并不是相互独立的，它们的约束集合是相互影响的。我们称这类分布式优化问题为Ⅱ类分布式优化问题。这两类分布式优化问题在现实中有着非常重要的应用，学者也为这两类优化问题设计出了种种不同的算法。在这样的背景下，探讨这两类问题之间的关系就显得非常重要，因为弄清楚了它们之间的相互关系后，我们可以根据它们之间的关系设计更加有效的算法来解这两类分布式优化问题。本文的探讨表明这两类分布式优化问题有着非常深刻而重要的联系：Ⅱ类分布式优化问题的拉格朗日对偶问题是Ⅰ类分布式优化问题。

1 预备知识

在本节中，我们介绍凸优化和拉格朗日对偶优化的相关知识。

1.1 凸优化

集合C是凸集，如果∀x,y∈C,αx+(1-α)y∈C，∀α∈[0,1],亦即，以C中任意两点为端点的线段也在C中。函数f是凸函数，如果它的定义域D是凸集，并且满足如下条件:

f(αx+(1-α)y)≤αf(x)+(1-α)f(y),∀α∈[0,1],∀x,y∈D。

每个凸函数在它定义域的内部都是连续函数。

一个优化问题是凸优化问题，如果它的目标函数和约束集合都是凸的，亦即有如下问题:

subject to x∈X。

该问题是凸优化问题，如果f(x)是凸函数，并且x是凸集合。

当优化问题表示为如下形式时：

(1)

它是一个凸优化问题，如果fi(x)(i=0，1，…,m)是凸函数而且hj(x)(j=1,…，p)是线性函数。

1.2 对偶优化问题

在这一部分，我们介绍如何得到凸优化问题(1)的对偶问题。

首先，问题(1)的拉格朗日函数为:

对该拉格朗日函数取关于x的最小值，我们得到问题(1)的拉格朗日对偶函数:

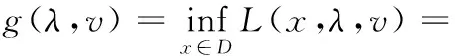
其中，D为fi(x)(i=0，1，…,m)和hj(x)(j=1,…，p)的公共定义域；g(λ,v)为关于(λ,v)的凹函数。

那么，优化问题(1)的拉格朗日对偶问题如下：

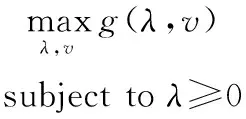
(2)

对于拉格朗日对偶问题(2)，我们有如下引理：

引理1：拉格朗日对偶问题(2)是一个凸优化问题。

令p*为原优化问题(1)的最优值，d*为对偶问题(2)的最优值。则弱对偶d*≤p*始终成立。而强对偶d*=p*在一定条件下成立。对于强对偶，我们有如下引理：

引理2(Slater’s Condition):如果存在点x使得下式成立:

fi(x)<0i=1,…，m,

hi(x)=0i=1,…，p。

则当优化问题(1)是凸优化问题时，强对偶d*=p*成立。

2 分布式优化

本节中，我们介绍两类分布式优化问题。首先我们介绍Ⅰ类分布式优化问题。

2.1 Ⅰ类分布式优化问题

在该类问题中，每个智能体都有自己的目标函数和约束集合，但是所有的智能体共享公共的优化变量。在数学上，该类问题可以表示如下：

(3)

其中，fi(i=1,…,n)为每个智能体自己的目标函数；Xi(i=1,…，n)为每个智能体自己的约束集合；全局约束集合X为所有Xi(i=1,…，n)的交集。在Ⅰ类分布式优化问题(3)中，所有智能体共享公共的优化变量x。

2.2 Ⅱ类分布式优化问题

在该类问题中，每个智能体都有自己的目标函数和优化变量，但是不同智能体的约束集合却是相互影响的。在本文中，我们只讨论带有线性等式和线性不等式约束的Ⅱ类分布式优化问题。其在数学上可以表示为：

(4)

其中，fi(i=1,…,n)为每个智能体自己的目标函数；xi(i=1,…，n)为每个智能体自己的优化变量；x=(x1,…，xn)为所有智能体优化变量。我们看到，在Ⅱ类分布式优化问题(4)中，不同智能体之间的约束是以加法的形式相互影响的。

3 两类分布式优化问题的关系

在本节，我们通过拉格朗日对偶优化原理，得出Ⅱ类分布式优化问题(4)可以通过拉格朗日对偶方法转化为Ⅰ类分布式优化问题(1)。

首先，Ⅱ类分布式优化问题(4)的拉格朗日函数为:

其中v,λ均为问题(4)的对偶变量；上标T为转置。

为对该拉格朗日含对求关于xi的最小值，我们令:

那么将xi代入上面的拉格朗日函数，我们得到:

则问题(4)的对偶问题为：

maxg(v,λ)

subject toλ≥0。

我们得到Ⅱ类分布式优化问题(4)的对偶问题为:

(5)

我们看到，问题(5)实际上是Ⅰ类分布式优化问题(3)的一个特殊形式。当Ⅱ类分布式优化问题(4)满足引理2中的Slater’s Condition时，强对偶成立。这是我们可以从问题(5)的最优解得到问题(4)的最优解。所以，我们可以通过拉格朗日对偶方法，将Ⅱ类分布式优化问题(4)转化为其拉格朗日对偶问题来解，而问题(4)的拉格朗日对偶问题恰好是Ⅰ类分布式优化问题(3)的一种特殊形式。

4 结语

我们探讨了两类重要的分布式优化问题的关系。我们利用拉格朗日对偶优化原理，得出Ⅱ类分布式优化问题可以通过对偶原理转化为Ⅰ类分布式优化问题。

[1] J.Mota,J.Xavier,P.Aguiar,et al.Distributed optimization with local domains:Applications in mpc and network flows[J].Automatic Control,2015,60(7):2004-2009.

[2] A.D’Amico,L.Sanguinetti,D.Palomar.Convex separable problems with linear constraints in signal processing and communications[J].Signal Processing,2014,62(22):6045-6058.

On relationship of two distribution optimization

Liu Changyou1Li Lei2

(1.Logistics Industrial Management Office, Taishan College, Tai’an 271016, China;2.School of Management, Taishan Medical University, Tai’an 271000, China)

The paper discusses the relationship between the two important distributions optimization, provides the mathematical expression for the two distribution optimization, and concludes their relationship by using Lagrangian duality principle, so the kind of problem can be expressed as the duality of the other problem.

convex optimization, distribution, duality optimization

1009-6825(2016)34-0257-02

2016-09-21

刘长有(1980- )，男，助理工程师； 李 磊(1981- )，女，讲师

O224

A