The heat transfer optimization of conical fin by shape modification

Jiansheng Wang,Xiao Wang

Key Laboratory of Efficient Utilization of Low and Medium Grade Energy,MOE,School of Mechanical Engineering,Tianjin University,Tianjin 300072,China

1.Introduction

Since fins are widely used in thermal engineering field such as heat exchanger,air conditioning as well as some other heat transfer process,more and more attentions have been paid on the fin optimization[1].So far most optimizations of the fin or fin arrays have been carried out by theoretical analysis or numerical simulation,which focused on the geometry parameters or the performance of fin or fin arrays.

Adrian and Almogbel[2]studied the relationship between the geometry of T-shaped assemblies and the global thermal conductance,and obtained the optimum value of the latter one.Kundu and Das[3]investigated the optimization of fin arrays and found that the supporting structure and the convection had a significant influence on the performance of fin array.Lorenzini and Rocha[4]studied the optimum geometry of a T-Y fin with numerical method and obtained the minimum thermal resistance of the assembly.Kundu and Bhanja[5]proposed a model of thermal performance and optimization to investigate the influence of geometric and thermal parameters on the fin performance and optimization result.The results indicated that the fin performance obtained by the model was lower,and the optimum heat transfer rate was higher compared with that of the previous results.Zhang and Liu[6]probed the optimal spacing between the isothermal laminar natural convection plates to obtain the best heat transfer performance with theoretical analysis and numerical simulation.Kundu and Barman[7]studied wet annular fin assemblies of the trapezoidal pro file and performed the optimum design of the fin.They found that both the psychrometric properties of air and selected approach had an influence on the performance of a wet fin assembly.Kundu and Le[8]studied the optimum fin geometric shape for minimizing fin volume.The process was carried out under the condition of the certain heat transfer rate.Feng and Li[9]optimized the structure parameter of circler fin for optimum fin efficiency through numerical simulation.

As mentioned above,the vast majority of the optimization processes were performed within a limited scale,which could only be turned out to obtain optimalresults locally.In order to find the optimalresultin the range of full-scale,various genetic algorithms(GA for short)have been applied in the optimization problems.GA can prevent focusing on a local solution by searching multiple areas in solution space simultaneously[10].

Copiello and Fabbri[11]investigated the optimization of wavy fins with multi-objective genetic algorithm.Azarkishet al.[12]investigated the optimization of fin arrays,the optimum fin pro file and the number of fins in the array were obtained with a Modified genetic algorithm.Azarkishet al.[13]studied the geometric optimization of a longitudinal fin with volumetric heatgeneration by applying the B-spline curves and the genetic algorithm.The results showed that the fin efficiency decreased with the increase of the base temperature and the volumetric heatgeneration.Wang and Heetal.[14]coupled genetic algorithm(GA)with numerical simulation to optimize the con figuration of a twodimensional slotted fin.Das[15]studied the optimization of an inverse problem with genetic algorithm to optimize some properties and parameters of cylindrical fin which satisfies a given temperature distribution.Hajabdollahiet al.[1]investigated the optimal geometry of a pin fin,which was determined by Bezier curves.The total heat transfer quantity and fin efficiency were chosen as objective functions.Iqbalet al.[16]investigated the optimum shape of longitudinal fins for maximizing the Nusselt number with genetic algorithm.The result showed that the Nusselt number increased effectively.Moon and Kim[17]studied the heat transfer performance of a new fan-shaped pin- fin in a rectangular channel through hybrid evolutionary algorithm and compared its performance with that of a circular pin- fin.The results showed that the averaged Nusselt number of the fan-shaped pin- fin was obviously superior to that of the circular pin- fin in the whole considered range of Reynolds number.Ryu and Yook[18]optimized the performance of a corrugated louvered fin through the Kriging method and micro-genetic algorithm and obviously improvement in the performance of the corrugated louvered fin was obtained.

In general,the optimization of the fin by genetic algorithm is relatively mature.It can be noticed that most of optimizations of the fin geometry have been performed by assuming the pro file of the fin such as polynomial curves or Bezier curve.The assumed pro file is more or less subjective,which wouldn't lead to the real optimum result.To obtain general optimum geometry of the fin,a new method which is based on the stepping construction with genetic algorithm is proposed in present work.Furthermore,in order to explain the performance of the new optimization algorithm,the conical fin has been chosen as the initial model for optimization and compared with the performance of the optimum fin in the literature[1].

2.Problem Description

The sketch of the conical fin with variable section is shown in Fig.1(a).

In order to find the heat transfer rate,the fin is divided into limited differential elements in the longitudinal(x)direction.Every element is treated as a part of conical fin which is composed of elemental conical fins with respective generatrix slope.Each element is connected to the next one,in addition to the element connected to the base structure,the temperature at the base of differential element equals to that at the lower one top.The temperature at the base of first differential element of the fin is a constant ofTb[as shown in Fig.1(a)].

To simplify the numericalcomputation process and obtain reasonable results,some assumptions are made as follows.

The one-dimensional approximation can be employed in heat conduction of the fin under the following condition,[19,20]

whereAis the cross-sectional area of the fin,Pis the circumferential perimeter of the fin,δ is the characteristic thickness of the fin,which is taken to be the diameterDfor cylindrical ones.

The above equation means that the conduction thermal resistance in the transverse direction is much less than the convection thermal resistance of the fin surface,which result in the fin temperature varies in one direction only(longitudinal(x)direction)and the temperature variation along the transverse direction is negligible.Therefore,the heat conduction in the transverse direction is negligible,and studies have shown that the error involved in one-dimensional fin analysis is less than about 1%[20].

In present work,with the thermophysical parameters of used materialof the fin and other boundary conditions(shown in Section 5.2),the maximum of Eq.(1)can be obtained as follows,

So,the above results indicate that the heat conduction in present conical fin can be treated as one-dimensional.By the way,no heat generation exists in present considered fin.

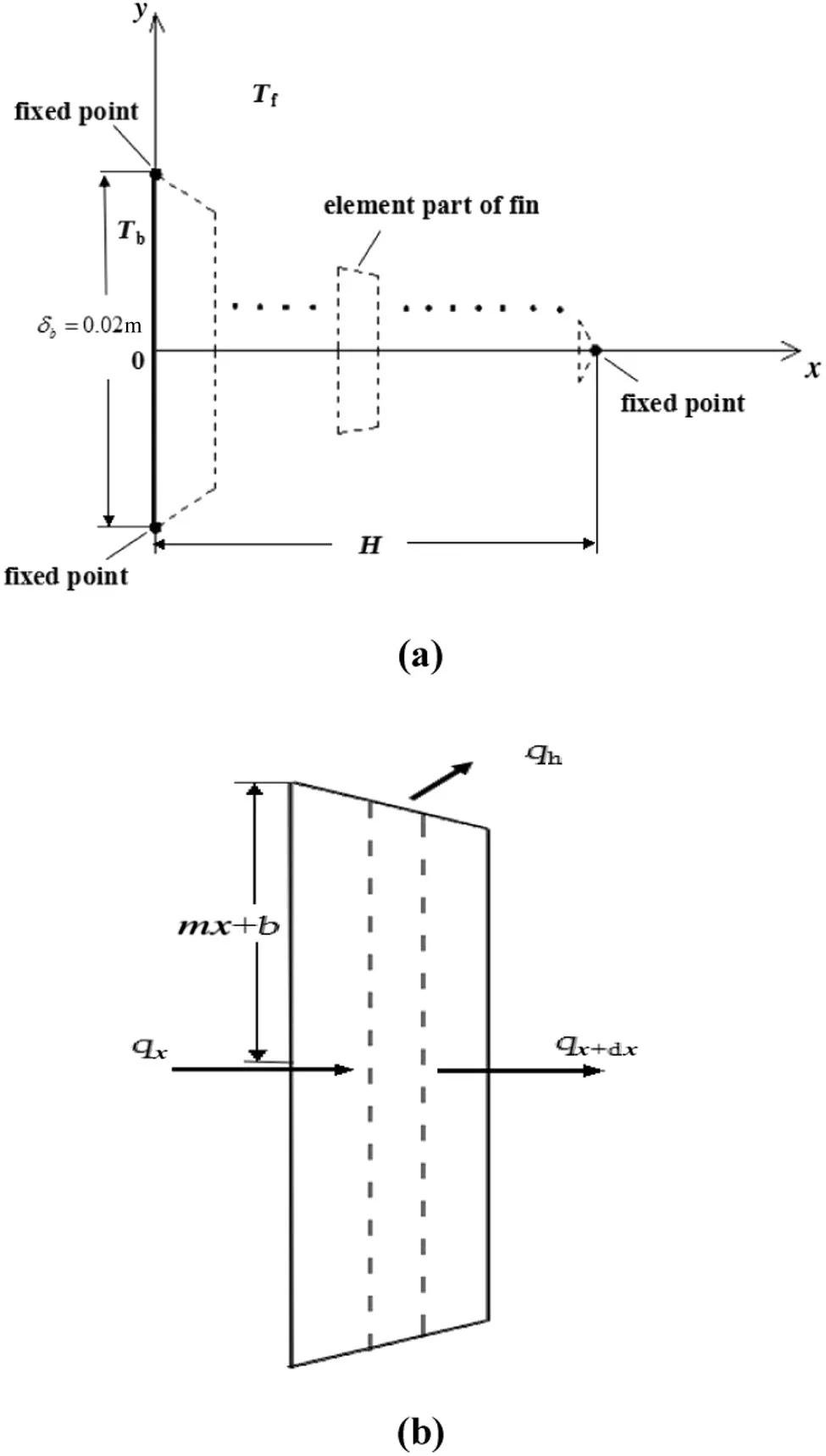
Fig.1.(a)The sketch of fin dividing.(b)Energy balances of differential element.

Based on the energy conservation of conic element of fin as shown in Fig.1(b),the following equation can be obtained,

whereqxis the heat conduction rate inxposition,andqhis the convection heat transfer rate from the fin surface to surrounding environment of conical element.

From Fourier's law,it can be obtained,

whereAcsis the cross-sectional area of conical element,which varies with the heightxof the fin.Since the conduction heatrate at the locationx+dxmay be expressed as,

It follows that

The convection heat transfer rate may be expressed as,

wherekis the thermal conductivity of the fin,his the convective heat transfer coefficient of the fin surface,Asis the surface area of the differential conical element.

The generatrix of differential element of fin is assumed to be a straight line with slopemand interceptb.Therefore,AcsandAsmay be expressed as the following respectively,

By solving Eq.(2),we obtain differential equation of heatconduction

To solve Eqs.(9)or(10),the boundary conditions of each differential element are given as follows,

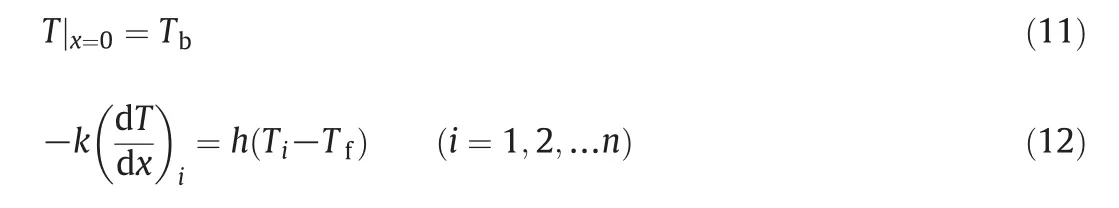
whereiis the number of differential element of fin under optimization.To obtain the optimum geometry of fin,a stepping optimization method is proposed in present work,which will be explained in details in the following section.

3.Stepping Genetic Algorithm Optimization

3.1.Stepping genetic algorithm

The GA(genetic algorithm)is semi-stochastic methods,which is based on Darwin's laws of natural selection[1].Referring to the mechanism of building construction,the stepping genetic algorithm is proposed.Every differential element optimization begins after the below one has been constructed.By the way,the process of constructing the geometry of fin by optimum result of each differential element will be discussed in Section 3.4.Consequently,every differential element of conical fin will be connected to each other to form the final optimum fin.It's expected that the optimum result of each differential element can be obtained in terms of the optimum results of the whole fin(Fig.1a),and the construction process will be finished until the top differential element has been optimized.

3.2.Genetic options

In genetic algorithm,operators-selection,crossover and mutation are three main factors.Selection is the process of choosing the better individuals based on the fitness to form a new population.Highly fitted individuals,relative to the whole population,have more chance to be selected as parents in next generation[21].

Crossover is also known as recombination,which imitates the process of two homologous chromosomes'recombinationviamating to form new chromosome.And crossover rate ranges from 0.4 to 0.99.In present work,0.7 is selected as the crossover rate and will be discussed later.

Taking one-point crossover as an example,as shown in Fig.2(‘|’represents the crossover point),according to the crossover rate,two individuals will exchange part of the chromosome at the crossover point thus form two new individuals.

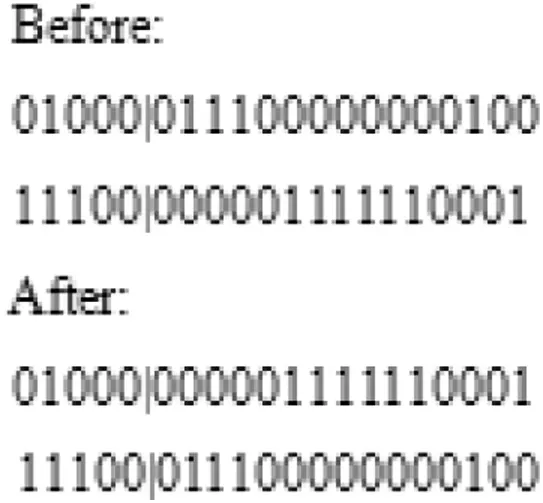
Fig.2.One-point crossover.

Mutation is to make changes in one or more parts of the chromosome with small probability.The purpose of mutation is to introduce occasional perturbations into the parameters to maintain genetic diversity within the population[22].For example,as shown in Fig.3 with binary code,mutation means ‘0’to ‘1’or ‘1’to ‘0’to form new individuals.The mutation rate ranges from 0.0001 to 0.1.In present work,0.035 is selected as the mutation rate.

Fig.3.Mutation.

3.3.Objective function

In present work,the total heat transfer rate from the fin surface to surrounding fluid is treated as the objective function,which can be described as follows,

During the optimization process,the fin efficiency is traced simultaneously,which can be described as follows,

where As0represents the to talsurface area of fin.In presentwork,we try to find the maximumvalue of the objective function,thus to find out the general optimum geometry parameters of the fin.

3.4.Theoretical feasibility of stepping genetic algorithms

According to the previous available literature[13-18,21,22],the genetic algorithm has been widely used in various kinds of fin optimization scheme,which has been proved to be an effective and feasible method for optimization.In order to make it applicable to present case,some key parameters(such as crossover probability)have been investigated,which will be introduced in the following sections.

In terms of the proposed stepping method,modifying the optimization process to conform the realcondition of the fin and guaranteeing to obtain the optimum heat transfer rate of the whole fin are key steps of the present optimization.So,in the optimization process,the element next to the base of the fin is treated as the first differential element and optimized under the convective heat transfer boundary condition.With the genetic algorithm,the first differential element geometric parametersm1andb1determined by the temporary optimum total heat transfer rate(derived from Eq.(10)and(13))can be obtained.Then,on the basis of the first optimum differential element,the second one(geometric parameters ism2andb2,respectively)will be applied to the first differential element.The new element which consists of the two differential elements will be optimized as a temporary whole rather than separate one in the new optimization.In order to complete the optimization process,a certain curve(conic generatrix)is fitted through two different elements,then the new heat diffusion equation of the first two combined differential elements could be solved as solving of first element.Then the optimum parameterm2andb2will be con firmed finally based on the temporary optimum total heat transfer rate.In this way,the optimization procedure will continue along the longitudinal(x)of fin until reaching the top of the fin.

In a word,the stepping genetic algorithm proposed in present work conforms to physics law based on the real condition,which could guarantee the reliability of the optimization results as well.

4.Solution Procedure

The fin is divided into some elements,which connected to each other.The genetic algorithm is used to evaluate the parametersmas well asband export them to the objective function.Total heat transfer rate and fin efficiency are evaluated at every optimization process,then the optimized data is returned back to the genetic algorithm to process the optimization.

In addition,it should be noticed that the optimum geometry of the conical fin includes two types(as shown in Fig.4(a)and(b))according to the principle of heat transfer.In present work,the total heat transfer rate from the fin surface to surrounding fluid is selected as the objective function,so the final geometry of the optimum conical fin would be similar to that in Fig.4(a).As a result,during the optimization process,the slope control of differential element in every step of optimization will be applied to ensure that a regular geometry of the optimum fin can be obtained.The solution procedure of genetic algorithm is shown in Fig.5.

5.Results and Discussion

The optimization results of the conical fin,selection of the genetic algorithm parameters and the error analysis of the obtained results are discussed in this section.Furthermore,the optimum geometry as well as the performance of the fin based on the objective function of maximum total heat transfer rate is analyzed as well.

5.1.Selection of genetic algorithm parameters

In order to obtain more accurate results of the estimated parameters,it is essential to investigate the effect of some relative parameters of genetic algorithm on the result.

Fig.4.Two kinds of optimum geometry.

The optimization result of the first differential element of the conical fin is shown in Fig.6.It's obvious that 100 generations are sufficient enough to obtain solution of maximizing the objective function.So,in the next step of genetic algorithm optimization process,to be more economic,60 is chosen as the maximum number of generations.Based on the crossover and mutation rate,some combinations are shown in Table 1.

As shown in Table 1,according to the crossover probability,for all kinds ofPm,the objective function more likely have the maximum value whenPc=0.7,thusPc=0.7 is selected in optimization.Similarly,according to the mutation probability,the objective function are more likely have the maximum value whenPm=0.035 andPm=0.035 is chosen as mutation rate.

5.2.Case study

In present case,the parameters of the conical fin are assumed as follows,

·thermal conductivity,k=180 W⋅m-1⋅K-1,

·convective heat transfer coefficient,h=20 W⋅m-2⋅K-1,

·base temperature,Tb=500 K,

· fin height,H=0.24 m,

Fig.5.The algorithm of solution procedure.

·base cross-section diameter,δb=0.02 m,

·terminal cross-section diameter,δt=0 m,

·ambient fluid temperatureTf=300 K.

As mentioned above,the parameters setup for the genetic algorithm used to optimize the conical fin is as follows,

·population size,N=100,

·maximum number of generation,NIND=60,

·crossover probability,Pc=0.7,

·mutation probability,Pm=0.035.

Fig.6.The optimization result of the first differential element conical fin.

The result of the optimization is shown in Fig.7,which has shown about the two-dimensional projection of half part of the optimized conical fin geometry along the symmetric axis direction.And the total heat transfer rate of the conical fin is treated as the objective function in Fig.7.In the process of optimization,the conical fin is divided into 20 differential elements(will be discussed later).The optimization results of the conical fin are shown in Table 2.By the way,the total surface area and total volume of the conical fin are the sum of each optimized differential element.The total fin efficiency is obtained from Eq.(14).

Compared the present optimization results with that of Paretooptimal[1].It can be found that the maximum total heat transfer rate]increases by 6.5%with stepping method proposed in present work.Meanwhile,the total volume of the conical fin increases by 3.8%,and the fin efficient decreases by 2.6%.In stepping optimization method,the augment of maximum total heat transfer rate is more than the reduction of the fin efficiency.So,it can be drawn a conclusion that the stepping method proposed in present work could obtain more satisfactory optimization results.

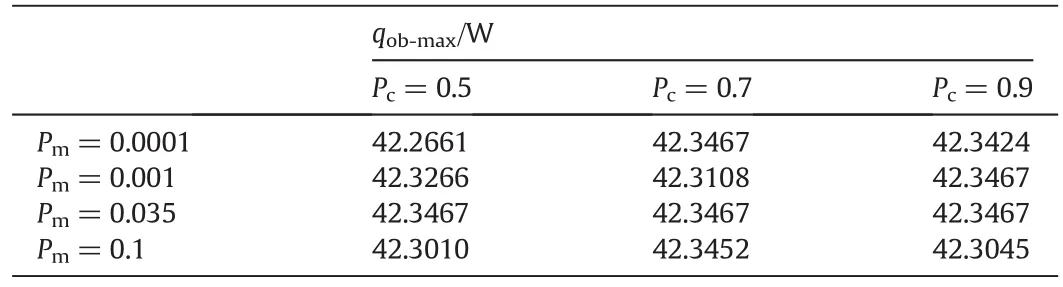
Table 1Selection of crossover and mutation rate

Fig.7.The optimized conical fin geometry.

Table 2The optimum results of the conical fin obtained by the present work and the literature[1

To illustrate advantage of the stepping method,the performance parameter of the conical fin in present work,the result of rectangular fin,triangular fin as well as pin fin(with the same physical parameter)have been listed in Table 3.

Table 3The performance parameter of the conical fin in present work,rectangular fin,triangular fin and pin fin

As shown in Table 3,it's found that triangular fin has minimum volume of three fins.Based on the criterion of total heat transfer rate and fin efficiency,the conical fin gained with present optimization method has obvious predominance.So,it may be drawn a conclusion that the stepping genetic algorithm is effective in optimizing.

5.3.Error analysis

5.3.1.Error from fin dividing

In order to probe the optimization in more details,the fin is divided into some differential elements.To obtain more accurate results,the influence of differential element number on the result is investigated.The number of differential element is 10,20 and 30,which means fine level of the optimized fin.The final optimization result is shown in Table 4.

Table 4The performance of conical with different element numbers

As shown in Table 4,the obtained result has obvious difference when the number of differential element is 10 and 20.While the result deviation between 20 and 30 differential elements is less than 0.1%.So in the view of the computational cost,20 element division is chosen in present work.

5.3.2.Error of energy conservation

According to law of the conservation of energy,qbshould be equal toqh.Thus,the relative error betweenqbandqhcould be described as follows,

As shown in Table 5,the relative error betweenqbandqhis less than 3%.So,it can be thought that the optimum results obtained in present work are credible.

Table 5The relative error between q b and q h

6.Conclusions

In the present work,the conical fin has been optimized by an innovative use of the stepping genetic algorithm.To insure the optimization result of conical fin more accurate and reliable,a method similar to building construction is proposed.The optimization of conical fin is performed step by step.

In order to modify the genetic algorithm,the selection of the crossover and mutation probability has been investigated.It's found that a better result of optimization of conic fin could be obtained whenPc=0.7 andPm=0.035 after 60 generations.

Compared with the optimized result of conical fin by Bezier curves,the performance parameters of presentoptimization result are superior to that of reported previous.

Compared with some typical fins such as rectangular fin,triangular fin and pin fin,the present optimization result has remarkable advantage.The stepping genetic algorithm may be an effective method in optimization problems of fins.And the new kind of stepping genetic algorithm could be applied to various kinds of fin optimization problems with one-dimensional temperature distribution and steady state heat conduction.

Nomenclature

Acscross-sectional area,m2

Assurface area,m2

As0the total surface area of fin,m2

ethe relative error

Hfin height,m

hconvective heat transfer coefficient,W⋅m-2⋅K-1

kthermal conductivity,W⋅m-2⋅K-1

mslope of the generatrix of differential element of fin

Npopulation size

NINDmaximum number of generation

Pccrossover probability

qbthe heat conduction rate of the base of the fin,W

qhthe convection heat transfer rate from the fin surface,W

qobobjective function,W

qob-maxmax value of objective function,W

Pmmutation probability

Tbbase temperature of fin,K

Tfambient fluid temperature,K

δbbase cross-section diameter,m

δtterminal cross-section diameter,m

η fin efficiency

Subscripts

b base

c cross over

cs cross section

f fluid

h heat transfer

m mutation

ob objective function

ob-max max value of the objective function

s surface

s0 total surface

t terminal

[1]F.Hajabdollahi,H.H.Rafsanjani,Z.Hajabdollahi,Y.Hamidi,Multi-objective optimization of pin fin to determine the optimal fin geometry using genetic algorithm,Appl.Math.Model.36(1)(2012)244-254.

[2]B.Adrian,M.Almogbel,Constructal T-shaped fins,Int.J.Heat Mass Transf.43(2000)2101-2115.

[3]B.Kundu,P.K.Das,Performance and optimum design analysis of convective fin arrays attached to flat and curved primary surfaces,Int.J.Refrig.32(3)(2009)430-443.

[4]G.Lorenzini,L.A.O.Rocha,Constructal design of T-Y assembly of fins for an optimized heat removal,Int.J.Heat Mass Transf.52(5-6)(2009)1458-1463.

[5]B.Kundu,D.Bhanja,Performance and optimization analysis of a constructal T-shaped fin subject to variable thermal conductivity and convective heat transfer coefficient,Int.J.Heat Mass Transf.53(1-3)(2010)254-267.

[6]X.Zhang,D.Liu,Optimum geometric arrangement of vertical rectangular fin arrays in natural convection,Energy Convers.Manag.51(12)(2010)2449-2456.

[7]B.Kundu,D.Barman,An analytical prediction for performance and optimization of an annular fin assembly of trapezoidal pro file under dehumidifying conditions,Energy36(5)(2011)2572-2588.

[8]B.Kundu,K.S.Lee,Optimum con figurations of vertical fins under condensation of saturated vapor,Int.J.Refrig.34(4)(2011)1048-1056.

[9]Y.Feng,Y.X.Li,Analysis simulation and optimization design of annular fins,Refrigeration38(1)(2009)53-55.

[10]N.Nagarani,K.Mayilsamy,A.Murugesan,Fin effectiveness optimization of elliptical annular fins by genetic algorithm,Procedia Eng.38(2012)2939-2948.

[11]D.Copiello,G.Fabbri,Multi-objective genetic optimization of the heat transfer from longitudinal wavy fins,Int.J.Heat Mass Transf.52(5-6)(2009)1167-1176.

[12]H.Azarkish,S.M.H.Sarvari,A.Behzadmehr,Optimum design of a longitudinal fin array with convection and radiation heat transfer using a genetic algorithm,Int.J.Therm.Sci.49(11)(2010)2222-2229.

[13]H.Azarkish,S.M.H.Sarvari,A.Behzadmehr,Optimum geometry design of a longitudinal fin with volumetric heat generation under the influences of naturalconvection and radiation,Energy Convers.Manag.51(10)(2010)1938-1946.

[14]Y.Wang,Y.L.He,D.H.Mei,W.Q.Tao,Optimization design of slotted fin by numerical simulation coupled with genetic algorithm,Appl.Energy88(12)(2011)4441-4450.

[15]R.Das,Application of genetic algorithm for unknown parameter estimations in cylindrical fin,Appl.Soft Comput.12(11)(2012)3369-3378.

[16]Z.Iqbal,K.S.Syed,M.Ishaq,Optimal fin shape in finned double pipe with fully developed laminar flow,Appl.Therm.Eng.51(1-2)(2013)1202-1223.

[17]M.A.Moon,K.Y.Kim,Analysis and optimization of fan-shaped pin- fin in a rectangular cooling channel,Int.J.Heat Mass Transf.72(2014)148-162.

[18]K.Ryu,S.J.Yook,K.S.Lee,Optimal design of a corrugated louvered fin,Appl.Therm.Eng.68(1-2)(2014)76-79.

[19]J.H.Lienhard IV,J.H.Lienhard V,A heat transfer textbook,third ed.Phlogiston Press,Cambridge,2008 165-166.

[20]A.Yunus,Cengel-heat transfer—A practical approach,second ed.McGraw-Hill,New York,2006 165-166.

[21]S.M.Homayouni,S.H.Tang,O.Motlagh,A genetic algorithm for optimization of integrated scheduling of cranes,vehicles,and storage platforms at automated container terminals,J.Comput.Appl.Math.270(2014)545-556.

[22]O.A.Arqub,Z.A.Hammour,Numericalsolution of systems of second-order boundary value problems using continuous genetic algorithm,Inf.Sci.279(2014)396-415.