琼东南盆地深水区中央峡谷油气指标的多重分形性分析

张焱，张迎朝，杨希冰，周永章，周杰，朱继田

（1.中海石油（中国）有限公司湛江分公司，广东湛江524057；2.中山大学地球科学与地质工程学院，广东广州510275；3.广东省地质过程与矿产资源探查重点实验室，广东广州510275）



琼东南盆地深水区中央峡谷油气指标的多重分形性分析

张焱1，张迎朝1，杨希冰1，周永章2，3，周杰1，朱继田1

（1.中海石油（中国）有限公司湛江分公司，广东湛江524057；2.中山大学地球科学与地质工程学院，广东广州510275；3.广东省地质过程与矿产资源探查重点实验室，广东广州510275）

摘要：不同形态的多重分形频谱可用于含油气远景评价和油气分布规律的研究，本文运用多重分形矩方法对中央峡谷体系已钻井获得的2 684个数据13项油气指标的多重分形谱函数形态特征进行了研究。结果表明，琼东南盆地深水区中具有较强多重分形特征的指标，具有多重分形谱函数宽而连续的特征，成一右偏弧形状；而其他指标则显示较弱或单一分形特征。将这一结果与常用的统计方法因子分析结果做对比，结果表明，通过多重分形分析对这几项油气指标的分组结果与常规的统计分析结果基本吻合。为更进一步探究这几种主要油气指标在油气指示中的权重，采用主成分分析法对这几种指标进行分析，结果表明在琼东南盆地深水区，异丁烷、正丁烷、异戊烷为圈定油气远景区的重要指标。

关键词：琼东南盆地；中央峡谷；多重分形；油气指标

1　引言

分形用于描述不规则事物形态特征已在地学界得到了广泛的应用。而分形维数是反映其结构特征复杂程度一个很重要的参数，根据维数值可以定量的描述事物的复杂程度。单一分形具有唯一的分维数值，且标度是不变的；单个分维不足以描述自然界特征，通常需要多个分形维数来描述，也即多重分形。实际上，多重分形也就是许多个单一分形的相互缠结［1］。近年来，多重分形在固体矿产中应用甚广，如地球化学、地球物理找矿方面，且取得了较显著的成效［2—5］，尤其在描述矿化富集规律时，多重分形模型起到了举足轻重的作用。通过计算机技术等手段模拟的结果表明微量元素的背景值通常服从正态或对数正态分布，而异常值服从分形分布［6］，至今这一结论有效的支撑着地质工作者工作。

尽管越来越多的证据表明元素含量服从分形或多重分形分布，但目前大多数研究仅限于金属元素，而在油气地质领域中较少出现。琼东南盆地深水区中央峡谷领域，随着勘探的逐步深入，对其研究也进一步加深，而纵观多年的研究内容无外乎两方面［7］：一是储层有关峡谷内部充填结构方面，另一方面是沉积研究中有关峡谷形态沉积旋回划分［8—9］；对于油气指示研究方面琼东南盆地深水区中央峡谷还从未涉及。鉴于此，本文运用典型的多重分形方法对琼东南盆地深水区黄流组气样中12项油气指标的多重分形谱函数形态特征进行研究。

2　数据和方法

2.1数据来源与分析

研究区位于琼东南盆地深水区中央峡谷领域，中央峡谷体系位于深水区中央坳陷带，整体呈“S”型N E向展布（图1），西起莺歌海盆地中央凹陷带东缘，经乐东凹陷、陵水凹陷、松涛凹陷、宝岛凹陷、长昌凹陷，向东延伸进入西沙海槽［10—11］。本研究中的数据来源于峡谷体系钻井获得的气测数据，包括甲烷、乙烷、丙烷、正丁烷、异丁烷、正戊烷、异戊烷这几个参数，都是用氢火焰离子探测器色谱仪测量钻井液中各个烃类组分含量的大小得到的。

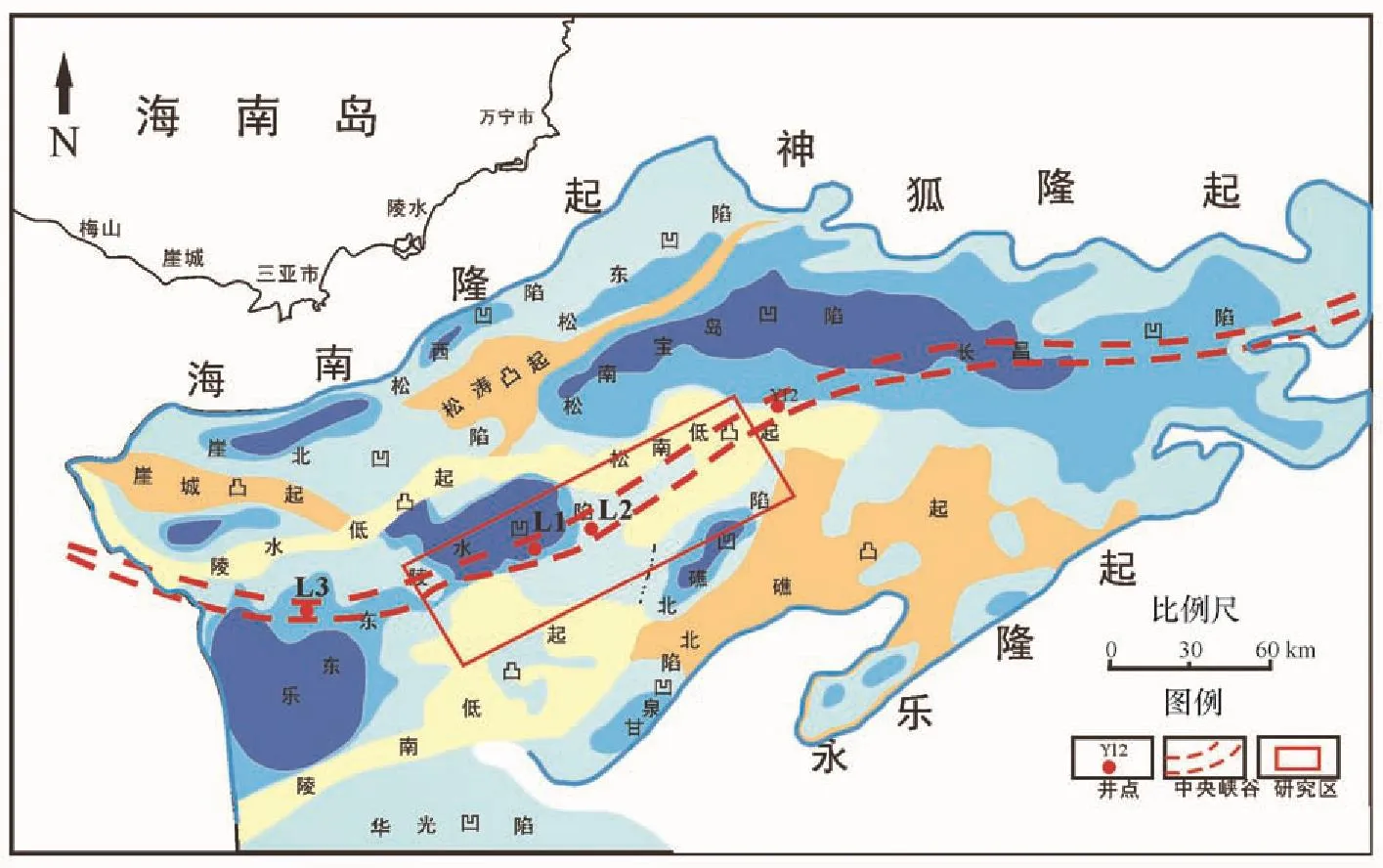
图1　研究区位置图Fig.1 The position of the study area

文中使用的指标及其指示意义见表1，其中A1 = （C1 + C2）/（C3 + C4 + C5）为平衡比，A2 =（C4 + C5）/ C3为特征比，A3 = iC5/nC5为微运移指数，A4 = C2 + C3 + C4 + C5为重烃，A5 = C1/（C2 + C3 + C4 + C5）为轻烃与重烃比，A6为干燥比。

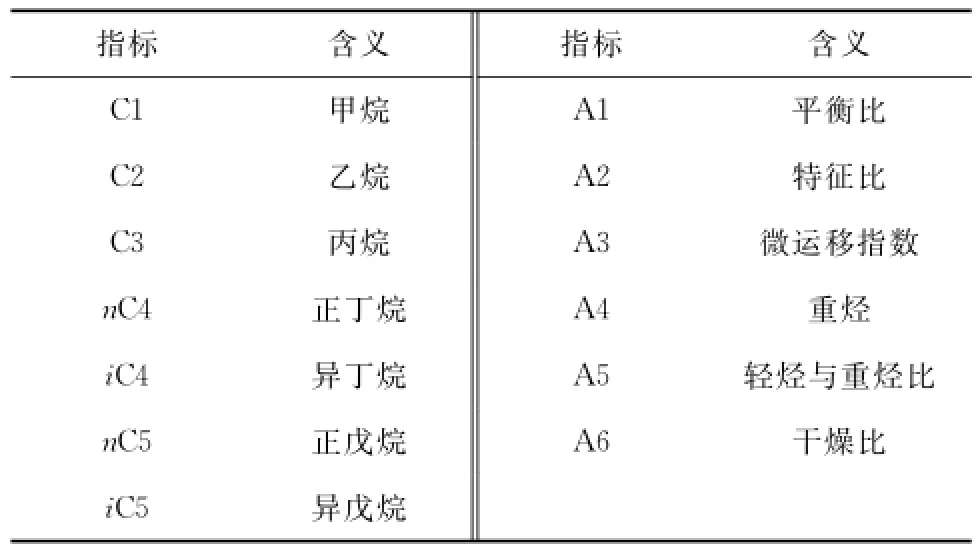
表1　油气指标及其含义Tab.1 Definition of symbols used in the paper

2.2多重分形方法

多重分形是单一分形的推广，推广至空间上通常为单一分形的相互缠结，它所描述的是定义在二维或三维中的一种度量，若这种度量具有空间或统计上的自相似性，则将这种量称之为多重分形。具有多重分形性质的数据的奇异性可以将所定义区域分解成一系列单一分形这样的子区域。这些子区域不仅具有分形维数，还具有各自度量的奇异性，所有这些子区域的分形维数和奇异性组成维数谱函数f（α）。

计算多重分形谱函数最常见的方法为直方图法［12］，类似的还有小波方法、乘数法和矩方法等，而矩方法是最常用的方法之一［13］。

矩方法计算f（α）的步骤为［14］：

（1）首先构建分配函数Xq（ε）=∑n（ε）（xiε2）qi，双对数图上将质量分配函数Xq（ε）与网格大小ε表现出来。其中q为任意数，对应u（ε）的统计矩阶数，xiε2表示第i个长度为ε的单元金属总量，xi为第i个单元的品味值。此处以研究区指标特征比的分析结果为例。文中q值从-10到10（-10，-9，-8，…，0，…，9，10），步长为1，从图2得知分配函数与步长呈较好的线性关系，q值变化，直线的斜率相应的改变，图中的线条表示q值为-10，-9，…，0，…，10对应的线条。

（2）质量指数τ（q）的计算方法根据质量分配函数而定，若u（ε）具有多重性，那么对于任意q值，存在Xq（ε）∝ετ（q）这种指数关系，可根据图2中τ与q之间的斜率来计算质量指数。

（3）奇异指数α（q）的计算公式为：α（q）=∂τ（q）/ ∂q。

（4）计算分形维数f（α）：f（α）=α（q）q-τ（q）。

由图2（图2a为分配函数Xq（ε）与度量尺度ε在双对数坐标图上的关系，图2b为质量指数τ（q）与矩级次q之间的关系图；图2c为奇异指数α（q）与矩级次q之间的关系图；图2d为多重分形谱函数f（α）与奇异指数α（q）的关系图）可有效的判断所研究对象是单一分形还是多重分形；如果矩级次q与质量指数τ（q）为线性关系，则分析对象为单一分形；如果q与τ（q）之间为一曲线关系，则分析对象为多重分形，并且其之间的曲率可以通过［τ（q）-τ（1）］/（q-1）计算得知。另外，如若τ（q）与q为线性关系，则奇异指数α（q）应基本保持定值在q-α图中表现为一条平行q值的直线，而分形维数f（α）与α的关系表现为倒尖钩状。若研究对象为多重分形，奇异指数α（q）与矩级次q应为曲线关系，通常奇异指数α（q）的波动范围相对变大。

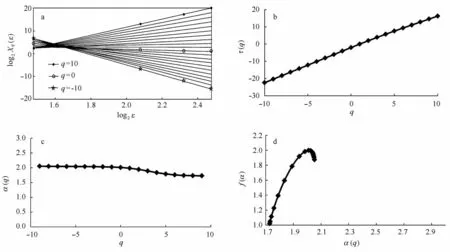
图2　矩方法计算琼东南盆地深水区中央峡谷黄流组特征比［（C4 + C5）/C3］指标多重分形谱函数步骤Fig.2 The steps of the method of moments to analyze the multifractal spectrum of［（C4 + C5）/C3］in central canyon of Qiongdongnan Basin deepwater area

3　分析与讨论

3.1矩方法分析

首先采用矩方法计算各指标的多重分形谱函数，取q值从-10到10，步长为1。图2-图5分别给出了琼东南盆地深水区中央峡谷内几种油气地球化学指标的矩方法分析结果。从图3得知，对于中央峡谷体系的C1，其分配函数与尺度长度之间的双对数函数呈较好的线性关系；质量指数τ（q）与矩级次q之间的曲率较小，近似为一条直线；奇异指数α与矩级次q之间为一曲线，其多重分形谱宽且连续，这说明C1指标在峡谷体系中的空间分布显示连续多重分形特征。

相对于C1来说，C2的f（α）-α曲线中f（α）最小值接近1.2（图4），而C1的f（α）最小值趋于1，曲线形态上有所变化，另外，相对于C1来说C2中奇异指数α与q之间的拖尾似乎比C1的更为明显。

从图2得知，尽管特征比的质量指数τ（q）与q间的曲率较小近似一条直线，而α（q）与矩级次q之间的曲线形态也不明显，由此看来特征比在该工区近似表现为单一分形特征。

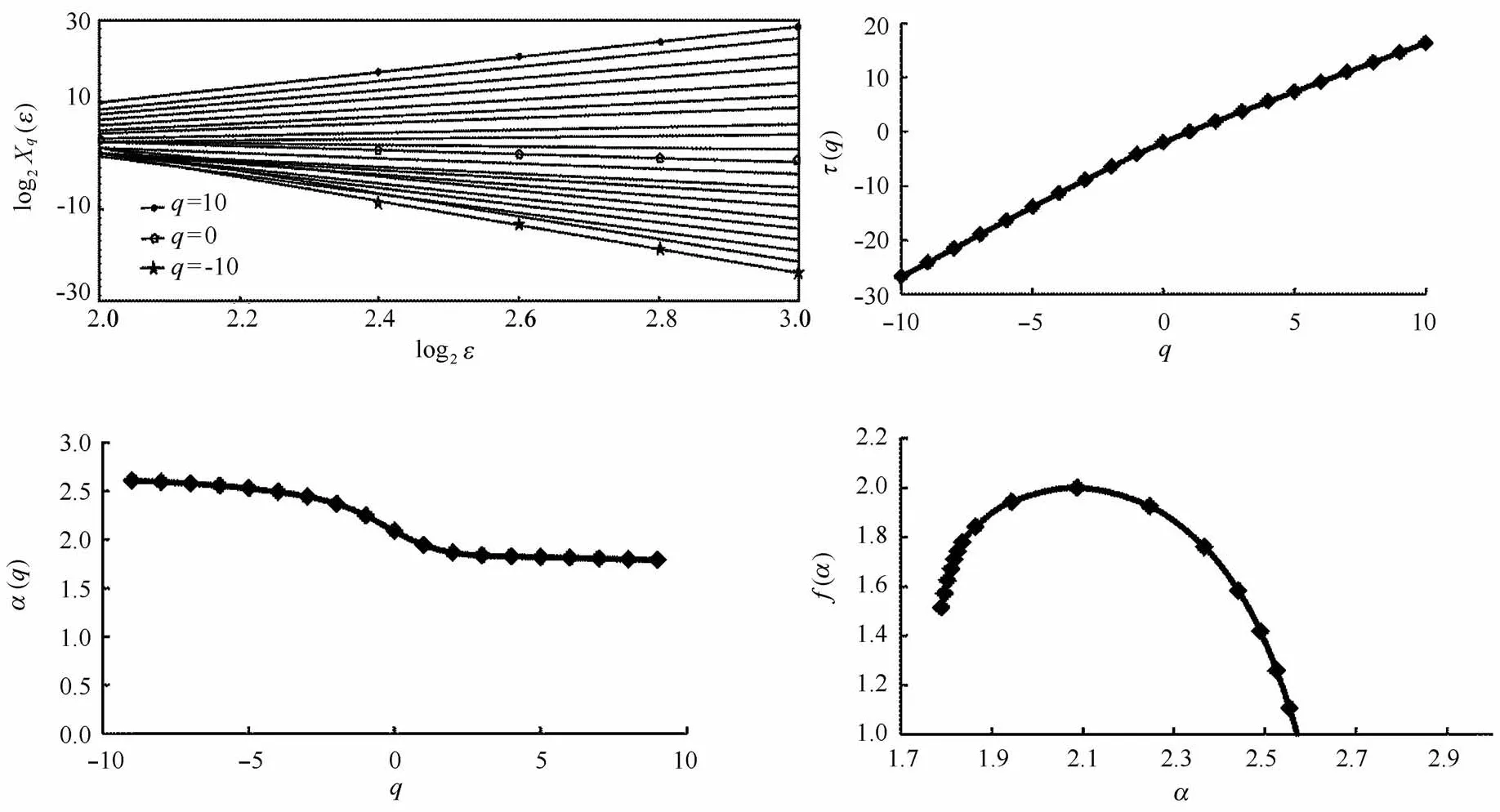
图3　琼东南盆地深水区中央峡谷C1指标的多重分形谱函数形态特征Fig.3 M ultifractal analysis of C1 in central canyon of Qiongdongnan Basin deepwater area

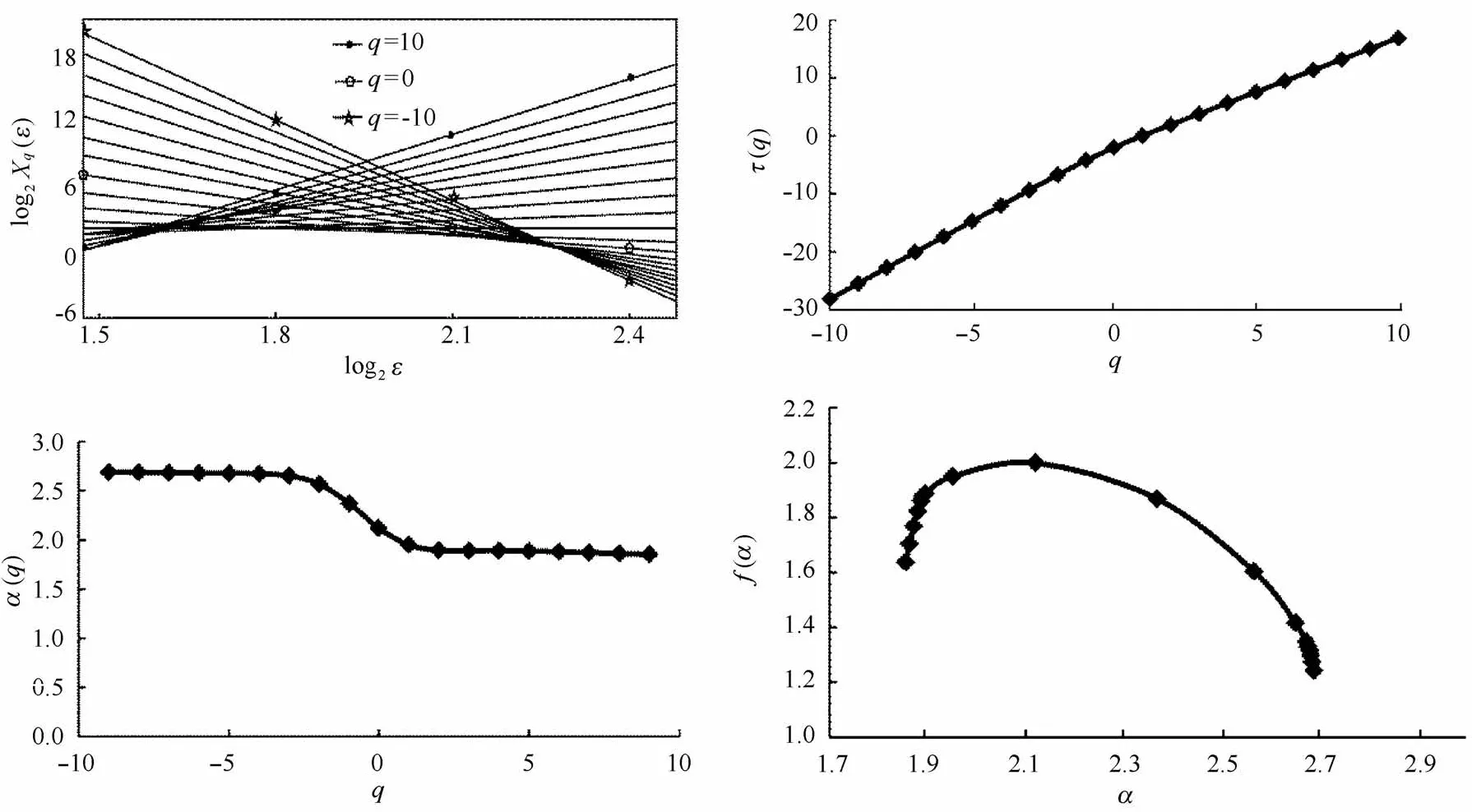
图4　琼东南盆地深水区中央峡谷C2指标的多重分形谱函数形态特征Fig.4 M ultifractal analysis of C2 in central canyon of Qiongdongnan Basin deepwater area

对于干燥系数指标来说，分配函数和尺度在双对数图上表现出较好的线性关系，质量指数τ（q）与矩级次q之间也也具有良好的线性关系，以致奇异指数α 与q表现为一条水平直线，其分形谱函数近似表现为一个定值。

对研究区12项指标研究发现，根据多重分形谱的形态特征（文中给出具有代表性的部分指标图件）及各参数（表2），大致可以将研究区油气指标分为3大类。

（1）C1、C2、C3、nC4、iC4、nC5、iC5和重烃为一类，其多重分形谱函数宽而连续Δα和Δf（α）值均较大，［τ（q）-τ（1）］/（q-1）值的变化较大，显示较强的多重分形特征。

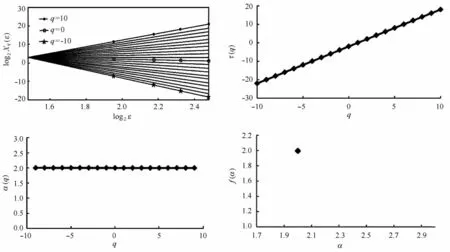
图5　琼东南盆地深水区中央峡谷干燥系数［C1/（C1 + C2 + C3 + C4 + C5）］指标的多重分形谱函数形态特征Fig.5 M ultifractal analysis of［C1/（C1 + C2 + C3 + C4 + C5）］in central canyon of Qiongdongnan Basin deepwater area

（2）轻烃与重烃比、干燥系数和平衡比为第二类，这三项指标的Δα和Δf（α）大约为0.3～0.5之间，［τ（q）-τ（1）］/（q-1）的波动范围在2.1左右，体现了较弱的多重分形特征；而另外更进一步分析发现，干燥系数指标指标还可从这一类中单独分离出来，因为其Δα趋于0，［τ（q）-τ（1）］/（q-1）值更趋于2，体现了微弱的多重分形特征。

（3）微运移和特征比为第三类。这一组Δα和Δf（α）值均较小，［τ（q）-τ（1）］/（q-1）的波动范围也小，显示近似单一分形特征。

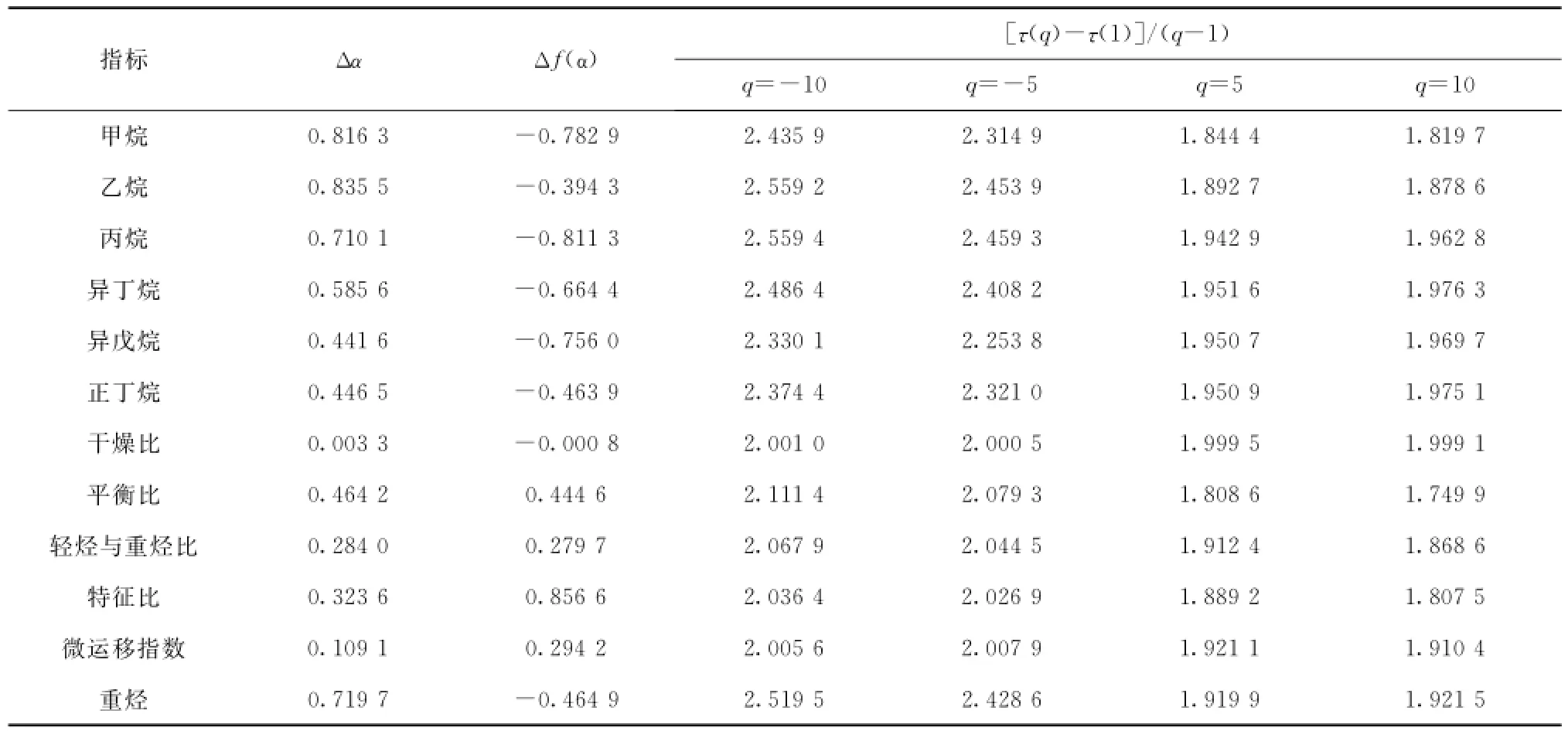
表2　琼东南盆地深水区中央峡谷油气指标多重分形分析参数一览表Tab.2 Some parameters of indices from oil samples in central canyon of Qiongdongnan Basin deepwater area

3.2油气指标相关性分析

湛江分公司在探讨油气指标之间的相关性时，通常是采用因子分析法进行分析，根据琼东南盆地深水区中央峡谷黄流组油气指标因子成分图6得知油气指标在该区的相关关系，因子分析结果将这些指标分为三组，第一组为由多重分形得到的具有较强多重分形特征的8项指标C1、C2、C3、iC4、nC4、iC5、nC5、重烃组合，第二组为轻烃与重烃比、平衡比和干燥系数组合，第三组为特征比和微运移指数组合。从分析结果可以看出，该区通过多重分形分析和常规的统计分析对这几项油气指标的分组结果基本吻合。

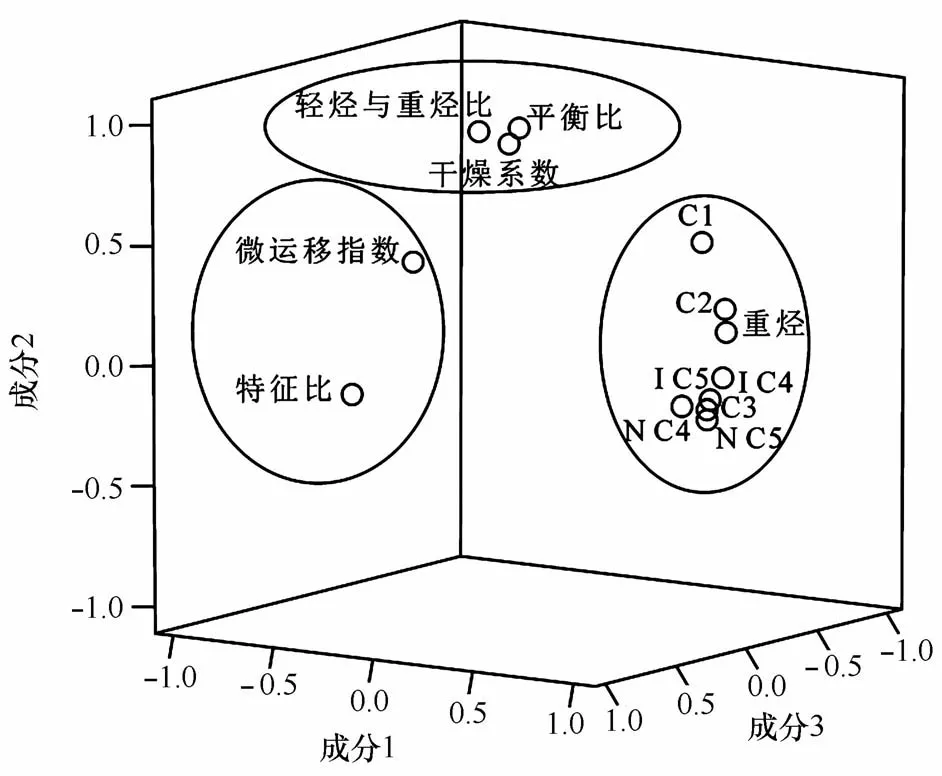
图6　琼东南盆地深水区中央峡谷黄流组油气指标因子成分图Fig.6 Oil and gas index factor composition diagram for H uangliu formation in centralcanyon of Qiongdongnan Basin deepwater area

已有研究表明［14］，C2和C3是圈定油气远景区的主要指标，而C1则为圈定远景区的重要补充；而针对琼东南盆地深水区，从上述分析得知，深水区主要油气指标如C1、C2、C3、iC4、nC4、iC5、nC5等服从较强的多重分形性质，而其他指标则服从弱的多重分形性质甚至是单一分形，这一点与金属场的研究结果也较为吻合［15］，这说明深水区主要油气指标也服从多重分形分布［16］。

为更进一步探究这几种指标在油气指示中的权重，采用主成分分析法同时对这几种指标进行分析［17—19］，鉴于深水区主要油气指标C1、C2、C3、iC4、nC4、iC5、nC5较强的多重分形性，分析前需要对这几种指标进行进行对数变换，第一主成分的载荷图和特征分布见图8。从累积方差图（图7）得知第一主成分特征值最大，约占方差的67 %。第一主成分反映了所有这几种具有多重分形特征的指标，贡献最大的为iC4、nC4、iC5，这说明在琼东南盆地深水区，iC4、nC4、iC5为圈定油气远景区的重要指标。

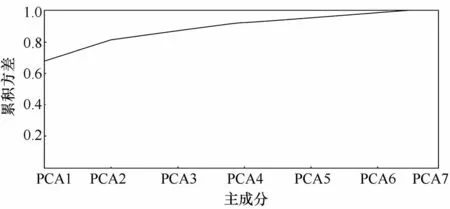
图7　对主要油气指标进行主成分分析后累积方差图Fig.7 Cumulative variance for principal component analysis of the main oil and gas index

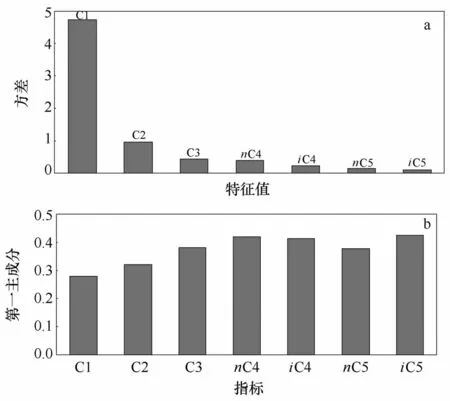
图8　对各指标C1、C2、C3、iC4、nC4、iC5、nC5对数变换值进行主成分分析结果Fig.8 Principal component analysis results of logtransformed values of C1、C2、C3、iC4、nC4、iC5、nC5

4　结论

（1）分形与多重分形性质可能存在于油气指标中，而矩方法可以较好的指示油气指标效果；

（2）琼东南盆地深水区中具有较强多重分形特征的指标具有多重分形谱函数宽而连续的特征，且［τ（q）-τ（1）］/（q-1）值的变化较大；而具有较弱多重分形特征的指标［τ（q）-τ（1）］/（q-1）的波动范围趋于2。可根据多重分形频谱形态来判断油气远景区。

参考文献：

［1］Stanley H E，M eakin P.M ultifractal phenomena in physics and chemistry［J］.Nature，1998，335（6189）：405-409.

［2］Agterberg F P.M ultifractal simulation of geochemical map patterns［J］.Journal of China U niversity of Geosciences，2001，12（1）：6-14.

［3］Cheng Q M.Vertical distribution of elementsin regolith over mineral deposits and implications for mapping geochemical weak anomaliesin covered areas［J］.Geochemistry：Exploration，Environ ment，Analysis，2014，14（3）：162-175.

［4］Cheng Q M.Generalized binomial multiplicative cascade processes and asym metrical multifractal distribution［J］.Nonlinear in Processes Geophysics，2014，21（2）：477-487.

［5］Cheng Q M.M ultifractalInterpolation M ethod for Spatial Data with Singularities［J］.Journal ofthe Shouthern African Insitute of Mining and M etallurgy，2015，115（3）：235-240.

［6］成秋明.多重分形理论与地球化学元素分布规律［J］.地球科学，2000，25（3）：311-318.Cheng Qiu ming.M ultifractal theory and geochemical element distribution pattern［J］.Earth Science，2000，25（3）：311-318.

［7］张道军，王亚辉，赵鹏肖，等.南海北部琼东南盆地陵水段峡谷沉积建造及勘探意义［J］.海洋学报，2015，37（2）：25-35.Zhang Daojun，W ang Yahui，Zhao Pengxiao，et al.Sedimentary formation and exploration significance ofthe Lingshui Canyon system in the Qiongdongnan Basin，northern South China Sea［J］.Haiyang Xuebao，2015，37（2）：25-35.

［8］王振峰.深水重要油气储层—琼东南盆地中央峡谷体系［J］.沉积学报，2012，30（4）：646-652.W ang Zhenfeng.Important deepwater hydrocarbon reservoirs：the centralcanyon system in the Qiongdongnan Basin［J］.Acta Sedimentologica Sinica，2012，30（4）：646-652.

［9］苏明，解习农，王振峰，等.南海北部琼东南盆地中央峡谷体系沉积演化［J］.石油学报，2013，5（3）：467-478.Su Ming，Xie Xinong，W ang Zhenfeng，et al.Sedimentary evolution of the central canyon system in Qiongdongnan Basin，northern South China Sea［J］.Acta Petrolei Sinica，2013，5（3）：467-478.

［10］苏明，李俊良，姜涛，等.琼东南盆地中央峡谷的形态及成因［J］.海洋地质与第四纪地质，2009，29（4）：85-93.Su Ming，LiJunliang，Jiang Tao，et al.M orphologicalfeatures and formation mechanism of central canyon in the Qingdongnan Basin，Northern South China Sea［J］.M arine Geology & Quaternary Geology，2009，29（4）：85-93.

［11］林畅松，刘景彦，蔡世祥，等.莺-琼盆地大型下切谷和海底重力流体系的沉积构成和发育背景［J］.科学通报，2001，46（1）：69-72.Lin Changsong，Liu Jingyan，Cai Shixiang，et al.Depositionalarchitecture and developing settings oflarge-scaleincised valley and sub marine gravity flow systems in the Yinggehai and Qiongdongnan Basins，South China Sea［J］.Chinese Science Bulletin，2001，46（1）：69-72.

［12］Evertsz C J G，M andelbrot B B.M ultifratal measures（Appendix B）［M］//Chaos and Fractals.New York：Springer Verlag，1992：922-953.

［13］Halsey T C，Jensen M H，Kadanoff L P，et al.Fractal measures and their singularities，the characterization of strange sets［J］.Phys Rev，1986，33（2）：1141-1151.

［14］谢淑云，鲍征宇，苏江玉，等.新疆塔里木盆地艾协克-桑塔木南地区油气地球化学指标的多重分形性分析［J］.地质论评，2005，51（1）：107-112.Xie Shuyun，Bao Zhengyu，Su Jiangyu，et al.M ultifractal properties of oiland gasindexesin the southern Aixieke-Sangtamu region of Xinjiang，China［J］.Geological Review，2005，51（1）：107-112.

［15］Xie Shuyun，Bao Zhengyu.Fractal and multifractal properties of geochemicalfields［J］.M athematical Geology，2004，36（7）：847-864.

［16］张焱，裴健翔，周永章，等.非线性技术在陵水17-2物源分析和储层预测中的应用［J］.地质学报，2016，90（3）：559-568.Zhang Yan，Pei Jianxiang，Zhou Yongzhang，et al.The Application of Nonlinear Techniques on Provenance Analysis and Reservoir Parameter prediction at Lingshui 17-2［J］.Acta Geologica Sinica，2016，90（3）：559-568.

［17］张焱，周永章.奇异性理论在钦杭成矿带（南段）庞西垌银金矿产资源预测中的应用［J］.中南大学学报（自然科学版），2012，43（9）：3558-3564.Zhang Yan，Zhou Yongzhang.Application of singularity theoryin prediction of silver and gold mineral depositsin Qinzhou-Hangzhou tectonicjoint belt Pangxidong Area，Guangdong，China［J］.Journal of Central South U niversity，2012，43（9）：3558-3564.

［18］Yang J，Cheng Q M.A comparative study ofindependent component analysis with principalcomponent analysisin geological objectsidentification.PartⅡ：A case study of Pinghe District，Fujian，China［J］.Journal of Geochemical Exploration，2015，149：136-146.

［19］陈浙春，程同锦，汤玉平，等.油气化探在塔里木盆地油气勘探中的应用［J］.天然气地球科学，2005，16（1）：59-63.Chen Zhechun，Cheng Tongjin，Tang Yuping，et al.Application results of oiland gas geochemicaltechniquein oiland gas exploration in tarim basin［J］.Natural Gas Geoscience，2005，16（1）：59-63.

张焱，张迎朝，杨希冰，等.琼东南盆地深水区中央峡谷油气指标的多重分形性分析［J］.海洋学报，2016，38（5）：133-140，doi：10.3969/j.issn.0253-4193.2016.05.012

Zhang Yan，Zhang Yingzhao，Yang Xibing，et al.M ultifractal properties of oil and gasindexesin central canyon of Qiongdongnan Basin deepwater area［J］.Haiyang Xuebao，2016，38（5）：133-140，doi：10.3969/j.issn.0253-4193.2016.05.012

M ultifractal properties of oil and gasindexesin central canyon of Qiongdongnan Basin deepwater area

Zhang Yan1，Zhang Yingzhao1，Yang Xibing1，Zhou Yongzhang2，3，Zhou Jie2，Zhu Jitian1
（1.China National Offshore Oil Corporation Limited，Zhanjiang 524057，China；2.Schoolof Earth Science and Geological Engineering，Sun Yat-sen University，Guangzhou 510275，China；3.Guangdong Provincial Key Laboratory of Geological Processes and Mineral Resource Survey，Guangzhou 510275，China）

Abstract：Different M ultifractalspectru m can be used for petroleu m prospect evaluation.A typical multifractal model called the method of moments is employed to study the distribution patterns based on the multifractal spectru m forms obtained from 13 oil and gas indexes and 2 684 data in the deepwater area of central canyon of the Qiongdongnan basin.The results show that the indicators with strong multi-fractal characteristics in deepwater have wide and continuous fractal spectru m function features，forming a right side arc shape.W hile otherindicators display weak or single fractalfeature.Comparing the result with the one from factor analysis，shows that these results are generally consistent.In order to further examine the weights of these oil and gasindexes，principal component analysis was used to analyze these indicators.The resultsindicate thatisobutane，normal butane，iso-pentane is importantindicators to delineate hydrocarbon in the deepwater area.

Key words：Qiongdongnan Basin；central canyon；multifractal；oil and gas indexes

作者简介：张焱（1983—），女，湖北省孝感市人，博士，主要从事石油地质、数学地质综合研究。E-mail：zhang_yan1117＠163.com

基金项目：“十二五”国家重大科技专项（2011ZX05025）。

收稿日期：2015-10-29；

修订日期：2016-03-14。

中图分类号：P618.13

文献标志码：A

文章编号：0253-4193（2016）05-0133-08