基于修订Copula函数的中国干旱特征研究

陈再清，侯　威，左冬冬,3，胡经国

(1.扬州大学物理科学与技术学院，江苏　扬州　225002；2.国家气候中心气候研究开放实验室，北京　100081；3.扬州大学数学科学学院，江苏　扬州　225002)



基于修订Copula函数的中国干旱特征研究

陈再清1,2，侯威2，左冬冬2,3，胡经国1,2

(1.扬州大学物理科学与技术学院，江苏扬州225002；2.国家气候中心气候研究开放实验室，北京100081；3.扬州大学数学科学学院，江苏扬州225002)

摘要：利用中国613个站点1961～2010年逐月降水数据，基于游程理论从月标准化降水指数(SPI)序列中分离出干旱事件，并通过K-S检验方法对其干旱强度和干旱历时2个特征量的分布函数进行检验。在此基础上，利用Copula函数建立2个特征量的二维联合概率分布函数，对比分析干旱历时分布函数修订前后对不同类型干旱联合概率及重现期的影响。结果表明：干旱强度特征量符合Gamma分布，而干旱历时特征量并非完全符合指数分布，因此需对干旱历时分布函数进行必要的修订。在干旱历时分布函数修订情况下，大部分干旱类型的联合概率减小，少部分干旱类型的联合概率增大；且不同类型干旱的联合重现期增大。在干旱历时尺度相同时，随着干旱强度的增加，最大和最小联合重现期的差异无明显变化；但在干旱强度相同时，最大和最小联合重现期的差异随着干旱历时的增加而明显增大。

关键词：干旱；游程理论；Copula函数；修订

引言

干旱是指在长期无降水或降水异常偏少的气候背景下，由于水分收支或供求不平衡而形成的水分短缺现象[1]。按照传统划分方法，干旱可分为气象干旱、水文干旱、农业干旱和社会经济干旱[2]，本文主要研究气象干旱。干旱是我国影响面积最广的气象灾害，其对我国农业生产的影响尤为严重，据统计：2014年全国作物受旱面积2.3×108hm2、受灾面积1.2×108hm2、成灾面积567.7万hm2、绝收面积148.5万hm2，因旱造成粮食损失2 006万t、经济作物损失276亿元、直接经济总损失910亿元[3]。

由于大气运动的非线性和复杂性，干旱问题的研究也相对复杂[4-8]。干旱的特征可以用干旱强度和干旱历时等变量来描述，然而单变量的分析难以反映多变量内部的相关性，同时传统的多变量频率分析法受变量边缘分布函数类型的限制，无法有效地对干旱的统计特征进行描述[9]。Sklar提出的Copula函数能够很好地解决这一问题[10]，各变量的边缘分布函数可以采用任一形式，适合用来构建边缘分布函数为任意分布的联合分布函数，因而该方法得到广泛应用[11-16]。Copula函数大体上可分为椭圆型、Archimedean型以及二次型3种类型[17]，采用不同形式的Copula模型可能导致不同的分析结果。其中，Archimedean Copula函数以其构造简单、易求解等特点被广泛应用于各个领域。目前Copula函数在水文领域中的应用主要是降雨和洪水的频率分析，而干旱分析的研究尚且不足。另外，Copula函数应用于干旱事件分析中，一般仅计算概率分布和重现期，而对干旱特征的空间分析研究较少[18-20]。

游程理论也叫轮次理论，是分析时间序列的一种方法，被广泛应用于干旱事件的识别中[21-25]。Kolmogorov-Smirnov(K-S)检验是用以检验一经验分布是否符合某种理想分布或比较2个经验分布是否有显著性差异。本文利用中国613个站点1961～2010年月降水数据，基于游程理论、Kolmogorov-Smirnov(K-S)检验，利用Copula函数构建干旱强度和干旱历时2个特征量的联合分布函数，对比分析干旱历时分布函数修订前后对我国不同类型干旱联合概率及重现期的影响。

1资料与方法

1.1资料

采用中国气象局国家气象信息中心提供的1961～2010年全国753站月降水资料。在研究时间段内，只要该站数据存在缺测就剔除该站点，去除缺测站点后共计613站(图略)。

1.2方法

1.2.1SPI指数

降水分布是一种偏态分布，可用Γ分布来描述。McKee等[26]将降水的偏态分布进行标准正态化处理得到标准化降水指数(SPI)，该指数具有结构简单、空间一致和多时间尺度的特征[27]，可用于不同时间尺度的干旱监测和评价。Liu等[11]在此基础上对SPI的计算方法进行了优化。本文SPI指数的计算采用Liu等[11]所述的方法，即月尺度的SPI指数。表1给出SPI指数的干旱等级划分标准。

表1　SPI指数的干旱强度等级分类

1.2.2游程理论

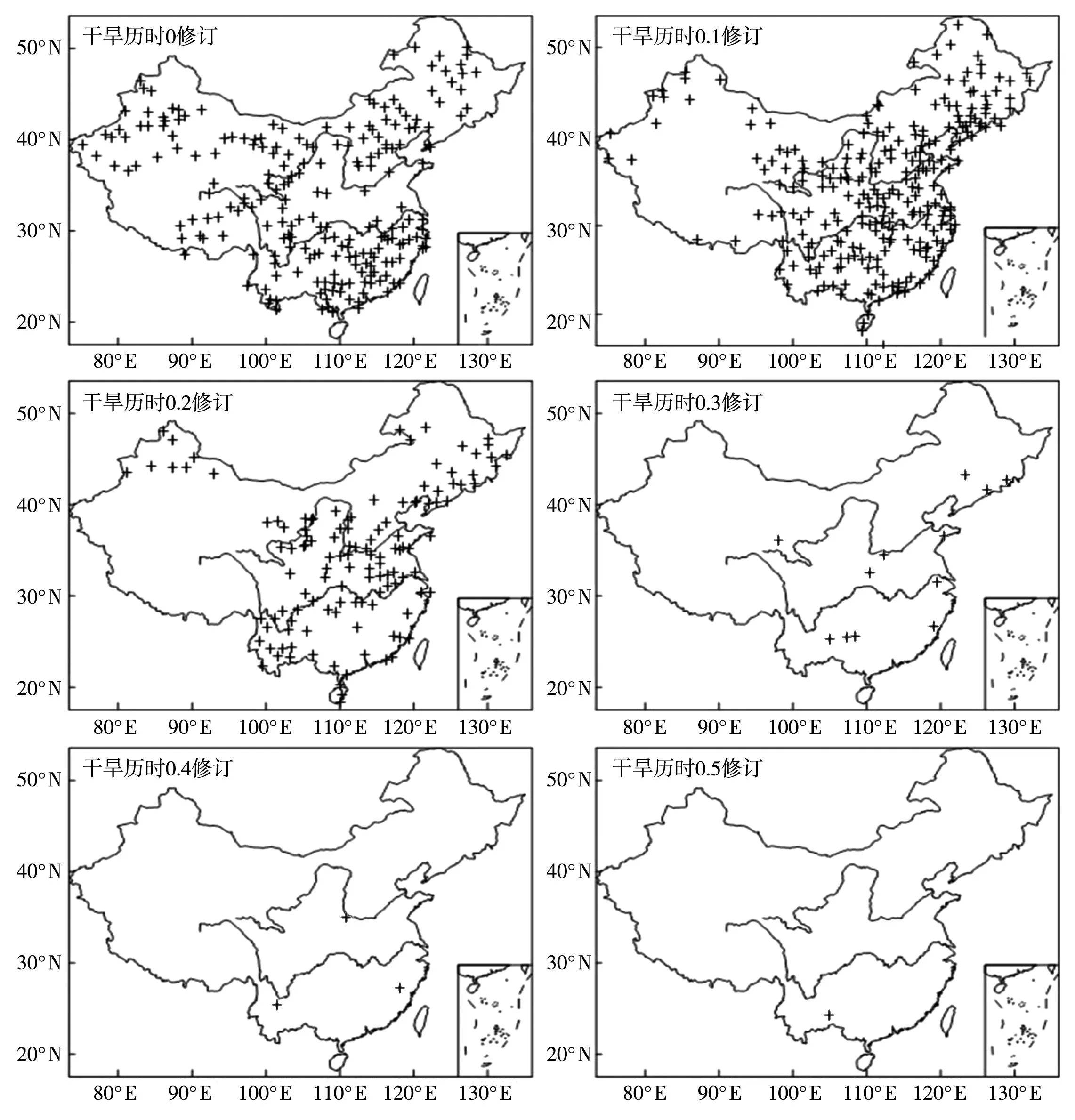
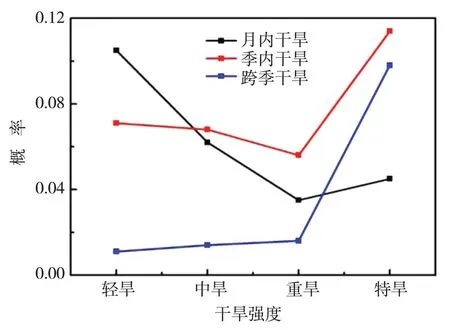
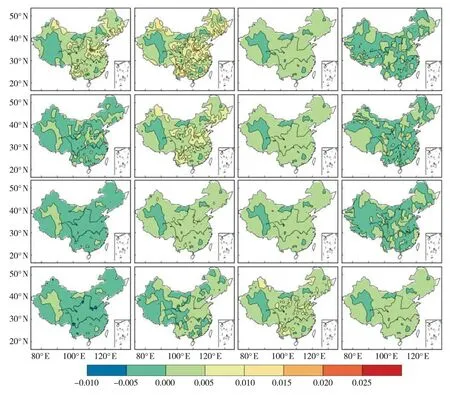
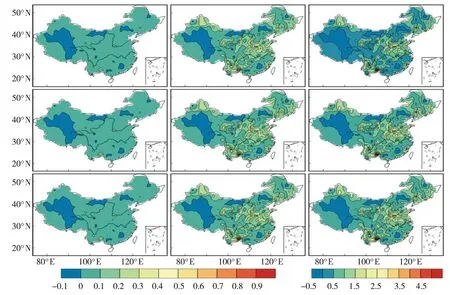
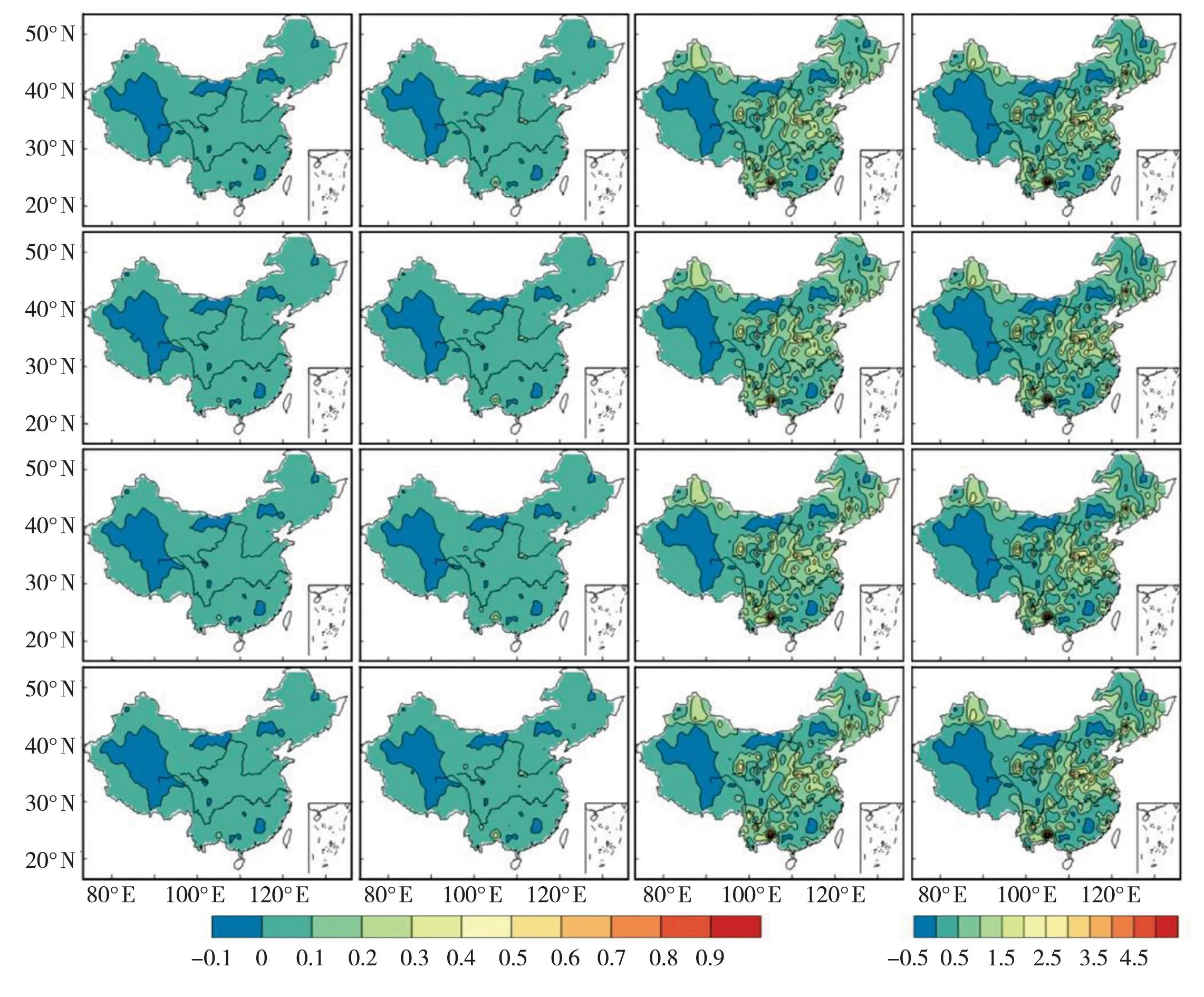
Herbst[28]、Shen[29]、Mohan[30]等先后将游程理论应用于干旱识别研究中。利用游程理论对干旱事件的识别过程(图1)：将月SPI资料视为离散序列，选择SPI为0作为截取水平s0，当月SPI序列在时间段内连续

(1)

图1　游程理论示意图

1.2.3边缘分布函数

基于游程理论方法得到各站点1961～2010年历次干旱事件强度和历时的样本。干旱强度和干旱历时的分布分别符合Gamma分布和指数分布[31-32]。其公式如下：

(2)

(3)

式中，S、s分别为干旱强度的样本空间及其中的元素，D、d分别为干旱历时的样本空间及其中的元素，FS(s)、FD(d)分别表示干旱强度≤s的概率和干旱历时≤d的概率，λ、α、β为分布函数的参数。

1.2.4K-S检验

Kolmogorov-Smirnov(K-S)检验是基于累积分布函数，用以检验一经验分布是否符合某种理想分布或比较2个经验分布是否有显著性差异。K-S检验的实质是计算实际累积频率分布函数和理论累积频率分布函数的差值，若最大值大于临界值，认为理论和实际有显著差异；反之，认为理论和实际无显著差异。当给定临界值时，两者的差值越小则越能通过K-S检验[33]。

令F0(X)表示假设的理论累积分布函数；Fn(X)表示随机样本的累积概率分布函数。2个分布间的差距可表示为：

(4)

当D>D(n,α)时，则随机样本的总体分布不符合理论累积分布，反之则符合理论累积分布。其中D(n,α)是显著性水平为α且样本容量为n时的拒绝临界值(查表可得)。

1.2.5Copula函数

根据公式(2)和(3)得到干旱强度(S)和干旱历时(D)的边缘分布函数FS(s)和FD(d)。利用Copula函数[34-35]对二者进行联合，则联合分布函数F(d,s)为:

(5)

由于Copula函数类型较多，故而Copula函数如何选取将影响联合分布的结果。二维变量分布常用的Archimedean Copula函数有Gumbel-Hougaard型、Frank型和Cook-Johnson型。本文利用样本经验概率和Copula函数联合概率的离差平方和最小作为最优Copula函数选择准则。离差平方和最小准则表达式为：

(6)

式中，Pei是经验频率，Pi是理论频率 ，n为样本数，OLS值越小说明该Copula 函数与其经验点距的误差越小，其拟合度越好。表2为利用离差平方和最小得到的各站点Copula函数偏向类型的统计结果。可以看出，各站的 Copula函数类型一致为Gumbel-Hougaard类型，故而本文使用的Copula函数均为Gumbel-Hougaard类型。

表2　最优Copula函数筛选表

1.2.6重现期

采用Shiau等[32]推导的干旱重现期公式计算干旱重现期，其公式如下:

(7)

(8)

式中，E(L)表示干旱间隔的平均值，为干旱历时和非干旱历时的期望值之和；TS为干旱强度的重现期；TD为干旱历时的重现期，以上变量单位均为a。联合重现期可分为或(D>d∪S>s)、且(D>d∩S>s)2种情形，具体计算如下：

(9)

(10)

利用上述方法可得到中国613站干旱强度和干旱历时2个特征量的联合概率和联合重现期。本文仅求解联合重现期为“且”情形下的结果。“且”指的是干旱强度和干旱历时必须同时大于给定值才认为相同强度和历时的干旱事件重现一次[25]。另外，对干旱历时分布函数修订前后2种情况下的联合概率和联合重现期进行对比分析，以期基于Copula函数的研究方法有所改善。

2结果与分析

2.1中国干旱事件的联合概率空间分布

选择S0=0作为识别干旱事件的标准。首先，根据游程理论分离出全国613个站点1961～2010年干旱事件的干旱强度和干旱历时2个特征量的样本，由特征量样本计算公式(2)与(3)中的参数。然后，利用K-S检验对2个特征量是否符合相应的函数分布进行检验。结果表明，干旱历时特征量并非完全符合指数分布，全国613个站点中仅有36%的站点通过了检验；而干旱强度特征量符合Gamma分布，99%的站点通过了检验。因此，将干旱历时的经验概率分布曲线与理论概率分布曲线对比后，在指数分布函数形式和各参数不变的情况下，对其分布函数进行修订，使得修订后的分布函数与其经验分布函数更为一致。具体修订方法如下：

(11)

根据式(11)，各站点按照不同的修订函数加以修订并进行K-S检验，其中0修订站点219个，0.1修订站点254个，0.2修订站点124个，0.3修订站点12个，0.4修订站点3个，0.5修订站点1个。不同修订的站点分布如图2所示。

图2　干旱历时各修订站点分布图

将干旱历时划分为4个等级(表3)。将表3中4个等级的干旱历时与表1中4个等级的干旱强度进行两两组合，得到不同类型的干旱事件，给出干旱历时分布函数修订下不同类型干旱事件的联合概率空间分布(图3)及其均值变化趋势(图4)和未修订情况下不同类型干旱事件的联合概率空间分布(图略)。

表3　干旱历时等级划分

在干旱历时分布函数修订情况下(图3)，月内轻旱联合概率的分布较为均匀，而季内特旱和跨季特旱的联合概率在黄河以北较大；干旱历时在半年以上的干旱事件的联合概率都比较小。各类型干旱事件联合概率的差异比较明显，跨季特旱、季内特旱和月内轻旱3个类型干旱事件的联合概率明显大于其他类型干旱。其中，跨季特旱的联合概率最小，均值为0.098，季内特旱的联合概率最大，均值为0.114，而月内轻旱的联合概率介于二者之间，均值为0.105，联合概率高值区主要位于西南地区与华中地区。结合图3和图4可知，就月内尺度的干旱事件而言，随着干旱强度的增加，干旱事件的联合概率呈减小趋势，均值依次为0.105、0.062、0.035、0.045，说明干旱历时较短的月内干旱多为轻旱；从季内及跨季时间尺度的干旱事件中看出，随着干旱强度的增加，季内尺度干旱和跨季尺度干旱的联合概率呈增大趋势，联合概率均值分别为0.071、0.068、0.056、0.114和0.011、0.014、0.016，0.098，说明1～3个月的季内干旱和3～6个月的跨季干旱，由于持续时间较长，多发生特旱。

另外，图3中半年以上轻旱事件中的白色部分是因该区域无站点，将站点数据插值成格点数据后，该区域内的格点出现色标以外的值。经查验，白色部分的值比0略小，为负值，由于概率是>0的值，显然该部分插值结果不合理，故而对其直接留白处理。

为更直观地展示修订前后的差异，给出干旱历时分布函数修订前后各类型干旱事件联合概率的差值(图5)。从图5中发现，大部分类型干旱事件在干旱历时分布函数未修订的联合概率略大于修订后的联合概率，然而对于月内和半年以上时间尺度的干旱事件，部分类型干旱有着相反的结果。其中，对于月内轻旱，在干旱历时分布函数未修订时，其在全国大部分地区的联合概率略大于修订后的联合概率；对于季内和跨季时间尺度的干旱事件，这一结果也同样存在。但月内中旱及以上和半年以上重旱及以下的干旱事件，在全国大部分地区的联合概率却略小于修订后的联合概率。就轻旱事件而言，干旱历时分布函数修订后的月内轻旱、季内轻旱、跨季轻旱的联合概率相对于修订前的最大变化率分别为23.7%、31.6%、33.3%，主要分布在西南和华中地区，且随着时间尺度的增大，变化率呈增大趋势，其他强度的干旱事件也存在这一规律。

图3　干旱历时分布函数修订情况下各类型干旱联合概率空间分布

图4　3类干旱联合概率均值变化趋势

在干旱识别中，以实际经验分布作为参照，寻找与经验分布偏差最小的理论分布函数。从公式(11)可看出，理论分布函数处于经验分布函数的右侧，即未修订的干旱历时分布函数对较短的干旱历时概率估计偏小，而对较长的干旱历时概率估计偏大。图5中变化较大的区域即是干旱历时分布函数修订较大的区域。其中，4种月内干旱事件的概率差值主要为负值，即未修订的干旱历时分布函数低估了月内尺度下干旱事件的概率，而季内和跨季的概率差值主要为正值，即未修订的干旱历时分布函数高估了季内和跨季干旱事件的概率。由于干旱历时和干旱强度存在较强的正相关性，尤其是历时越长、强度越大的干旱事件，二者相关性越强。而Gumbel-Hougaard函数存在后尾相关性[20]，对尾部变化十分敏感，能快速捕捉到尾相关的变化。因此干旱历时分布函数修订与否对历时越长、强度越大的干旱事件影响越大，这也能从23.7%、31.6%、33.3%变率中看出。综上所述，干旱历时分布函数修订与否对各类型干旱事件的联合概率影响较大，这也说明了对干旱历时分布函数进行修订的必要性。

图5　干旱历时分布函数修订前后各类型干旱事件的联合概率差值

2.2中国干旱事件的重现期空间分布

根据公式(7)～(10)计算出各种组合类型干旱事件2个特征量(干旱强度和干旱历时)的重现期。在给定的组合区间内，2特征量最小时对应重现期值小，最大时对应重现期值大。图6和图7分别给出“且”情况下，干旱历时分布函数修订后的联合重现期最大值和最小值的空间分布。

由图6和图7可以看出，最大和最小重现期值均随着干旱强度增大而增大。月内不同强度干旱事件的最大和最小重现期均较小且空间上无明显差异，最大重现期略大于最小重现期，如月内轻旱最大重现期为0.6～1.5 a，最小重现期为0.38～0.76 a；季内不同强度干旱事件最大重现期在西南和华中地区较大，而最小重现期的空间分布无明显差异；跨季不同强度干旱事件的最大和最小重现期都表现出西南和华中地区偏大的特征；干旱历时在半年以上的不同强度干旱事件的最小重现期也同样在西南和华中地区偏大。

图8和图9分别给出干旱历时分布函数修订前后最大和最小重现期的差值。可看出，干旱历时分布函数修订与否对重现期也产生一定影响。从公式(10)中发现，重现期的变化主要是由于干旱历时概率以及联合概率的变化引起。以月内轻旱为例，干旱历时分布函数修订后的概率变大(图8)，联合概率变小(图5)，根据公式(10)可得，干旱历时分布函数修订后的重现期大于修订前的。当干旱历时尺度相同时，重现期差异主要受联合概率变化影响。结合图8和图9可看出，随着干旱强度的增加，最大和最小重现期都无明显差异趋势，这与图5的联合概率差值变化一致。另外还发现，对于不同组合类型干旱事件的最大和最小重现期，干旱历时分布函数的修订与否对我国西南以及华中地区影响较大，这再次说明了对干旱历时分布函数修订的必要性。

图6　干旱历时分布函数修订情况下“且”组合类型最大重现期空间分布(单位：a)

图7　干旱历时分布函数修订情况下“且”的组合类型最小重现期的空间分布(单位：a)(干旱类型组合同图3)

图8　干旱历时分布函数修订前后“且”的组合类型下最大重现期差值(单位：a)(干旱类型组合同图6)

图9　干旱历时分布函数修订前后“且”的组合类型下最小重现期值差值(单位：a)(干旱类型组合同图3)

3结论

(1)通过K-S检验发现，全国613站的干旱强度分布函数符合Gamma分布，干旱历时分布函数并非完全符合指数分数。因此，需对干旱历时分布函数进行必要的修订，从而使修订后的干旱历时分布和经验分布更为一致。

(2)干旱历时分布函数修订情况下，全国月内轻旱的联合概率空间分布较为均匀，季内特旱和跨季特旱的联合概率在黄河以北较大，而干旱历时在半年以上的干旱事件的联合概率均较小。各类型干旱事件联合概率的差异较大，其中跨季特旱、季内特旱、月内轻旱3种类型干旱事件的联合概率明显大于其他组合类型。

(3)干旱历时分布函数修订与否，对不同类型干旱事件的联合概率有一定影响。当干旱历时分布函数未修订时，大部分类型干旱事件的联合概率略大于修订后的联合概率；而对月内和半年以上时间尺度的干旱事件，却存在着相反的结果。

(4)干旱历时分布函数修订后，月内不同强度干旱事件的最大和最小联合重现期均较小且空间分布无明显差异，最大重现期略大于最小重现期。随着干旱强度的增大，最大和最小重现期均增大。季内不同强度干旱事件，其最大重现期在西南和华中地区较大，而最小重现期的空间分布无明显差异；跨季不同强度干旱事件，其最大和最小重现期都表现出西南和华中地区较大的特征；干旱历时在半年以上不同强度干旱事件的最小重现期也同样在西南和华中地区较大。

(5)干旱历时分布函数修订与否对不同类型干旱事件的重现期也有一定影响。修订后的干旱历时分布函数计算得到的重现期大于未修订时的重现期。当干旱历时尺度相同时，随着干旱强度的增加，其最大和最小重现期无明显差异；当干旱强度相同时，最大和最小重现期差异均随着干旱历时的增加明显增大。对于不同类型干旱事件的最大和最小重现期，干旱历时分布函数的修订与否对我国西南以及华中地区影响较大。

参考文献：

[1] 王劲松,郭江勇,周跃武,等. 干旱指标研究的进展与展望[J]. 干旱区地理,2007,30(1):60-65.

[2] Glantz D A W M H. Understanding:the Drought Phenomenon:The Role of Definitions[J]. Water International,1985,10(3):111-120.

[3] 中国新闻网. 2014年以来全国因旱灾造成直接经济总损失910亿元[OL]. http://www.chinanews.com/gn/2014/12-25/ 6912507.shtml.2014,12-25.

[4] 封国林,戴新刚,王爱慧,等. 混沌系统中可预报性的研究[J]. 物理学报,2001,50(4):606-611.

[5] Huang J P, Guan X, Ji F. Enhanced cold-season warming in semi-arid regions[J]. Atmospheric Chemistry and Physics, 2012,12:5391-5398.

[6] Huang J P, Minnis P, Wang S W, et al. Dust aerosol effect on semi-arid climate over Northwest China detected from A-Train satellite measurements[J]. Atmospheric Chemistry and Physics,2010,10:6863-6872.

[7] 戴新刚,汪萍,张凯静. 近60年新疆降水趋势与波动机制分析[J]. 物理学报,2013,62(12):527-537.

[8] 戴新刚,张凯静. 20世纪后30年中国西北西部降水年代际变化机理分析[J]. 物理学报,2012,61(19):526-534.

[9] 闫宝伟,郭生练,肖义,等. 基于两变量联合分布的干旱特征分析[J]. 干旱区研究,2007,24(4):537-542.

[10] Sklar M. Fonctions de RépartitionN Dimensions Et Leurs Marges[J]. Publ Inst Statist Univ Paris, 1960,8:229-231.

[11] Liu C L, Qiang Z, Vijay P S, et al. Copula-based evaluations of drought variations in Guangdong, South China[J]. Nat Hazards, 2011,59:1533-1546.

[12] Shiau J T, Reza M, Saralees N. Assessing Multi-site Drought Connections in Iran Using Empirical Copula[J]. Environmental Modeling & Assessment, 2012,17:469-482.

[13] Ummul F A R, Panlop Z. Copula based analysis of rainfall severity and duration: a case study[J]. Theoretical & Applied Climatologyl, 2014,115:153-166.

[14] Kao S C, Rao S G. A copula-based joint deficit index for droughts[J]. Journal of Hydrology, 2010,380:121-134.

[15] 李计,李毅,宋松柏,等. 基于Copulas函数的二维干旱变量联合分布[J]. 水文,2012,32(1):43-49.

[16] 郭生练,闫宝伟,肖义,等. Copula函数在多变量水文分析计算中的应用及研究进展[J]. 水文,2008,28(3):1-7.

[17] 倪增华,刘合香,罗彦丽,等. Copula函数在广西洪涝灾害的降水概率预测中的应用[J]. 气象研究与应用,2014,35(2):32-39.

[18] 李计. 基于Archimedean Copulas函数的多变量干旱频率及空间分析[D]. 杨凌:西北农林科技大学, 2012.

[19] Shiau J T, Song F, Nadarajah S. Assessment of hydrological drought for the yellow river China using copulas[J]. Hydrological Processes,2007,21:2157-2163.

[20] 陆桂华,闫桂霞,吴志勇,等. 基于Copula函数的区域干旱分析方法[J]. 水科学进展,2010,21(2):188-193.

[21] 马秀峰. 游程概率统计原理及其应用[M]. 北京:科学出版社, 2011.

[22] 葛彩莲. 应用游程理论分析无定河流域气象干旱[J].水利科技与经济,2012,18:58-59.

[23] 王谦,陈景玲. 游程理论在河南省冬小麦干旱问题中的应用研究[J]. 河南农业大学学报,1994,2:136-143.

[24] 杨好周,梁忠民,胡义明,等. 游程理论在云南省干旱重现期分析中的应用[J]. 水电能源科学,2013,12:8-12.

[25] 左冬冬,侯威,颜鹏程,等. 基于游程理论和两变量联合分布的中国西南地区干旱特征研究[J]. 物理学报,2014,63(23):53-64.

[26] McKee T B, Doesken N J, Kleist J. The relationship of drought frequency and duration to time scales[A]. The 8th Conference on Applied Climatology[C]. California, 17-22 January 1993.

[27] Guttman N B. Comparing the Palmer Drought Index and the Standardized Precipitation Index[J]. Jawra Journal of the American Water Resources Association, 1998, 34(1):113-121.

[28] Herbst P H, Bredenkamp D B, Barker H M G. A technique for the evaluation of drought from rainfall data[J]. Journal of Hydrology, 1966,4:264-272.

[29] Shen H W, Guillermo Q T. Drought Analysis with Reservoirs Using Tree-Ring Reconstructed Flows[J]. Journal of Hydraulic Engineering, 1995,121(5):413-421.

[30] Mohan S, Rangacharya N C V. A modified method for drought identification[J]. Hydrological Science Journal, 1991,36(1):11-21.

[31] Zelenhastic E, Salvai A. A method of streamflow drought analysis[J]. Water Resources Research, 1987,23(1):156-168.

[32] Shiau J T, Hsieh W S. Recurrence analysis of hydrologic droughts of differing severity[J]. Journal of Water Resoures Plannning Management, 2001,127(1):30-40.

[33] 林宝山,曲焕云,白福春. 用K-S检验洛特卡定律著者群的取值范围[J]. 图书馆学研究,1996,6:61-64.

[34] Fu G T, David B. Copula-based frequency analysis of overflow and flooding in urban drainage systems[J]. Journal of Hydrology,2014,510:49-58.

[35] Zhang L, Singh V P. Bivariate rainfall frequency distributions using Archimedean copulas[J]. Journal of Hydrology, 2007,332:93-109.

Research on Drought Characteristics in China Based on the Revised Copula Function

CHEN Zaiqing1,2，HOU Wei2，ZUO Dongdong2,3，HU Jingguo1,2

(1.CollegeofPhysicsScienceandTechnology,YangzhouUniversity,Yangzhou225002,China;2.LaboratoryforClimateStudies,NationalClimateCenter,Beijing100081,China;3.CollegeofMathematicsScienceofYangzhouUniversity,Yangzhou225002,China)

Abstract:Based on the monthly precipitation of 613 meteorological stations in China during 1961-2010, the standardized precipitation index (SPI) was caculated, firstly. Then, the drought events were selected by using the run length theory, and the probability distribution fucnctions of drought intensity and drought duriation were tested by using K-S test. And on this basis the joint probability distribution function of dought intensity and drought duriation was established by using the Compula function, and the influence of the revised and unrevised drought duration distribution function on different types drought joint probability and recurrence peroid was contrastively analyzed. The results show that the drought intensity variable conformed to Gamma disttibution, while the drought duriation didn’t completely accord with the exponential function. Therefore, it was necessary to revise the drought duration distribution function so as to pass the K-S test. Under the revised drought duration distribution function condition, the joint probability of most drought types decreased, while that of a few increased, and the joint return peroid of different types drought increased. The difference of the maximum and minimum joint return peroid wasn’t obvious as the intensity of drought increased under the same drought duration, but that obviously enlarged as the drought duration increased under the same drought intensity.

Key words:drought; run length theory; Copula function; revision

中图分类号：P426.616

文献标识码：A

文章编号：1006-7639(2016)-02-0213-10

doi:10.11755/j.issn.1006-7639(2016)-02-0213

作者简介：陈再清(1990-),男,江苏淮安人,硕士研究生,主要从事极端天气气候事件及气候变化方面的研究. E-mail：zaiqingchen@126.com

基金项目：国家自然科学基金(41305056，41530531，41375069)和公益性行业(气象)科研重大专项 (GYHY201506001)共同资助

收稿日期：2015-09-08；改回日期：2015-11-17

陈再清，侯威，左冬冬，等.基于修订Copula函数的中国干旱特征研究[J].干旱气象，2016，34(2)：213-222, [CHEN Zaiqing, HOU Wei, ZUO Dongdong, et al. Research on Drought Characteristics in China Based on the Revised Copula Function[J]. Journal of Arid Meteorology, 2016, 34(2):213-222], doi:10.11755/j.issn.1006-7639(2016)-02-0213