基于混合Copula的ETF配对交易策略
2016-06-01沈银芳郑学东徐信喆
沈银芳, 郑学东, 徐信喆
(1.浙江财经大学 数据科学学院, 浙江 杭州 310018; 2.上海交通大学 安泰经济与管理学院, 上海 200052)
基于混合Copula的ETF配对交易策略
沈银芳1, 郑学东1, 徐信喆2
(1.浙江财经大学 数据科学学院, 浙江 杭州 310018; 2.上海交通大学 安泰经济与管理学院, 上海 200052)
摘要:配对交易是一种非常普遍的投资策略,被广泛应用于金融市场.距离法和协整法在配对交易策略中使用最普遍,然而,这2种方法只能描述股票之间的线性相关结构.本文基于3类基本的阿基米德Copula函数构成的混合Copula,定量刻画了资产之间的条件相关性,给出了新的配对交易策略,并将其运用于高频ETF市场.实证分析表明,新的策略可以捕获更多相依信息,得到更多的交易机会.
关键词:配对交易策略;混合copula;条件相关性;高频;ETF
SHEN Yinfang1, ZHENG Xuedong1, XU Xinzhe2
(1.SchoolofDateSciences,ZhejiangUniversityofFinanceandEconomics,Hangzhou310018,China; 2.AntaiCollegeofEconomics&Management,ShanghaiJiaoTongUniversity,Shanghai200052,China)
配对交易(pairs trading)的理念最早起源于20世纪20年代华尔街传奇交易员JESSE LIVERMORE的姐妹股票对(sister stocks)交易策略.20世纪80年代摩根士坦利公司成立了一支由TARTAGLIA领导的量化团队,专门开展配对交易的研究,并于1987年投入实战,当年盈利5 000万美元.经过多年研究和市场实战,配对交易的理论框架和配套交易系统都日臻完善.传统的配对交易方法见文献[1-3],具体如表1所示.最小距离法因无模型假设、操作简单、具有一定的盈利能力而得到广泛使用,然而正态性假设使得该方法的应用受限.同时上述传统交易策略均基于股票的线性相关性和对称性来研究价差序列.
Copula函数因其灵活性和优良性已成为相关性结构建模的标准工具,被广泛应用于金融领域.Copula函数全面描述了随机变量之间的对称、非对称、非线性和尾部相关性,因此Copula函数能全面刻画相关模式,而普通相关性度量很难完整描述那些由各类相关性组合而成的特殊相关模式.文献[4]最早将Copula函数应用于交易策略.文献[5-6]对股票日收益率数据,采用相关系数配对,并利用t-Copula,正态Copula和常见的阿基米德Copula函数拟合联合分布,根据Copula函数刻画的尾部相关系数得到配对交易策略.在国内,文献[7]利用Clayton Copula函数刻画期货合约日内价格序列之间的下尾部相关性,建立了基于Copula函数的程序化交易策略,并比较其在不同频率的分钟价格序列中的策略表现,年化收益率最高为23.61%.文献[8-9]通过实证得到协整关系,利用协整噪音获利.基于变系数的协整模型,文献[10]提出了利用残差的平稳过程进行套利的高频配对交易方法,并将此方法应用到ETF市场中.
表1传统的配对交易方法

Table 1 Traditional pairs trading methods
在高频环境下,金融资产之间非线性、非对称相关性和非正态性较低频更显著,由此,利用Copula方法构建高频环境下的配对交易策略应该更具优势.文献[8]在高频环境中引入了Clayton Copula函数,使用期望的成功概率作为门限,构造和释放资产价格波动的信号,最终建立了基于Copula函数的程序化交易策略,并在我国期货市场中进行实证分析.由于Copula函数能捕获金融资产之间的各种相关结构,抓住更多的交易机会,年化收益率应该比较高.然而从上述利用Copula方法的配对交易策略来看并非如此,主要原因在于所采用的Copula模型比较单一,导致相关结构的刻画不够全面,建仓和平仓条件还比较粗糙.鉴于此,本文运用混合Copula函数,定量刻画金融资产之间的条件相关性,讨论配对交易策略,并在高频ETF市场进行实证分析,从年化收益率、夏普率和最大回撤等指标来看,策略还是比较成功的.本文考虑ETF市场,是因为ETF在二级市场上买卖,仅需支付交易佣金,无交易印花税,而且目前许多券商,对利用ETF进行套利交易的客户,大多采用交易佣金下浮的优惠政策.本文假设投资者在交易之前已经持有了所需ETF种类的一定头寸,在高频套利交易期间发生的卖空为从已有的头寸中卖出,本文的收益是以几种ETF为基础的超额收益.
文章安排如下:首先,简要介绍混合Copula模型和基于混合Copula模型的新的配对交易策略;其次,选取流动性比较强的50ETF、180ETF和300ETF市场进行实证分析;最后是总结部分.
1模型
1.1混合Copula模型
Copula函数是一种将联合分布与其各自的边缘分布连接在一起的函数.阿基米德Copula函数可以刻画与实际情况更为接近的非对称、非线性和尾部相关性,而且不限制单个变量的边缘分布形式,因此,阿基米德Copula函数的建模方式比较灵活.最常见的阿基米德Copula函数为Clayton、Gumbel和Frank Copula函数.它们的具体形式分别为:
CClayton(u,v;θ)=(u-θ+v-θ-1)-1/θ,θ>0,
CGumbel(u,v;α)=exp(-[(-lnu)α+
(-lnv)α]1/α),α≥1,
CFrank(u,v;β)=-ln(1+(e-βu-1)(e-βv-1)/
(e-β-1)),β≠0,
其中,0≤u,v≤1.Clayton、GumbelCopula函数分别对变量在其下尾部和上尾部的分布变化十分敏感,适用于描述金融市场之间的下尾相关和上尾相关特性,FrankCopula函数可以用于描述具有对称相关结构的变量之间的相关关系.于是由Clayton、Gumbel和FrankCopula函数的线性组合构成的混合Copula:CCGF(u,v;Φ)=λ1CClayton(u,v;θ)+λ2CGumbel(u,v;α)+
λ3CFrank(u,v;β),
(1)
可以反映金融市场相关性变化的各种情形,是研究多个资产价格在上升和下跌时出现关联性变化的理想工具,其中0≤λ1,λ2,λ3≤1,λ1+λ2+λ3=1,Φ=(λ1,θ;λ2,α;λ3,β).
本文基于上述混合Copula模型构建配对交易策略,首先由混合Copula函数捕捉资产价格上升和下跌的相关性条件,然后根据上升和下跌的相关性强弱进行开仓和平仓交易,最后将交易的收益率换算成年化收益率,计算夏普率、最大回撤和胜率.
1.2配对交易策略模型
基于Clayton、Gumbel和FrankCopula构成的混合Copula函数的配对交易策略,构建步骤如下:
(i)在选定的样本期T内,假设2资产X,Y的价格序列分别为PX(t),PY(t),其边际分布用各自的经验分布近似,得到均匀分布序列:U(t)=FX(PX(t)),V(t)=FY(PY(t)),t∈T.
(2)
则Clayton、Gumbel和FrankCopula构成的混合Copula函数:
CCGF(U(t),V(t);Φ)=λ1CClayton(U(t),V(t);θ)+λ2CGumbel(U(t)),V(t);α)+λ3CFrank(U(t),V(t);β).
(3)
利用极大似然估计法,估计上述混合Copula函数的相关参数:
若设u=FX(x),v=FY(y),则
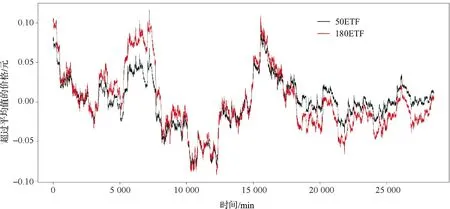
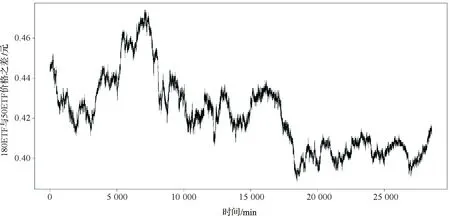
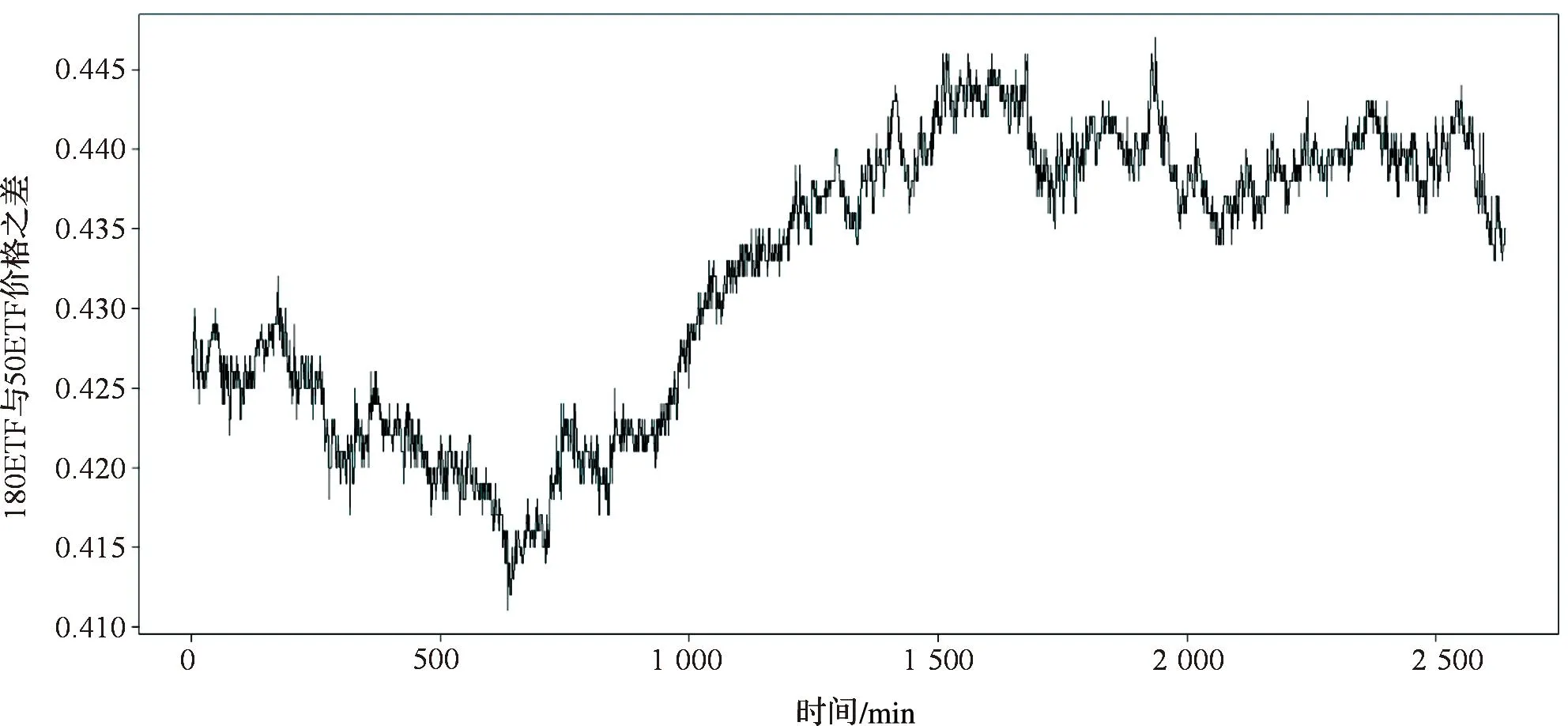
P{PX(t) P{U(t) (4) 又由Copula函数的性质得 P{U(t) ∂CCGF(U(t),v)/∂U(t)|U(t)=u, (5) P{V(t) ∂CCGF(u,V(t))/∂V(t)|V(t)=v. (6) (ii)开仓点:若 P{U(to1) P{V(to1) (7) 说明to1时刻资产X的价格相对高估,而资产Y的价格相对低估,即资产X的价格很可能降低,而资产Y的价格很可能上升,则在to1时刻开仓卖出X买进Y. 同理当 P{V(to2) P{U(to2) (8) 说明to2时刻资产Y的价格相对高估,而资产X的价格相对低估,即资产Y的价格很可能降低,而资产X的价格很可能上升,则在to2时刻开仓卖出Y买进X. (iii)平仓点:在to1时刻开仓后,若 P{U(tc1) P{V(tc1) (9) 即在tc1时刻2资产的价格既不低估也不高估,于是在tc1时刻卖出Y,买进X平仓.同理,在to2开仓后,若 P{V(tc2) P{U(tc2) (10) 即在tc2时刻2资产的价格既不低估也不高估,于是在tc2时刻卖出X,买进Y平仓. (iv)止损点:本文中使用日内价格1min数据,取止损点为S=240,即若开仓后一日内没有发现平仓点,则强行平仓. 2实证分析 以中国金融市场中的ETF为实证对象.根据流动性,分别选取50ETF、180ETF和300ETF.数据频率为1min,使用数据的日期为2014年1月2日到2014年6月30日,每支ETF含28 560个数据.在计算中,买卖交易均扣除手续费,手续费率为0.03%,同时设初始资金ASSET(0)=1(万元),每次开仓交易时由拥有的资金决定交易量,具体为t时刻开仓,资金量ASSET(t)=VX(t)×PX(t)=VY(t)×PY(t), (11) 其中VX(t),VY(t),PX(t),PY(t)分别表示t时刻资产X,Y的交易量和价格. 2.150ETF和180ETF配对的套利分析 从图1中可以观察到,50ETF和180ETF价格序列呈现很强的协整关系.图2和3反映2点:一方面,50ETF和180ETF价差序列开始剧烈波动,大约18 000样本点之后变化趋缓;另一方面,大约在15 000样本点之前,180ETF比50ETF更显著超过其平均价格,15 000样本点之后,50ETF比180ETF更显著超过其平均价格.然而上述方法只提供简单的线性关系,本文将利用混合Copula模型全面刻画2价格序列之间的条件相关性,进一步进行配对交易策略分析.首先分别将取样时间段内每月上半月(15日以前,含15日)或每月下半月(15日以后,不含15日)的价格数据作为训练样本,估计上述混合Copula函数的参数,然后去拟合当月下半月或次月上半月的价格数据,构建策略模型. 图1 50ETF和180ETF价格序列图Fig.1 Prices of 50 ETF and 180 ETF 图2 50ETF、180ETF超过各自平均价格部分的价格序列图Fig.2 Prices of 50 ETF and 180 ETF more than means 图3 50ETF、180ETF价差序列图Fig.3 Price spread between 50 ETF and 180 ETF 表250ETF和180ETF的混合Copula函数参数估计结果 Table 2 Parameters estimation of mixture Copula between 50ETF and 180ETF 在按上述方案拟合50ETF和180ETF价格数据时,样本期内出现了混合Copula函数的11组参数,具体见表2.由表2知,50ETF和180ETF的相关性在不断变化,2014年1月上半月拟合的Copula模型中Clayton Copula函数的权重系数λ1几乎为0,而Gumbel、Frank Copula函数的权重系数λ2和λ3显著不为0,说明2014年1月上半月50ETF和180ETF市场的上尾部和对称相关性比较显著,下尾部相关性不显著,几乎不存在下尾部相关性,而下半月下尾部和上尾部相关性显著,对称相关性不显著;2月上半月3种相关性都显著存在,下尾部相关性更突出,2月下半月3种相关性都存在,但是上、下尾部相关性不是特别显著,对称相关性非常显著.各Copula参数的估计值则表明,50ETF和180ETF价格序列之间存在较强的条件正相关.若在整个取样时间段内利用相同参数和同种类型的Copula函数,拟合效果必定会受损,上述“滚动”的混合Copula模型可以较准确地捕捉到50ETF和180ETF市场之间的各种相关模式,从而全面刻画金融市场之间的相关结构. 图4 50ETF和180ETF的Copula拟合图Fig.4 Copula fitting of 50ETF and 180ETF 图6 50ETF和180ETF原始价格序列散点图Fig.6 Scatter diagram of 50ETF and 180ETF’s original prices 图4~6分别为50ETF和180ETF在2014年1月16~30日(即2 401~5 040样本点)的混合Copula模型拟合图、价格序列经验分布变换后散点图和原始价格序列散点图,可以观察到混合Copula模型、经验分布变换以及原始价格序列所揭示的分布规律基本一致. 在构建交易策略时,50ETF和180ETF 1月下半月的条件概率变化如图7所示.180ETF价格序列条件概率值开始非常高,接近1,而50ETF价格序列条件概率值则非常低,接近0,故认为180ETF价格高估的可能性大,即价格很可能趋低,对应地,50ETF价格低估的可能性很大,即价格很可能趋高,因此首先考虑开仓卖出180ETF,买进50ETF,随后当180ETF序列条件概率值不超过0.5,而50ETF序列条件概率值不低于0.5时,进行反向操作即平仓处理,完成1次配对交易.再来看50ETF和180ETF条件概率之差序列图图8以及价差序列图图9,2图趋势基本一致,条件概率之差波动更显著,尤其在280~1 000样本点,条件概率之差起伏明显,而价格之差变化不显著,这是因为价格差只考虑了价格序列之间的线性关系,而由混合Copula模型得到的条件概率之差还能充分利用2价格序列之间的非线性、非对称性和尾部相关性,从而能更细致准确地刻画价格序列的变化,发现更多的交易机会. 图7 50ETF和180ETF的条件概率变化图Fig.7 Conditional probabilities of 50ETF and 180ETF’s 图8 50ETF和180ETF的条件概率之差序列图Fig.8 Spread of conditional probabilities between 50ETF and 180ETF 图9 50ETF和180ETF的价差序列图Fig.9 Price spread between 50ETF and 180ETF 盈利的稳定性对一个交易策略至关重要.夏普率通常作为衡量策略稳定性的指标,由于其在6以上的策略均非常稳健,由表3知,本文提出的新的交易策略亦非常稳健.另外,还验证了每次交易的收益率序列为平稳序列,ADF检验的p值为0.014 52,也说明策略的稳定性.同时套利组合获得的累计收益率如图11所示,平稳向上的累计收益率曲线同样说明了策略的可行性与稳定性. 图10 50ETF和180ETF收益率序列图Fig.10 Rate of return of 50ETF and 180ETF 图11 50ETF和180ETF累计收益率序列图Fig.11 Cumulative rate of return of 50ETF and 180ETF 2.2180ETF和300ETF配对,50ETF和300ETF配对的套利分析 对180ETF和300ETF配对、50ETF和300ETF配对构建交易策略,用同样的方法进行模型拟合和参数估计,2种套利均有良好的表现,表3列出了本文所涉及的3种配对组合的套利表现. 表33种配对组合的套利表现 Table 3 Arbitrage performance of three pairs 由表3知,新策略发现的交易次数与文献[10]相当,但后者使用的是间隔30 s的数据,数据量大约是本文的2倍,这充分说明本文所提出的策略捕获了更多的交易机会.同时,本文还验证了180ETF和300ETF配对、50ETF和300ETF配对的交易收益率序列均为平稳序列,ADF检验的p值均小于0.01,进一步说明了本文策略的稳定性. 3结论 提出了基于混合Copula函数的新的配对交易策略模型,并将其应用于中国金融市场3支ETF-50ETF、180ETF和300ETF两两配对组成的3个投资组合上,得到了令人满意的套利结果,可供交易者和相关机构参考.本文在以下几方面尚需改进:(1)取条件概率临界值为0.9和0.1,止损点为240,带有一定的主观性,需进一步探求其与金融市场及其数据频率的关系;(2)由于金融市场的相依性是动态变化的,可能出现高低交替波动的情况,需要引入时变相关Copula模型和马尔可夫结构转换Copula模型,讨论资产之间的动态时变条件相关结构,进而得到动态时变配对交易策略模型.有待进一步研究. 参考文献(References): [1]VIDYAMURTHY G. Pairs Trading: Quantitative Methods and Analysis[M]. NewYork:John Wiley and Sons,2004. [2]ELLIOTT R, VAN DER HOEK J, MALCOLM W. Pairs trading[J]. Quantitative Finance,2005,5(3):271-276. [3]GATEV E, WILLIAM N, GOETZMANN K, et al. Pairs trading: Performance of a relative-value arbitrage rule[J]. The Review of Financial Studies,2006,19(3):797-827. [4]FERREIRA L. New tools for spread trading[J]. Futures,2008,37(12):38-41. [5]LIEW R Q, WU Yuan. Pairs trading: A Copula approach[J]. Journal of Derivatives and Hedge Funds,2013,19(1):12-30. [6]STANDAER Y, MARAIS D, BOTHA I. Trading strategy with Copulas[J]. Journal of Economics and Financial Sciences,2013,6(1):83-108. [7]张戈,程棵,陆凤彬,等.基于Copula函数的程序化交易策略[J].系统工程理论与实践,2011,31(4):599-605. ZHANG Ge, CHENG Ke, LU Fengbin, et al. Program trading strategy based on Copula functions[J]. Systems Engineering-Theory and Practice,2011,31(4):599-605. [8]张连华.基于高频数据的股指期货期现统计套利程序交易[J].计算机应用与软件,2011,28(9):93-95. ZHANG Lianhua. High frequency data based stock index futures present statistical arbitrage program trading[J]. Computer Applications and Software,2011,28(9):93-95. [9]陈怡.统计套利策略在我国分级基金市场的尝试[J].科学技术与工程,2012,12(3):724-729. CHEN Yi. The trading strategy of split-funds based on statistical arbitrage[J]. Science Technology and Engineering,2012,12(3):724-729. [10]陈实,吴述金,郑伟安.中国市场ETF套利研究[J].华东师范大学学报:自然科学版,2013(5):144-151. CHEN Shi, WU Shujin, ZHENG Weian. ETF arbitrage research on China financial markets[J]. Journal of East China Normal University:Natural Science,2013(5):144-151. Pairs trading strategy of ETF based on mixture Copula. Journal of Zhejiang University(Science Edition), 2016,43(3):271-278 Abstract:Pairs trading is a well-acknowledged speculative investment strategy that is widely used in the financial markets. Distance and co-integrated methods are the most commonly implemented pairs of trading strategies. However, these two approaches are only able to describe the linear dependency structure between stocks. A new pairs of trading strategies based on mixture Copula method is produced. Three elementary Archimedean Copula families are used to construct mixture Copulas, which describe the conditional dependence between assets. In the high frequency exchange traded fund (ETF) market, it is deemed to catch more dependence informations and generate more trading opportunities. Key Words:pairs trading strategy; mixture copula; conditional dependence; high frequency; ETF 中图分类号:O 213;O 211.9 文献标志码:A 文章编号:1008-9497(2016)03-271-08 作者简介:沈银芳(1978-),ORCID:http:r/orcid-org/0000-0003-2080-6530,女,博士研究生,副教授,主要从事金融时间序列分析研究,E-mail:fsilver@163.com. 基金项目:浙江省自然科学青年基金资助项目(LQ14G010007);全国统计科学研究项目(2015LY45);2015浙江省统计研究重点课题“时变混合Copula模型的构建选择及其应用”;教育部人文社科基金资助项目(12YJC910011). 收稿日期:2015-02-02. DOI:10.3785/j.issn.1008-9497.2016.03.004