基于频域校正的快速长时间积累算法
2016-06-01王泽玉卢云龙陈洪猛曹润清
王泽玉,李 明,卢云龙,陈洪猛,曹润清,左 磊,张 鹏
(西安电子科技大学 雷达信号处理国家重点实验室,西安 710071)
基于频域校正的快速长时间积累算法
王泽玉,李明,卢云龙,陈洪猛,曹润清,左磊,张鹏
(西安电子科技大学 雷达信号处理国家重点实验室,西安 710071)
摘要:针对长时间积累过程中回波信号出现的距离徙动和多普勒走动问题,提出一种基于 频域校正的快速长时间积累算法。该算法首先利用Radon-Ambiguity 变换对脉压以后的回波信号 进行加速度估计,用得到的估计值构造加速度补偿因子消除距离弯曲和多普勒走动,然后选取回 波包络之间的相关系数作为代价函数对目标的速度进行估计,用得到的估计值构造速度补偿因子 消除距离走动。仿真结果验证了该算法的有效性。
关键词:长时间积累; 距离徙动; 多普勒走动; 补偿因子; 频域校正
0引言
长时间积累技术能改善回波的信噪比,是现代雷达提高检测性能的一种有效途径[1]。 但随着积累时间的增加,运动目标回波容易产生距离徙动(包括距离走动和距离弯曲)和多普勒走动现象,使得目标能量扩散,回波得不到有效积累[2-5]。 因此,如何进行有效的包络补偿和多普勒补偿是长时间积累技术亟待解决的问题[6-8]。
针对运动目标长时间积累过程中出现的距离走动问题,文献[9]提出一种基于约当傅立叶变换(Radon-Fourier Transform,RFT)的运动目标检测方法; 文献[10]提出一种基于分时处理的相干积累及Keystone变换校正相结合的距离徙动实时相干积累算法,实现高速目标的有效检测; 文献[11]提出一种改进Keystone变换算法。 但以上算法只适用于目标作匀速运动时的情况,当目标作匀加速运动并在长时间积累过程中产生距离徙动和多普勒走动时,这些算法均失效。 针对这个问题,文献[12]将Keystone变换与Wigner-Hough变换进行结合,提出一种用于机载相控阵预警雷达实现高速空中机动目标检测的新方法。 然而当目标速度较大,产生多普勒模糊时,该算法需要对模糊数进行搜索,计算量较大,并且采用Wigner-Hough变换对加速度进行搜索,计算量进一步加大。
为减小计算量,本文提出一种基于频域校正的快速长时间积累算法,该算法首先采用约当模糊变换(Radon Ambiguity Transform, RAT)估计目标的加速度,构造加速度补偿因子,补偿加速度引起的距离弯曲和多普勒走动,再选取计算量小的代价函数对目标速度进行搜索,构造速度补偿因子,补偿速度引起的距离走动。 实验结果表明本文算法能有效实现包络补偿和多普勒补偿,且与文献[12]相比,计算量明显减少。
1回波信号模型
(1)


(2)
(3)
2基于频域校正的快速长时间积累算法

(4)

由以上分析可知,距离徙动和多普勒走动是由目标速度和加速度引起的回波相位变化,因此,本文构造相位补偿因子对加速度相位项和速度相位项进行补偿,从而消除距离徙动和多普勒走动。
2.1加速度相位项补偿
信号s(t)的模糊函数定义为
AFs(τ,ξ)=∫-∞∞s(t+τ/2)s*(t-τ/2)e-j2πξtdt
(5)
式中: []*为共轭运算; (τ,ξ)平面为模糊域。 当信号s(t)为线性调频信号时,s(t)的模糊函数为
AFs(τ,ξ)=A2δ(ξ-μ0τ)exp(j2πf0τ)
(6)
式中: f0为中心频率; μ0为调频率。 对线性调频信号的模糊函数取模以后作Radon变换,得到

(7)
由式(7)可知,当观测信号中含有调频率为μ0的线性调频信号时,检测器在μ=μ0点出现峰值,可通过峰值的位置估计线性调频信号的调频率。
由式(4)可知,当频率f为一个定值时(f=fconst,即选定一个距离单元),信号Sr(fconst,tm)是关于方位慢时间的线性调频信号。 该线性调频信号的调频率是目标加速度的函数。 因此,可以对Sr(fconst,tm)进行RAT来检测该线性调频信号的调频率,从而估计出运动目标的加速度。
设对信号Sr(fconst,tm)进行RAT以后,搜索得到的峰值对应的弧度为θ0,则θ0对应的线性调频信号的归一化调频率可以表示为[14]
(8)
式中:M为脉冲数;Tr为脉冲重复周期。 同时,由式(4)可计算得理论上线性调频信号Sr(f,tm)对应的归一化调频率为
(9)
联立式(8)~(9)可以求得运动目标加速度的估计值为
(10)

(11)
由式(11)可以明显看出,加速度引起的距离弯曲和多普勒走动均得到补偿,而且由于RAT只是模糊平面上的一维搜索,与Wigner-Hough变换法的二维搜索相比,计算量大大减少[14-15]。 但是回波距离走动的指数相位项仍然存在,接下来需要对目标速度引起的距离走动进行补偿。
2.2速度相位项补偿
为了对距离走动进行校正,本文选取第一个脉冲和最后一个脉冲的相关系数为代价函数,对目标速度进行搜索,然后构造关于速度的补偿因子项,来完成距离走动校正。
将速度范围(目标速度一般不超过1 000 m/s)以相等的步长量化为N个值(步长Δv≤ΔR/2T。 其中,ΔR为距离分辨单元,T为积累时间。 同时为了减少运算量,步长不应该选取的太小,即步长Δv的选取是量化误差和计算量的折衷),然后根据N个速度值确定N个相位补偿因子进行搜索补偿,具体步骤如下所示:
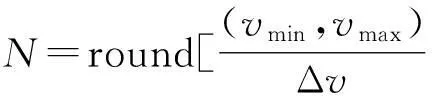



本文通过构造两个补偿因子来实现包络补偿和多普勒补偿,为获得补偿因子,对运动目标的加速度和速度进行估计,具体实现流程如图1所示。

图1基于频域校正的匀加速目标长时间积累算法流程图
3仿真实验
雷达仿真参数的设置如表1所示。

表1 雷达仿真参数
目标参数: 设目标速度为690 m/s; 加速度为50 m/s2; 初始距离为10.5 km; 信噪比SNR(脉压前)为0 dB。 目标的速度搜索范围选取为(0 m/s, 1 000 m/s),速度的搜索步长选为18 m/s。
将1 024个脉冲回波信号进行频域脉冲压缩,并变换到时域以后得到的结果如图2所示,由图可以看出,由于在长时间积累过程中有速度和加速度的存在,回波存在严重的距离徙动。 对图2的结果直接进行相参积累,得到的结果见图3。 由图3可以看出,直接进行相参积累时,能量在多普勒域展宽严重,积累效果很差。 因此,必须进行加速度和速度的估计并对回波信号进行补偿。

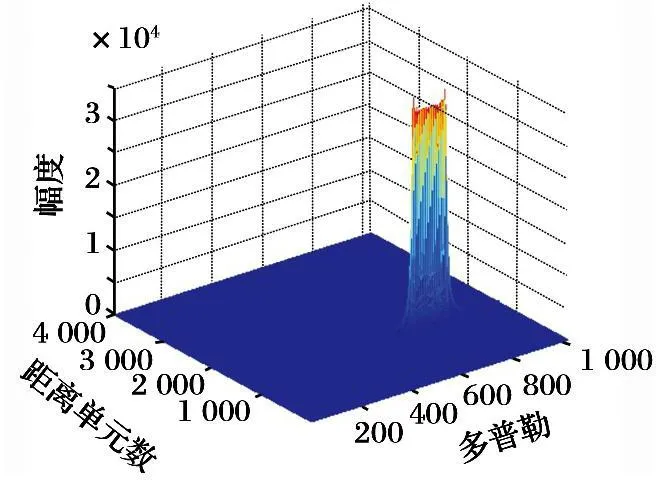
图2 原始脉压回波数据
图3直接相参积累结果
频域脉压信号在一个距离单元上进行RAT得到的结果如图4(a)所示。 图中出现一个明显的峰值,将峰值对应的角度代入式(10),计算得到加速度的估计值。 对频域信号进行加速度相位项补偿后,利用N个量化速度进行速度补偿,得到N个量化速度对应的代价函数如图4(b)所示。 图中相关系数的峰值对应的速度即为速度的估计值。

图4频域补偿因子搜索示意图
文献[12]的算法与本文算法对比的结果如图5(a)~(d)所示。 图5(a)~(b)分别为利用文献[12]算法和利用本文算法补偿后的时域回波结果,由图可知,两种算法补偿后包络都基本对齐。 此时分别对两种算法校正后的回波信号作相参积累,得到的结果如图5(c)~(d)所示。 与图3对比可知,两种算法校正后能量聚集到一个距离单元,多普勒扩散也已基本消除,积累效果明显改善。 实验表明,两种算法均能有效地校正加速度和速度引起的距离徙动和多普勒走动。



图5 长时间积累结果对比
表中RAT为RAT算法;WH为Winger-Hough算法;N为快时间采样点数;M为脉冲积累数;L为2的整数幂次,且有L>2M-1;S为搜索次数。 Winger-Hough算法是时频平面的二维搜索,而RAT算法是模糊平面的一维搜索。 因此,由仿真结果和算法复杂度分析可知,本文算法在有效校正距离徙动和多普勒走动的情况下,明显减少计算量。


图6长时间积累结果对比
由图6(a)可知,随着信噪比的增加,目标加速度的均方误差呈下降趋势,且RMSE均不大于0.12 m/s2。 由图6(b)可知,随着信噪比的增加,目标速度的RMSE下降,且当信噪比大于 -7 dB时,目标速度的RMSE为6 m/s并保持稳定。 说明本文算法在低SNR条件下具有一定的稳健性。
4结论
本文针对长时间积累算法计算量较大的问题,提出一种不需要考虑多普勒模糊的频域校正快速算法。 该算法通过RAT对加速度进行一维搜索,构造加速度补偿因子项消除加速度引起的距离弯曲和多普勒走动; 以回波之间的相关系数为代价函数对速度进行搜索,构造速度补偿因子项消除速度引起的距离走动。 仿真结果表明,本文算法能有效地实现包络补偿和多普勒补偿,并具有较小的计算量,因而更加适合工程应用。
参考文献:
[1] 赵永波, 周晓佩, 王娟. 一种用于弱信号检测的广义Keystone变换算法[J]. 西安电子科技大学学报, 2013, 40(2): 98-102.
[2] 叶春茂, 鲁耀兵, 宋建社, 等. 一种ISAR目标转动补偿及图像尺寸标定方法[J]. 电子学报, 2014, 42(3): 611-615.
[3] Su Junhai, Xing Mengdao, Wang Genyuan, et al. High-Speed Multi-Target Detection with Narrowband Radar[J]. IET Radar Sonar and Navigation, 2010, 4(4): 595-603.
[4] 张卫杰, 高昭昭, 许博, 等. 基于Keystone 变换的警戒雷达信号处理[J]. 系统工程与电子技术, 2011, 33(9): 2007-2011.
[5] 宁夏, 叶春茂, 杨健. 一种基于时频匹配的长时间相干积累器设计[J]. 系统工程与电子技术, 2013, 35(11): 2275-2282.
[6] Yang Jun, Sun Guangcai, Xing Mengdao, et al. Squinted TOPS SAR Imaging Based on Modified Range Migration Algorithm and Spectral Analysis[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(10): 1707-1711.
[7] 郑纪彬, 符渭波, 苏涛, 等. 一种新的高速多目标检测及参数估计方法[J]. 西安电子科技大学学报, 2013, 40(2): 82-88.
[8] Qian Jiang, Lv Xiaolei, Xing Mengdao, et al. Motion Parameter Estimation of Multiple Ground Fast-Moving Targets with a Three-Channel Synthetic Aperture Radar[J]. IET Radar Sonar and Navigation, 2011, 5(5): 582-592.
[9] Xu Jia, Yu Ji, Peng Yingning, et al. Radon-Fourier Transform for Radar Target Detection, I: Generalized Doppler Filter Bank[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(2): 1183-1202.
[10] 关欣, 胡东辉, 仲利华, 等. 一种高效的外辐射源雷达高径向速度目标实时检测方法[J]. 电子与信息学报, 2013, 35(3): 581-588.
[11] 王娟, 赵永波. 一种改进的Keystone 变换算法及其在微弱信号检测中的应用[J]. 航空兵器, 2011(5): 3-6.
[12] 吴仁彪, 贾琼琼, 李海. 机载雷达高速空中机动目标检测新方法[J]. 电子学报, 2013, 41(1): 86-90.
[13] 保铮, 邢孟道, 王彤. 雷达成像技术[M]. 北京: 电子工业出版社, 2005.
[14] 苏军海, 李亚超, 邢孟道, 等. 采用Radon模糊变换的宽带雷达多目标检测方法[J]. 西安交通大学学报, 2009, 43(4): 85-89.
[15] Sharif R, Abeysekera S S. Efficient Wideband Signal Parameter Estimation Using a Radon-Ambiguity Transform Slice[J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(2): 673-688.
[16] Grossi E, Lops M, Venturino L. A Novel Dynamic Programming Algorithm for Track-before-Detect in Radar Systems[J]. IEEE Transactions on Signal Processing, 2013, 61(10): 2608-2619.
A Fast Long-Time Accumulation Algorithm Based on Frequency-Domain Correction
Wang Zeyu, Li Ming, Lu Yunlong, Chen Hongmeng, Cao Runqing, Zuo Lei, Zhang Peng
(National Key Laboratory of Radar Signal Processing, Xidian University,Xi’an 710071,China)
Abstract:In order to solve range migration and Doppler walk caused by target motion during long-time coherent integration period, a novel fast algorithm based on frequency-domain correction is proposed. The Radon-Ambiguity transformation is utilized to estimate the acceleration and the acceleration compensation factor is constructed to correct range bend and Doppler walk. Then the relevance coefficient between the two echoes is used to estimate the velocity,and the velocity compensation factor is constructed to correct range walk. The simulation results prove the effectiveness of the proposed algorithm.
Key words:long-time coherent integration; range migration; Doppler walk; compensation factor; frequency-domain correction
中图分类号:TN958. 5
文献标识码:A
文章编号:1673-5048( 2016) 02-0061-05
作者简介:王泽玉(1990-),女,河南许昌人,博士研究生,研究方向为雷达微弱目标检测。
基金项目:国家自然科学基金项目(61271297; 61272281; 61301284); 国防预研基金项目(9140A07020913DZ01001)
收稿日期:2015-08-06
DOI:10.19297/j.cnki.41-1228/tj.2016.02.012
