IEEE30节点系统电压/无功优化
2016-05-31张俊张安安
张俊 张安安


摘 要:文中以IEEE30节点标准电网为基础,用Matpower完成了该电网模型的潮流分析。同时基于潮流分析结果,采取改变网络中无功功率分布调压、改变发电机端电压调压、改变变压器变比调压三种电力系统的主要调压措施来对电压偏移较大的节点进行了无功优化,最后分析了电压调整后的Matpower潮流结果,并得出了定性结论。
关键词:潮流计算;Matpower;电压调整;无功优化;IEEE30
中图分类号:TM712 文献标识码:A 文章编号:2095-1302(2016)05-00-03
0 引 言
随着电力系统规模的不断扩大,潮流问题方程阶数越来越高,对计算速度的要求也不断提高,基于Matlab潮流计算研究近年来取得了长足的发展,在保证电力系统供电可靠性和电能质量的前提下,尽可能的提高潮流计算效率,降低人力资源消耗,从而提高电力系统运行的经济性[1-5]。
由于电力系统中节点数目多,网络结构复杂,负荷分布不均匀,当节点的各负荷变动时,会引起各节点电压的波动[6]。要使各节点电压维持在额定值是不可能的。所以,电力系统调压的任务就是在满足各负荷正常需求的条件下,使各节点的电压偏移在允许范围之内[7]。
1 电力系统潮流计算
潮流计算是电力系统规划、运行的基本研究方法,其任务是要在已知(或给定) 某些运行参数的情况下,计算出系统中的全部参数,包括各母线电压的大小、相位,各发电机负荷的功率、电流以及各个变压器和线路等元件所通过的功率、电流和损耗[1-5]。
1.1 Matpower选项
Matpower是一个基于Matlab的M文件的组建包,用来解决电力潮流和优化潮流的问题[8]。Matpower所用的所有数据文件均为Matlab的M文件或者MAT文件,用来定义和返回变量baseMVA、bus、branch、gen等。
baseMVA 变量是一个标量,用来设置基准容量。若计算中采用有名值,可以根据需要设置,如100 MVA;若计算中采用标么值,一般设置为1。
bus变量是一个矩阵,用来设置电网中各母线参数,其格式为bus_ i、type、Pd、Qd、Gs、B s、area、Vm、Va、baseKV、zone、Vmax、Vmin。type用来设置母线类型,1为PQ节点母线,2为PV节点母线,3为平衡(参考)节点母线。
branch变量是一个矩阵,用来设置电网中各支路参数,其格式为fbus、tbus、r、x、b、rateA、rateB、rateC、ratio、angle、status。fbus和tbus用来设置该支路由起始节点(母线)编号和终止节点(母线)编号。r、x和b用来设置该支路的电阻、电抗和充电电纳。ratio用来设置该支路的变比,如果支路元件仅仅是导线为0;如果支路元件为变压器,则该变比为fbus侧母线的基准电压与tbus侧母线的基准电压之比。
gen变量也是一个矩阵,用来设置接入电网中的发电机(电源)参数,其格式为bus、Pg、Qg、Qmax、Qmin、Vg、mBase、status、Pmax、Pmin。mBase用来设置接入发电机(电源)的功率基准,如为缺省值,就是baseMVA变量的值。
1.2 潮流计算结果与分析
Matpower潮流计算结果得出:IEEE30系统的构成(母线数、发电机数、在用发电机数、总负荷、固定负荷、可分配负荷、分流、分支和变压器);容量(总发电容量、在线容量和实际发电量);功率(负荷功率、固定功率、可分配功率和分流(注入)功率)的分布情况,及在潮流分析计算时最关心的总的有功、无功损耗(分别为17.56 MW和67.69 MVA),电压幅值、相角的最大最小值及对应的节点序号。幅值:最大(11节点,1.082),最小(30节点,0.992);相角:最大(1节点,0.00度),最小(30节点,-17.64度);最大有功、无功损耗的值及出现的支路信息(1~2支路的有功、无功损耗均最大,分别为5.21 MW和15.61 MVA)。
1.3 电压偏移
网络中某点的实际电压同网络该处的额定电压之差称为电压偏移[9],可以用额定电压的百分数表示:
电压偏移(%)=(U-UN)/UN ×100%
根据实际情况选用标么值进行计算,本系统选择1节点为参考节点(Vn=1.060),为减少计算量,提高效率,由Matpower潮流结果找出电压幅值最大最小的点,分别为节点11和30,计算其电压偏移如下:
节点11(电压幅值最大):
由计算可知,节点11电压偏移较小,但节点30电压偏移较大,在以后调压时应更多的考虑节点30的电压情况。
2 电力系统无功和电压调整
负荷的无功功率随电压的降低而减少,要想保持负荷端电压水平,就得向负荷供应所需要的无功功率。所以,电力系统的无功功率必须保持平衡,即无功功率电源发出的无功功率要与无功功率负荷和无功损耗保持平衡。这是维持电力系统电压水平的必要条件[10,11]。
电力系统主要的调压措施如下[12]:
(1)改变发电机端电压调压;
(2)改变变压器变比调压;
(3)改变网络中无功功率分布调压;
(4)改变线路参数调压。
2.1 并电容器调压
并联电容器通过改变网络中无功功率的分布达到调压的目的。并联电容器因其简单方便、经济灵活且适用范围广,是广泛使用的调压方式。
2.1.1 并电容器调压原理
图1所示为具有无功补偿的系统图。
其中,K=Ut/UrN为变压器变比,Ut为变压器高压测分接头的电压,UrN为变压器低压绕组的额定电压。
2.1.2 并电容器调压结果分析
由于无具体调压要求,所以参考用式(1)算出的部分电压偏移结果,在电压最低点,即30节点处并一5 Mvar的电容器进行调压。
定性分析图2可知,1~13节点(个别节点除外)在并电容器调压前后的电压幅值几乎不改变,从14节点起,至30节点,并电容器调压前后的电压幅值的改变量开始明显,并随着节点序号的增加,电压幅值改变量不断增加且为正增量,在30节点处电压幅值差值达到最大。
图2 并电容器前后的电压幅值图
2.2 改变发电机端电压调压
改变发电机端电压是一种不需要耗费投资,且是最直接的调压方法,应首先考虑采用。发电机的电压调整借助于调整发电机的励磁电压,以改变发电机转子绕组的励磁电流,就可以改变发电机定子端电压。利用发电机调压范围在发电机额定电压的±5%,能够以额定功率运行[1-4]。
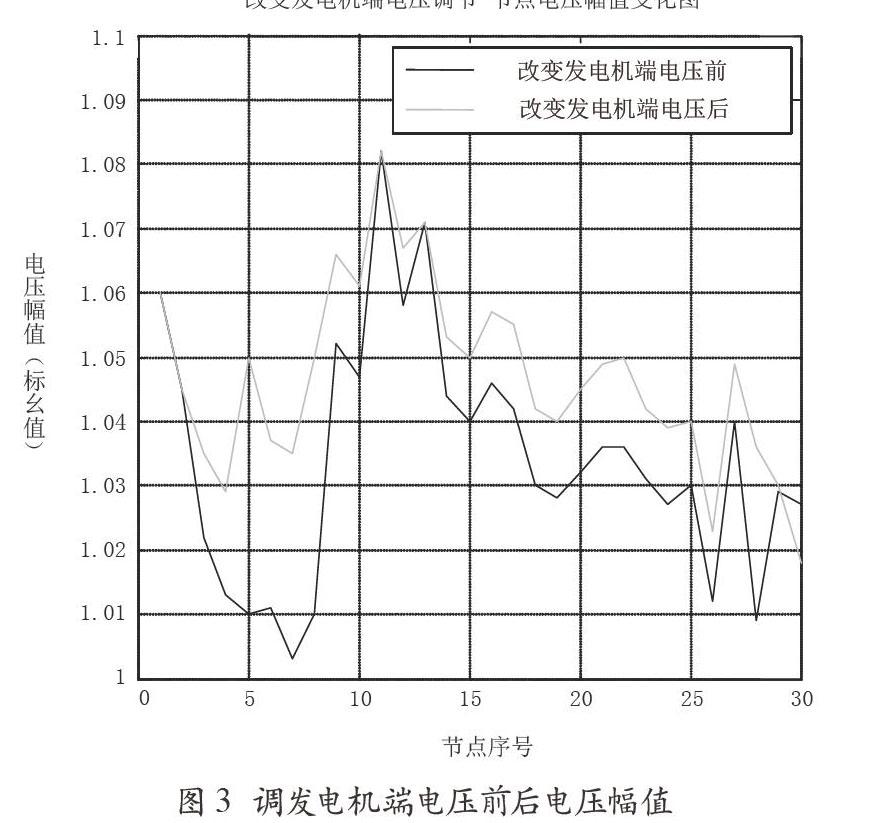
由于无具体调压要求,为提高电压最低点(即30节点处)的电压幅值,采用提高发电机节点电压较低的5、8节点处的电压,将其由原来的1.01提高到1.05。
定性分析图3可知,将5、8节点处的电压由原来的1.01提高到1.05后,几乎所有节点的电压幅值与初始值相比都发生了较大幅度的增加。
2.3 改变变压器变比调压
改变变压器变比调压虽然是一种寻常方法,但其先决条件是电网的无功电源容量充裕。如果电网的无功电源容量不足,采用变压器调压,虽然可能提高局部电网的电压水平,但也有可能降低主电网的电压水平,不利于全网的电压稳定,这是因为改变变压器变比,相对于在回路中串联了一附加电势,从而改变了电网的无功功率分配[3,4]。
选取电压幅值最小的30节点为调压对象,改变(增大和减小)与30节点直接相连的27~28节点变压器的变比。
(1)变比(28:27)由0.968升高为0.975。
图3 调发电机端电压前后电压幅值
定性分析图4可知,将变压器变比(28:27)由0.968升高为0.975后,从节点序号23开始,直到节点30,电压幅值有较为明显的小幅度下降,其余节点的电压幅值未发生变化或变化不明显。
结论:对于降压变压器(变比小于1)升高变比(不超过1)后,电压幅值降低。
图4 升变压器变比前后的电压幅值图
(2)变比(28:27)由0.968降低为0.95。
定性分析图5可知,将变压器变比(28:27)由0.968节点降为0.95后,从节点序号20开始,直到节点30(个别节点除外),电压幅值有较为明显的增加,其余节点的电压幅值未发生变化或变化不明显。
结论:对于降压变压器,降低变压器变比(大于0)调压后,电压幅值升高。
图5 降变压器变比前后电压幅值
3 结 语
本文采取三种主要调压方式(并电容器调压、改变发电机端电压调压和升降变压器变比调压),分别进行电压调整,仅得出定性结论,且由于功率损耗变化较小所以并未讨论,实际调压时需结合电压相角、功率损耗等满足调压要求。
使用Matpower进行潮流计算前,应检查计算要求是否与软件默认选项一致,若不符合,应事先修改设置再运行。
在潮流计算结果统计时,大量的数据无法直接复制到表格,因此可以利用Matlab编程语言强大的数值计算能力,通过编写简单的程序准确、高效地提取所需标准阵列的数据。
参考文献
[1]于永源,杨绮雯.电力系统分析(第三版)[M].北京:中国电力出版社,2007.
[2]刘笙.电气工程基础(下册)[M].北京:科学出版社,2008.
[3]何仰赞,温增银,汪馥瑛,等.电力系统分析[M].武汉:华中理工大学出版社,1996.
[4]孟祥萍,高燕.电力系统分析[M].北京:科学出版社,2004.
[5]刘天琪,邱晓燕.电力系统分析的计算机算法(第一版)[M].北京:中国电力出版社,2009.
[6]Carson W.Taylor.电力系统稳定[M].王伟胜,译.北京:中国电力出版社,2002.
[7]苏小林,阎晓霞.电力系统分析[M].中国电力出版社,2007.
[8]李红连,张维理,刘录东,等.潮流计算Matpower软件及其应用[J].重庆电力高等专科学校学报,2009,14(4):18-20.
[9]程浩忠.电力系统无功与电压稳定性[M].北京:中国电力出版社,2004.
[10]刘天琪,邱晓燕.电力系统分析理论[M].北京:科学出版社,2005.
[11]陈珩.电力系统稳态分析[M].北京:中国电力出版社,2007.
[12]韩祯祥.电力系统分析(第三版)[M].杭州:浙江大学出版社,2005.
[13]陈垦.直角坐标牛顿--拉夫逊潮流计算新解法[J].电力系统及其自动化学报, 1999(4):66-69.
[14]李霜.电力系统[M].重庆:重庆大学出版社,2006.
[15]李维波. Matlab在电气工程中的应用[M].北京:中国电力出版社,2009.
[16]何宁,王树臣,崔继仁.电力系统潮流计算的计算机算法[J].佳木斯大学学报 (自然科学版),1999,17(2):165-166.
[17]KESSEL P, GLAVITSCH H. Estimating the voltage stability of power system[J].IEEE Transactions on Power Delivery,1986,1 (3):346-354.
[18]Ajjarapu V. Computational techniques for voltage stability assessment and control[M].New York: Springer,2006.
