基于DSP Builder的FIR滤波器设计

张? 谢文博

摘 要：数字信号处理的稳定性、有效性和精确性使其应用范围越来越广。FPGA具有可根据自行需要而改变设计电路的功能，在数字电路领域不断发展，但它编程的语言繁琐而且不易理解。为此，采用DSP Builder进行FIR滤波器的设计，不仅可以自动转化为FPGA芯片能识别的语言，还可以进行模型化仿真。根据FIR滤波器的滤波原理，通过DSP Builder工具，设计一个20阶的低通滤波器，并进行了仿真。

关键词：DSP Builder；FIR滤波器；Matlab；FPGA

中图分类号：TN713 文献标识码：A 文章编号：2095-1302（2016）05-00-03

0 引 言

滤波器是用来抑制或滤除输入信号中的干扰或干扰成分，改变输入信号中各个频率分量的大小和相位，输出有用或达到预期指标的信号[1]。随着电子技术的不断发展，芯片集成度不断提高，数字滤波器不断取代模拟滤波器[2]。数字滤波器分为无限脉冲响应（IIR）和有限脉冲响应（FIR）两类，相比于IIR滤波器，FIR滤波器不存在递归运算，即不存在除零以外的其它极点，系统总是稳定的，也容易实现线性相位；虽然在实现过程中计算量较大，但设计方便，在通信、数字图像处理、雷达信号分析和谱分析等领域都有广泛的应用。

1 FIR滤波器

1.1 FIR滤波器原理

FIR滤波器指的是用有限冲

其中，M表示滤波器的阶数，h（i）表示系统的单位冲激响应，这由选择的滤波特性决定。一个理想的滤波器其单位冲激响应是一个无限长的序列，而FIR滤波器的阶数显然是有限的，这就要通过一定的附加函数逐步逼近理想的滤波特性。x（n-i）是通过i个延时后的数字输入信号。

1.2 FIR滤波器结构

FIR滤波器系统基本运算如图1所示。该结构图可以看成是一个分节的延时线，把每一节的输出加权累加，得到滤波器的输出[3]。由图可以看出，FIR滤波器可根据需要而加长或缩减延时线的长度和乘法器的系数来改变FIR的参数。FIR滤波器实际上是一个采用有限精度算法实现的时不变线性离散系统[3]。此结构是上述表达式（2）的直接反应，除此以外，还可以根据微机所提供的资源对系统结构进行改进，达到节约资源或节省运行时间的目的。

图1 FIR滤波器的基本结构

FIR滤波器一般是由乘法器、加法器、延时器构成，以进行数值计算和数据存储。由于处理时间和芯片资源空间相互制约，通过调整延时线长度和乘加次序来改变时间和空间之间的要求。当滤波器数据流向处理方式不同时，滤波器形成串行、并行、模拟卷积运算的分布式处理等结构。这里不展开说明，根据实际情况选取合适的滤波结构。总之，滤波器结构的选取不仅会影响滤波器自身的滤波性能，还会影响资源的合理利用。

1.3 FIR滤波器系数

在低通滤波器的设计过程中，要有理想的截止频率必须是无限长序列。对FIR滤波器来说，没有递归运算，只有有限阶抽头数，这就需要通过一定的设计方法，使误差达到最小值。把理想系统的单位冲激响应h（n）用一定的计算公式选择出有限长度的hd（n），以此hd（n）来逼近理想的h（n）。有限的抽头数就是FIR滤波器的系数，与滤波器的阶数对应。不同的逼近方法对滤波性能产生不同的影响。在设计系统的过程中要考虑通带，阻带，衰减程度，波纹等因素，避免系统达不到理想的设计要求。

根据不同FIR滤波器性能的要求，选取恰当的系数与滤波器阶数。一般有三种普遍的做法，分别为窗函数、等波纹最佳逼近、频率抽样。

（1）窗函数设计方法是将主要频率的值选出而舍弃一些对信号影响不大的值。当时域有限而频域无限时，就不会有良好的截止频率，这对信号贡献较大的频率成分不会有大的影响，截止频率附近的成分也可忽略不计；

（2）等波纹最佳逼近法处理比较粗糙的频率范围时经常使用，较低的阶数就能达到要求；

（3）频率抽样法是在频域范围内对信号进行数字处理，一般采用FFT的方法进行数据变换，其算法复杂。

2 设计流程及相关工具使用

2.1 DSP Builder的相关介绍

DSP Builder不是一个独立的软件，而是一个算法级的工具，作为一个子函数库存在于Matlab＼SimuLink中，同时得到Altera公司的授权，自动生成系统代码，完成硬件实现。随着数字信号处理技术的不断发展，FPGA应用的空间范围越来越广泛，但其实现目标所用的VHDL等硬件描述语言比较复杂。由Altera公司设计的数字信号处理工具DSP Builder简化了数字系统设计的流程，设计效率得到了提高。除此之外，其为数据类型的转化提供了一个很好的工具。

DSP Builder作为Matlab数值计算软件和QuartusII硬件设计软件之间的桥梁，一定程度上降低了设计的复杂程度，使设计更加简单且易于操作，避免了复杂的语言设计和逻辑验证过程。

2.2 FIR滤波器设计要求

在实际设计过程中，数字滤波器要根据其性能指标选取合适的逼近系数h（n），选取滤波阶数，确定滤波器的结构。设计要求为设计一个系统的抽样频率为Ft=50 MHz，通带截止频率为Fp=1 MHz，阻带截止频率为Fs=4 MHz，通带允许起伏1 dB，阻带最小衰减30 dB，滤波阶数为20阶的低通滤波器。由于窗函数设计的滤波器对频率要求比较精细，若此系统采用窗函数法，则需要很高的滤波阶数，因而这里采用通带频率比较粗略的等波纹设计法。

2.3 确定滤波器系数

滤波器系数的确定是滤波器设计最关键的一步，直接影响滤波器的实际性能。Matlab中的FDA提供了所需系数的设计工具。

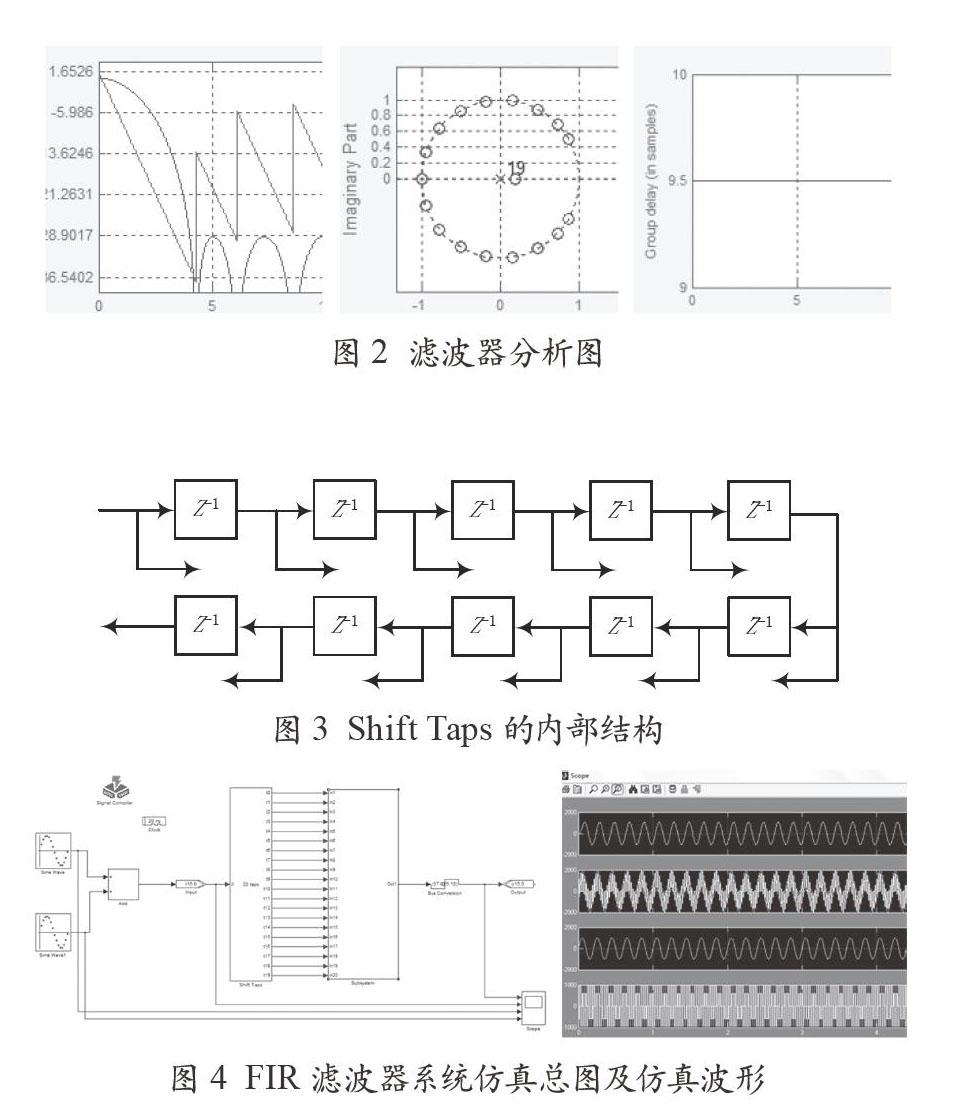
在这个过程中，FDA Tool算出的滤波器系数为有符号小数，需要处理能在FPGA中实现的有符号整数，这就要进行量化和归一化处理。量化的过程就是误差产生的过程，该过程会产生量化噪声，因此对量化后的滤波器进行性能分析是必须的。由滤波系数的特点可知，所得数据都需进行同等倍数处理，将其化成整数，尽量降低转化误差。得到处理后的滤波器系数依次为：-6 24 27 37 50 63 75 85 93 97 97 93 85 75 63 50 37 27 24 -6。这些系数直接决定了所占乘法器的位长。在求取滤波器系数的过程中，FDA Tool提供了极大的方便。作为Matlab中专门设计滤波器系数的工具，可以很直观地显示出FIR滤波器的幅频特性，零极点，群延时等参数，如图2所示。

图2 滤波器分析图

2.4 FIR滤波器模型的建立

利用DSP Builder工具设计FIR滤波器，在Matlab＼SimuLink中建立.MDL文件。通过.MDL文件转化为硬件能识别的VHDL语言，此软件仿真层的原理框图是构成FIR滤波器实际应用的基础。此过程也决定了滤波器的滤波结构即数据处理过程的顺序。Shift Taps内部结构如图3所示。FIR滤波器系统的仿真总图及仿真波形如图4所示。

图3 Shift Taps的内部结构

图4 FIR滤波器系统仿真总图及仿真波形

利用DSP Builder设计软件仿真的流程，并没有下载到FPGA中的文件。这只能说明设计逻辑的正确性，不能保证此系统的使用性。此时，必须通过一定的方式将其转化为硬件能够识别的.sof文件[2]。

2.5 FIR低通滤波器系统的硬件测试

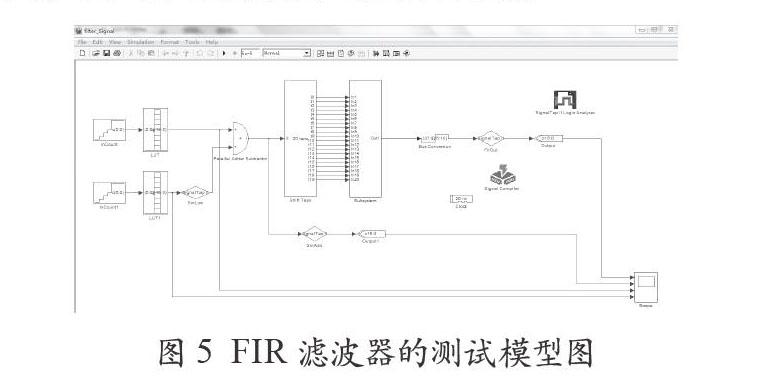
在仿真完成后，采用SignalTap II逻辑分析仪工具进行硬件测试的结果如图5所示，生成.sof文件下载到硬件中，前提是通过Signal Compiler编译后生成.qpf文件，使EDA工具QuartusII可编译。SignalTap II工具的应用缩短了测试时间，其将逻辑分析模块嵌入FPGA中，对待测节点的数据进行捕获就要通过逻辑分析模块。数据通过JTAG数据线进行数据传输。使用SignalTap II无需额外的逻辑分析设备，只需将一根JTAG接口的下载电缆连接到要调试的FPGA器件[4]即可。与ModelSim仿真相比较，该方法更直接的将设计用于硬件测试，并非只是对系统的数据运算进行检测。

图5 FIR滤波器的测试模型图

在测试过程中，用Signal Tap II分析块选取了输入的低频信号SinLow，不同频率的合成信号SinAdd，滤波输出的信号FirOut。硬件测试波形如图6所示，SinLow与FirOut检测所得的信号基本一致，他们都滤除了高频成分，滤波器输出的信号大致为390 kHz。由DDS原理所产生的低频正弦波信号的频率为390.625 kHz，产生的高频正弦波信号为6.25 MHz。这表明滤波器滤除了高频成分，达到了低通滤波器的基本功能。观察取样波形，输出波形FirOut与输入信号SinLow的波形大致一致，而在波峰与波谷处出现了失真。

图6 硬件测试波形

3 结 语

在此次设计过程中，充分展示了DSP Builder设计工具的优势，作为数字系统的设计工具，很好地搭建了一座Matlab与Quartus II共同设计系统的桥梁，同时也很好地转化SimuLink中建立的模型图，将其转化为Quartus II能识别的VHDL语言，避免了复杂的硬件语言描述[5]，大大缩短了系统的开发周期。此设计模式为FPGA在信号处理应用方面提供了很大的发展空间。

参考文献

[1]郑君里，应启衔，杨为理.信号与系统（下册）[M].北京：高等教育出版社，2011.

[2]高亚军.基于FPGA的数字信号处理[M].北京：电子工业出版社，2012.

[3]数字信号处理（第4版）[M].余祥宇，译.北京：电子工业出版社，2012.

[4]马建国，孟宪元.FPGA现代数字系统设计[M].北京：清华大学出版社，2010.

[5]邹兴宇，程树英.优化FIR数字滤波器的FPGA实现[J].现代电子技术，2011，34（6）：151-153.

[6]杨丽杰，崔葛瑾. 基于FPGA的FIR滤波器设计方法的研究[J].东华大学学报（自然科学版），2006，32 （6）：93-96，106.

[7]宋承文，魏选平，刘浩淼.基于FPGA的FIR滤波器设计与仿真[J].电子技术，2011（4）：49-51.