生产商Stackelberg下零售商提供通用服务的供应链博弈研究

鞠成杰 王磊

摘 要：针对由2个生产商和1个零售商组成的供应链，研究生产商作为领导者时，零售商采用加成定价法且提供通用服务对参与方定价和服务决策的影响。结果表明：随着服务敏感系数的逐渐增大，产品的批发价、零售价相应提高。当产品价格弹性增大时，零售商降低服务水平，而当产品之间替代性减弱时，零售商提高服务水平。提供通用服务虽然导致零售商利润先增大后减小，但供应链中每个参与方的利润都比不提供服务时大。

关键词：供应链；加成定价法；通用服务；斯坦克尔博格博弈

中图分类号：F273.7 文献标识码：A

Abstract： The influence of service cost of the retailer on the optimal price and the service decision are studied in a supply chain composed of two manufacturers each of whom makes a kind of product and a common retailer who adopts the strategy of markup pricing and provides the universal service. The results show that the wholesaling price and retailing price both increases with the service-related parameters increases. The service level is low when the sales of products are effected dramatically with the change of the price， but high about the two kinds of similar products. Although the profits of the retailer first increase and then decrease with the service from the retailer， the profits about everyone of the supply chain is more bigger than that without universal service.

Key words： supply chain； markup pricing； universal service； Stackelberg game

0 引 言

随着市场动态和竞争环境的变化，为在整个市场获得更多的利润，零售商必须采用更复杂的策略，而非简单的降低价格。服务作为一种非价格因素，逐渐成为影响消费者购买的重要因素。

有关于服务问题，王磊，刘圆圆，孙浩（2014）[1]研究了由2个生产商和1个共同零售商组成的供应链，研究生产商的服务补贴政策对参与方最优定价和服务决策及利润的影响；罗卫，张子刚，欧阳明德（2014）[2]研究了1个生产商和1个零售商在品牌投资、地方广告支出和广告费用共享规则上进行交易时纵向合作广告的效率；许明辉，于刚，张汉勤（2006）[3]在只含有1个生产商和1个零售商的供应链中，分别由不同方提供服务时，在MS、RS、NS情形下，对各参与方利润、价格制定策略的影响比较；Ganesh Iyer等（1998）[4]研究了零售商提供非价格因素，与不提供非价格因素下，生产商与零售商在整条供应链中如何协调，并给与了非价格因素衡量的模型；Xiaonan Han等（2014）[5]研究了1个生产商和2个零售商，生产商提供两种可以相互替代的产品并提供相关的服务，每个零售商只能订购两种中的一种，随着两种替代品的价格与服务水平的变化，对整个市场需求量的影响；Tiaojun Xiao等（2008）[6]研究了在2个生产商和1个零售商下，其中1个生产商生产新型产品，另1个生产商生产翻新产品，两种产品都有售后服务。零售商购买他们的商品可以自由定价，分析研究零售商不同服务水平的制定对参与方定价等策略的影响。

以上研究了服务对供应链中每个成员不同情形下的影响，本文研究零售商提供服务，生产商不提供服务。它是零售商采取的能为顾客提供更大价值的行为，能促进整个市场的产品需求量的行为，例如场内促销、产品摆放位置与产品宣传，实时配送和用户体验等无产品品牌区别化的通用服务。即本文零售商提供的服务是指通用服务，对生产商所有品牌产品统一适用的服务，服务不因产品的不同而不同。

如今现实生活中，正如陈婧（2015）[7]所述，有的零售商青睐于一种简洁且具有指示性的定价策略：加成定价法。戢守峰（2002）[8]也指出，加成定价法历史悠久，应用普遍，简单易行，大大简化了企业的定价程序，采用这种方法可以保证各行各业获得正常的利润率，从而保证生产经营的正常进行，对于买卖双方都显得公平。即本文研究供应链中零售商采取加成定价法。

生产商控制了生产的原料和技术，所以本文研究了生产商作为Stackelberg主导者时，考虑了由2个生产商和1个共同零售商组成的供应链，零售商采用加成比例法定价且同时提供通用服务销售产品。

1 基本模型

在本文研究的供应链中，有2个生产商生产不同的产品。2个生产商分别卖给1个共同零售商自己生产产品，且1个生产商只卖1种产品给零售商，零售商最终将产品在批发价基础上用固定加成比例法制定零售价来销售，并且提供无差异化服务，以增加顾客购买积极性。本文假定生产商与零售商为各自的经济独立实体，所有的活动发生在同一期间内，市场上每个零售商间距离太远以至于彼此之间不会构成竞争。然而，却可以让竞争集中在2个生产商上。以上是整个市场的重要大前提。假定顾客需求是受两个因素的影响：零售价和由零售商提供的通用服务。

1.1 需求函数

假定1 顾客对2个产品的需求度相当。产品的市场需求随着自己零售价的增加而减少，随着竞争者零售价的增加而增加。

假定2 一方零售价的减少会导致一部分顾客从另一方转入这方，而不是放弃购买产品。

假定3 服务的提供会使整个市场顾客需求增加。

正如S.CHAN CHOI（1991）[9]所述，本文的模型使用线性双寡头垄断市场需求函数来描述产品的需求函数，即：

QP，P，S=a-b+θP+θP+θS （1）

其中：a>0， b>0， θ>0， θ>0， b+θ>θ， i=1，2， j=3-i， a为市场规模；b为价格弹性，价格变动对自身的敏感系数；P为零售商销售产品i的价格；θ为价格竞争强度，2个产品价格变动的敏感系数，θ越大，产品间替代性越强；θ为服务对需求的促进强度；S为零售商提供服务的服务水平或服务量。

1.2 成本函数

假定4 所有的供应链成员会试图增大他们自己的利润，并且最终每个成员会以最佳需求量与成本结构来制定策略。

生产商利润受产品批发价、产品成本、产品市场需求量的影响，即：

∏M=w-cQP，P，S， i=1，2 （2）

为了描述零售商的利润函数，本文注意到零售商会有2个成本：产品成本和服务成本。产品成本大前提是零售商采用加成定价法，在加成比例一定的条件下，单位产品的利润视批发价的多少。服务成本包括提供给顾客的服务，例如：在服务部门员工的薪金，这些员工培训成本，或者从外界雇佣员工提供服务的成本等。正如Ganesh Iyer等（1998）[4]所述，这里又引出一个假设：

假定5 提供服务成本C的函数是关于服务水平严格递增的凸函数，也就是说零售商所投资的下一单位所获得的服务比所投资的上一单位获得的服务少。

这个缩减的服务效应可以用二次形式表示，即C=ηS/2，其中η为服务成本系数，与服务提供者相关。因此零售商的利润函数，即：

∏R=P-wQP，P，S-ηS/2， i=1，2 （3）

其中：P=1+tw，t为固定常数，P-w=tw是不考虑服务成本时，销售单位一方产品获得的利润，即为批发价的基础上乘以固定的比例。

现在以生产商作为整条供应链主导者，讨论有通用服务成本的零售商作为跟随者的情形。

2 零售商提供通用服务的决策

2.1 零售商的决策

生产商主导的Stackelberg博弈下，零售商对于2种产品的零售价P，采用加成定价法，关键是看零售商有关S的定价策略，需求出零售商利润有关S的一阶导数，并令其等于零，即：

=-Sη+twθ+twθ=0 （4）

零售商利润有关S的二阶导数为-η，可见提供服务时，零售商利润关于服务水平是个凸函数，故零售商利润有极大值点。由大前提及（4）式可得出零售商的反应函数如下：

P=1+tw （5）

S= （6）

命题1 S与θ成正比，即随着服务敏感系数的增大，零售商会相应提高服务水平。

命题2 S与w，t成正比，即随着批发价、加成比例的增大，零售商会相应提高服务水平。

2.2 生产商的决策

生产商利用零售商的反应函数决定最优的批发价，即将反应函数（5）式、（6）式联合带入生产商的利润函数（2）式中，再对其求一阶导数并令其等于零，即：

=a+1+twθ-1+twb+θ++-c+w-1+tb+θ+=0 （7）

此时生产商利润有关批发价的二阶导数为-21+tb+θ+2tθ/η，令其小于零，即0<θ<时，生产商利润才存在最大值。

解上述方程组得出生产商对应的最优批发价w，最优价格P，最优服务水平S，即：

w=- （8）

P=-1+t （9）

S= （10）

命题3 S与市场规模a成正比，即随着市场规模增大，零售商提供的服务水平越高。

3 零售商不提供通用服务

零售商不提供通用服务时，市场需求函数如下：

QP，P，s=a-b+θP+θP （11）

其中：a>0， b>0， θ>0， b+θ>θ， i=1，2， j=3-i

零售商成本只受产品成本的影响，即：

∏R=P-wQP，P （12）

且零售商采用加成定价法，最终得出相应生产商的最优批发价w，进而有零售商的最优价格P，即：

w= （13）

P=1+t （14）

4 数值分析

通过以上最优解，针对产品1、产品2进行数值分析，令a=100，a=120， c=3，c=4， η=4且已知加成比例为常数，可令t=0.2，且有0<θ<的大前提范围，其他系数大于零的条件恰当赋值分析。

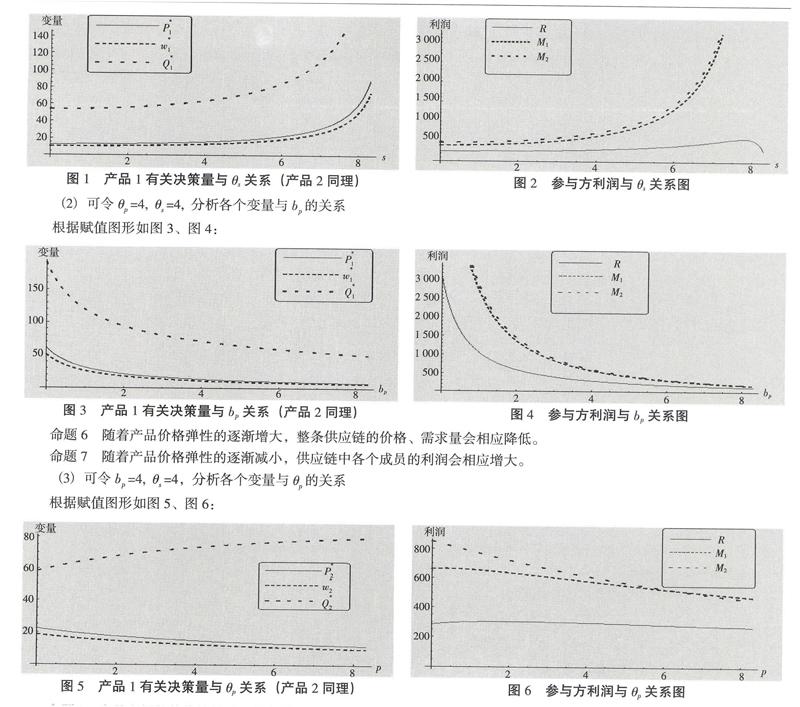
（1）可令b=4， θ=2， 分析各个变量与θ的关系

根据赋值图形如图1、图2。

命题4 随着服务敏感系数的逐渐增大，整条供应链的价格、需求量会相应提高。

命题5 随着服务敏感系数的逐渐增大，生产商及整条供应链的利润相应增加，而零售商的利润先增大后减小。

可见，对于零售商来说，零售商的利润有一个恰当的服务敏感分界值，使得零售商的利润最大，并不是服务水平越高越好。

（2）可令θ=4， θ=4， 分析各个变量与b的关系

根据赋值图形如图3、图4：

命题6 随着产品价格弹性的逐渐增大，整条供应链的价格、需求量会相应降低。

命题7 随着产品价格弹性的逐渐减小，供应链中各个成员的利润会相应增大。

（3）可令b=4， θ=4，分析各个变量与θ的关系

根据赋值图形如图5、图6：

命题8 产品之间的替代性越强，整条供应链的价格会相应减小，而市场需求量增大。

命题9 产品之间的替代性越弱，生产商及整条供应链的利润会增大，而零售商利润先增大后减小，但增大幅度不明显。可见，对整条供应链各个成员来说，应选择产品间替代性弱的产品为益。

（4）前面命题已经指出S与θ的关系，可令θ=4， 研究S与θ，b的关系

根据赋值图形如图7：

命题10 产品价格弹性越小、产品间替代性越弱，零售商会相应提高服务水平。

5 结束语

本文是在2个生产商和1个共同零售商的供应链中，零售商采用固定加成定价法且向消费者提供无差异化通用服务。由于生产商在制造链中占据垄断地位，他拥有零售商相关的成本信息，所以本文研究以生产商主导的Stackelberg博弈研究。本文发现，价格弹性越大的商品，零售商提供服务水平会相应降低，而产品间替代性越弱，零售商提供服务水平会相应提高。零售商提供通用服务时，生产商应该生产价格弹性小、产品间替代性弱的产品，例如努力生产创意性的产品，会使自己获得更大的利润；零售商应该选择价格弹性小，产品间替代性弱的产品，例如选择销售创意性的产品，会使自己获得更大的利润，虽然零售商应该相应提高服务水平，但是并不意味着提供服务水平越高越好。随着服务水平的提高零售商利润先增大后减小，所以零售商可以选择恰当的服务水平使得自己利润最大。总体来看，整条供应链各个成员的利润都比不提供服务时大，因此只要零售商提供通用服务，对整条供应链各个成员都有一定的益处。

参考文献：

[1] 王磊，刘圆圆，孙浩. 服务补贴与具有共同零售商的Stackelberg博弈研究[J]. 合肥工业大学学报（自然科学版），2014，4（4）：478-485.

[2] 罗卫，张子刚，欧阳明德. 基于一个博弈论方法的简单供应链合作广告模型[J]. 系统工程理论与实践，2014，2（2）：31-36.

[3] 许明辉，于刚，张汉勤. 具备提供服务的供应链博弈分析[J]. 管理科学学报，2006，4（2）：18-27.

[4] Ganesh Iyer. Coordination Channels Under Price and Nonprice Competiton[J]. Marketing Science， 1998（4）：338-355.

[5] Xiaonan Han， Xiaochen Sun， Yancong Zhou. The Equilibrium Decisions in a Two-Echelon Supply Chain under Price and Service Competition[J]. Sustainability， 2014（6）：4339-4354.

[6] Tiaojun Xiao， Danqin Yang. Price and service competition between new and remanufactured products in a two-echelon supply chain[J]. Production Economics， 2008（114）：187-200.

[7] 陈婧. 零售商主导的供应链中两种加成定价法的对比研究[D]. 北京：北京理工大学（硕士学位论文），2015.

[8] 戢守峰，邓德胜，赵浩兴. 现代市场营销学[M]. 北京：北京工业大学出版社，2002：211-212.

[9] S. Chan Choi. Price competition in a channel structure with a common retailer[J]. Marketing Science， 1991，10（4）：271-296.

[5] Hatefi S M， Jolai F. Robust and reliable forward reverse logistics network design under demand uncertainty and facility disruptions[J]. Applied Mathematical Modelling， 2014（38）：2630-2647.

[6] Das K， Chowdhury A H. Designing a reverse logistics network for optimal collection， recovery and quality-based product-mix planning[J]. General Information， 2012，135（1）：209-221.

[7] 代颖，马祖军，朱道立. 回收商管理库存下逆向物流多周期LRIP[J]. 工业工程与管理，2010（5）：1-6.

[8] 薛雷，王志平. 基于第三方物流的逆向物流优化模型[J]. 大连海事大学学报，2007（S2）：164-166，178.

[9] Winch J K， Madu C N， Kuei C. Metamodeling and Optimizing a Reverse Logistics System[J]. Internat. j. inform. management Sci， 2012（1）：41-58.

[10] 王亚楠，司玲玲，杜海艳. 基于双向反馈信息的逆向物流网络优化方法[J]. 计算机仿真，2012（10）：162-164，172.

[11] 陈达强，胡军，吴承健. 物流系统建模与仿真[M]. 杭州：浙江大学出版社，2008：149-151.

[12] Xianfeng L， Jianwei Q， Meilian L. Design and Simulation WEEE Reverse Logistics Network in Guangxi[C] // International Conference on Optoelectronics and Image Processing. IEEE， 2010：403-408.