一种高效的面向基2 FFT算法的SIMD并行存储结构
2016-05-31陈海燕
陈海燕,杨 超,刘 胜,刘 仲
(国防科学技术大学计算机学院,湖南长沙410073)
一种高效的面向基2 FFT算法的SIMD并行存储结构
陈海燕,杨超,刘胜,刘仲
(国防科学技术大学计算机学院,湖南长沙410073)
摘要:随着SIMD(Single Instruction Multiple Data stream)结构DSP(Digital Signal Processor)片上集成了越来越多的处理单元,并行访存的灵活性及带宽效率对实际运算性能的影响越来越大.本文详细分析了一般SIMD结构DSP中基2 FFT(Fast Fourier Transform)并行算法面临的访存问题,采用简单的部分地址异或逻辑完成SIMD并行访存地址转换,实现了FFT运算的无冲突SIMD并行访存;提出了几种带特殊混洗模式的向量访存指令,可完全消除SIMD结构下基2 FFT运算时需要的额外混洗指令操作.最后将其应用于某16路SIMD数字信号处理器YHFT-Matrix2中向量存储器VM的优化设计.测试结果表明,采用该SIMD并行存储结构优化的VM以增加18%的硬件开销实现了FFT运算全流水无冲突并行访存和100%并行访存带宽利用率;相比优化前的设计,不同点数FFT运算可获得1.32~2.66的加速比.
关键词:快速傅里叶变换;单指令多数据流;低位交叉;并行存储;访问冲突;数据混洗
1 引言
无线通信、图像匹配、视频解码等各类流媒体应用需求的不断增长对微处理器的运算能力提出了更高的要求,单指令多数据流(Single Instruction Multiple Data stream,SIMD)扩展结构因其硬件控制结构简单、能开发大量的数据级并行,可在相对较低的功耗下实现高数据吞吐率计算能力等特性,已成为各类通用或嵌入式微处理器的重要扩展,如Intel的SSE1/SSE2/SSE3[1]、ARM的ARMv6架构[2]、Michigan大学的AnySP[3]等.SIMD扩展能有效开发子字数据并行;在具有连续、对齐等规则向量访存模式的应用中具有很好的加速性能.但访存模式较复杂情况下,其性能并未随SIMD扩展可执行资源的增长而线性增加[4],其中额外的数据混洗置换操作造成的低SIMD访存带宽利用率是其中的一个重要原因.J.W.库利和T.W.图基提出的FFT[5]是无线通信等各类嵌入式应用的核心算法,具有很高的数据密集性、并行性;如何在SIMD结构DSP中实现高效的基于存储结构的FFT算法、获得高吞吐率的实际运算性能,设计一个支持连续数据流访问的无冲突、高带宽利用率的SIMD并行访存结构成为关键.
传统的FFT硬件加速器通常采用基于流水的单路径延时反馈结构[6]或基于存储结构[7].前一结构使用大量并行的蝶形运算单元实现多级蝶形运算的流水并行,针对特定点数、固定基FFT算法具有很高的数据吞吐率,但要耗费大量硬件资源,缺乏灵活性,不适合SIMD结构DSP;后一种结构针对特定一套蝶形运算单元,基于同址存储机制,能有效控制面积和功耗,但难以获得较高的FFT加速性能,但对其进行SIMD扩展和并行访存结构优化,SIMD结构DSP可望在有效的功耗预算下获得较高的FFT运算性能.
针对基于存储结构的FFT实现,人们对如何为蝶形运算提供连续的并行数据已进行了大量研究.文献[8,9]都使用了多个单端口RAM实现特定蝶形运算单元的无冲突并行访存;文献[10]基于同址存储机制实现了一种连续数据流混合基FFT无冲突访存,但地址转换使用了取模运算,逻辑过于复杂;文献[11]使用简单的地址异或逻辑就实现了基2 FFT算法的无冲突并行访存.这些存储结构都专注于一两个特定基蝶形运算单元,都未说明SIMD结构下如何实现无冲突地址转换以及多个蝶形运算单元之间的数据混洗.而对于SIMD结构研究中,支持SIMD宽度非对齐访问可加速H.264/AVC、FIR等算法[12],但不会提高FFT向量化访存效率.文献[13]通过设计质数个存储体的方式避免SIMD并行访存冲突,但地址转换逻辑复杂,且存在一定未映射的存储空间浪费.文献[14,15]针对FFT或特定应用算法定制专用混洗操作指令,以提高相应算法的计算性能,避免全交叉开关实现任意模式数据混洗造成的过高功耗和面积开销;但并行访存数据仍未直接用于SIMD运算单元的计算,需要进行两个向量寄存器间额外的混洗指令操作,使SIMD并行访存的数据带宽直接利用率只有50%;增加了代码量和计算周期,还要占用较多的向量寄存器资源.随着SIMD宽度和数据带宽的增大,不断增加的向量寄存器端口数和交叉开关使硬件面积急剧增长,造成后端物理设计难以实现等问题.
本文分析了一般多宽度SIMD结构DSP实现FFT算法时面临的并行访存冲突和数据跨步混洗问题,在文献[11]的基础上进一步提出了用于FFT向量化加速的SIMD并行存储结构,采用乒乓存储结构和地址异或逻辑相结合的方式实现了低开销、低延时的SIMD并行访存地址转换.同时提出了带特殊混洗模式的SIMD访存指令,并将其应用于某16路SIMD数字信号处理器YHFT-Matrix2的向量存储器VM的优化设计,不仅实现了SIMD结构中基2 FFT向量化运算的无冲突访存,而且完全消除了FFT运算所需的向量寄存器间的混洗指令操作,使得FFT运算的SIMD访存数据带宽利用率达到100%.
2 SIMD结构DSP中FFT向量化算法面临的问题
2.1SIMD并行存储结构
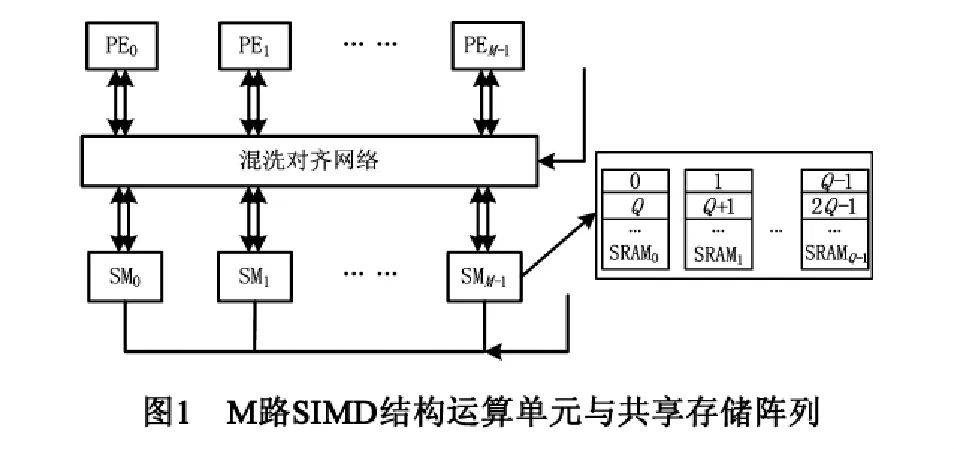
SIMD结构DSP集成了M路同构的运算单元(PE0~PEM-1)和多组向量寄存器,M路运算单元按SIMD方式操作.为了寻址计算简单快捷,一般选择M =2m,m为大于0的整数,并配置同样路数的共享存储阵列SM0~SMM-1,如图1所示.SM0~SMM-1按低位交叉全局统一编址以支持对应的PE运算访存.为充分开发PE的计算能力,共享存储阵列通常支持两条SIMD并行访存指令,能一拍为每个PE的运算提供两个操作数.由于容量相同的双端口存储体的面积和访问延迟比单端口存储体通常大30%以上,受限于芯片的面积和功耗,片上大容量存储器通常选择多个单端口静态随机存储体(SRAM)组织存储器;每个SM又按Q个单端口SRAM存储体低位交叉组织以提供并行访存带宽,一般Q = 2q,q为大于0的整数.这样能以较低的地址产生硬件开销为PE提供并行访存带宽.SIMD结构的存储阵列执行一条SIMD向量访存指令时,通常提供一组跨步为1的向量访存数据,为M个PE提供访存地址A起始的M个连续数据访存;而PE对存储阵列中数据的非连续或非对齐访问需要利用专门的指令通过混洗对齐网络在向量寄存器上实现数据对齐.
2.2面向FFT算法的SIMD访存模式
根据基2 FFT算法原理[5],长度为N(假设N = 2n,n为正整数)的序列X的FFT需要n级蝶形运算;每级蝶形运算又需要进行N/2次基本蝶形运算.在上述M 路SIMD结构DSP实现该算法时,M个PE一次可并行完成M个基本蝶形运算,那么每级蝶形运算中,每个PE要进行N/(2M)次基本蝶形运算;在不考虑系数情况下,需要N/(2M)次双操作数SIMD加载和N/(2M)次双操作数(即中间运算结果) SIMD存储操作.由于FFT运算中每个源操作数和中间结果只会在一个基本蝶形运算中使用一次,为提高存储器容量的使用效率,每级运算的中间结果采用“同址存储”,即基本蝶形运算的两数之和、两数之差分别存回第一、第二个操作数的原位置.因此SIMD结构中每个PE实现某级蝶形运算中的一个基本蝶形运算时,一个SM每次为对应PE提供的两个操作数的访存地址A1、A2存在如下关系:

其中n为N点基2频域抽取FFT运算需要的蝶形运算总级数,n = log2N; r为当前基本蝶形运算所处的级数,r =1,2,3,…,n.
将N点基2FFT算法在上述M路SIMD结构DSP实现时,一个PE进行某级蝶形运算需要的双操作数访存地址存在以下几种情况:
(1)当|A2-A1|>= M,即2n-r>=2m时,则在当前蝶形运算级数r<= n-m的蝶形运算中,M路SIMD结构中每个PE进行基本蝶形运算的两个操作数均来自同一SM;如果每个SM由Q = 2q个单端口存储体构成,根据两整数取模同余条件[16],可得到如下结论:
(a)当|A2-A1|能整除M* Q,即当r<= n-m-q时,A1、A2对2m + q取模同余,即:

此时,地址A1、A2访问同一个SM中的同一存储体,即M路SIMD结构中每个PE进行基本蝶形运算的两个操作数均来自同一SM中的同一个存储体;每次基本蝶形运算的并行访存都存在冲突.
(b)当n-m-q<r<= n-m时,每个PE进行基本蝶形运的两个操作数来自同一SM中的不同存储体,不存在访存冲突.通常,为了不浪费访存带宽,Q与所支持的并行访存指令数相等.
(c)当Q取大于1的奇数时,M* Q不是2的正整数幂,|A2-A1| modM* Q就不等于0,前(n-m)级蝶形运算的所有并行访存均不存在访问冲突.
因此,如果M路SIMD结构中每个SM按2q个SRAM存储体低位交叉组织存储器来提供双操作数访存,前(n-m-q)级中的基本蝶形运算存在大量的SIMD并行访存冲突;将显著降低SIMD并行访存带宽利用率,影响实际计算性能.如果按奇数个体组织存储体则消除了此冲突,但该方式地址计算逻辑需要实现访存地址整除求余的运算,其硬件实现复杂度远远大于Q等于2q时的移位逻辑.对于M路SIMD结构,两条SIMD访存指令就需要2M个这样的寻址单元;而且对于双访存操作,奇数个存储体还带来了冗余的访存带宽,这些都会造成较大的面积和延时开销.
(2)当|A2-A1|<M,即r>n-m时,在最后的m级蝶形运算中,由于每个PE进行基本蝶形运算的两个操作数的地址间距|A2-A1|小于M,每个PE进行一次基本蝶形运算的两个操作数将来自不同的SM,此时又需要对各PE运算使用的向量寄存器中的数据实现m种模式的混洗指令操作,这也会降低SIMD访存带宽的利用率.
因此,在基于上述单端口SRAM多体低位交叉方式实现并支持SIMD双访问的一般SIMD并行存储结构中,FFT并行运算将存在大量的向量访存冲突和额外的数据混洗指令操作,降低了SIMD访存数据带宽利用率,导致M路SIMD功能单元无法进行全流水连续的运算,将显著降低FFT的实际运算性能.根据上述分析,本文下面提出了一种支持FFT算法无冲突连续访存和特殊数据访存模式的低硬件开销的SIMD并行访存结构.
3 面向FFT算法加速的SIMD并行存储结构
3.1快速地址变换
文献[11]提出了一种针对序列长度和并行存储模块数均为2的正整数幂的基2 FFT算法的无冲突访存寻址方法,使用地址按位异或逻辑和地址旋转单元结合的访存地址产生器,能支持不同序列长度的FFT无冲突并行访存.本文在其基础上,针对上述M路SIMD并行存储结构设计了一种低硬件开销、适用于序列长度为2n的FFT运算无冲突访存的地址变换方法.
对于上述M路SIMD并行存储阵列,假设基2 FFT算法SIMD访存的数据字地址为n位,字粒度为w位字节,则SIMD访存数据的字节地址A可分为图2所示的几个域: SM的地址R3,为log2M = m位;每个SM中SRAM的体地址R2,为log2Q = q位;数据在某个SM中SRAM字节地址,由R1、R4构成.

对于序列长度N =2n的频域抽取基2 FFT运算,在前r级(r =1,2,…,n-m)的蝶形运算中,M路SIMD结构中每个PE进行基本蝶形运算的两个操作数均来自同一SM;只需对SM中的SRAM体地址R2进行转换,根据文献[11],可得到以下地址转换方法:
(1)将地址A[n + w-1: w + m]从低到高位按q位分组,构成一组向量F0,F1,…,Fp-1,将最后不能凑成q位的高e位看做向量L,其中p = (n-m) /q向下取整,e = (n-m) mod q,若e =0,则无向量L.
(2)若e! =0,则设置q位向量G,将(n-m)位地址的低(q-gcd(q,e) )位作为G的低位,gcd为求最大公约数运算;高位由0补齐;再将向量G向左循环移动g = (n-m-q) mod q位,得到向量O.
(3)如果e! =0,将所有向量Fi(其中i =0,1,…,p -1)和向量O、向量L按位异或;如果e = 0,则只将所有向量Fi按位异或,即可生成新的R2地址.
根据上面的结论,如果e =0,则无需产生向量O和L的逻辑,即无需地址旋转单元,地址转换逻辑只增加了p个q位向量的按位异或逻辑.对于支持双访问的SIMD并行存储结构,单个SM中满足双访问带宽的SRAM体至少为Q = 2q= 2,即q = 1,新的R2地址= ^A [n + w-1: w + m],这里“^”表示对向量进行按位异或的逻辑运算符.
3.2支持数据混洗的SIMD并行访存
频域抽取基2 FFT运算的最后m级蝶形运算中,由于每个PE进行基本蝶形运算的两个操作数的地址跨步|A2-A1 |小于M,一次基本蝶形运算的两个操作数将来自不同的SM,需要实现log2M = m种PE间数据混洗和对齐.如果用SIMD并行访存指令实现这几类数据混洗模式访问,就可以消除额外的混洗指令操作,减少向量寄存器访问端口的压力,提高SIMD访存的效率,并减少FFT并行运算的代码密度.
图3示例了SIMD宽度M =16时,使用两条并行的特殊SIMD访存指令VLS0/VLS1的混洗访存,实现了基2 FFT中4级蝶形运算需要的SIMD并行访问数据跨步为8、4、2、1共四种混洗模式.通过在正常的SIMD并行访存流水线中增加支持这四种模式数据交换与对齐单元即可实现.

4 应用与测评
4.1YHFT-Matrix2的总体结构
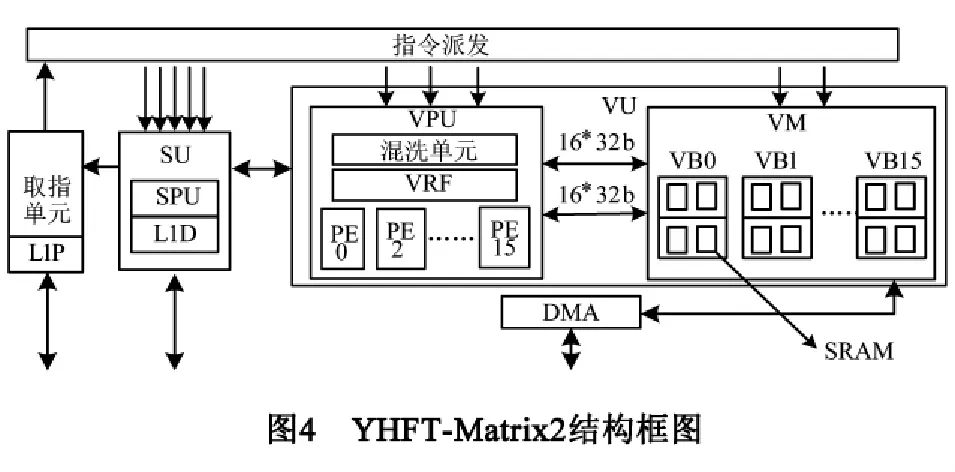
本文用上述方法对一款自主研发的32位数字信号处理器YHFT-Matrix2的向量存储器VM进行设计优化和测评.YHFT-Matrix2采用VLIW + SIMD技术和标量单元(SU)、向量单元(VU)并行结构,以充分开发指令级和数据级并行.标、向量单元共享取指单元和指令派发部件,实现标量、向量数据的并行处理,其结构框图如图4.其向量单元VU包含16路SIMD结构的向量运算单元VPU和程序员可见的片上大容量向量存储器VM.VPU内集成16个同构的PE和32深度的向量寄存器文件(VRF),每个PE有1个乘法、1个ALU和1个支持混洗模式可编程的全交叉结构混洗单元[17],可并行执行三条SIMD向量运算指令.VM为16个PE运算提供向量数据访存,容量为1MB,由16个向量存储体(VB0~VB15)按地址低位交叉组织,且采用支持SIMD非对齐并行访存结构[18].VM可同时支持两条SIMD访存指令和DMA读/写三请求并行访问,一拍可为VPU中的每个PE提供两个32位字操作数访存.为支持多请求并行访问,VM采用了高、低位地址统一编址,即按低位地址方式组织16个VB,每个VB采用了4组单端口SRAM,将4* 16 =64个SRAM按高、低位地址交叉方式组织,低位交叉满足SIMD并行访存带宽需求;而按地址最高位交叉构成的乒乓存储结构又可减少SIMD访存和DMA读/写并行访问的冲突,隐藏运算数据传输延时.
4.2对YHFT-Matrix2的并行访存优化
(1) SIMD访存的地址变换
VM地址空间为1MB,其字节地址为A[19: 0],A[19]寻址每个VB内按高位地址组织的上或下一半地址空间,和A[18: 7]一起构成单个VB中的每个SRAM存储体内的字地址; A[6]用来寻址每个VB内上或下半地址空间中的某个SRAM存储体,A[5: 2]表示16个VB的地址索引.由于VB中上或下地址空间分别由2 个SRAM体按低位交叉组织;根据上文,q = 1,e = 0,只需要对寻址的上或下地址空间的两个SRAM的体地址A[6]进行转换得到A'[6],即可满足向量访存指令无冲突SIMD并行访存的需求,即:

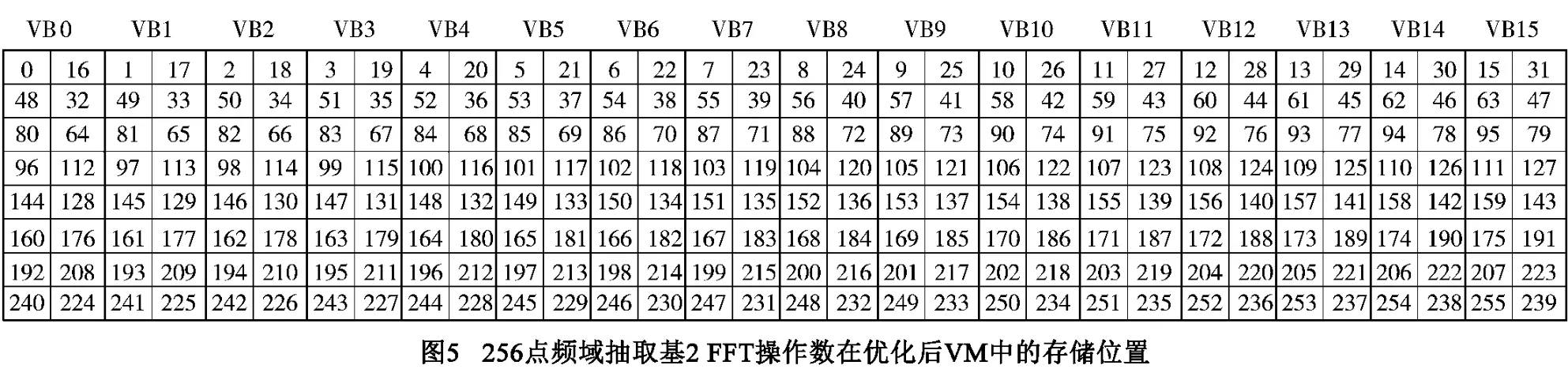
以256点为例,假设其原存储字地址为VM的255 ~0;进行地址变换优化后,根据式(3),256个数据将如图5所示地址存储.因此在基2 FFT的前4级蝶形运算中,每个PE基本蝶形运算的双操作数都可实现无冲突并行访存.同时对于基4算法,所需操作数也可以分两次无冲突访存实现.
(2)支持FFT算法混洗的SIMD并行访存
对于16路SIMD结构,在频域基2 FFT蝶形运算的最后4级或者基4蝶形运算的最后两级需要进行SIMD双访存数据混洗操作.VM需要设计如图3所示的4种带特殊混洗模式的向量访存指令,在VM原来向量访存流水线中增加了访存前、后四种模式的数据混洗对齐逻辑,如图6所示,通过SIMD并行访存指令,直接为每个PE提供基本蝶形运算所需的两个操作数.

4.3性能分析
(1)面积代价
对VM进行上述优化,用部分地址位异或逻辑改写地址A[6],增加访存前、后混洗单元,然后基于某厂家65nm工艺和1.3ns的时钟周期对优化后的VM进行逻辑综合,在相同综合约束下,优化前后的VM均满足时序要求.优化前后的综合面积如表1所示.结果表明,面向FFT的并行访存优化结构比原来VM的访存控制逻辑的面积增加18%,但由于该方法不需要可编程混洗单元,VM与混洗单元控制逻辑的面积和减少了32%.
(2)单精度浮点基2 FFT的运算性能
基于YHFT-Matrix2指令集体系结构和软件流水编程技术,编写了128~4096点浮点单精度FFT汇编测试程序,对采用上述SIMD并行访存优化设计前后的VM进行性能测试,得到表2所示测试结果.
从表2中可以看出,采用简单的地址变换后完全消除了基2 FFT SIMD并行访存冲突引起的访存停顿;支持带数据混洗SIMD访存操作,则消除了SIMD结构中FFT蝶形运算需要的额外混洗指令,减少了软件流水的最小迭代间隔,使实际的SIMD向量访存带宽利用率达到100%.使用优化后的VM,YHFT-Matrix2获得了1.32到2.66的加速比,特别是点数大于512点后,由于软件循环流水性能的提高,取到了更好的加速效果.

表1 YHF-Matrix2 VM优化前后面积对比(均不含存储体面积)
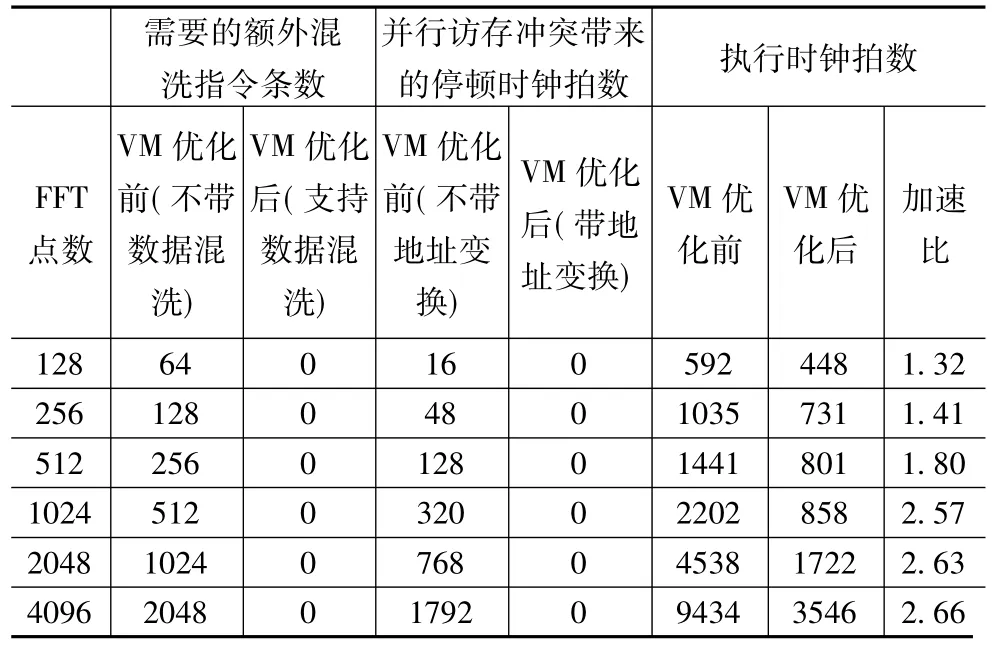
表2 VM优化前后浮点单精度FFT性能比较
5 结论
本文针对SIMD结构数字信号处理器中基2 FFT算法的访存模式存在的问题,提出了一种支持FFT算法无冲突并行访存和数据混洗的SIMD并行存储结构,能以较低的硬件开销实现FFT算法无冲突SIMD方式并行访存,消除了SIMD结构中向量寄存器间的混洗操作,使SIMD访存带宽利用率达到100%,有效提高了SIMD结构DSP的FFT运算性能,该方法应用于基4 FFT算法同样有效.
参考文献
[1]Intel Corporation.Intel 64 and IA-32 Architectures Software De-veloper Manuals,Volume1: Basic Architecture[OL].http: / / www.intel.com/products/processor/manuals,2015-01-05.
[2]ARM Corporation.The Architecture for the Digital World [OL].http: / /www.arm.com /zh/products/processors/ technologies/dsp-simd.php,2015-01-05.
[3]Woh M,Seo S,Mahlke S,et al.AnySP: anytime anywhere anyway signal processing[A].Proceedings of the 36th Annual International Symposium on Computer Architecture [C].Austin,Texas,USA: ACM,2009.128-139.
[4]Deepu Talla,Lizy Kurian John,Doug Burger.Bottlenecks in multimedia processing with SIMD style extensions and architectural enhancements[J].IEEE Transactions on Computers,2003,52(8) : 1015-1030.
[5]James W Cooley,John W Tukey.An algorithm for the machine calculation of complex Fourier series[J].Mathematics of Computation,1965,19(90) : 297-301.
[6]Yun-Nan Chang,Keshal K Parhi.An efficient pipelined FFT architecture[J].IEEE Transactions on Circuits and Systems-II: Analog and Digital Signal Processing,2003,50 (6) : 322-325.
[7]B M Baas.A low-power,high-performance,1024-point FFT processor[J].IEEE Journal of Solid-State Circuits,1999,34(3) : 380-387.
[8]Stephen Richardson,Ofer Shacham,et al.An area-efficient minimum-time FFT schedule using single-ported memory [A].Proceedings of 2013 IFIP/IEEE 21st International Conference on VLSI-SoC[C].Istanbul,Turkey: IEEE,2013.39-44.
[9]Ji-yang Yu,Yang Li.An efficient conflict-free parallel memory access scheme for dual-butterfly constant geometry radix-2 FFT processor[A].ICSP2008 Proceedings [C].Beijing,China: IEEE,2008.458-461.
[10]Chen-Fong Hsiao,Yuan Chen,Chen-Yi Lee.A Generalized mixed-radix algorithm for memory-based FFT processors[J].IEEE Transactions on Circuits and Systems-II: Express Briefs,2010,57(1) : 26-30.
[11]Jarmo H Takala,Tuomas S Jawinen,Harri T Sorokin.Conflict-free parallel memory access scheme for FFT processors[A].ISCAS ' 03[C].Thailand: IEEE,2003.IV524-527.
[12]Alvarez M,Salami E,Ramirez A,et al.Performance impact of unaligned memory operations in SIMD extensions for video codec applications[A].IEEE International Symposium on Performance Analysis of Systems&Software [C].California,USA: IEEE,2007.62-71.
[13]Hoseok Chang,Junho Cho,Wonyong Sung.Performance evaluation of a SIMD architecture with a multi-bank vector memory unit[A].2006 IEEE Workshop on Signal Processing Systems Design and Implementation (SIPS' 06)[C].Banff,Alta: IEEE,2006.71-76.
[14]Kai Zhang,Shuming Chen,Sheng Liu,et al.Accelerating the data shuffle operations for FFT algorithms on SIMD DSPs optimizing data permutations for SIMD devices[A].Proceedings of International Conference on ASIC (ASICON 2011)[C].Xiamen,China: IEEE,2011.683-686.
[15]Praveen Raghavan,Satyakiran Munaga,et al.A customized cross-bar for data-shuffling in domain specific SIMD processors[J].Lecture Notes in Computer Science,2007,4415: 57-68.
[16]张彦仲,沈乃汉.快速傅里叶变换及沃尔什变换[M].北京:航空工业出版社,1989.97-98.
[17]万江华,刘胜,等.具有高效混洗模式存储器的可编程混洗单元[J].国防科技大学学报,2011,33(6) :31-35.Wan Jianghua,Liu Sheng,et al.A programmable shuffle unit with the efficient shuffle pattern memory[J].Journal of National University of Defense Technology,2011,33 (6) : 31-35.(in Chinese)
[18]陈海燕,刘胜,刘仲,陈书明.面向SDR应用的向量访存控制器[J].国防科技大学学报,2012,34(3) : 98-102.Chen Haiyan,Liu Sheng,Liu Zhong,Chen Shuming.The design and optimization of the vector memory applying for SDR[J].Journal of National University of Defense Technology,2012,34(3) : 98-102.(in Chinese)

陈海燕(通信作者)女,1967年生,四川南充人.1989年、1992年分别获得国防科技大学工学学士和硕士学位.现为国防科技大学计算机学院研究员、硕士生导师.研究方向为微处理器体系结构、VLSI设计.
E-mail: hychen608@163.com

杨超男,1990年生于河南南阳.2013年毕业于国防科技大学计算机学院网络工程专业,现为国防科技大学计算机学院硕士研究生,研究方向为微处理器设计.
E-mail: 896331663@ qq.com
刘胜男,1984年生于河南南阳,现为国防科学技术大学计算机学院助理研究员,研究方向为高性能微处理器设计.
E-mail: liusheng83@ nudt.edu.cn
刘仲男,1971年生于湖南邵东.2005年获得国防科学技术大学计算机科学与技术专业博士学位,现为国防科学技术大学计算机学院研究员,主要从事芯片验证与性能评测、嵌入式应用与算法优化等方面的研究工作.
E-mail: zhongliu@ nudt.edu.cn
An Efficient SIMD Parallel Memory Structure for Radix-2 FFT Computation
CHEN Hai-yan,YANG Chao,LIU Sheng,LIU Zhong
(College of Computer,National University of Defense Technology,Changsha,Hunan 410073,China)
Abstract:As more and more execution units are integrated in the digital signal processor(DSP) with single instruction multiple data stream(SIMD) extension,the flexibility and bandwidth efficiency of parallel memory access have significant effects on its whole practical performance.Based on detailed analysis of the memory access problems for radix-2 fast Fourier transform (FFT) algorithm in general SIMD DSP,this paper used parts of the address bit XOR logic to realize memory access address translation,and achieved conflict-free parallel SIMD memory accesses for FFT computation.Then several memory access instructions with special shuffle modes were brought forward,which could completely eliminate extra shuffling instruction operations of radix-2 FFT algorithm in the SIMD architecture.Finally,the vector memory(VM) in 16-way SIMD DSP YHFT-Matrix2 was optimized by above methods.The test results show that the optimized VM can realize fully pipelined conflict-free memory accesses and 100% parallel memory access bandwidth utilization with increase of 18% area overheads.Compared with the design before optimization,the performance of different points radix-2 FFT can achieve speedup ranging from 1.32 to 2.66.
Key words:FFT; SIMD; low-order interleave; parallel memory; access conflict; data shuffle
作者简介
基金项目:国家自然科学基金(No.61472432)
收稿日期:2015-03-30;修回日期: 2015-05-28;责任编辑:覃怀银
DOI:电子学报URL: http: / /www.ejournal.org.cn10.3969/j.issn.0372-2112.2016.02.001
中图分类号:TP303
文献标识码:A
文章编号:0372-2112 (2016) 02-0241-06
