改进的粒子群算法及遗传算法在车间作业调度中应用的比较研究

摘 要：借鉴遗传算法及粒子群优化算法的思想，提出了一种改进的粒子群算法，并将其应用于车间作业调度问题。根据车间作业调度的目标函数建立起算法数学模型，采用改进的粒子群算法对车间作业调度进行优化，得到目标的全局最优解。仿真示例说明改进的粒子群算法优化车间作业调度的最小化加工时间目标比遗传算法明显更有效。

关键词：车间作业调度；粒子群算法；改进的粒子群算法；遗传算法；交叉；变异

0 引言

Job Shop调度问题（Job- shop scheduling problem，简称JSSP）研究具有重要的理论意义和工程价值，是目前研究最广泛的一类典型调度问题。粒子群优化（Particle Swarm Optimizer，简称PSO）算法是一种基于迭代的群智能演化优化工具，最早是由Kennedy J.和 Eberhart R.于1995年提出的，目前在函数优化、神经网络训练及模糊系统控制等领域得到较为广泛的应用[1]。与遗传算法比较，PSO的优势在于没有许多参数需要调整[2]，简单容易实现。本文在PSOA的基础上提出了一种改进的粒子群算法（Improve Particle Swarm Optimizer Algorithm，简称IPSOA），并将其应用到JSSP离散问题的优化中。

1 车间作业调度问题（Job-Shop Scheduling Problem，简称JSSP）

1.1 JSSP的描述

JSSP是组合优化问题中最困难的一类，调度目标是找到使用这些共同资源的一种排序，使生产约束被满足，同时使生产成本最低。JSSP是在m台不同机器上加工有特定加工工序和加工时间的n个工件。调度的目标就是确定各台机器上工件的加工顺序和每个工件在各台机器上的起始加工时间，使加工完所有工件所需的时间最少。

1.2 JSSP的数学模型

典型的JSSP问题有多种描述形式，通常采用Adams[3]提出的数学模型。是工件的工序集合，M表示机器集合，A是工序的先后顺序有序对集合，Em表示在机器m上加工的工序对集合，Pi表示第i道工序的加工时间，ti表示第i道工序的开始加工时间。JSSP可以表示为：

设工件j经过m道工序操作完成，且须按照给定的工序序列Oij（i=1，2，m，j=1，2，…，n）加工，即j工件的第i道工序在机器Oij上加工；

Tij（i=1，2，…，m，j=1，2，…，n）表示工件j的第i道工序的固定加工时间；C（k，j）表示工件j在机器k上的加工结束时间；Pij=find（Oj=i）为在工序矩阵Oij中，工件j在机器i上的工序。

n×m车间作业调度问题的完工时间表示如下：

即makespan为：

JSSP中优化的一个目标是找到一个可行调度方案，使得makespan最小。

2 算法

2.1 遗传算法（Genetic Algorithm，GA）实现的基本方法[4]

采用遗传算法来设计问题的求解方法，针对Job -Shop实际生产情况，具体设计环节如下：

（1）编码方案

编码方案采用整数编码，5×5车间作业调度问题具体编码如图1所示。

评价函数）

适应度函数是评价个体位串的适应性，本文根据JSSP问题的调度目标采用makespan作为算法的适应度函数。

（3）遗传算子

为了保证良好基因遗传给下一代，选择是从当前群体中选择适应度值较优的个体来生成交配池，最基本的选择方法是适应度值比例选择。交叉操作是进化算法中遗传算法具备的原始性的独有特征，通常采用的遗传算子包括一点、两点和多点等交叉形式。变异可以确保群体的多样性。

（4）初始化

初始化根据工件和工序数随机产生初始种群，以这些染色体为初始点进行迭代。种群规模可以随具体计算情况变化。

（5）终止循环的条件

采用最大代数的方法或算法的种群适应度平均值等于最优的运算结果则停止。

2.2 改进的粒子群算法

PSO算法是一种基于迭代的群智能演化优化工具，在优化过程中系统首先初始化为一组随机解，然后通过迭代在解空間搜寻到最优值。目前在函数优化、神经网络训练及模糊系统控制等领域应用较为广泛。本文提出了一种改进的粒子群算法（Improve Particle Swarm Optimization，简称 IPSO），该算法是在PSO算法中采用GA算法的交叉和变异操作，并将其应用于JSSP离散问题的优化。因PSO算法只适合解决连续问题的优化，所以用PSO算法来优化JSSP的关键是设计一种适合离散优化问题的有效机制。本文根据JSSP的特点提出了IPSO算法，具体设计如下：

（1）交叉和变异操作

交叉操作可分为：一段、二段、三段和四段交叉。一段交叉首先是在第一个父代中随机选取两个交叉点，然后把二交叉点间的工件序列复制到子代，最后在子代的其他位置依次用第二个父代的因子来代替。

Nearchou Ac在[5]中阐述了六种变异操作，对于不同规模的JSSP，最佳的变异操作方法是移动变异操作，该操作的工作原理是先随机选取一个移动点和一个插入点，然后对工件系列进行移动。

（2）最小化加工时间的JSSP改进粒子群算法的迭代模式

假设在一个由m个粒子组成的D维搜索空间中，其中表示第i个粒子在D维搜索空间中的位置。是第i个粒子的飞行速度，是迄今为止第i个粒子搜索到的最佳位置，是迄今为止整个粒子群搜索到的最佳位置[6]。IPSO的递推方程如下：

在（2-1）、（2-2）、（2-3）和（2-4）中，k为迭代代数，为粒子i在第k次迭代时飞行速度矢量的第d维分量；是粒子i在第k次迭代时位置矢量的第d维分量；是粒子i个体最优位置的第d维分量；为群体最优位置的第d维分量，显然，和都是符号或者自然数；是交叉算子符号，代表两个粒子或者速度进行交叉操作；，分别表示变异随机选择的速度和粒子，然后覆盖原来相对应的速度和粒子，rN表示总共需要变异的速度与粒子总数。

（3）IPSO算法的步骤

步骤l：初始化迭代代数k=0，迭代终止代数Maxgen，产生规模为psize的初始种群，计算种群中各粒子的适应值，从种群中选出第一代中的最优粒子PgBest；

步骤2：用公式（2-1）得到2×psize个粒子，计算其适应值，从中选出适应值较小的psize个粒子作为速度，再随机选择rN个速度用公式（2-2）进行变异，然后覆盖原来对应的速度。同理，利用公式（2-3）和（2-4）产生下一代粒子。判断，若新种群中各粒子适应值低于个体历史最低适应值，用新的最低粒子代替历史适应值最低粒子个体PiBest，同样判断新种群中的粒子适应值若低于全局最优值，用现在的全局最优粒子代替粒子PgBest；若k=Maxgen，转至步骤3，否则令k=k+1，转至步骤2。

3 IPSO和GA优化JSSP的仿真结果

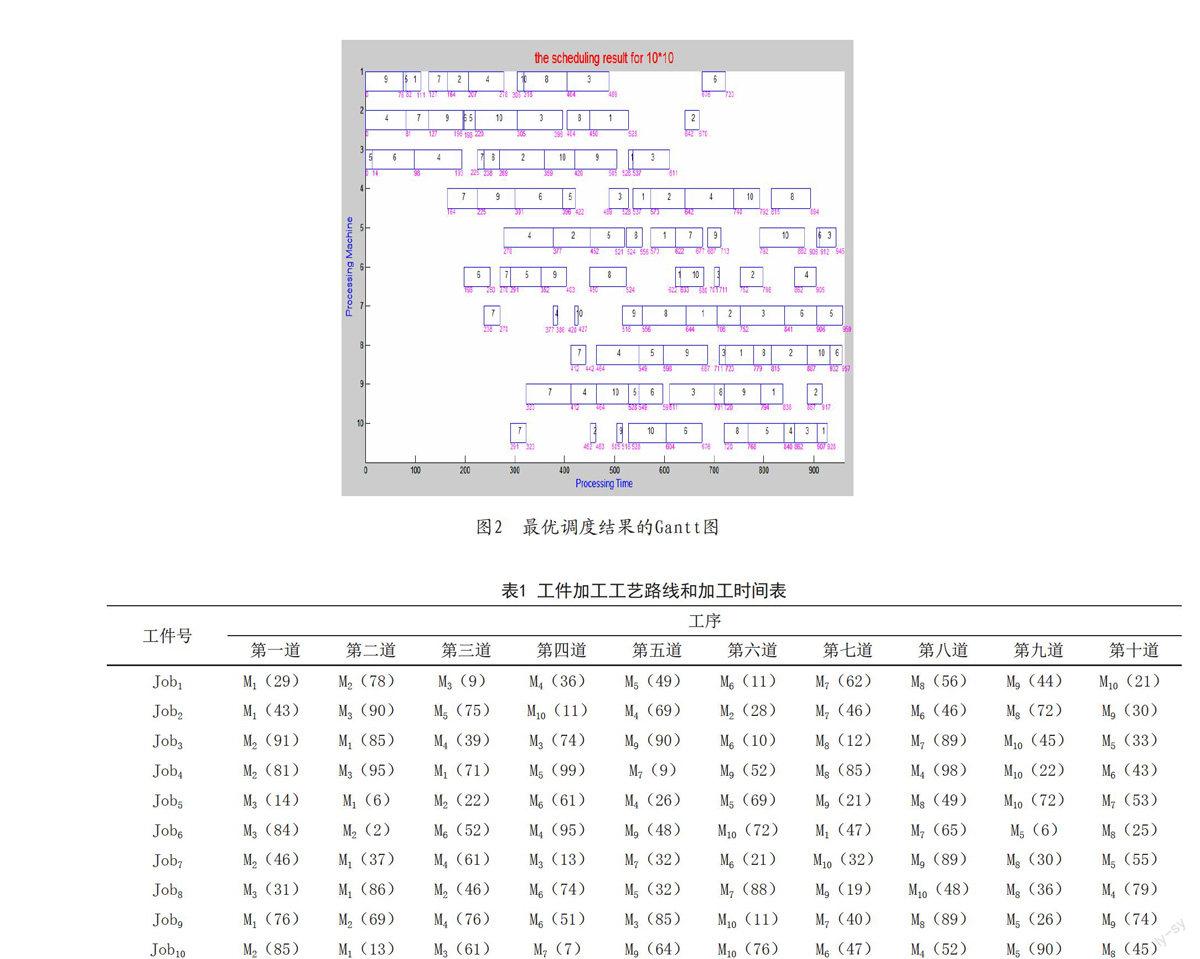
对10×10的车间作业调度问题采用遗传算法和改进的粒子群算法进行调度，10个工件的加工工艺路线和加工时间如表1所示。

图2是10×10 JSSP最优调度结果的甘特（Gantt）图。

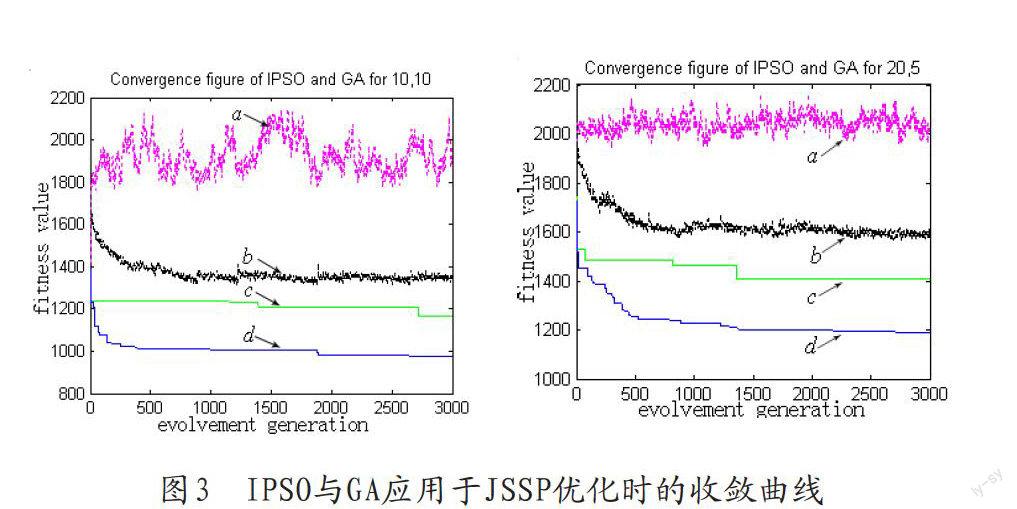
经过多次反复调试，在取进化代数为3 000、群体规模为30的情况下，采用IPSO算法和GA算法优化10×10 和20×5的JSSP典型例子，搜索最优解过程的收敛曲线比较图如图3所示。

图3中a线和c线分别表示GA算法优化JSSP典型例子时平均值和最优值的收敛速度，b线和d线分别表示IPSO算法优化JSSP典型例子时平均值和最优值的收敛速度。收敛曲线图的横坐标表示进化代数，纵坐标表示适应度。

4 结语

IPSO算法是基于PSO算法的思想，它们迭代方程不同，但信息来源相似，有用的信息都是主要来自个体历史最优粒子和全局最优粒子。IPSO算法相比PSO算法迭代方程添加了类似于GA的交叉和变异操作，即增加了粒子种群的多样性。在IPSO算法与GA算法中种群都是随机产生的，种群中的粒子是通过适应值进行评估的。GA更新种群是随机选择的染色体进行交叉和变异操作，基本PSO算法的粒子更新是基于权重的合并，IPSO算法采用了类似于GA中的交叉和变异操作，通过PiBest和PgBest信息共享來进行种群更新的。IPSO算法与GA相比，更易于搜索到全局最优值。仿真算例说明IPSO算法用于优化JSSP的最小Makespan目标相比GA更为有效。

参考文献

[1]潘全科，孙志峻，朱俭英.基于遗传算法在车间作业高度优化[J].信息与控制，2003，31（3）：216-218.

[2]Nearchou AC.The effect of various operators on the genetic search for large scheduling problems[J].International journal of production economics，2004，（88）：191-203.

[3]陈群贤.近似粒子群算法在Flow-shop调度中的应用.上海电机学院学报，2006，9（2）：16-18.