统计思想在生活中的应用

梅磊

统计学是研究如何收集、整理、分析数据的学科，它可以为人们制订决策提供依据. 而统计思想就是用样本估计总体，即通常不直接去研究总体，而是通过从总体中抽出一个样本，根据样本的情况去估计总体的相应情况. 它包含两类问题：一类是如何从总体中抽出样本；另一类是如何对样本进行整理、分析，从而对总体情况作出估计. 常用的方法是用样本的频率分布估计总体的分布，或者用样本的某个数字特征（如平均数、方差等）去估计总体的相应数字特征. 本文通过几个具体例题来介绍统计思想在生活中的应用.

学生视力调查

例1 为了了解某地区的中小学生视力情况，拟从该地区的中小学生中抽取部分学生进行调查. 事先已了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异，而男女生视力情况差异不大. 在下面的抽样方法中，最合理的抽样方法是（ ）

A. 简单随机抽样 B. 按性别分层抽样

C. 按学段分层抽样 D. 系统抽样

分析 根据三种抽样方法的特点判断.

解 因该地区小学、初中、高中三个学段学生的视力情况有较大差异，而男女生视力情况差异不大，故最合理的抽样方法是按学段分层抽样.

答案 C

点拨 抽样方法是统计学的基础，熟悉三种抽样方法的特点是解决此类问题的关键.

产品质量抽查

例2 从某企业生产的某种产品中抽取100件，测量这些产品的一项质量指标值，由测量数据得到如下频数分布表：

（1）作出这些数据的频率分布直方图；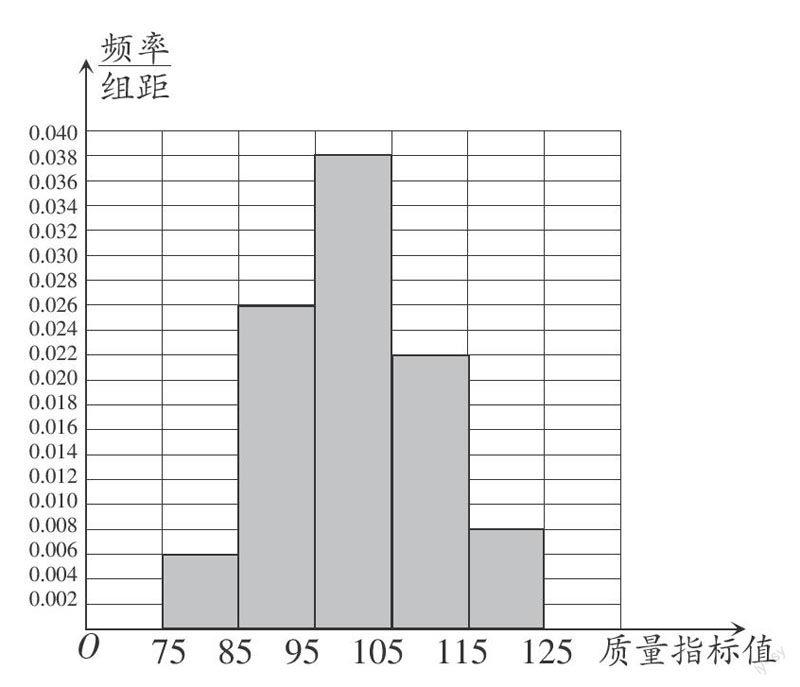

（2）估计这种产品质量指标值的平均数及方差（同一组中的数据用该组区间的中点值作代表）；

（3）根据以上测量数据，能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定？

分析 频率分布直方图的绘制并不复杂，关键是理解频率分布直方图的有关知识. 计算平均数和方差可直接利用公式，但要注意计算的准确性. 由样本计算质量指标值不低于95的频率，即可判断产品是否符合相关规定.

解 （1）频率分布直方图如图：

（2）由平均数与方差的计算公式得，质量指标值的样本平均数为，质量指标值的样本方差为，故这种产品质量指标值的平均数的估计值为100，方差的估计值为104.

（3）质量指标值不低于的产品所占比例的估计值为，

由于该估计值小于，故该企业生产的这种产品不符合规定.

点拨 在频率分布直方图中，小矩形的高等于每一组的频率/组距，它们与频数成正比. 小矩形的面积等于这一组的频率，且各个小矩形的面积的和等于1. 样本众数的估计值是图中最高矩形底边的中点的横坐标. 样本中位数的左边和右边的直方图面积相等. 样本平均数的估计值等于每个小矩形的面积乘以底边中点的横坐标之和.

药品效果观测

例3 为了比较A，B两种治疗失眠症的药的疗效，随机地选取20位患者服用A药，20位患者服用B药. 这40位患者在服用一段时间后，记录他们日平均增加的睡眠时间（单位：h），试验的观测结果如下.

服用A药的20位患者日平均增加的睡眠时间：

0.6 1.2 2.7 1.5 2.8 1.8 2.2 2.3 3.2 3.5

2.5 2.6 1.2 2.7 1.5 2.9 3.0 3.1 2.3 2.4

服用B药的20位患者日平均增加的睡眠时间：

3.2 1.7 1.9 0.8 0.9 2.4 1.2 2.6 1.3 1.4

1.6 0.5 1.8 0.6 2.1 1.1 2.5 1.2 2.7 0.5

（1）分别计算两组数据的平均数，从计算结果看，哪种药的疗效更好？

（2）根据两组数据完成下面茎叶图. 从茎叶图看，哪种药的疗效更好？

分析 对于（1），直接计算平均数，并比较大小. 对于（2），首先根据茎叶图的画法完成茎叶图，再比较茎叶图中数据的离散程度或中位数.

（2）由观测结果可绘制茎叶图如图：

由茎叶图可以看出，A药疗效的试验结果有的数据集中在茎“2.”，“3.”上，B药疗效的试验结果有的数据集中在茎“0.”，“1.”上，由此知A药的疗效更好.

点拨 茎叶图是一种常用的、形式简单易懂的统计图，它在实际生活中有着广泛应用. 画茎叶图时，对于重复的数据要重复记录，不能遗漏. 根据茎叶图作统计推断时，往往利用反映分布中心的指标或离散程度的指标来考虑，如中心指标可取平均数、中位数或众数，离散程度指标可求方差、标准差等.

统计思想在生活中应用极广，除了上面介绍的抽样方法与数据分析外，它还在回归分析等方面有着重要的用途，如生活中垃圾的无害化处理、产量的预测、天气预报、科学决策等. 我国著名数学家华罗庚曾这样说过：“宇宙之大，粒子之微，火箭之速，化工之巧，地球之变，生物之谜，日月之繁，无处不用到数学.”随着大数据时代的来临，统计思想无处不在，它已渗透到现实生活中的方方面面，其地位越来越重要. 相信在不久的将来，统计思想与方法必将与现代通信工具一样，成为人们生活中不可分割的一部分.