基于全景视觉机器人的改进UKF—SLAM算法研究

王开宇

摘 要：标准UKF-SLAM算法根据协方差矩阵计算的Sigma点会逐渐偏离真实状态估计值，影响定位精度。针对上述问题，该文引入平方根滤波的方法，在迭代更新过程中直接传递协方差矩阵的平方根，确保协方差矩阵的非负定性，提出了一种基于全景视觉的改进UKF-SLAM算法。并通过仿真实验，验证了该文提出的改进UKF-SLAM算法具有更高的定位精度。

关键词：全景视觉机器人 同时定位和地图创建 无迹卡尔曼滤波 平方根滤波

中图分类号：TP242 文献标识码：A 文章编号：1672-3791（2016）06（b）-0125-04

全景视觉传感器不仅具有普通视觉传感器信息量大、直观性好和采样周期短等优点，而且还具备全向360°的感知范围，在应用于同时定位与地图创建（SLAM）[1，2]是中时，视觉路标可在其视野范围内停留更长的时间，增强了对路标的连续观测和跟踪能力。

1988年，Smith，Self和Cheeseman在文献[3]中首次提出EKF-SLAM算法，利用EKF算法对机器人位姿和地图同时估计，奠定了移动机器人SLAM的理论框架。但EKF算法在执行时需要假设系统服从高斯分布，且存在线性化问题，无法满足模块化应用。Wang等[4]将UKF算法用于解决SLAM问题，在保证计算复杂度同阶的情况下，以对非线性函数的概率密度分布近似取代对非线性函数本身近似，解决了线性化问题。

然而UKF-SLAM算法中，每次迭代都需要传递协方差矩阵且根据协方差矩阵计算的Sigma点会逐渐偏离真实状态估计值，影响定位精度。针对上述缺点，该文提出了一种直接传递协方差矩阵平方根的改进UKF-SLAM算法，提高了算法的精度。

1 UKF-SLAM原理介绍

无迹卡尔曼滤波[5]（unscented Kalman filter，UKF）是一种利用采样策略对非线性分布进行逼近的方法，它以卡尔曼滤波框架为基础，利用UT变换，通过一组确定性采样点对非线性函数的概率密度分布进行近似。

1.1 UT变换

2 基于全景视觉机器人的改进UKF-SLAM算法

在标准的UKF-SLAM 算法中，每次迭代都需要传递完整的协方差矩阵用于计算点。当全景视觉机器人在多路标特征环境下，产生的Sigma点会逐渐偏离真实状态估计值，影响定位精度。平方根滤波可以解决状态和参数的估计问题，提高UKF算法的计算效率。将平方根滤波思想引入UKF-SLAM算法中，使其在迭代更新过程中，通过传递协方差矩阵的平方根代替直接传递协方差矩阵，既可以提高UKF-SLAM方法的鲁棒性，同时也能保证协方差矩阵的非负定性。为此，该文提出了一种基于平方根滤波的UKF-SLAM算法，并用其解决全景视觉移动机器人的SLAM问题。

2.1 平方根UKF算法原理

Rudolph和Eric等首先将平方根滤波的思想引入UKF方法，并解决了状态和参数的估计问题，平方根UKF算法中利用三种运算技巧提高算法的运行效率[6]，如下：

（1）分解。UKF算法中，若，可通过Cholesky分解得到，而采用QR分解可以提高算法的运行效率。

（19）

采用分解不必先求出样点的加权方差再进行分解，还降低了计算量[7]。这对SLAM在真实环境实验的实时性要求是非常有必要的。

（2）Cholesky因子更新。若的Cholesky因子为，则的Cholesky 因子就可由表示。

（3）最小二乘法。UKF算法需求逆，因上三角矩阵是半正定的，所以引入回代法求解上式，以免去求逆运算。

2.2 基于全景视觉机器人的平方根滤波UKF-SLAM算法

因为平方根UKF算法的改进，使原算法的状态向量和协方差矩阵都不必在经过噪声增广。假设系统噪声和观测噪声均为高斯噪声，下面对该文提出的基于全景视觉的改进平方根UKF-SLAM算法进行介绍。

3 实验及分析

该节分别对基于全景视觉移动机器人的标准EKF-SLAM、标准UKF-SLAM这两种传统卡尔曼滤波框架下的SLAM算法和该文的改进UKF-SLAM算法进行仿真实验，通过对全景视觉移动机器人定位精进行比较分析，进而验证该文所提出的基于全景视觉移动机器人的改进UKF-SLAM算法的优势。

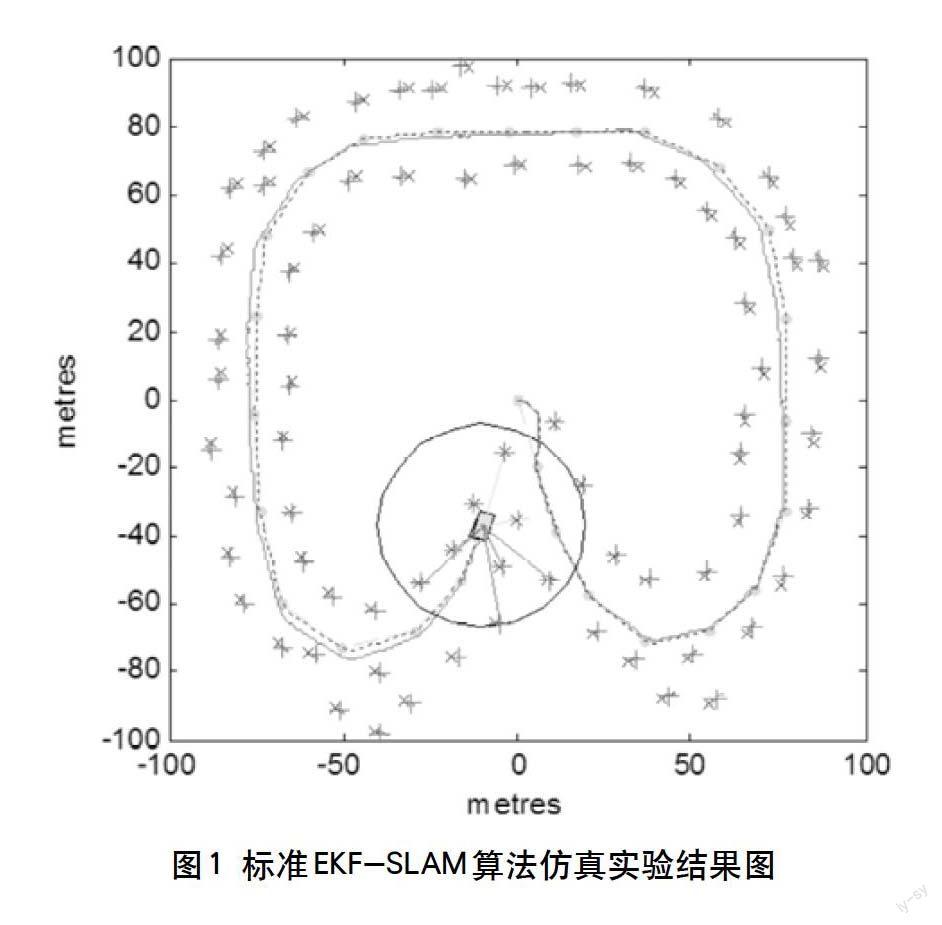
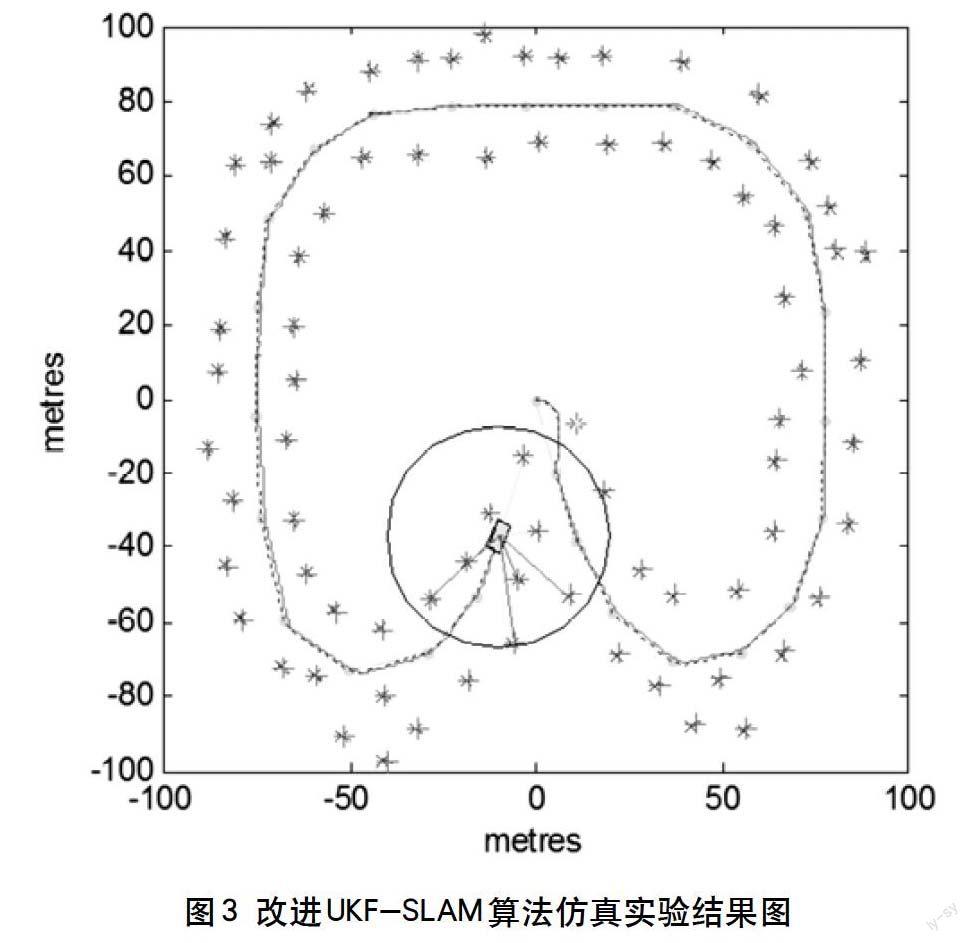
仿真在200 m×200 m的矩形区域中进行，该区域中分布着若干环境特征点，用蓝色“*”表示；在实验中提前规划了全景视觉机器人的行驶路线，全景视觉机器人的行驶路线（图1、图2、图3中绿色线）由27个路径点（用绿色“”表示）确定。

图1、图2和图3为标准EKF-SLAM、标准UKF-SLAM同该文的改进UKF-SLAM的仿真结果。图1、图2、图3中，绿色线是按路径信息设置好的全景视觉机器人运动轨迹；蓝色虚线表示机器人实际运动轨迹；红色线表示机器人利用SLAM算法之后得到的估计更新后的轨迹；蓝色“×”表示预先设定好的地图中的特征，即实际的路标，是静止的；红色“+”表示机器人经过SLAM算法得到的环境中路标估计位置；红色椭圆表示机器人对路标误差的估计，椭圆的大小代表了对应路标的不确定程度。矩形代表机器人，蓝色的矩形表示机器人在控制信息下到达的实际位置，红色矩形表示机器人在SLAM算法下所估计的位置。

机器人从（0，0）点出发，沿行驶路线按逆时针方向行驶1周。运动过程中利用外部全景视觉传感器对周围环境进行扫描，获取观测信息，同时根据全景视觉移动机器人的控制输入得到自身轨迹状态的预测信息，根据观测信息和预测信息，利用SLAM算法最终得到全景视觉移动机器人的运行轨迹和环境地图。

图4、图5为分别使用三种SLAM算法获得的全景视觉机器人定位误差对比情况。横轴为SLAM的运行时间，纵轴为全景视觉机器人在X和Y方向上的位置偏差。总体上从曲线中可以看出，三种算法都具有较小的估计误差，且具有收敛性，由此表明，这三种SLAM算法能有效实现自主定位。对比三种算法，标准EKF-SLAM的定位误差最大，X方向的最大误差为2.63 m，Y方向的最大误差为2.27 m；标准UKF-SLAM的定位精度高于标准EKF-SLAM，X方向的最大误差为1.54 m ，Y方向的最大误差为1.51 m；该文采用的改进UKF-SLAM算法在X方向的最大误差为0.54 m，Y方向的最大误差为0.47 m，在整个全景视觉机器人运行过程中其估计精度都保持在较高水平，算法的定位精度最高。仿真实验结果与前文的理论分析一致。

4 结语

该文主要研究小尺度室内环境的全景视觉移动机器人SLAM算法。针对UKF-SLAM中每个时刻都需要传输协方差矩阵计算的Sigma点会逐渐偏离真实状态估计值的问题，引入平方根滤波的方法，提出了一种基于全景视觉的改进UKF-SLAM算法。仿真实验表明，与标准EKF-SLAM和UKF-SLAM算法相比，该文提出的改进UKF-SLAM在对全景视觉机器人自身的定位具有更好性能。

参考文献

[1] 梁志伟，马旭东，戴先中，等.基于分布式感知的移动机器人同时定位与地图创建[J].机器人，2009，31（1）：33-39.

[2] 吴叶斌.基于全景视觉的移动机器人SLAM方法研究[D].哈尔滨工程大学，2011.

[3] Smith R， Self M， Cheeseman P. Estimating Uncertain Spatial Relationships in Robotics[M].New York：Springer Verlag，1988：167-193.

[4] Wang H， Fu G， Li J， et al. An adaptive UKF based SLAM method for unmanned underwater vehicle[J]. Mathematical Problems in Engineering，2013（4）：1-12.

[5] 杜航原.自主式水下航行器同步定位与地图构建算法研究[D].哈尔滨工程大学，2012.

[6] Van D M R， Wan E A. The square-root unscented Kalman filter for state and parameter-estimation[C]// Icassp，2001：3461-3464.

[7 成兰，谢恺.迭代平方根UKF[J].信息与控制，2008，37（4）：439-444.