幸福数学课,师生齐欢乐
2016-05-30吴德志
吴德志


【摘 要】新一轮课程改革中,提出了教育应以人为本的先进理念,以人的和谐发展为目标,希望人的本性、人的尊严、人的潜能在教育过程中得到最大的实现与发展,最后达到人人都拥有幸福人生,这是我们教育的终极目标。因此,追求数学课堂教学的“幸福度”,成了数学课堂教学追求的目标之一。让数学课堂洋溢着幸福,应该是我们数学课堂教学的核心意义,也是我们数学教师一生的追求。
【关键词】幸福;数学课;师生;齐欢乐
一、幸福数学课堂的必要性
生活幸福是每一个人的基本追求,幸福地学习也是所有学生的理想。但现实的教育中,中学生在应试教育的体制下,面对繁重的学业任务,无疑是压力最大的一个群体。他们一天当中大多数时间是在学校课堂中度过的,整日面对的就是做不完的练习题以及上不完的复习课。在这种情形之下,他们就无课堂幸福感可言。所以学校和教师应采取相应的措施,增强学生的数学课堂幸福体验。
二、幸福数学课堂源于教学设计
著名教育家苏霍姆林斯基说:“在教学大纲和教科书中,规定了给予学生各种知识,却没有给予学生最重要的东西,这就是──幸福。”在备课时,我们应问问自己:如何设计才能使学生觉得幸福呢?在上完课后要问问自己:这堂课你幸福吗?对学生和老师来说幸福比成功更重要,成功只是幸福的来源之一,而不是幸福的全部,成功只是手段,幸福才是目的。 要想让学生在课堂上感受到幸福,必须知道学生到底要的是什么。让教学设计满足学生的需要,让课堂活动符合学生的需要,让学习过程不枯燥无味。
三、幸福数学课堂源于教师的帮助
幸福需要人设置,需要人呵护。特别是当学生在学习上遇到难处时,多么希望老师给予提示、提醒。不少课堂上,老师似乎为了体现启发性,或者某种目的,抛出一个或几个问题,还美其曰,提高学生独立思考能力。由于学生生活经验,知识基础,感悟能力等因素,不可能发展得一样齐,或者不能和已是成人的老师一样聪明,懂得那么多。吊吊胃口可以,让学生适当想想也可以,让一部分学生多想想也可以,问题是不是所有学生都能想得出来?随着课程改革的推进,我们越来越感觉到:新教材“加快了”学生的两极分化,导致了“强者更强,弱者更弱”,使部分学生过早地丧失了学习数学的兴趣,成了老师和家长非常担忧的“学困生”。而作为直接实施新课改的一线教师,在无力改编教材的前提下,能为这些暂时处于“弱势群体”的学生做些什么呢?我的体会是:把更多的爱倾注给学困生,在教学的每一环节都创设相互尊重、自然和谐的学习氛围,时时处处想到他们,关心他们,帮助他们找到自信,让他们真正学有所获,感觉到数学课堂的幸福。
四、幸福数学课堂源于用心地倾听
幸福的课堂绝不是“填鸭式”、“注入式”、“一言堂”的课堂,幸福的课堂是以人为本的对话与分享的课堂。对话还需要聆听,学生在聆听中分享教师的情感,教师在聆听中感受学生的心跳,沟通学生的体验。课堂教学中师生应该是学生式的教师与教师式的学生。老师与学生间能进行平等的精神交流,学生是学习的主体,在课堂上可以张扬个性,展现创造力。教师上课不仅仅是传授知识,而是一种分享和理解,更多时候是聆听者,建议者,分享者,情感导引者,师生共同成长的体验者、陪同者、见证者。
例如:如图,在△ABC中,已知AD是BC边上的中线,且AD=BC.请判断△ABC是什么三角形?并说明理由.
有个学生马上回答△ABC是直角三角形,理由是因为AD=BC,所以△ABC是直角三角形。我问他有这个判定吗?他回答说没有,但是我们学过直角三角形斜边中线等于斜边的一半这一性质,所以只要一边上的中线等于这条边的一半,它一定是直角三角形。
我倾听完学生的发言后,并没有马上否定学生的答题理由,而是问他既然没有这样的判定,你是否可以通过从已知出发,把解题的详细过程说出来?学生马上回答说可以。
∵AD=BC,
∵AD是BC边上的中线
∴BD=CD=BC,
∴AD=BD=DC,
∴∠B=∠BAD,∠C=∠CAD,
∵∠B+∠BAD+∠CAD+∠C=180°,
∴∠BAD+∠CAD=90°,
即∠BAC=90°.
当学生回答完之后,我再总结,由于没有在三角形中一边上的中线等于这条边的一半时,这三角形是直角三角形的判定,所以我们只有通过推理论证出来才可以。这样顺藤摸瓜既让学生很快地纠正了错误,而且还能保护学生的积极性。所以在数学课堂教学中,教师要在倾听中捕捉宝贵的教学机遇,好好加以利用,才能与学生产生心灵的共鸣,让数学的课堂幸福起来。
五、幸福数学课堂源于探索
数学是一门特别注重思维过程教学的学科,数学是理性的,思维严谨的课程。很多时候数学教学会陷入枯燥地怪圈。叶澜教授说:“课堂上,教师要封住自己的嘴,让自己少说一点,留出时间和空间给学生。”教师做好助演,引导、点拨、释疑,突出培养学生良好的思维习惯、品质;学生担当主演,走进数学世界,以自主、合作、探究的方式开展发现、分析、解决问题的活动,让学生去经历知识的形成过程,在此过程中引导他们积极地去探索知识、发现规律,并掌握学习方法,逐步使他们形成自主探索知识的能力。这就是每一位教师、每一位学生、每一位家长所渴望的、所追求的幸福教育。
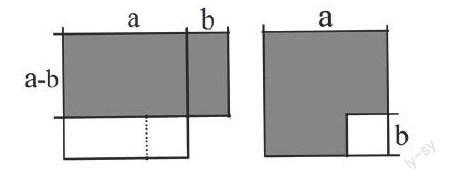
例如在讲授平方差公式时,我先引导学生探究在大正方形内截取一个小正方形后剩余的面积如何表示,再让学生小组讨论“如何计算两图中阴影部分的面积?”通过动手“剪一剪”、“拼一拼”,自主发现“面积相等”。再通过一个游戏“谁的眼睛亮?”,观察出:(a+b)(a-b)=a2-b2这个规律,从而总结出平方差公式。然后再根据多项式乘以多项式的法则从代数角度证明公式的成立。这样就从几何以及代数两个角度来证明公式,使学生感受到几何与代数的内在联系。
这样数学课堂不再是单调的背公式和繁琐做题,不再是为了单纯地传授知识,而是注意让学生参与平方差公式的探究推导、归纳证明。这样做极大的激发了学生的学习兴趣,又培养了学生的自主探究能力,使学生尝到了由自主学习而获得新知的喜悦,在探索中感受幸福。
六、幸福数学课堂源于自由展示
我们常说,把课堂还给学生,其实就是要把学习的主动权还给学生,让学生成为课堂的主人。如今,学生获得知识信息的渠道多样化了,教师要做的不只是传授现成的教科书上的知识,而是指导学生懂得如何获取自己所需要的知识。针对中学生学习的实际,数学老师上课的关键在于让学生快乐地、努力地参与到课堂教学中去,不断让学生思考,不断迎接挑战。在幸福课堂上,学生也可以成为临时老师,学生的任何思维、想法都可以共享。在分享中,教师与学生都能够彼此享受到尊重的幸福,交流的幸福,成长的幸福。
如讲直角三角形斜边中线等于斜边的一半这一性质时,我并没有叫学生直接死记硬背这一个性质,而是先让学生将文字语言转换成数学符号语言,在直角三角形ABC中,∠BAC=90°,AD是斜边BC的中线,求证:AD=BC。然后让学生分小组讨论,最后派代表上台讲解,有不同证明方法时都可以依次上台展示。下面是学生展示的几种不同证法。
【证法1】延长AD到E,使DE=AD,连接CE。
∵AD是斜边BC的中线,
∴BD=CD,
又∵∠ADB=∠EDC,
AD=DE,
∴△ADB≌△EDC,
∴AB=CE,∠B=∠DCE,
∴AB//CE
∴∠BAC+∠ACE=180°
∵∠BAC=90°,
∴∠ACE=90°,
∵AB=CE,∠BAC=ECA=90°,AC=CA,
∴△ABC≌△CEA(SAS)
∴BC=AE,
∵AD=DE=AE,
∴AD=BC。
【证法2】取AC的中点E,连接DE。
∵AD是斜边BC的中线,
∴BD=CD=BC,
∵E是AC的中点,
∴DE是△ABC的中位线,
∴DE//AB
∴∠DEC=∠BAC=90°
∴DE垂直平分AC,
∴AD=CD=BC。
【证法3】延长AD到E,使DE=AD,连接BE、CE。
∵AD是斜边BC的中线,
∴BD=CD,
又∵AD=DE,
∴四边形ABEC是平行四边形,
∵∠BAC=90°,
∴四边形ABEC是矩形,
∴AE=BC,
∵AD=DE=AE,
∴AD=BC。
【证法4】 作AB、AC的中点E、F,连接ED、DF,
∵BE=EA,BD=DC,
∴ED∥AC,又∵A=90°,
∴BED=90°,
∵∠BED=∠AED=90°,BE=AE,ED=ED
∴△BED≌△AED,
∴BD=AD,同理可证△ADF≌△CDF,
∴AD=CD,
∴AD=BD=CD,
∴AD=BC。
在这个过程中,学生不仅懂得了如何证明直角三角形斜边中线等于斜边的一半,同时体会了同一个题目的不同思路及不同证明方法,积累了数学活动的经验。整个过程让学生动口,又动手,这样课堂活起来了,学生动起来了:敢想、敢问、敢说、敢做、敢争论,充满着求知欲和表现欲,课堂处处洋溢着幸福。
七、幸福数学课堂源于学有所获
长期以来,初中数学教学,由于受班级授课制的束缚,教师从备课、授课、作业、考查到评价,很少顾及程度好、中、差各类学生的智能差异,均采用“一刀切”的方法进行教学,使得优生吃不饱,程度差学生吃不了,中等生吃不好。随着九年义务教育的深入实施,教学更加需要从义务教育的性质、任务上全面考虑初中数学教学的目的和任务,以便更主动积极地适应社会和科学技术发展的需要。我在课堂教学中,实施“分层递进”教学法,最大限度地考虑学生的个体差异和内在潜质,培养优等生,转化学困生,充分调动了学生学习的积极性和主动性,满足了学生不同层次的学习需求,使每个层次的学生都能得到最优的提高和发展。学生的一点发现,一点创新,一点收获,一点意想不到,都能成为“成就”,都能引起兴奋,都能成为幸福的“引爆点”。
幸福是一种追求,幸福是一种意识,幸福是一种存在,幸福是一种渴望,幸福更是一种信念。让学生在数学课堂中感受到学习的幸福,是我们的责任和义务。让我们在心灵里点亮幸福的灯盏,用崭新的理念,饱满的激情,无穷的智慧,去实践幸福的课堂,拥抱幸福的明天。只要理想不灭,幸福,就在灯火阑珊处!
