基于有限元分析的某型设备温度场数值仿真研究

韩东霏　陈典斌　马俊英　王芳

摘 要：步入式试验室与现有技术标准指导的小型试验箱相比，在参数检测条件、被试品评定等方面具有针对性指导的相关技术方法较少，且现有温度试验技术零散，缺乏系统性、规范性和针对性。针对上述理论原因并结合试验实际情况，对两种典型设备开展温度场仿真建模，从数值计算基础上进行了温度场的数值分析，得到了其温度分布云图并给出了准确的内、外部温度稳定时间，解决了实际试验中温度稳定时间难确定的问题，并在理论上提供了数据支撑，为下一步开展理研项目研究奠定理论基础。

关键词：保温时间 升降温时间 热平衡时间 温度场 数值仿真

中图分类号：TN249 文献标识码：A 文章编号：1674-098X（2016）06（b）-0042-03

过保温会引发设备相关结构部件的尺寸和形状产生热变形误差，产生机械故障而使其性能下降和使用寿命降低。国军标GJB150A[1]、美军标MIL-STD-810F[2]和英军标DEF 07-55[3]提出用直接测量法来确定设备在高低温环境中适应能力。但人工测量费时费力，若采用放置温度传感器的方法，对不同结构的设备，复杂程度不同。若要求精确得到试验温度稳定时间，对温度传感器数量的确定、放置位置的细化选择是否科学合理（包括能否放置进精密仪器内问题、放置后对试验的影响、舱门和箱盖能否关闭）等多种问题可能同时存在。GJB150的修订版GJB200X[4]强调新的设备环境试验标准在试验程序的选取和试验方案的制定上的剪裁性。目前国内对温度试验技术及温度环境对设备影响的相关研究还不够全面。若要在试验前确定试验温度稳定时间，目前尚无结构模型可以衡量，也无基础性科学研究和理论数据支撑。

1 数值仿真研究

1.1 数学计算分析[5]

（1）内部微分方程，非稳态、具有内热源的设备内部导热微分方程为：

式（1）中：T=T（x，y，z，t）（K）为热力学温度分布函数；t（s）为时间；λ（W/（m·K））为微元材料的导热系数；微元材料单位质量定压热容为（J/（kg·K））；微元物质的密度为ρ（kg/m3）；（W/m3）为微元单位体积的热生成率。由式（1）可知，发生导热过程的设备内任意一点的温度随时间和空间的变化取决于其各部分材料的导热系数、比热容、密度和热生成率。

（2）外部微分方程，武器装备外表面与试验箱内空气之间通过对流和辐射方式进行热交换，属于第三类边界条件，换热规律表达式如式（2）所示：

为外表面法向的单位矢量；α（W/（m·K））为外表面与试验箱内空气之间的对流传热系数；（K）为试件外表面的热力学温度；（K）为试验箱内空气热力学温度；ε为系统黑度，亦称辐射系数；（W/（m2·K4））为波尔兹曼常数，其值为5.67×10-8；为辐射角系数即形状因子。

（3）有限元矩阵，在有限元热分析系统中，热传递温度场控制方程见式（3）：

式（3）中：[C]为比热矩阵；{}为节点温度的时间导数；{T}为节点温度向量；[K]为有效传导矩阵；{Q}为有效的节点热流率向量。根据式（3），再根据边界条件和初始条件，可在数值分析软件中求出温度试验时试件温度场的有限元近似解。

1.2 研究对象及模型建立

通过查阅国内外近几年来的相关技术资料[6-9]，了解温度场机理、工作流程及步骤。结合几种典型武器装备，建立可调整结构模型，仿真分析主要从以下几个方面进行。

（1）材料设置，炮体选用52Mn，精密电子仪器部件可简化为灌封材料聚氨酯、高频线路板，材料属性可查。

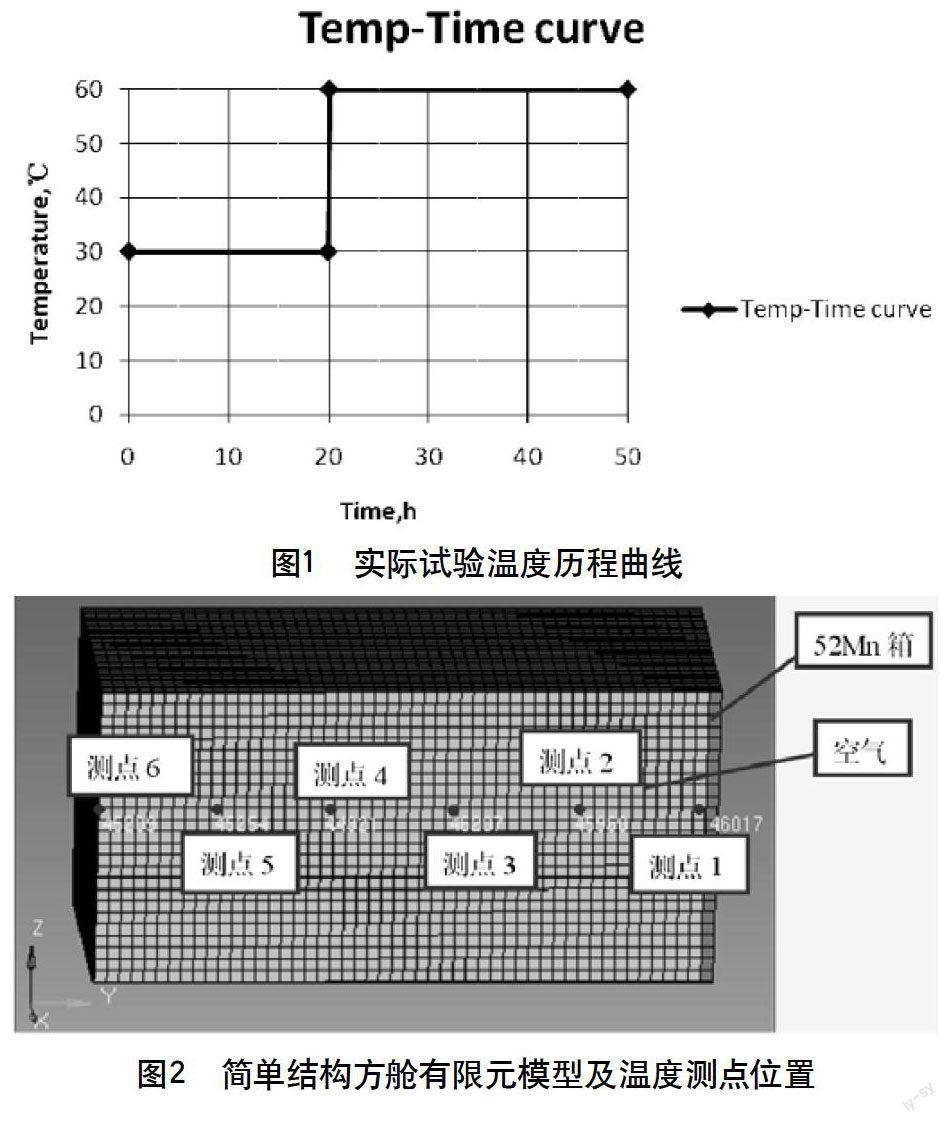
（2）边界条件，初始温度设置为室温25 ℃。为保证足够长的计算时间使所有位置温度达到平衡，经试算确定模型外表面温度加载历程如图1所示。

按照实际试验曲线，当空间温度达到30 ℃时，保温20 h；再经过升温到60 ℃，保温30 h。

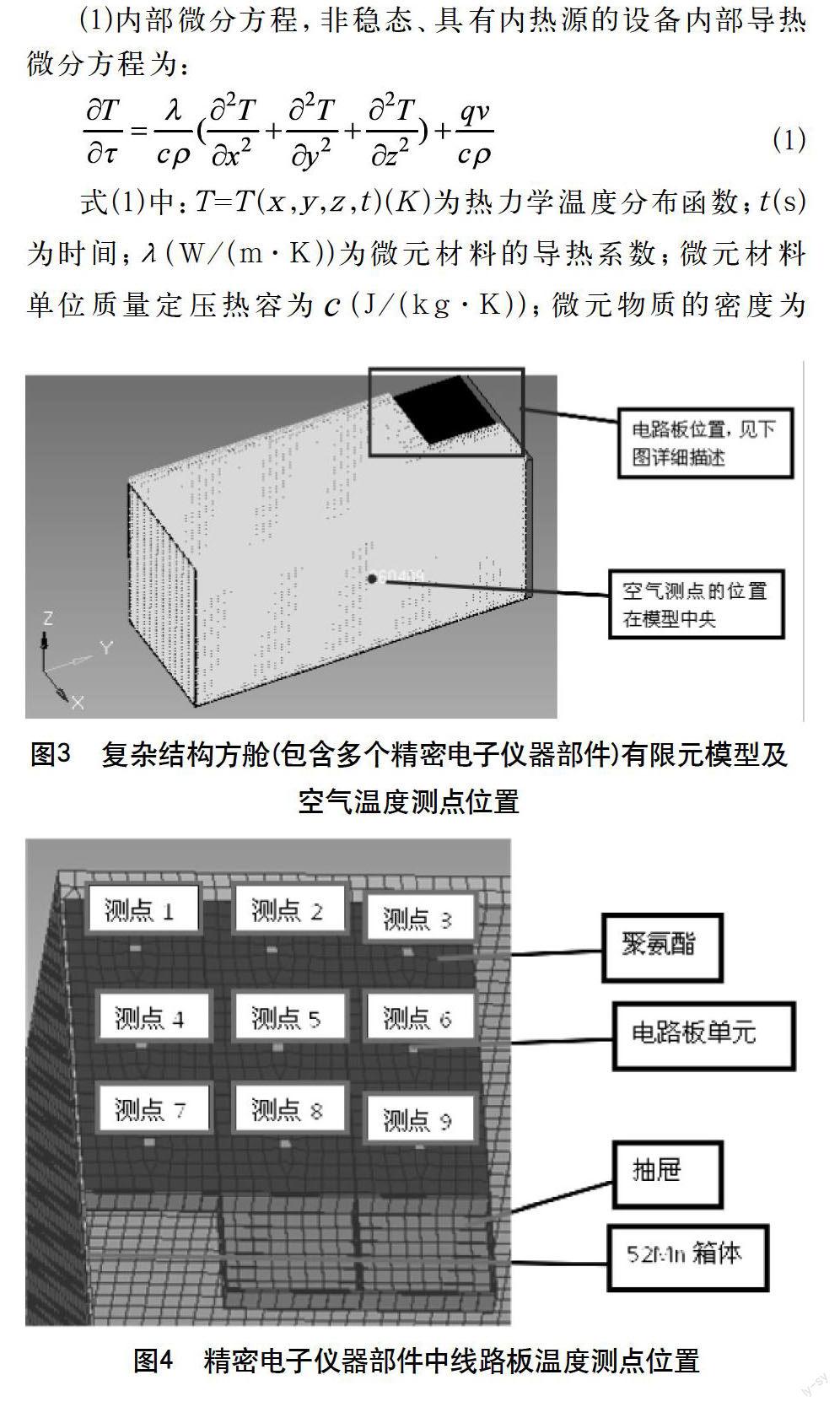
（3）仿真建模及测点分布，为证明开展“基于有限元分析软件的武器装备温度场数值仿真研究”的可行性，该报告以两种结构方舱为例进行模型建立和布置测点，如图2、3和4所示。

图2为简单结构方舱有限元模型及温度测点位置示意。从测点1到测点6沿右侧方舱壁—空气—左侧方舱壁的途径横贯整个简单结构方舱中部。

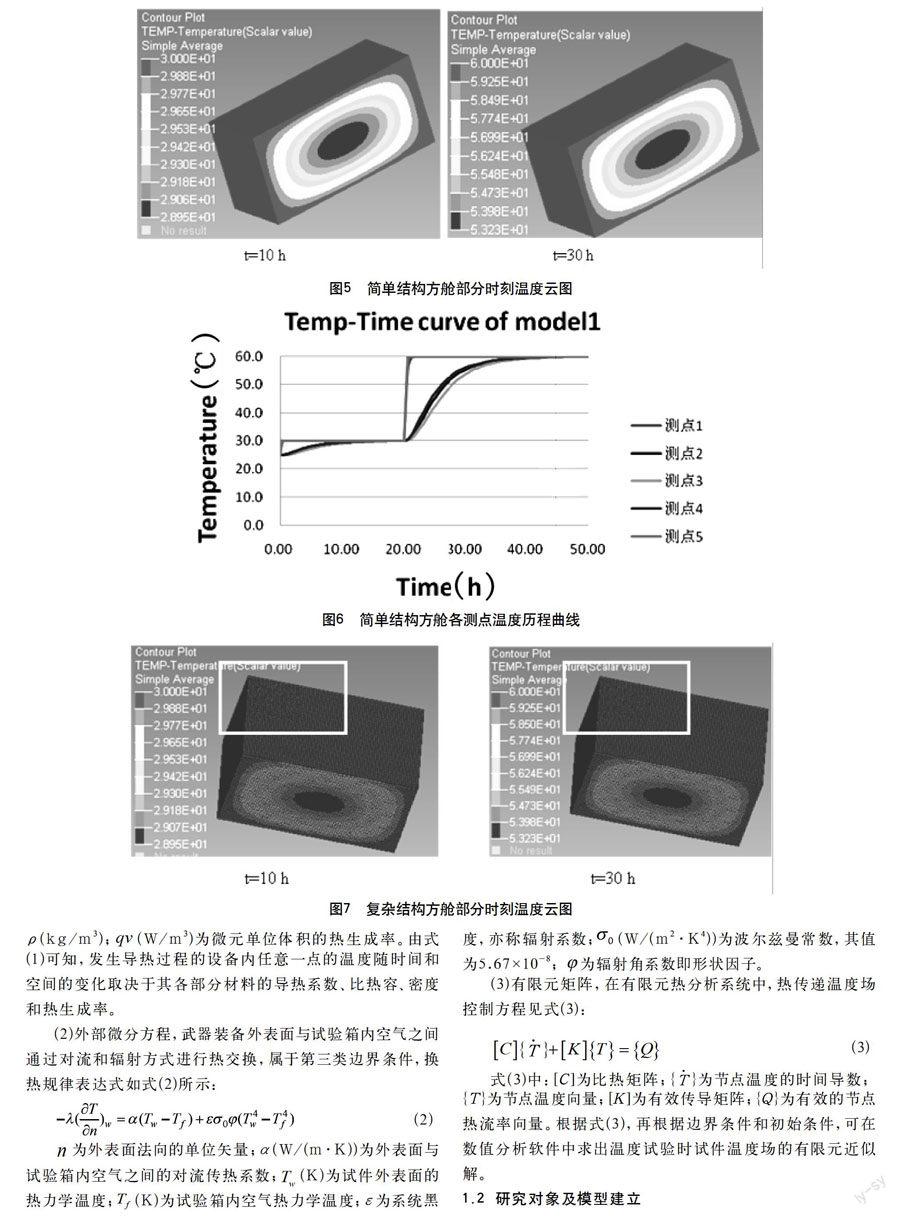
图3为复杂结构方舱模型及温度测点位置示意。空气测点位于模型中央处，电路板在模型内部，外部不可见。

图4为精密电子仪器部件测点位置分布示意。精密电子仪器部件装载在各个薄壁箱体中，聚氨酯为填充材料，电路板为主要组成部分，温度测点位于箱体中部。

2 计算结果

2.1 简单结构方舱

简单结构方舱部分时刻温度场云图如图5，各测点温度历程曲线如图6。

结果分析：简单结构方舱模型靠近箱体壁面的测点1和测点5最先达到温度平衡，加载30 ℃时，10 h后所有节点温度都已在29.2 ℃以上，之后缓慢进入平衡状态；温度加载60 ℃时，10 h后所有温度在59.3 ℃以上，之后缓慢进入平衡状态。

2.2 复杂结构方舱

复杂结构方舱部分时刻温度场云图如图7，各测点温度历程曲线如图8。

结果分析：模型2中线路板测点离上箱面较近，加载30 ℃时，线路板测点1、2、3、4在2.83 h时温度已达30 ℃，随后0.5 h内，所有线路板测点温度达到平衡温度30 ℃；加载60 ℃时，5 h后线路板测点1、2、3、4达到平衡温度60 ℃，随后1.5 h内，所有测点达到平衡温度60 ℃。模型2中空气测点加载30 ℃时18.8 h温度平衡，加载60 ℃时，28 h后温度平衡。

3 结语

为对武器装备建立某种可调整结构的有限元模型，在试验前与主持单位及厂家进行曲线合理性分析，解决温度场分布及热应力应变场分布问题。该文以上述两种结构方舱的散热设计分析为例，进行数值仿真分析，结果表明：在温度变化情况下，试验线路板部件等重要测试部件内部会产生热应力、应变，是其结构破坏的重要影响因素。后期若进一步研究，可以此次分析模型温度场结果为边界条件，进行线路板或线路板安装的子模型热应力耦合分析，得到详细温度加载过程热应力应变结果，进一步对其结构稳定性进行评估。

参考文献

[1] 中国人民解放军总装备部.GJB 150.3A-2009，军用装备实验室环境试验方法第3部分：高温试验[S].北京：总装备部军标出版发行部，2009：1-8.

[2] 美国国防部.MIL-STD-810F，国防部试验方法标准-环境工程考虑和实验室试验[S].2006.

[3] 英国国防部.DEF 07-55，国防部试验方法标准-环境工程考虑和实验室试验[S].2007.

[4] 中国人民解放军总装备部.GJB 200X，军用装备实验室环境试验方法第3部分：高温试验[S].北京：总装备部军标出版发行部，2009：1-8.

[5] 杨世铭，陶文铨.传热学[M].北京：高等教育出版社，2011.

[6] 李楠，张东方，陈东哲.电子元件散热的数值模拟[J].能源与节能，2012（5）：79-81.

[7] 徐少亭.基于蚁群算法的PCB板电子元件热布局优化研究[D].四川：电子科技大学，2012.

[8] 李静，姬升涛，刘建勇，等.电子元件热装置的烟囱效应分析[J].电子与封装，2011，11（6）：36-40.

[9] 马占龙，王高文，张健，等.基于有限元及神经网络的磨削温度仿真预测[J].电子测量与仪器学报，2013，27（11）：

1080-1085.