神经网络校正的卡尔曼滤波算法在车辆GPS/DR组合定位系统中的应用

郑定富 匡磊

摘 要：航位推算（Dead-Recking，简称DR）和全球定位系统（GPS）是车辆定位与导航系统中应用最广泛的两种定位技术。针对GPS和DR各自的特点，车辆定位系统常采用GPS/DR组合定位方案与单独的DR系统定位方案，采用信息融合技术来组合GPS系统和DR系统，使得GPS/DR组合后的定位与导航系统的性能要优于各个子系统的性能，由基本Kalman滤波算法而派生出的扩展的Kalman滤波算法可以解决实际工程中的非线性滤波问题，本文提出的BP神经网络的非线性映射能力修正的扩展的Kalman滤波算法性能要优于传统的基本Kalman滤波算法。

关键词：组合导航信息融合；Kalman滤波；BP神经网络

1 前言

車辆导航与自动驾驶需要精确地知道车辆的位置信息和速度信息。GPS卫星定位系统通过接收机可以在全球范围内提供用户精确的位置信息。然而，GPS测量中几种误差的存在使其具有良好的长期误差特性而具有较差的短时误差特性。对很多导航用户来说，GPS作为单个独立的导航系统是不够的。由GPS和其他导航方式通过数据融合组成的导航系统是一种较为理想的选择。在GPS/DR组合定位系统中，多传感器的信息融合是根据系统的物理模型（由状态方程和测量方程来描述）和系统模型（即传感器噪声的统计假设），将量测数据映射到状态矢量空间。其中，状态矢量包括一组目标载体定位的变量，如位置、速度、加速度和角速度等，通过描述载体的状态，精确测量载体的运动行为。GPS/DR组合定位系统的数据融合就是可以根据量测数据给出一个状态的最优估计量。通常，多个传感器可以具有不同的物理模型。在车辆GPS/DR组合定位系统中，Kalman滤波是应用最为广泛的数据融合算法。但是对组合导航系统中具有非先验性的噪声的情况，传统的Kalman滤波不是很有效，用BP神经网络来辅助调节Kalman滤波，可使其具有自适应能力以应付动态环境的扰动。

2 GPS/DR组合系统状态方程和观测方程的建立

建立系统状态方程存在的一个难点是如何描述车辆的加速度变化。采用机动载体的“当前”统计模型来描述车辆加速度的统计分布。这种模型的意义在于，在每一种具体的场合，人们仅关心机动加速度的“当前概率密度”，即目标机动的当前可能性，当目标以某一加速度机动时，它在下一时刻的加速度取值范围是有限的，并且只能在“当前”加速度的邻域内，即

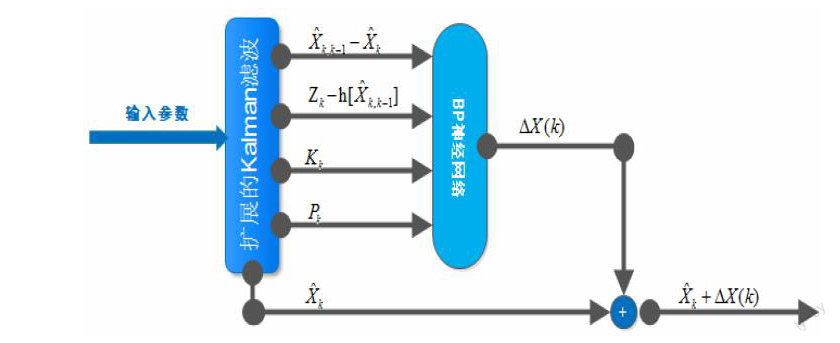
使用上式在实际的非线性系统中滤波时必定会产生较大的误差，甚至发散。因此需要用BP神经网络来校正。把能直接影响Kalman滤波估计的误差的参数作为神经网络的输入，由其下3部分组成：①状态预测值与状态估计值之差；②观测值与估计观测值之差；③Kalman滤波增益；④协方差PK。BP神经网络的期望输出值为，其中E为目标状态向量的理论值。BP神经网络经过这样的训练后，把网络输出的与经过Kalman滤波的结果相加，便可以得到精度更高的结果。基于BP神经网络修正的扩展的Kalman滤波算法的原理框图如图1所示。

4 仿真结果

输入输出层的神经元的个数由输入输出向量的维数决定。理论证明，在任何闭区间内的连续函数都可以用三层BP神经网络逼近，因此本文采用单隐层BP神经网络，隐层神经元个数由公式来确定。其中，N和M分别为输入和输出单元个数，a为[1 10]之间的数，a的最优值由实验测试决定——可以将隐层神经元个数当成一个参数，通过一个循环得出范围内所有的结果。经测试，最优值为16。仿真结果如图2所示。

5 结论

从图1可以看出，在东向和北向上的位移误差，经BP网络校正的扩展的Kalman滤波比之前的经典的扩展的Kalman滤波要小。本文提出的BP神经网络修正的扩展的Kalman滤波算法优于传统的扩展的Kalman滤波算法，在组合定位中拥有更好的性能和更广泛的应用前景。

参考文献

[1]Salmon D.C.，Bevly D.M..An exploration of low-cost sensor and vehicle model solutions for ground vehicle navigation[A].Position，Location and Navigation Symposium-PLANS 2014，2014 IEEE/ION[C].2014：462-471.

[2]Kim D.J.，Kim M.K.，Lee K.S.，et al.Localization system of autonomous vehicle via Kalman filtering[A].Control，Automation and Systems（ICCAS），2011 11th International Conference on[C].2011：934-937.

[3] 赵琳，王小旭，丁继成，等.组合导航系统非线性滤波算法综述[J].中国惯性技术学报，2009，17（1）：46-52.

[4] 赵艳飞，张树君.车载 GPS/DR 组合导航系统的 DR 算法[J].科技资讯，2013，（22）：8-10.

[5]Heeger D.J.，Hager G..Egomotion and the stabilized world[A].Computer Vision.，Second International Conference on[C].1988：435-440.

[6]Groves P.D.Principles of GNSS，inertial，and multisensor integrated navigation systems[M].Artech house，2013.

[7]Khaleghi B.，Khamis A.，Karray F.O.，et al.Multisensor data fusion：A review of the state-of-the-art[J].Information Fusion，2013，14（1）：28-44.

[8]He W.，Lian B.，Tang C..GNSS/INS integrated navigation system based on adaptive robust Kalman filter restraining outliers[A].Communications in China-Workshops（CIC/ICCC），2014 IEEE/CIC International Conference on[C].2014：32-35.

[9]邓自立.Wiener滤波，Kalman滤波和信息融合滤波理论研究进展[J].黑龙江大学工程学报，2011，（3）：37-44.

[10]德钧，房建成.GPS 动态滤波的理论，方法及其应用[M].江苏科学技术出版社，2000.

[11]Singer R.Estimating optimal tracking filter performance for manned maneuvering targets[J].Aerospace and Electronic Systems，IEEE Transactions on，1970，（4）：473-483.

（作者单位：华中科技大学自动化学院）