统计过程控制在石英晶体振荡器数据分析中的研究应用
2016-05-30王振晓曹丹阳
王振晓 曹丹阳


摘 要:石英晶体振荡器在准确度和稳定度方面要求极高。以准确度的数据作为分析对象,采用均值—极差统计过程控制方法进行数据处理分析,通过绘制均值—极差控制图,以及对生产过程能力指数Cp和Cpk的计算,来判断晶体振荡器在频率准确度方面的过程加工质量方面的能力。该方法可以为石英晶体振荡器的其他的部分参数的质量控制起到一定的借鉴作用;同时为计算机在石英晶体振荡器频率准确度数据分析方面的应用起到了理论作用。
关键词:石英晶体振荡器;频率准确度;均值极差控制图;过程能力指数
0 引言
石英晶体振荡器作为一种准确度和稳定度都极高的一类振荡器,被广泛应用于军事和宇航领域、科研与计量领域以及工业、消费、汽车等领域。石英晶体振荡器涉及的参数很多,其中频率准确度和温度稳定度与与其他指标相比是晶体振荡器的一个关键质量特性。因此,在对整个生产过程的Cp和CPK设计中,会更加关注于晶体振荡器的频率准确度,通过对频率准确度数据的统计过程控制,来推断生产的过程能力,从而控制产品频率准确度这种作为晶体振荡器的重要特性的质量。
1 统计过程控制
统计过程控制就是应用统计技术对过程进行评估监控,建立保持过程处于可接受的并稳定的水平,从而保证产品与服务符合规定要求的一种质量管理技术 [1]。现在一般采用6σ控制方式,即过程均值无偏移的情况下的不合格频率为2ppb,过程均值偏移1.5σ的情况下的不合格频率为3.4ppm。
统计过程控制进行步骤:(1)控制图的设计;(2)采用什么样的控制图;(3)过程能力指数的运算,(4)结论。
2 石英晶体振荡器频率准确度
2.1 频率准确度的定义
所谓频率准确度则是指标称电源电压、标称负载阻抗、基准温度(25℃)以及其他条件保持不变,晶体振荡器的频率相对与其规定标称值的最大允许偏差,频率准确度是指振荡器实际的频率值fx对其标称值f0的相对偏离,即e=(fx-f0)/f0 [2]。单位是PPM或PPb,是一种离散变量。
2.2 频率准确度数据的特点
①理想状态下是以均值μ = 0的正态分布。在此基础上σ越小越好。即总体质量特性服从正态分布,即x~N(μ,σ2),式中μ表示样本的均值,σ表示样本的标准偏差
②如果用直方图来表示,则该数据需要符合对称型的直方图。即中间高,两边低,左右基本对称的情况,数据分布应该属于正常型直方图。
3 统计过程算法设计
3.1 选择控制图并画出控制图
针对频率准确度的数据特点,拟采用灵敏度较高的均值—极差控制图法来对所获得的数据进行统计分析控制图的绘制:
为了求出估计值,需要收集预备数据,共抽取m个样本(子组),每个样本的样本容量(子组大小)为n。求出每个子组的平均值、总平均值、每个子组的极差、样本平均极差
计算出上下限,先作极差R图,对状态进行判断,如果稳定就作做X均值图。如果不稳定,分析原因,改进后重复以上计算,直至稳定。A2、D3、D4、d2是常数,可查计量型控制图系数表得到
3.2 过程能力分析
一般情况而言会给定一个质量规范,即TU和TL,然后利用R和X计算CP
σ= R/d2 CP=(TU-TL)/6σ
一般情况下,总平均值与容差中心M即((TU-TL)/2不重合,所以需要计算CPK
K= CPK=(1-K)CP
3.3 统计控制方法分析
针对频率准确度的数据特点,拟采用灵敏度较高的均值—极差控制图法来对所获得的数据进行统计分析,例如:频率准确度要求为±1ppm的晶体振荡器的数据为例进行分析:
步骤1:取数据,然后将数据合理分成18个子组,每个子组的样本容量n=5,参见表1
步骤2:计算这18组样本每组的均值,例如第一组样本的均值为:
步骤3:计算各组样本的极差Ri。例如,第一组样本的极差为:
Ri=max{X1j}-min{ X1j}=0.202-(-0.012)=0.214
步骤4:计算样本总均值X与平均样本极差R
计算样本总均值X==0.145
平均样本极差R=0.257
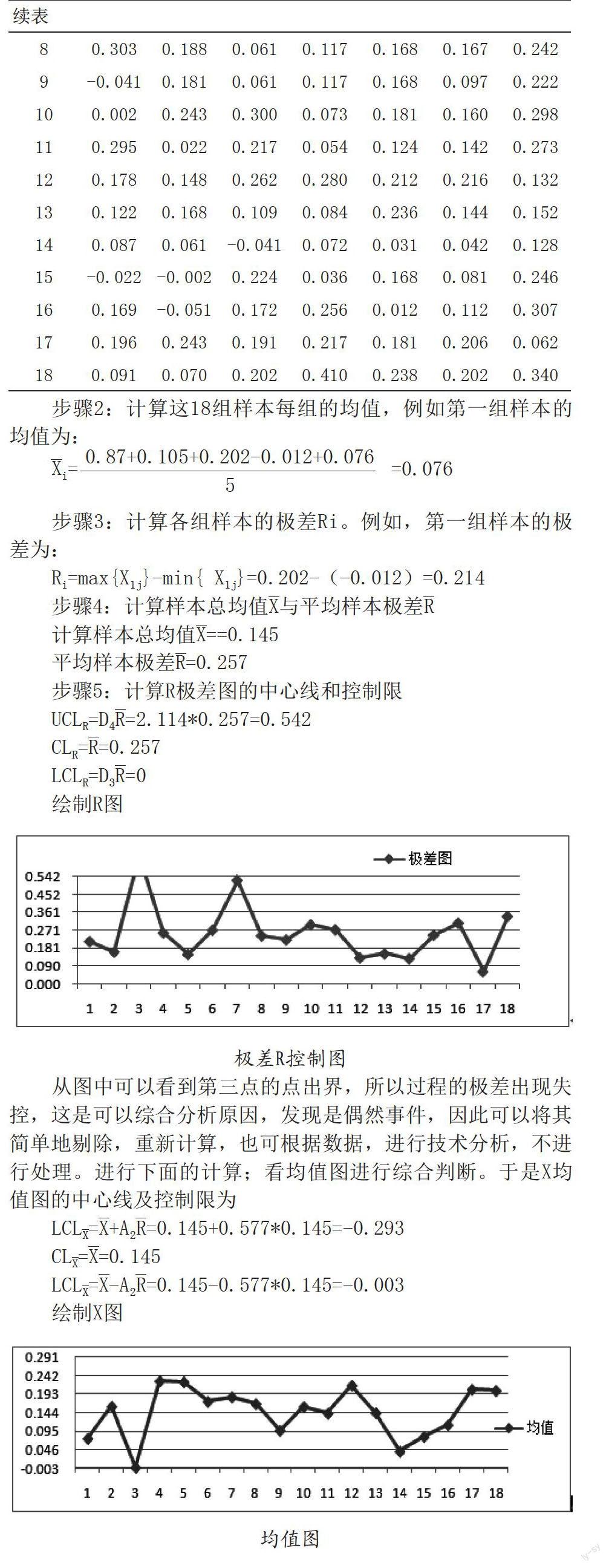
步骤5:计算R极差图的中心线和控制限
UCLR=D4R=2.114*0.257=0.542
CLR=R=0.257
LCLR=D3R=0
从图中可以看到第三点的点出界,所以过程的极差出现失控,这是可以综合分析原因,发现是偶然事件,因此可以将其简单地剔除,重新计算,也可根据数据,进行技术分析,不进行处理。进行下面的计算;看均值图进行综合判断。于是X均值图的中心线及控制限为
LCLX=X+A2R=0.145+0.577*0.145=-0.293
CLX=X=0.145
LCLX=X-A2R=0.145-0.577*0.145=-0.003
由均值图可以看出来,生产过程处于稳定状态。
步骤6,过程能力分析与规范进行比较,计算出计算CP值和CPK
对于给定的质量规范TL=-1ppm;TU=1ppm,利用然后利用R和X计算CP
一般情况下,总平均值与容差中心M即((TU-TL)/2不重合,所以需要计算CPK
K===0.145
CPK=(1-K)CP=(1-0.145)*3.058=2.614
根据均值极差图,以及计算出来的算CP值和CPK的值可以对其生产的过程能力进行综合分析,发现一般情况而言,可以依照过程能力指数CP值进行评价参考见(表5)。 表2:过程能力指数CP值的评价参考
1)CP ≥2 Ⅰ级 过程能力过高(根据情况分析)
2)1.67≤CP〈2 Ⅱ级 过程能力充分,技术管理能力很好,保持
3)1.33≤CP〈1.67 Ⅲ级 过程能力一般,技术管理能力一般,改进到Ⅱ级
4)CP〈1.33 Ⅳ级 过程能力不足,采取措施,必要时可停工
步骤7:给出结论:
因为CP=3.058和Cpk=2.614,两者都大于1.67,结合控制图,说明生产过程能力过高,然而,需要根据实际情况来分析原因,研究决定降低成本。
4 计算机在晶体振荡器频率准确度数据分析中的应用
用计算机来对数据进行统计分析,来代替手工计算,可以把大量的计算过程进行简化,如果用手工计算分析需要一天的时间,从而高效实时地对生产过程进行了控制,通过过程统计控制技术,利用一些相应的统计过程控制中的判异准则,可以及时地发现数据的异常,在产生较大损失之前及时制止,这也是利用计算机方法来进行分析运算的必要所在。
5 结语
随着计算机技术的应用和开发,质量控制也迎接来了通过软件来达到控制的目的。频率准确度是石英晶体振荡器的关键参数,在对频率准确度进行生产质量控制时,可采用均值—极差统计过程控制方法进行数据处理分析,通过绘制均值—极差控制图,以及对生产过程能力指数Cp和Cpk的计算,来判断晶体振荡器在频率准确度方面的过程加工质量方面的能力。而这一方法亦可推广到其他与频率准确度数据特点相同的其他指标的控制中,达到质量控制目的。
参考文献
[1]安炳淑.质量专业理论与实务[M].北京:中国人事出版社,2009.
[2]马林,何桢.六西格玛管理[M].北京:中国人民大学出版社,2007.
[3]赵声衡.石英晶体振荡器[M].长沙:湖南大学出版社,1997.
(作者单位:北方工业大学)
