飞机装配生产过程的仿真与工艺优化

孟 飙，闫 婧

（沈阳航空航天大学航空制造工艺数字化国防重点学科实验室，沈阳 110136）

孟 飙 副教授，工学博士，沈阳航空航天大学数字化制造工艺理论及系统研究方向负责人。近5年主持和参与国防基础科研，国防科工局“十二五”、“十三五”项目，解放军总装备部“十二五”预研10余项纵向项目，并与多家企业合作完成多项横向课题。主要研究方向为CAD/CAM、3D-CAPP、PDM/PLM等，发表学术论文30余篇，合著专著1部。

飞机制造工程是一个以装配生产为重点的复杂系统工程[1]。装配和安装是飞机制造过程中非常重要的部分，约占飞机制造总劳动量的50%～60%，与一般机械制造中装配和安装占的劳动量相比，高出了10%～15%，而飞机装配所花费时间约占全机制造周期的40%以上[2]。飞机的最终性能指标在很大程度上由飞机大部件的装配精度决定[3]。但由于飞机部件的结构复杂，制造误差控制难度较高，飞机装配过程中又会涉及到人员、工艺、质量、设备和管理等多个方面的因素，以及目前缺乏对装配制造质量、人员技术水平、生产设备状态等关键环节的有效分析方法和统计手段，过分依赖于个人经验的传统的分析方法已经难以适应日益复杂的企业制造需求。

飞机的部件装配车间一般有很多装配生产线，并设有许多个生产班组。在装配过程中，不同的班组需要使用各种工装、工具和设备。不同的生产线需要完成不同部件的装配，每种部件的装配往往包含上百道工序，其工艺流程相似。由于航空产品直接面向需求，以客户为导向，航空制造企业在产品需求、交货时间、产品质量等方面都必须满足客户的需求。因此，由于各个生产线间存在着资源共享、资源竞争等现象，使得对装配时间的优化变得更加复杂。为了提高飞机部件装配生产线的装配效率，需要对整个飞机部件装配线进行建模，为飞机部件装配线的分析和优化提供依据。

装配资源的配置

飞机装配工程是一项非常复杂的系统工程，涉及飞机设计、工艺计划、零件生产和部件装配全过程[4]。飞机装配具有以下特点：（1）产品结构复杂、生产周期较长；（2）生产工艺复杂，过程离散且多变；（3）多品种、小批量、多研发、少批产；（4）生产管理与生产现场数据量庞大、多变； （5）难以建立产品化的信息化解决方案[5]。

通过对飞机大部件装配过程中各种资源分类和分析，建立11个模块解决飞机大部件装配过程中的建模和配置优化，即工序详细调度、资源分配和状态管理、生产单元分配、文档控制、产品跟踪和产品清单管理、性能分析、人力资源管理、过程管理、质量管理、数据采集、维护管理。

装配工艺过程模拟仿真

由于Petri网模型具有直观、形象、易于理解、有成熟的数学分析方法等特点，根据飞机典型大部件装配的特点，建立装配工艺过程的仿真模型。考虑到生产线生产过程中的工艺约束、资源约束、工时信息，提出一种基于时延Petri网TdPN(timed Petri net)装配模型构建方法。通过对TdPN模型的分析，进行生产线的优化实现按时交付产品。

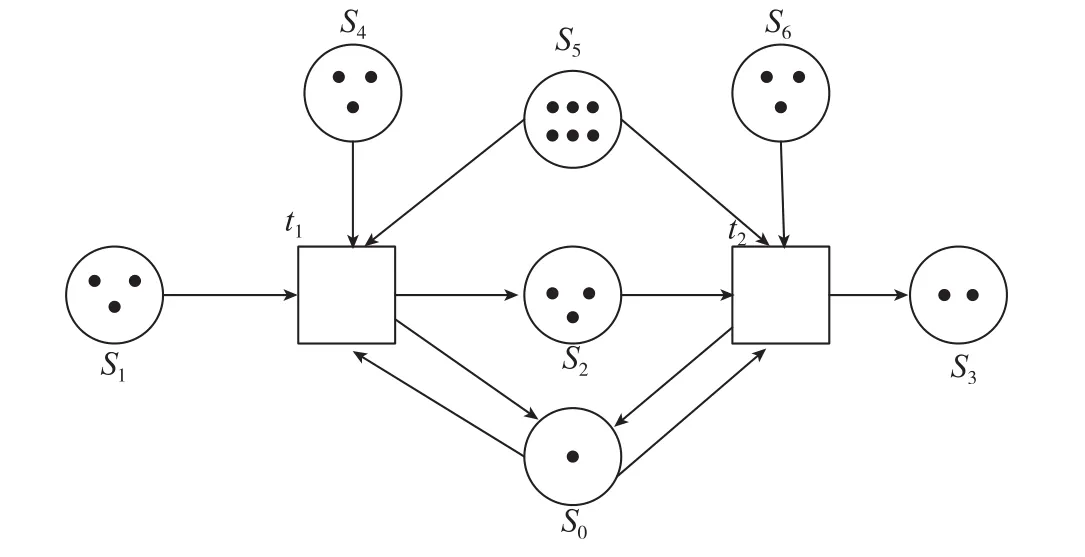
图1 一个装配线片段Fig.1 A piece of the assembly line

1 基于Petri网的装配生产线建模

装配生产线是典型的物质资源流动，半成品在流水线上移动，在每个生产环节组装上对应的部件，一直到生成最终的产品。首先对一个装配线片段进行建模，如图1所示。图1中方框“□”和圆圈“○”分别代表一个生产过程环节T_元素和一种资源S_元素，其中黑点个数表示该种资源的数量；S1、S2、S3为装配过程中的装配件；S4、S5、S6表示零件；S0表示工具；t1、t2表示装配过程。

图1中箭头的方向代表的是资源装配的方向，箭头上的数字则代表装配所需要的该种资源的数量，称为弧上的权，默认为1[6]。装配工序t1是用两个零件S5把1个部件S4装配到S1上产生1个新的半成品S2。此时工具S0只有1个，即t1和t2在竞争共享的资源S0，所以工序t1和t2不能同时装配。Petri网中把这种竞争关系称为冲突，实际装配线生产中经常会遇到类似的本应该避免出现的问题。如该模型中t1和t2处于平等竞争的地位，而装配线上并没有规定具体的占用规则，因此容易出现t1和t2中某1个工序被连续占用多次，而另外1个工序没有机会使用的情况，所以又把这种资源冲突称为不确定冲突，如果仅考虑工具S0的使用情况，这种不确定性会导致装配生产线出现资源被其中的1个工序无限占用，另1个工序处于“饿死”状态。但如果库所S2上标明了容量K=10，表示工序t1可以连续发生10次，当S2的容量超过10时，就会停止工序t1，之后工序t2便有机会使用工具S0，这样模型就不会出现饥饿现象。在该模型中，每个S_元素都应该有确定的容量，但是为了保证图形简洁，只对需要特别需要的库所规定容量。传统上凡不明确给出的容量均可以默认为无穷[7]。

在实际生产中，装配生产线上应有解决资源冲突的机制，就是增加1个资源，让装配工序t1和装配工序t2各有专用资源，这种资源竞争冲突自然也就消失了，这时资源已经不是影响装配工序t1和t2能否发生的因素，所以可以从模型中删除掉S0级相关箭头，得到这种无竞争的装配生产线的网表示。事实上，装配生产线是少不了工人的，但是因为一般装配生产线的每个环节都有专人负责，就像专用工具一样，不是约束性因素，不必明确描述。

2 基于TdPN对部件装配生产线建模

飞机典型部件装配过程一般要由组合件装配、段件装配和部件装配3个阶段组成。根据飞机部件装配过程中的3个阶段，结合飞机部件装配线特点，基于TdPN模型建立部件生产线模型的方法和步骤，如图2所示。其中，库所用来表示各个装配阶段所需要的资源，可分为3种:（1）pn（n=1，2，3，…）是该生产线所有组件装配的零件库所，表示参加组件装配的零件的状态；（2）sun（n=1，2，3，…）是该生产线所有段件装配的零件库所，表示进行段件装配的零件的状态；（3）un（n=1，2，3，…）是该生产线部件装配的零件库所，表示进行部件装配的零件的状态。

装配顺序图中变迁表示装配过程中，这里没有表示出进行该装配需要的时间，即用瞬时变迁来表示，可分为 3 种：（1）tpn（n=1，2，3，…）表示该生产线所有组件从零件到组件的装配过程；（2）tsun（n=1，2，3，…）表示该生产线所有段件从组件到段件的装配过程；（3）tun（n=1，2，3，…）表示该生产线从段件到最终部件的装配过程。考虑到装配过程中还会涉及到相关设备和人员，用ei（n=1，2，3，…）表示装配过程中的各种设备；wi（n=1，2，3，…）表示装配过程中的人员（可以表示1个班组或1个人员）。人员和设备在装配过程中属于不会被消耗的资源。为了对装配生产线进行基于时间的优化，需要对各工序进行扩展，加入每个工序需要的设备、人员和时间，如图3所示。

装配工艺过程工艺优化

1 基于资源的装配线优化

飞机部件的构造复杂，需要装配的零件数量众多，装配工作量巨大。对装配线进行基于资源的优化时，人力资源和设备资源在装备过程不会被消耗，进行资源优化时需要对生产线Petri网系统进行重新构造。1个m维的非负整数型向量可以用Petri网的1个标识来表示，那么通过矩阵就可以表示Petri网的结构；这样就可以用线性代数的方法对Petri网的性质进行分析[8]。因此，部件装配线Petri网模型也可以用1个矩阵来表示，并用线性代数的方法对部件装配线进行分析。

设∑=(S,T;F,M)为1个Petri网，其中S={s1,s2,…,sm}，T={t1, t2,…,tn}；则Petri网∑的结构(S,T;F)可以用A=[aij]n×m来表示，其中，

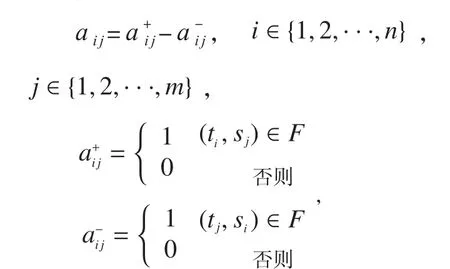
称A为∑的关联矩阵。

根据上述定义，纯网中的任何1个变迁和任何1个库所之间最多只可能有1个弧，绝不会出现a+ij和aij相互抵消的情况。或者说，关联矩阵只有与纯网结构之间才能存在一一对应的关系。因此，使用关联矩阵对Petri网模型进行分析时，必须要求所分析的Petri网为纯网。

为方便分析，引入两个n×m的矩阵，并分别称它们为∑的输出矩阵和输入矩阵。分别用标识矩阵A、A+和A-的第i行的行向量，分别用标识矩阵A、A+和A-的第j列的列向量。∑的标识M仍用m维非负向量来表示。

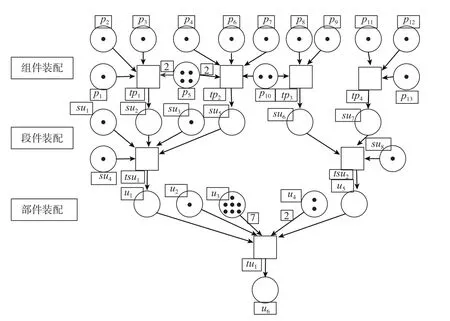
图2 用基本Petri网建立的部件装配线模型图Fig.2 Parts assembly line model diagram set up by using the basic Petri net

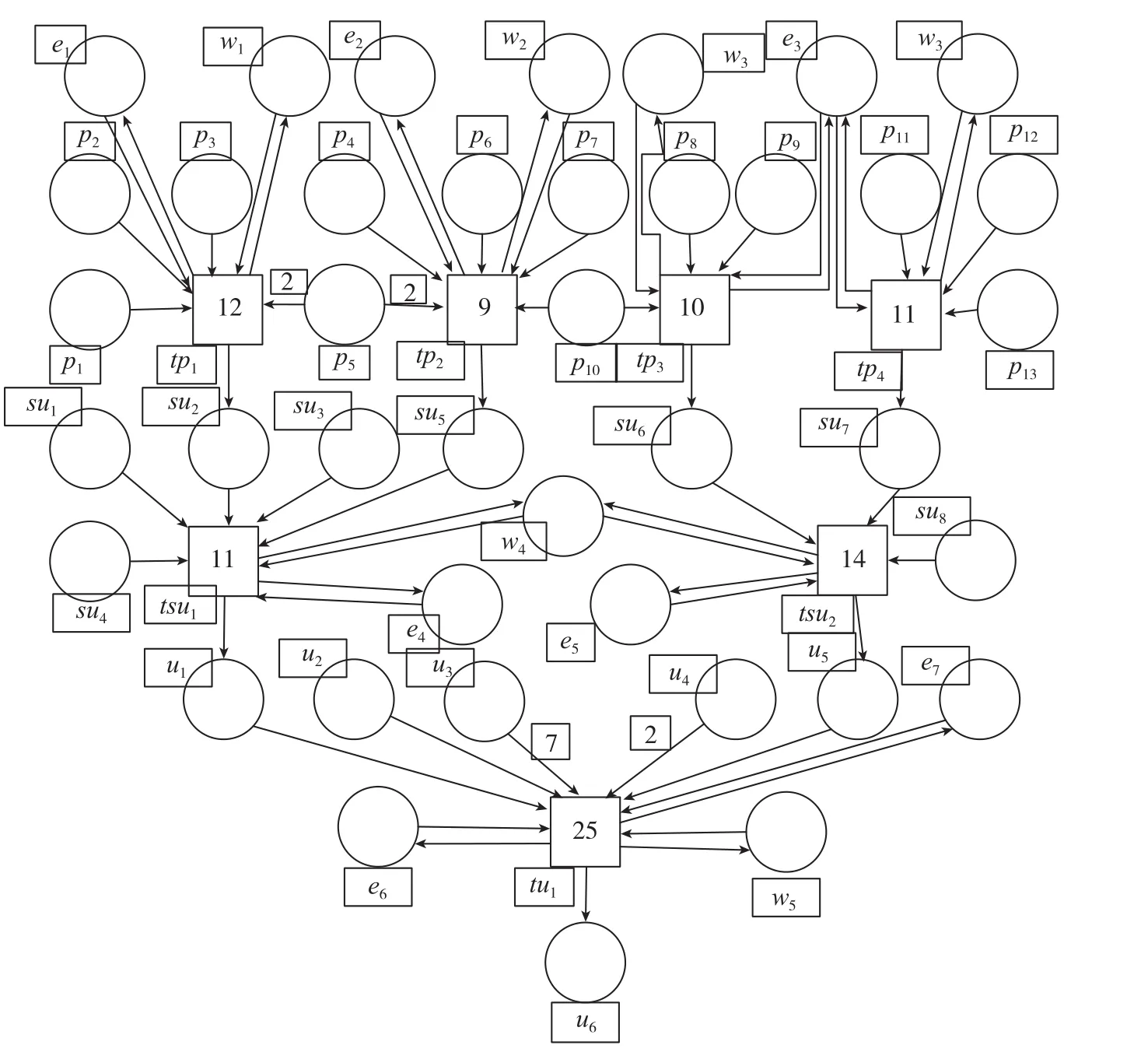
图3 加入设备、人员、时间的Petri网模型Fig.3 Petri net model with equipment,personnel and time

根据上述要求通过下列步骤完成对装配生产线Petri网系统的重新构造，使装配生产线Petri网系统成为1个纯网，通过关系矩阵完成对基于资源的优化。

初始标识M0在这里表示各种资源的准备情况。不同的初始标识表示不同的资源准备状态。M0表示整个部件装配线初始运行时的初始状态，不同M0表示装配初始运行时不同的状态，M'是完成部件装配的状态，具体的状态为装配线的最终产品，表示装配完成，表达式是M'=[0 0… 1]。通过计算和分析可得到从M0到M'的可达性变迁顺序。判断可达性的具体计算方法为：对于M'如果存在非负向量X，使得M'=M0+ATX，M'从M0可达。因此也说明对于初始状态M0的资源装备状态可以完成部件的装配。

对于不存在非负向量X的情况，由于此时没有非负向量X使得M'=M0+ATX，则说明初始资源准备状态M0无法满足完成最终的部件要求，对于这种情况需要使用M'=M+(Ai*)T求出该M0对应的M'，计算出可以进行装配的工序，先进行这些可以装配的工序，等资源准备充足后在M'的基础上重新定义新的M0，一直到存在非负向量X，使得M'=M0+ATX，M'可从M0可达。

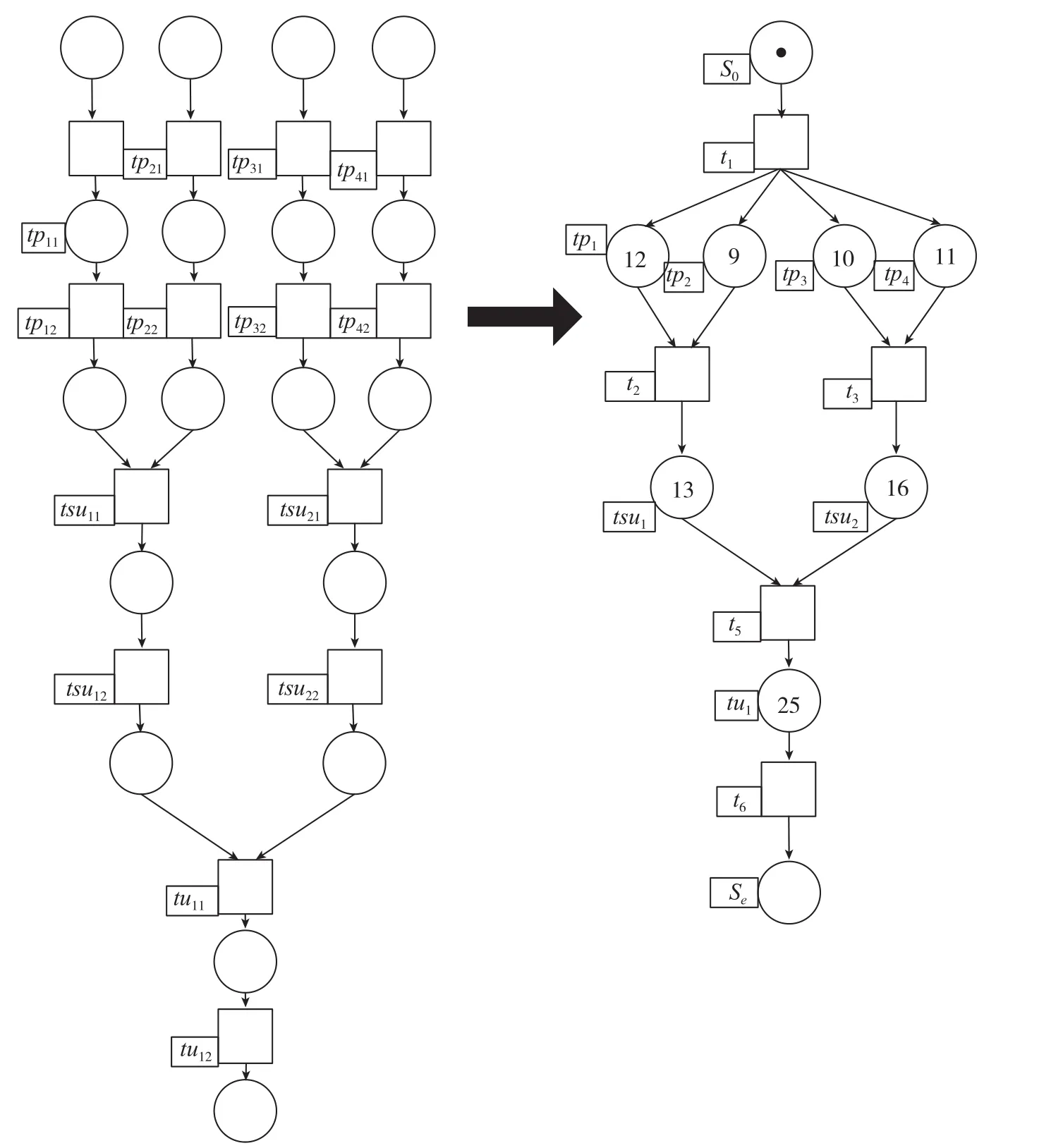
图4 构建时延Petri网Fig.4 Building the timed Petri net

2 基于时间的装配线优化

飞机装配生产线时间优化需要求解的量主要包括：（1）各个装配工序的最早开工时间；（2）完成整个部件装配需要的最短时间；（3）为保证整个部件装配用最短时间完成而规定的各个装配工序的最晚必须开工时间。在此基础上优化装配顺序，制定出为保证整个部件装配用最短时间装配完成的合理装配方案。通过对重新构建后的Petri网模型∑和∑的可达标识图RG(∑)分析来求解。

时延Petri网的定义同Petri网排斥全局时钟的原义相悖，同时也与变迁发生的瞬间性原理相悖[9]。因此需要用两个变迁和1个库所的连接表示一道工序，在保证不会使各工序之间的衔接关系发生改变的前提下，把某些权为零的库所消除，将该库所连接的两个工序的完工变迁和开工变迁合并成1个变迁，这样就完成了对整个装配的Petri网模型的重新构建，如图4所示。那些为保证工序间的衔接关系而必须保留的权为零的库所代表虚工序[10]。这样便可构造出一种库所含有时间因素的Petri网。因为对各库所赋予的时间是一个确定的非负实数，即各库所的权值是一个确定的非负实数，可认为它们是由时延Petri网经过改造而得到的，其中用对库所赋予非负实数值来代替对变迁赋予非负实数值[11]。

对于部件的装配，根据部件装配的Petri网模型，从S0开始逐个向装配的下一步进行，可以求出各个装配工序单元的最早可能开工时间E(Si)；求出部件装配的最后一道工序的E(Se)，就得到了完成整个部件装配所需要的最短时间；然后从装配工序Se开始，逐个追溯，就可以求出保证整个部件装配用时完成的各装配工序最晚必须开工时间L(Si)。

对于一个肯定型工程问题的Petri网模型，在该模型中必存在一条从S0到Se的有向路，对该有向路上的每个库所Si，都有L(Si)=E(Si)。满足L(Si)=E(Si)的有向路就是该装配线的主工序线。因为对于这种有向路上的每一个装配工序而言，最晚开始装配时间都等于最早可能开始装配时间，所以若装配过程中某道装配工序不能按规定时间完成装配，就会使后续装配工序的开始装配时间推迟，使得整项工程不能在最短时间TE内完成。可达性是Petri网具有的最基本的动态性质，其余的性质都需要通过可达性来进行定义，可达标识图是Petri网模型的非常重要的分析方法，因为有界Petri网模型的可达标识集是一个有限集，所以可以用作为顶点集，用标识之间的直接可达关系弧集形成一个有向图来进一步分析[12]。通过一个可达标识图可以分析这个网系统的状态变化情况以及变迁发生序列的情况，这样就得到了该Petri网系统的相关性质。

在进行分析之前需要求出装配线Petri网模型的可达标识图RG(∑)，如图5所示。

从M0到Mt的各条有向路组成了∑的可达标识图RMG(∑)，它是一个不存在有向回路的有向图，其中一部分有向路可能会有一些公共边和公共结点。每条有向路的长度都等于|T|；在每条有向路上，∑中的每个变迁都刚好是一条边的旁标[13]。一条这样的有向路代表装配的可能装配方案，但并不是每一种装配方案都能保证整个装配用TE时间完成,即成为合理的施工方案。

通过下面的方法，用可达标识图RMG(∑)来确定部件装配生产线的合理装配方案。

对 于M∈R(M0)，用E(M)表示标识M的最早可能出现时间，用L(M)表示保证整项工程用TE，标识M存在的最晚时间。

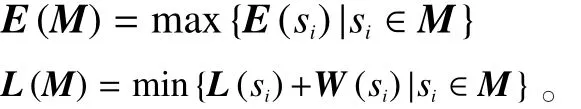
如果一种装配顺序M出现在一个合理装配方案中，则该装配顺序出现的区间 [τ1(M),τ2(M)]必须满足 :

E(M)≤ τ1(M) ＜ τ2(M)≤L(M)。

从图6可看出装配的正确路径为:M0→M1→M3→M4→M5→M6。结点M2出现E(Mi)＞L(Mi)的情况，这种情况是部件装配过程中不应该出现的装配状态。

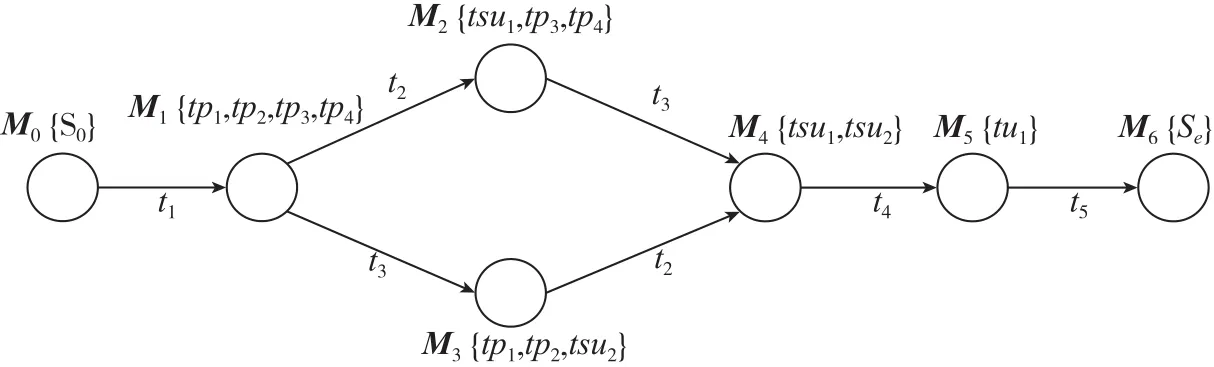
图5 部件装配线的可达标识图Fig.5 Reachable logo figure of a part-assembly line

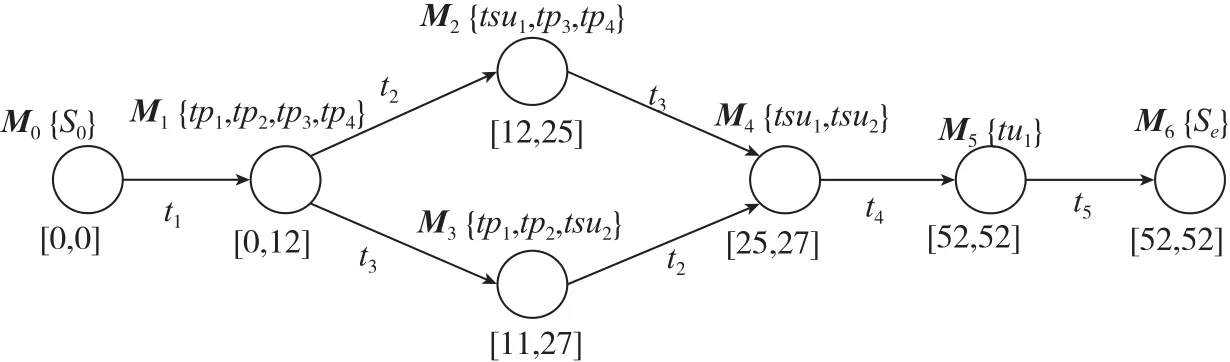
图6 加入各标识合理存在时间的部件装配线可达标识图Fig.6 Reachable logo figure of a part-assembly line with reasonable existence time of each logo

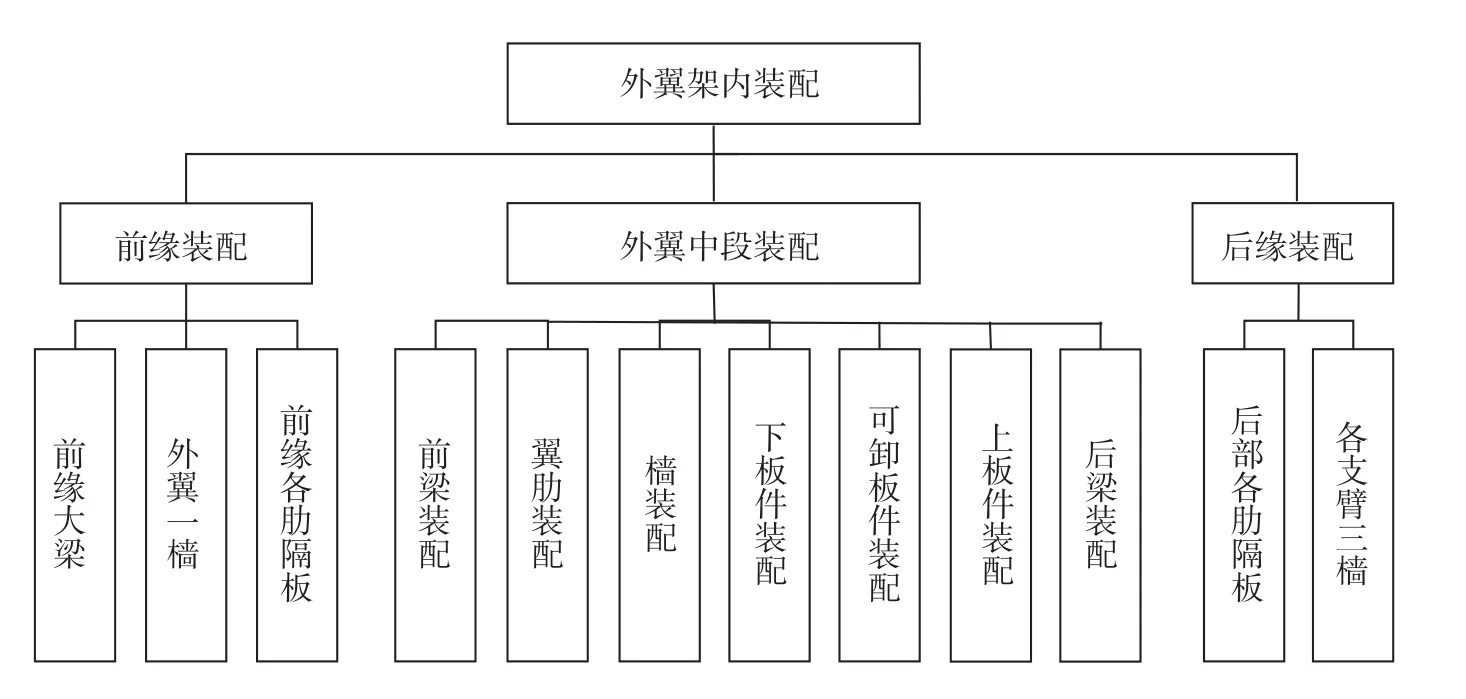
图7 外翼装配架构图Fig.7 Outside wing assembly architecture diagram

实例验证

本文根据实际部件装配过程建立某型号飞机外翼的装配过程模型，结合模型对此部件的装配过程进行仿真。依据确定的基于资源和时间的部件装配生产线优化方法，以生产线平衡为基础进行优化，并对优化结果进行仿真，从而验证了建模仿真和优化算法的可行性。

1 基于资源约束的外翼装配线优化

该型号飞机外翼装配包括前缘装配、外翼中段装配和后缘装配3个装配站，如图7所示。

根据前文所述的装配工艺过程，依据本文中提出的理论，基于基本Petri网建立三级装配模型。首先分三级对外翼装配模型中的各个参数进行定义，如表1所示。

根据基于资源的装配线优化和基于时间的装配线优化两节中的步骤建立人员和装备充足情况下外翼装配生产线的Petri网系统模型，如图8所示。

图 8 中pn（n=1，2，3，…）是外翼装配生产线所有组件装配的零件库所，主要用来表示组件装配过程中所有需要的资源，箭头表示进行组件装配时所需要的资源的数量，没有写出来表示装配的时候需要的数量为1。

对于外翼装配生产线假设初始状态为：

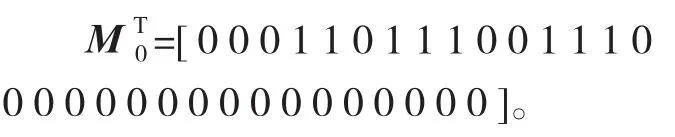
对于此M0状态，因为不存在能够使得M'=M0+ATX的非负向量X，此种状态下外翼装配生产线不能装配出外翼，但是可以先进行资源充足的装配工序的装配，在这种情况下，初始状态M0为前缘装配站中隔板装配组件装配需要的零件准备充分，满足装配需要；外翼中段装配中前梁装配、上板件装配、下板件装配、可卸板件装配、翼肋装配各个组件装配需要的零件准备充分，满足装配需要；后缘装配中后缘各肋装配组件装配需要的零件准备充分，满足装配需要。装配过程的矩阵的表达式为M1=M0+(A4*)T+(A5*)T+(A7*)T+(A8*)T+(A9*)T+(A11*)T+(A13*)T，通过矩阵变换得到新的外翼装配状态M1。

在M1状态下如果没有进行新的资源准备的情况下，外翼装配只有变迁后梁装配工序、樯装配工序处于发生状态，此种情况下为保证装配正常进行，可以先进行后梁装配工序和樯装配工序的装配，装配过程的矩阵的表达式为M2=M1+(A6*)T+(A10*)T，通过矩阵变换得到新的外翼装配状态M2。

在M2状态下如果没有进行新的资源准备的情况下，只有变迁外翼中段装配工序满足变迁发生条件，其他装配工序因为资源不足而无法进行装配，如果此时缺少的零件不能得到满足，则只能进行外翼终端装配工序。如果此时有缺少的零件加入，M2的状态就发生了变化，满足条件的工序就可以继续进行装配，假设此时在本次外翼装配M0状态缺少的零件得到满足，此时M2的状态变更为，变更后的M2状态满足存在非负向量X，使得M'=M0+ATX，M'从M2可达，即M2状态下的资源准备状态可以完成外翼的装配。M0状态缺少的零件得到满足，符合发生条件的装配工序发生了变化，此时变迁前缘大梁装配工序、外翼一樯装配工序、前缘各肋装配工序、支臂装配工序、三樯装配工序、变迁外翼中段装配工序满足变迁发生条件。装配过程矩阵表达式为M3=M2+(A1*)T+(A2*)T+(A3*)T+(A14*)T+(A15*)T+(A17*)T，通过矩阵变换得到新的外翼装配状态M3。

在M3状态下，变迁前缘装配工序、后缘装配工序符合变迁发生条件，装配过程的矩阵表达式为M4=M3+(A16*)T+(A18*)T，通过矩阵变换得到新的外翼装配状态M4。在M4状态下，变迁外翼装配工序满足变迁发生条件，变迁发生后进入M5状态。，此刻表示外翼装配生产线的产品外翼完成装配，重新进入下一个装配过程。上述过程完成对外翼装配线基于资源的优化，通过矩阵计算，可以方便得出各种资源准备情况下1个工序的装配顺序，保证外翼装配线的高效运行。

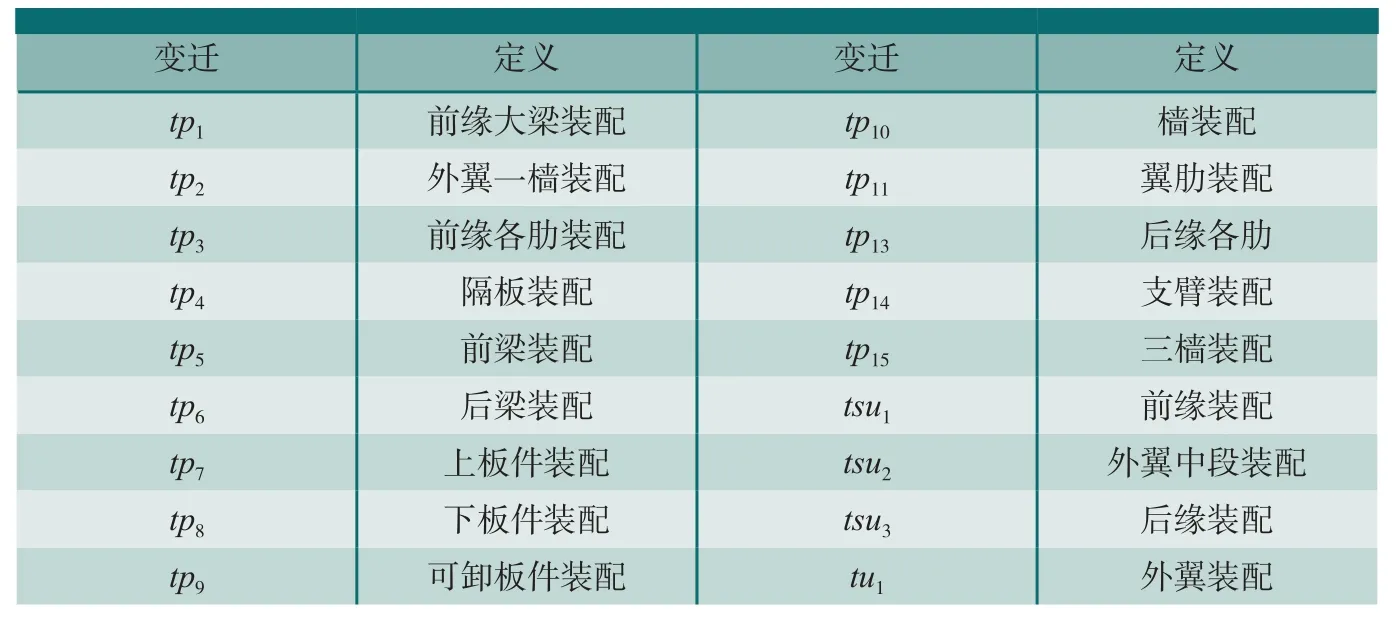
表1 部件装配工序参数定义

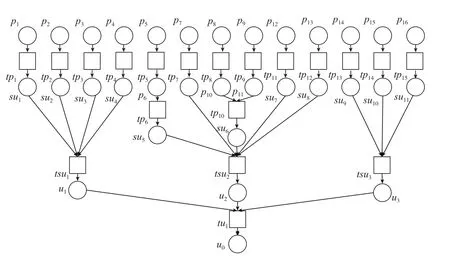
图8 人员和装备充足时外翼装配生产线Petri网系统模型Fig.8 Petri net model of the system with plenty of personnel and equipment

2 基于时间约束的外翼装配线优化

外翼装配线可以划分成若干道工序，外翼装配过程中的每一个工序所需要的工时都是一个确定值，外翼装配线是一个肯定型TdPN模型。前面已经根据装配中各工序之间的衔接关系和工序的工时，构造出外翼线的Petri网模型。现在对该型号飞机外翼装配生产线进行基于TdPN的模拟仿真，如图9、10所示。

通过对该型号飞机外翼装配过程进行分析，根据基于时间的装配线优化所述方法，可得到外翼装配线TdPN模型各个库所si的E(si)和L(si)，如表 2所示。

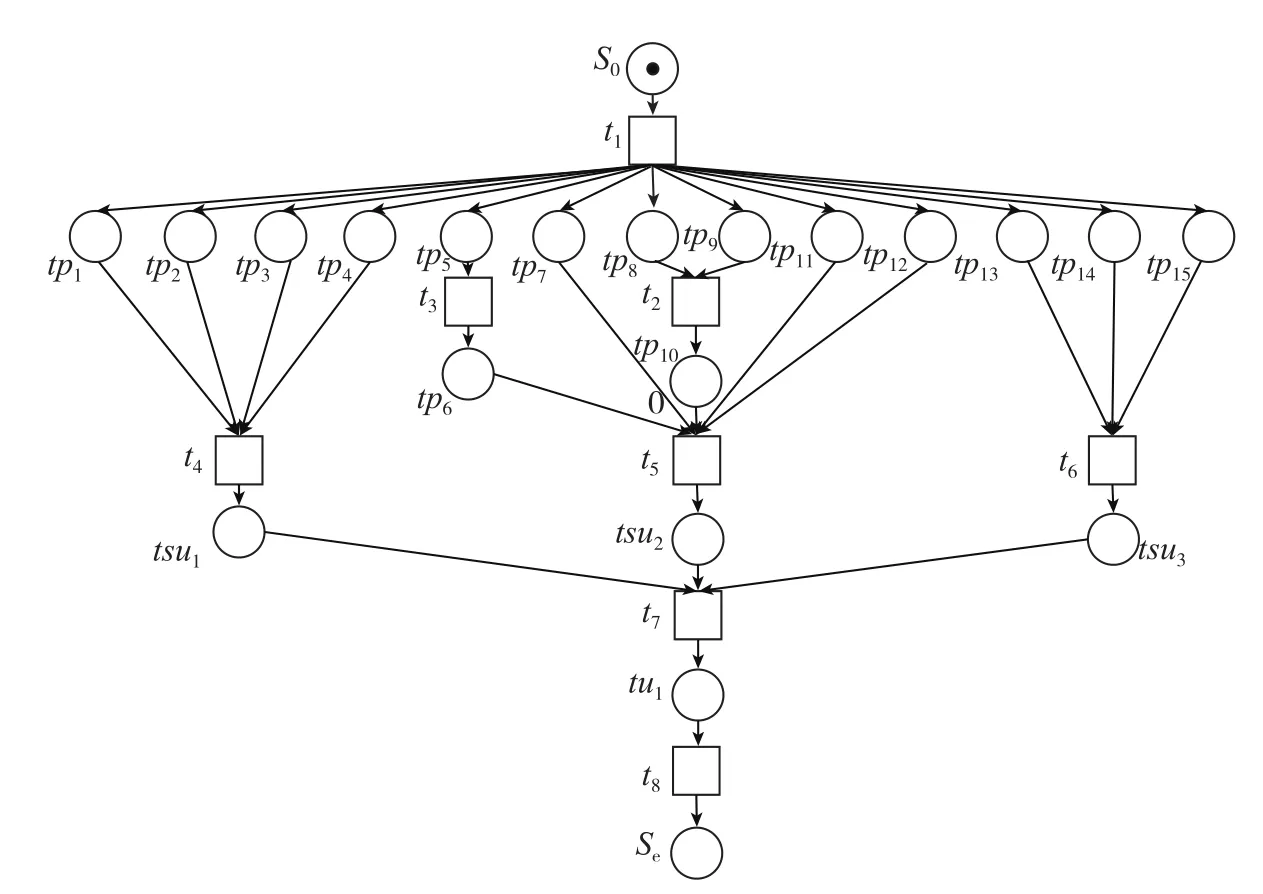
图9 外翼装配线TdPN模型Fig.9 Outside wing assembly line TdPN model

图10 装配仿真优化系统Fig.10 Assembly simulation optimization system

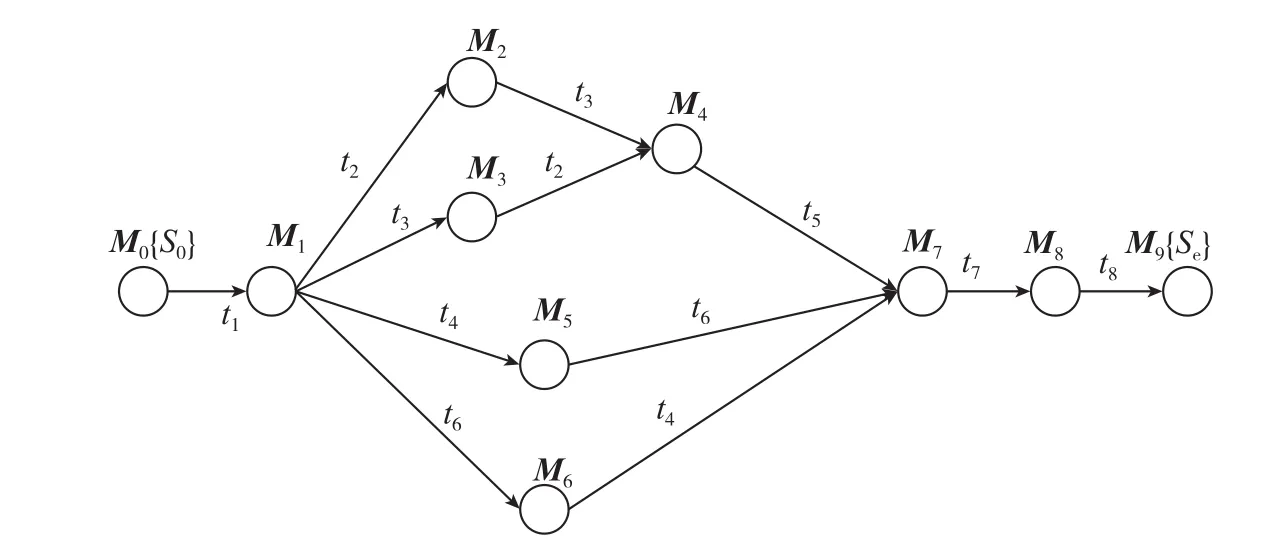
图11 外翼装配线可达标识图Fig.11 Reachable logo figure of outside wing assembly line

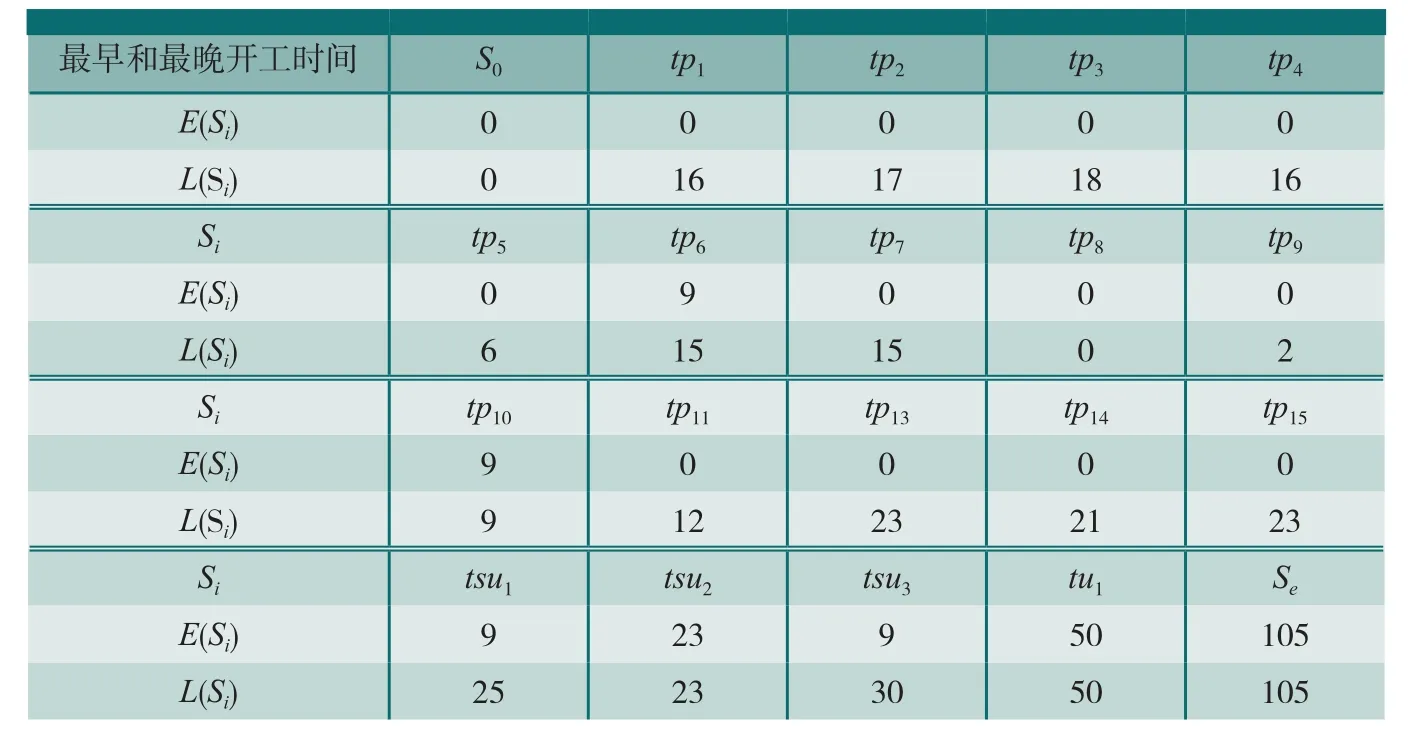
表2 外翼各工序最早开工时间及最晚开工时间

根据图9和表2可以得出，整个外翼装配所需要的最短装配时间为TE=E(se)=105。外翼装配线主装配工序线上的每一个库所S都有E(s)=L(s)，s0和se在这里分别代表装配开始和装配结束的两个虚装配工序，所以整个装配线TdPN网模型的实际工序线为

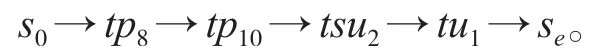
对于外翼装配线装配主工序线的每一个装配工序，最晚开始装配时间都等于最早开工时间，主装配工序线上的每一个工序都必须按时装配，如果有一个外翼装配线中的装配工序不能按预定时间完成，就会使后续装配的开工时间推迟，从而使整个外翼装配不能按最短时间完成装配。

因为通过L(Si)=E(Si)确定的外翼装配主工序线并不是唯一的，所以需要通过外翼装配的Petri网模型的可达标识图RG(∑)来确定外翼装配的合理装配方案。根据外翼装配的Petri网模型构造出可达标识图，如图11所示。

通过分析发现，有出现E(Mi)＞L(Mi)的情况。这种情况是装配过程中不应该出现的装配状态，从图11中可以看出装配的正确路径是：M0→M1→M2→M4→M7→M8→M9，通过上述过程求解，求出了装配主工序，各个工序的最晚开工时间和最早开工时间，通过这些数据可以完成对外翼装配生产线各个装配环节进行优化。

结束语

随着近年来信息化、数字化建设的发展，飞机数字化制造有了强有力的硬件支撑。通过运用Petri网模型对装配生产线进行建模，将实际生产中的装配过程抽象成数学模型进行分析，突破了传统分析手段的局限性，完成了由离散的数据分析与处理环境向集成化、综合化的方向过渡，实现数据管理、关联分析、信息发现、统计展示等功能的集成，实现数据共享性和同源性；通过建立综合评价模型完成评价指标的统计与计算，进而实现人员属性、设备状态、装配质量与装配周期的多层次综合分析与评估，为制订有针对性的工艺优化措施提供数据与信息支持。

[1]苟坤.面向飞机装配过程的质量管控系统研究与应用[D].武汉:华中科技大学,2012.

GOU Kun.Research and application of quality management system for airplane assembly[D].Wuhan: Huazhong University of Science and Technology,2012.

[2]燕宜军.基于AO的飞机装配架次管理系统的研究与开发[D].南京:南京航空航天大学,2007.

YAN Yijun.Research and development of aircraft assembly shipset management system based on AO[D].Nanjing: Nanjing University of Aeronautics and Astronautics,2007.

[3]LSAT M,KANDEL A.Data mining for process and quality control in the semiconductor industry[J].Data Mining for Design and Manufacturing,2001,13(4):207-234.

[4]范玉青.飞机数字化装配技术综述—飞机制造的一次革命性变革[J].航空制造技术,2006(10):42-48.

FAN Yuqing.Aircraft digital assembly technology reviewed revolutionary change of aircraft manufacturing[J].Aeronautical Manufacturing Technology,2006(10):42-48.

[5]KUSIA A.Rough set theory: a data mining tool for semiconductor manufacturing[J].IEEE Transactions on Electronics Packaging Manufacturing,2001,24(1):44-55.

[6]高峰,孙培良.装配生产线调度控制模型算法研究[J].武汉工业学院学报,2002(3):49-51,54.

GAO Feng,SUN Peiliang.Scheduling strategy and control methods for the assembly process[J].Journal of Wuhan Polytechnic University,2002(3):49-51,54.

[7]DABBS R M,CHEN H N.Mining semiconductor manufacturing data for productivity improvementan integrated relational database approach[J].Computers in Industry,2001,45(1):29-44.

[8]高茜.活的单支Petri网的可达性判定方法及改进的可覆盖性树的构造算法[D].济南:山东大学,2008.

GAO Qian.A method for reachability decision of live single branch Petri-net and an algorithm for construction of improved coverability tree[D].Jinan:Shandong University,2008.

[9]肖军,邓海鸿,周春贵,等.基于Petri网的工作流过程模型及资源分布分析[J].计算机应用研究,2009(7):2593-2597.

XIAO Jun,DENG Haihong,ZHOU Chungui,et al.Workflow process model and resource distribution analysis based on Petri net[J].Application Research of Computers,2009(7):2593-2597.

[10]王青,温李庆,李江雄,等.基于Petri网的飞机总装配生产线建模及优化方法[J].浙江大学学报（工学版）,2015(7):1224-1231.

WANG Qing,WEN Liqing,LI Jiangxiong,et al.Modeling and optimization for aircraft final assembly line based on Petri net[J].Journal of Zhejiang University(Engineering Science),2015(7):1224-1231.

[11]常显斌.研发合作知识创新的资源分配研究[D].青岛:中国海洋大学,2010.

CHANG Xianbin.Research on resources allocation of cooperative knowledge creation for R&D[D].Qingdao: Ocean University of China,2010.

[12]马志奇,杨宏文,胡卫东,等.一种新的基于邻接矩阵的拓扑排序算法[J].计算机应用,2007(9):2307-2309.

MA Zhiqi,YANG Hongwen,HU Weidong,et al.New topological sort algorithm based on adjacency matrix[J].Journal of Computer Applications,2007(9):2307-2309.

[13]宋洪军.基于中间件和虚拟现实的异构机器人作业系统研究[D].济南:山东大学,2008.

SONG Hongjun.Study of middleware and virtual reality based heterogeneous robot job system[D].Jinan: Shandong University,2008.