基于灰色关联度和TOPSIS的输电线路防污方案决策研究

帅海燕

( 武汉交通职业学院，湖北 武汉 430065)



基于灰色关联度和TOPSIS的输电线路防污方案决策研究

帅海燕

( 武汉交通职业学院，湖北 武汉 430065)

摘要：为进一步提高电力系统的供电可靠性，将灰色关联度和理想解法 (TOPSIS)应用到输电线路防污方案决策中，构建基于灰色关联度和TOPSIS的防污决策模型.通过综合分析，在兼顾安全性和经济性的基础上，选用“防污所需技术水平”、“防污风险”、“防污对生产影响”、“防污综合费用”、“防污效果”5个决策指标对WSCC-9系统中的污闪中风险输电线路防污方案的决策过程进行分析,并具体探讨该决策方法在防污决策中的应用,与已有方案对比结果显示该方法更有优势.

关键词：输电线路；防污方案决策；灰色关联度；理想解法

0引言

由于我国电网发生多次各种规模的污闪事故，给国民经济造成了巨大的损失.为提高电力系统的供电可靠性，电力工作者为防污闪进行了大量的研究[1-5].文献[1]中概述了从建国初期到2005年我国发生污闪后所采取的防污措施，并提出今后防污的方向.文献[2-5]中针对不同地区污闪事件进行分析，并提出了相应的处理办法.从总体上看这些文献都只在污闪事故发生后，对事故发生的原因进行分析并提出相应的改进措施，体现出明显的被动性、机械性和滞后性；另外文献中的论断均出自定性分析的结果，因此缺乏一定的科学性.文献[6]中利用模糊C均值分类法依据风险评估的结果将输电线路分成高、中、低风险3大类线路，在恶劣天气到来之前，相应线路盐密已超过规定值时，直接将这3大类线路对应3个防污方案.尽管这种防污方案的决策优于传统的方法，但防污方案的决策涉及多个因素，是一个多指标决策过程，因此，简单地对不同污闪风险的输电线路直接利用模糊C均值分类法进行防污决策显得过于草率，故应引入一种多指标决策法来优选方案.理想解法(TOPSIS)作为一种经典而有效的多指标决策法，已广泛应用于项目评价、投资决策、方案选优等领域[7-8].但在防污方案决策过程中，因受到统计数据量不足，人为因素，数据波动较大且没有典型的分布规律，指标之间数量关系的不确定性等因素的影响，使其带有明显的“灰色”特征.为进一步完善上述防污方案的决策，本文中以WSCC-9系统为例在文献[6]和[9]研究成果的基础上，将基于灰色关联度和理想解法(TOPSIS)的决策方法引入到对有限的防污方案的综合评价中.

1输电线路防污方案决策的思路

首先利用文献[9]中预测方法预测WSCC-9系统每条线路的实时盐密时并与该线路污秽等级所对应的值相比较，判断线路盐密值是否越限；其次，将盐密判断结果与文献[6]中输电线路风险分类结果(高风险线路、中风险线路和低风险线路)相结合，若线路盐密没有越限，则实施“不安排防污”方案；若已越限，高风险线路则实施“提前防污”；低风险的线路实施“暂缓防污”；而中风险线路则利用灰色关联度和理想解法在3种方案(暂缓防污、针对性防污、优先防污)中进行决策判断，以确保防污措施的安全性和经济性.这里的防污方案决策是指大雾、凝露或毛毛雨的天气到来之前，对风险指标不同的线路所应采取的措施，见图1.

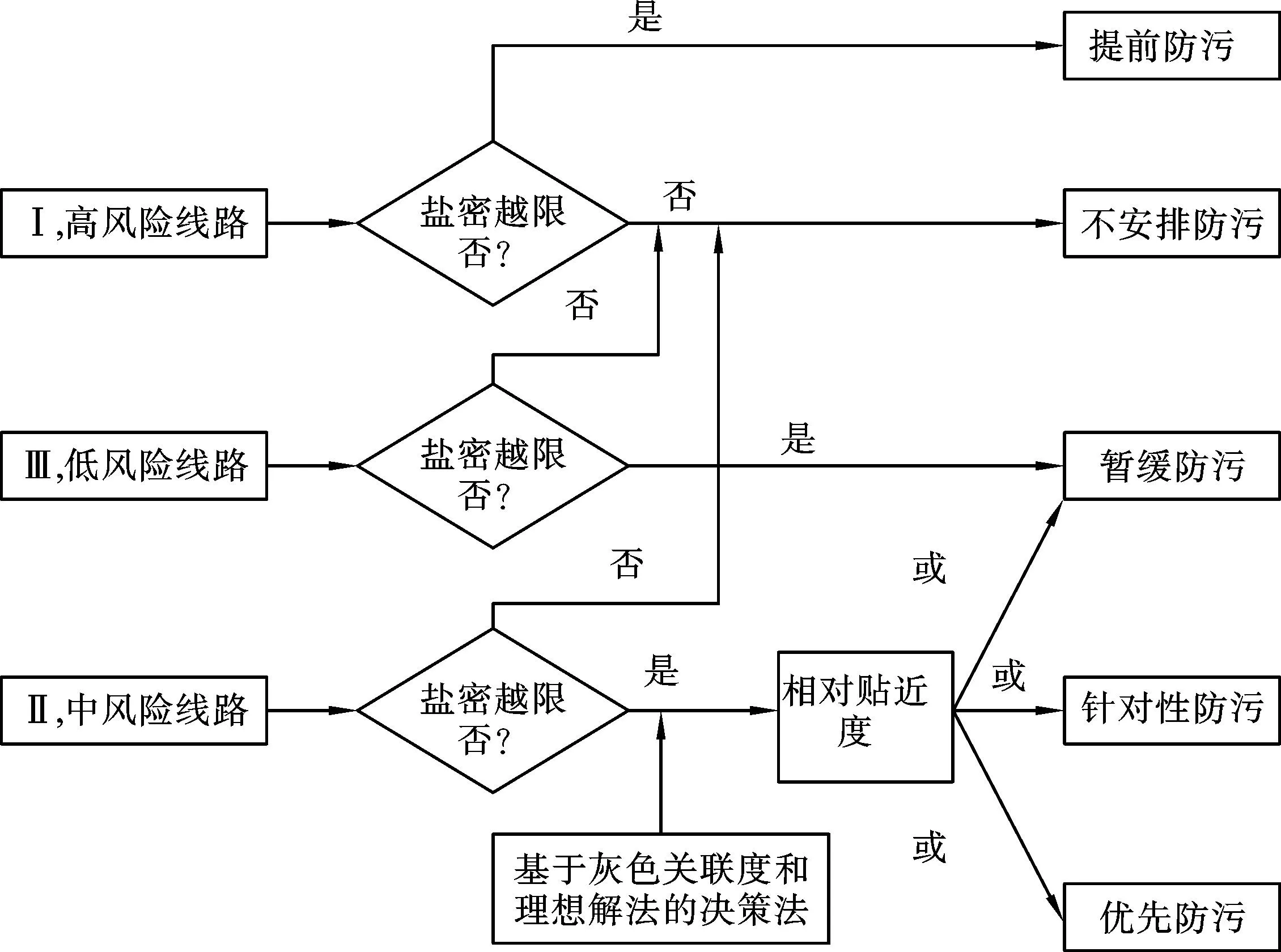
图1　输电线路防污方案决策示意

2输电线路防污方案及决策指标的确定

输电线路防污方案的决策涉及多个因素，是一个多指标决策过程.通过综合分析，在兼顾安全性和经济性的基础上，选用以下决策指标：防污所需技术水平，即本单位是否有相应的技术水平、是否外聘等；防污风险，如误操作、高空坠落等；防污对生产影响，即对供电负荷、售电量、供电可靠性等的影响；防污综合费用，即维修费用、生产损失费用等；防污效果，即提高输电线路防污闪性能及供电可靠性等.对于中风险输电线路，拟采用3种防污方案，即:优先防污、针对性防污、暂缓防污.

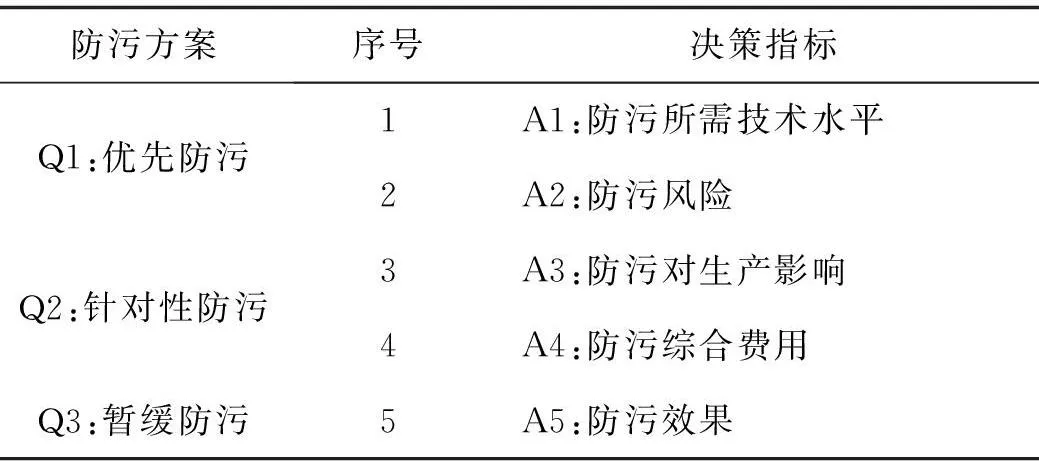
表1　输电线路防污方案及决策指标

3基于灰色关联度和TOPSIS防污方案决策模型的建立

基于灰色关联度和TOPSIS的防污方案决策模型将灰色关联度和传统理想解法的距离尺度有机结合，构造一种新的相对贴近度来实现对防污方案的评价.

基于灰色关联度和TOPSIS 防污方案决策步骤为：首先，构建原始决策矩阵并标准化，应用熵权法确定各决策指标权重，得到加权标准化矩阵; 其次，确定防污方案的正理想解和负理想解，求取各防污方案到正理想解与负理想解的欧氏距离及灰色关联度; 最后依据计算所得的相对贴近度，对防污方案进行排序优选.

3.1决策矩阵加权标准化

3.1.1构建原始决策矩阵设对m个防污方案进行决策，有n个决策指标，相应各指标值为xij(1≤i≤m,1≤j≤n)，则原始决策矩阵为x=(xij)m×n.

(1)

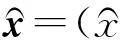
(2)

3.1.3确定决策指标权重采用熵值赋权法方法来确定各属性指标的权重[11].依据熵的定义，第j项决策指标的熵值为：

则第j项决策指标的熵权为：

(5)

决策指标权重列向量为：

W=(ω1,ω2,…,ωj,…,ωn)T

(6)

式中ωj为指标权重.

(7)

3.2计算欧氏距离与灰色关联度

3.2.1确定防污方案的正理想解和负理想解正理想解:

(8)

负理想解:

(9)

式中,J+是值越大越好的指标集合，J-是值越小越好的指标集合.

3.2.2计算各防污方案到正理想解和负理想解的欧氏距离到正理想解的距离：

(10)

到负理想解的距离：

(11)

3.2.3计算各防污方案与正理想解和负理想解之间的灰色关联度1) 第i个方案与正理想方案关于第j个指标的灰色关联系数：

(12)

则各防污方案与正理想方案的灰色关联系数矩阵为：

(13)

第i个方案与正理想方案的灰色关联度为:

(14)

2) 第i个方案与负理想方案关于第j个指标的灰色关联系数：

(15)

则各方案与负理想方案的灰色关联系数矩阵为：

(16)

第i个方案与负理想方案的灰色关联度为:

(17)

3.3防污方案的相对贴近度和优劣排序

3.3.1归一化欧氏距离和灰色关联度

(18)

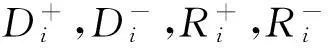
3.3.2合并归一化后的欧氏距离和灰色关联度

3.3.3相对贴近度的计算相对贴近度反映了待评防污方案与正理想解或负理想解在态势变化上的接近程度.

(21)

4算例分析

以WSCC-9系统中的污闪中风险输电线路防污方案的决策过程为例.由文献[6]可知输电线路L3为中风险线路.

4.1原始决策矩阵的构建依据表1,经领域专家的评审,得到表2的评估结果，各决策指标均采用模糊语句来表达,如:很高，很大，很好，较高，较大，好，高，一般，很低，很差等[12].

利用三角型隶属度函数脆性化模糊决策判断语句,如图2.

表2　评估结果

图2　三角型隶属度函

模糊语句的脆性系数[13]用式(22)求得

(23)

式中，K为模糊语句的脆性系数；a0，b0分别表示图2中，当隶属度为零时，每一个模糊语句值变化区间的最小值和最大值；a0#aih,h#bib0,h表示隶属度等于1时模糊语句值；取s=0,1;c,d分别为整个模糊集的下界和上界，即，c=0,d=10.

表3　各模糊语句的脆性系数

以模糊语句“较高”为例，求其脆性系数.

由图2可知a0=5,b0=9,a1=b1=7.将a0=5,b0=9,a1=b1=7及c=0，d=10代入式(22)可得：

(24)

同理可得其他模糊语句所对应的脆性系数如表3.

依据上述结果可得原始决策矩阵:

(24)

4.2归一化决策矩阵按式(24)代入式(2)中归一化为标准化矩阵.

4.3利用熵值赋权法确定各指标权重各决策指标的权重系数为：

ω1=0.176 1,ω2=0.242 9,ω3=ω4=0.187 4,ω5=0.206 2.

4.4计算加权标准化决策矩阵将指标权重向量与标准化矩阵相乘，则得到如下加权标准化矩阵.

4.5确定正理想解和负理想解防污方案各决策指标中，A1,A5属于值越大越好的集合，而A3,A4,A4属值越小越好的集合.

正理想解和负理想解分别为:

4.6计算各方案到正理想解和负理想解的距离到正理想解的距离：

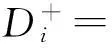
到负理想解的距离：

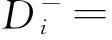
4.7计算各方案与正理想解和负理想解之间的灰色关联度

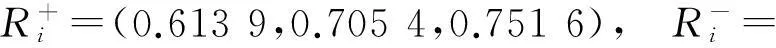
4.8归一化欧氏距离和关联度

4.9合并归一化后的欧氏距离和关联度取α1=α2=0.5，计算得：

4.10相对贴近度的计算

5结论

防污是保证电力系统安全稳定运行的重要措施，但在防污实施过程中，若不对不同输电线路的防污方案加以区分，而是一拥而上，势必会造成较大的经济损失.文中基于灰色关联度和TOPSIS的防污方案决策法采用“防污所需技术水平”、“防污风险”、“防污对生产影响”、“防污综合费用”、“防污效果”5 个对方案决策起重要作用的指标，对3个防污方案进行综合分析，确立了相应线路在保证运行安全的前提下应用的兼顾经济性的防污方案.在电力部门防污实践应用中表明该方法与已有研究成果相比更优越，可为电力系统供电防污工作提供新的思路.

6参考文献

[1] 宿志一，李庆峰.我国电网防污闪措施的回顾和总结[J].电网技术,2010,34(12):124-130.

[2] 刘琰,王俊锴.陕西电网“12.18”大面积污闪事故的分析及其防治对策[J].电网技术，2002，26(1)：82-85.

[3] 崔江流，宿志一，车文俊.2001年初东北、华北和河南电网大面积污闪事故分析[J].电力设备，2001,2(4):6-20.

[4] 高航.2001年初河南电网发生污闪事故的原因与防范措施[J].电网技术，2001,25(10):76-79.

[5] 徐喜佑.华东电网500 kV输电线路污闪的原因及对策[J].中国电力，1997,30(11):8-11,33.

[6] 帅海燕,龚庆武,陈道君.计及污闪概率的输电线路运行风险评估理论与指标体系[J].中国电机工程学报,2011,31(16):48-54.

[7] 赵新泉，彭勇行.管理决策分析[M].北京：科学出版社，2008：233-241.

[8] Chen C T.Extensions of the TOPSIS for group decision making under environment[J].Fuzzy Sets and Systems,2000,(114):1-9.

[9] 吴军，帅海燕.一种基于多方法组合的新型等值附盐密度预测模型[J].陕西电力，2011(8):13-17.

[10] 陈雷,王延章.基于熵权系数与TOPSIS 集成评价决策方法的研究[J].控制与决策，2003,14(4):456-459.

[11] 袁志坚.电力变压器状态维修决策方法的研究[D].重庆:重庆大学博士论文,2004.

[12] 董玉亮,顾煜炯,杨昆.基于灰色理论和RCM 分析的发电设备风险分析[J].动力工程,2004,24(6):798-801.

(责任编辑赵燕)

Research on anti-pollution decision-making of transmission linebased on grey correlation degree and TOPSIS

SHUAI Haiyan

(Wuhan Technical College of Communications,Wuhan 430065,China)

Abstract:To further improve the power-supply reliability,grey correlation degree (GCD) and TOPSIS decision-making model to anti-pollution of transmission line is proposed.By comprehensive analysis based on safety and economy,five decision-making indexes such as the anti-pollution technology level needed,anti-pollution risk,anti-pollution impact on production,integrated cost of anti-pollution and anti-pollution effect are selected to analyze the decision process of the anti-pollution of the transmission line,Middle Risk of Pollution-flashover in WSCC-9,and the detailed application of GCD and TOPSIS decision-making method to anti-pollution is discussed.The conclusion proves that GCD and TOPSIS decision-making method to anti-pollution of transmission line is feasible,which will provide a new thread to power-supply reliability.

Key words:transmission line; anti-pollution decision-making; grey correlation degree; TOPSIS

中图分类号:TM8

文献标志码:A

DOI:10.3969/j.issn.1000-2375.2016.03.015

文章编号:1000-2375(2016)03-0252-06

作者简介：帅海燕(1970-)，女，博士，副教授，E-mail:429569361@qq.com

基金项目：湖北省教育厅科学技术研究计划指导性项目(B20128702)资助

收稿日期:2015-06-14