基于时空分析的位置大数据挖掘方法研究

谭梦茜， 邵雄凯, 刘　春,2

(1 湖北工业大学计算机学院， 湖北 武汉 430068; 2 深圳市豪恩电子科技股份有限公司 广东 深圳 518109)

基于时空分析的位置大数据挖掘方法研究

谭梦茜1， 邵雄凯1, 刘春1,2

(1 湖北工业大学计算机学院， 湖北 武汉 430068; 2 深圳市豪恩电子科技股份有限公司 广东 深圳 518109)

[摘要]位置数据的高维特性及其数据海量的特点，使得对位置数据的挖掘较为困难。为解决这一难题，首先对高维位置数据采用基于时空约束的频率剪枝算法进行数据清洗；然后设定时间维上兴趣时间段的约束条件，提取兴趣位置点；再根据欧式距离划分与聚类划分的原理相似性，引入K-Means聚类，实现对车主地理位置关系的挖掘。通过试验可以看出，该方法较为简便的实现了对邻里、同事关系的挖掘,结果符合该区居民的地理位置分布情况，证明了该方法的适用性。

[关键词]时空分析；K-Means聚类算法；数据挖掘

位置数据是具有时空特性的数据，而时空数据挖掘是指从具有海量、高维(经度、纬度、海拔、时间、ID、加速度等维度)、高噪声和非线性等特性的时空数据中提取出隐含的、人们事先不知道的、但又潜在有用的信息及知识的过程。[1]随着集成定位系统的智能手机和车机的普及、以及位置服务应用的逐步推广，时空数据急剧增加，寻找快速高效的时空数据挖掘方法成了数据挖掘的热点和难点。

对海量的位置数据进行时空分析，可以提取其中的用户位置关系、轨迹关系、行为模式等，并可根据这些信息进行针对性信息推荐。[2]考虑到时空数据具有时间和空间的高维特性，本文首先使用基于时空约束的频率剪枝算法[3]进行数据去噪和预处理，再在时间维上设置兴趣时间段的约束条件，以缩减兴趣位置点范围，这样处理后就只需考虑移动对象位置点间的分布，从而实现了降维效果。然后利用K-Means聚类算法[4]根据位置点间的欧氏距离来划分位置数据中聚集的类，从而定义地理位置上的关联关系，并推导得出邻里关系、同事关系等隐含信息。

1位置数据预处理

1.1数据描述

试验中所用到的数据来自2013-2014年武汉市车联网测试项目中用户车辆导航收集的车辆位置数据。原始数据表中主要保存了车辆装配的导航终端采集的数据，这些数据包括记录ID、设备通讯地址、时间、经维度、加速度等字段信息。原始数据结构定义见表1。

数据结构的属性值可以看作是不同的维度，通过维度的组合分析可以提供不同视角的信息。如对加速度维度和路径(经纬度组合)维度的分析，可以推断车辆驾驶员的驾驶习惯等。本文目标是分析车主间地理位置关系，因此通过选取ID、IdObj、Latitude、Longitude、CreateTime的维度组合来进行挖掘分析。于是，二维空间中的一个移动对象(Moving Object，缩写MO)在某一时刻的位置状态可以用一个四元组表示[5]：

MOID=(idObj,lat,lon,time)

1.2基于频率剪枝算法的时空数据清洗

从海量数据中提取兴趣信息，首先需要对数据进行过滤和清洗[6]。针对提取邻里关系和同事关系的要求，对数据进行预处理，去除其中无意义的点、非工作日上传的数据等，可以缩减处理工作量，大大加快处理速度。

本文采用结合时间和空间约束的概率剪枝策略实现对车辆位置数据的预处理。其中，概率剪枝算法[7]不同于以往的有严格剪枝条件的剪枝算法，而是根据具体问题中的概率因素来决定剪枝条件，对不太可能影响结果的最小-最大值的子树进行剪枝。

概率剪枝算法中的空间和时间约束主要是指设置在所研究空间的最小外包矩形MBR，包括经纬度大小以及所研究时间段的区间。[3]此方法降噪的基本思想是，设定所研究的空间和时间范围，对在该范围上传位置数据的每个用户分别计算每天上传的位置数据量，如果小于每天最低上传频率值Fremin，则判为无效数据，删除用户该天的位置信息。

基于时空约束的频率剪枝算法如下：

限定时间约束(time[])为非节假日时间，空间约束为武汉市江汉区和江岸区部分区域所在的经纬度lat[]∈(30.589325-30.648855),lon[]∈(114.22754-114.317568),频率约束Fremin= 1000。

for each user in 数据集合MO[]

idObj = Cur_user

for each point in idObj的位置点集合

MO[n] = Cur_point

if MO[n].t∈{time[]} && MO[n].l∈{lat[],lon[]}

n++

end if

end for

if n < Fremin

idObj为无效用户，删除其相关信息

end if

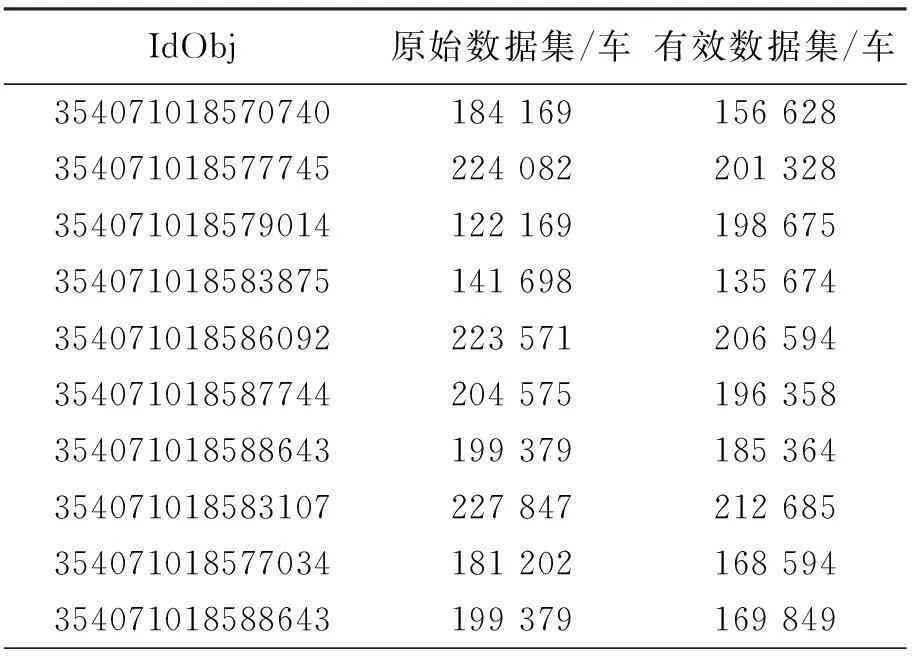
通过随机抽取10组用户上传的位置数据集合，采用上述方法进行预处理，结果如表2所示，证明该剪枝算法的有效性。经过上述处理后，可以得到江汉区和江岸区部分区域范围内工作日上传的有效位置数据。

1.3时空数据的降维处理

为了从每天的位置数据中提取出车主小区位置点和公司位置点，需要对位置数据的时变特征进行直观的定性描述[8]。

本文将以上数据按每10 min

的时间片段等间隔统计各片段内上传的数据，得到时间曲线图(图 1)。图中，横轴表示等间隔取样的片段，纵轴表示每间隔中上传的数据量。从图中可看出上下班高峰期分别在7∶20-9∶20和17∶00-19∶00时间段。所以，将时间维上的约束条件限定为7∶00-9∶40、16∶50-23∶59时间段范围内，并且各时间段开始后20 min、结束前20 min的任一时间段内无上传数据，以确保所选的两个上下班时间段内的第一和最后一条数据能代表小区坐标位置和公司坐标位置。通过限定正常情况下上下班位置数据出现的时间，使得在聚类过程中进一步剔除噪声数据，降低噪声数据对算法的影响。

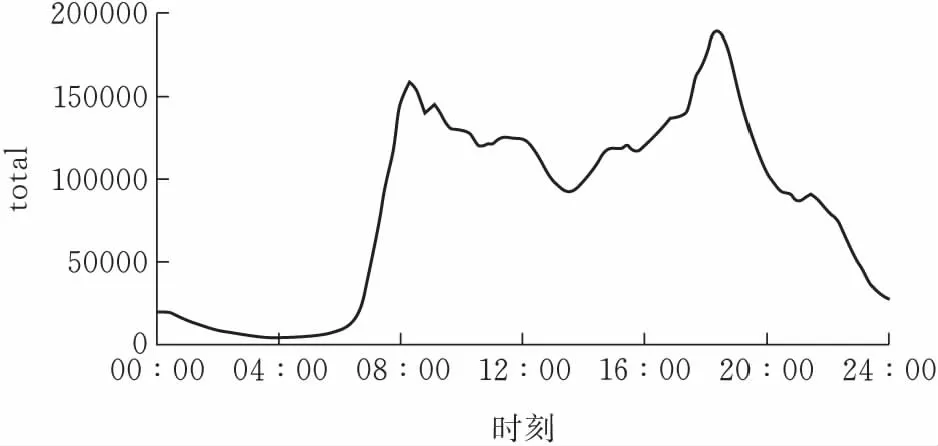
图1　时间分布规律图

经过上述处理后，选取各用户上传的30 d数据。这样，数据挖掘的对象是满足时间约束条件的各用户上传天数达30 d的坐标位置数据，数据挖掘的过程只用考虑移动对象位置点的分布。

综上，研究的对象从具有时空关系的四元组对象转换为表示二维空间中的移动对象位置点的三元组：

MOID=(idObj,lat,lon)

1.4数据可视化

对清洗前和清洗后的数据进行可视化表达分别如图2、图3。从图中可以看出，图2中的原始数据分布符合武汉主城区沿长江和湖泊分布的情况。经过清洗后，图3中的数据量明显减少，但是能更准确地反映位置数据分布情况。针对清洗后的数据，选取上班时间段内前三分钟的坐标和下班时间段内最后三分钟的坐标，作为邻里位置表；选取上班时间段最后三分钟内的坐标和下班时间段内前三分钟的坐标，作为公司位置表。然后，分别对邻里位置表和公司位置表进行K-Means聚类分析。

取剪跨比λ为4，配筋率ρl为0.96%、壁厚t为100 mm，不同轴压比ηk的三种矩形空心墩，轴压比分别为0.1、0.2、0.3，进行Pushover分析，其对应的能力曲线如图10所示，由图10可知，轴压比增加1倍，空心墩的承载能力增加近50%，同时空心墩位移延性随着轴压比的提高而有所降低。

图 2　清洗前的数据分布图

图 3　 清洗后的数据分布图

2基于K-Means聚类的位置数据挖掘方法

2.1k-Means算法的适用性

为了挖掘位置点空间意义上的相近关系，即邻里关系、同事关系，本文依据位置点间的欧式距离的远近来划分位置数据集中聚集的类。而K-Means聚类算法采用距离作为相似性的评价指标，即认为两个对象之间的距离越近，其相似性就越大。这与本文对位置点聚类所要达到的效果一致。同时，K-Means算法在处理大规模数据集时，其算法效率较高，适合对大规模数据集进行高效聚类。[9]所以本文选用K-Means聚类算法进行位置邻近关系的划分[10]。

对经纬度位置数据进行K-Means聚类的流程[11]如下：在位置数据中随机抽取K个点作为聚类中心，然后遍历其余位置并根据欧式距离来找到距离各自最近的聚类中心点，将其加入到该聚类中。然后各聚类通过误差平方和这个准则函数E来调整该聚类的聚类中心点，并将这个点作为下一次聚类的聚类中心。依次迭代，直到某一次迭代出的聚类中心和上一次的聚类中心相差的距离小于某个标准，则迭代结束。

在K-Means 聚类中，影响聚类效果的关键因素是聚类中心点的选取和类别数目的确定。随机选择聚类中心可能造成聚类中心过于居中或者不能均匀地分散在整个数据空间，导致收敛所需迭代次数增多，甚至陷入局部最优解，影响聚类结果的准确性。[9]而从图3中，可以看出位置数据分布在部分区域密集，部分区域相对分散，所以本文结合位置数据分布的特点利用最小最大法来选择聚类中心，即首先选择所有对象点中相距最远的两个对象点作为聚类中心，然后选择第三个聚类中心点，使得它与之前确定的两个点距离的较小值大于其余对象点与这两个聚类中心点距离的较小值，以后的聚类中心点也按照同样的原则选取。[11]而对于类别数目的确定，通过试验证明聚类数为12时，聚类效果最好。

2.2时空分析流程

基于上述分析，本文设计出针对坐标位置数据的时空关系分析流程[12-13]：

步骤1在位置数据集合MO[]中依据最小最大法选取k个初始聚类中心点Zj(MOID), ID=1,2,3,…,n;j=1,2,3,…,k.经试验证明k=12时，聚类效果最好，所以令k=12；

步骤2在n次迭代中，计算每个位置点与各聚类中心点的欧式距离D(MOID,Zj(MOID)),ID=1,2,3,…,n;j=1,2,3,…,k.若满足D(MOID,Zk(MOID))=min{D(MOID,Zj(MOID)),

j=1,2,3,…,k}，则MOID∈wk,其中Wk为第k个聚类；即把位置点调整到K个类别中的离它最近的类别；

步骤3由步骤2得到新的聚类，计算误差平方和准则函数Jc(I)，I表示迭代次数。按照使Jc(I)最小的原则确定新的聚类中心。Jc(I)的表达式为:

步骤5如此重复步骤2，直到前后两次迭代得到的聚类中心一模一样。

通过K-Means算法分别对邻里位置和公司位置进行聚类后，将同一个聚类中位置点的车主间关系定义为邻里关系或同事关系。

3结果分析

本文对武汉市江汉区和江岸区部分区域(图4)的车辆位置大数据采用K-Means聚类分析后，将聚类数据进行可视化表示，得到邻里关系聚类图(图5)、同事关系聚类图(图6)，图中不同的图标形状代表了不同的聚类。从聚类结果图中可发现，图5中的聚类主要集中在江汉区和江岸区的小区住宅处，并呈现沿各主干道和江岸分布的特点，图6中的聚类分布较为分散，符合该地区公司较多且分散的事实。通过以上分析，聚类结果能准确反映武汉市该地区居民的邻里位置和公司位置分布情况。

图 4　江汉区和江岸区的研究范围

图 5　邻里关系聚类图

图 6　同事关系聚类图

本文所使用的基于K-Means位置数据分析方法也存在一定的不足：首先，该方法仅使用了K-Means空间聚类法，并没有与现有的道路地图相结合[10]；其次，该方法通过在时间维上设置约束条件的方式，来选取小区位置点、公司位置点，这种选取办法适用于居民正常上下班的情况，而对于上晚班或上班时间自由等情况，则不适用。这些都是今后的改进方向。

4结束语

通过分析具有时空关系的位置数据，可以发现、提取或总结出很多有价值的信息，从而帮助我们更好地研究车辆驾驶人的聚类关系、行为关系，并可以进行针对性的个性化数据推荐。本文对位置数据进行数据清洗后，提取上下班时间段的位置点，并采用K-Means聚类方法挖掘位置数据之间隐藏的车主间地理位置关系的信息。以上对位置数据进行的试验，能较好地分析出位置点聚集的簇，证明了该方法在实践中的适用性。

[参考文献]

[1]刘大有,陈慧灵,齐红,等.时空数据挖掘研究进展[J].计算机研究与发展，2013,50(2):225-239.

[2]龚玺,裴韬,孙嘉,等.时空轨迹聚类方法研究进展[J].地理科学进展，2011,30(5):522-534.

[3]邹永贵,万建斌,夏英.基于路网的LBSN用户移动轨迹聚类挖掘方法[J].计算机应用研究, 2013,30 (08):2410-2414.

[4]席景科,谭海樵.空间聚类分析及评价方法[J].计算机工程与设计，2009,30(07):1712-1715.

[5]Liu Xiaohua, Huang Jiejun, Wan Youchuan, et al. Logical expression of feature-based spatio-temporal data model research: 2nd international conference on information engineering and computer science - proceedings, ICIECS .2010[C]. IEEE Computer Society, 2010.

[6]Han J, Kamber M, PEI J. Data Mining：Concepts and Techniques [M]. 3nd ed.范明,孟小峰,译.数据挖掘概念与北京：机械工业出版社,2012:55-79.

[7]纪洪生.基于概率的剪枝算法[J].电脑知识与技术，2006,32(11):99-100.

[8]王涛,王俊峰,罗积玉,等.基于时空分析的复杂交通流数据挖掘算法[J].四川大学学报(工程科学版)，2011,43(5):153-158.

[9]沈吟东,张仝辉,徐甲.基于K-means聚类算法的公交运营时段分析[J].交通运输系统工程与信息，2014,14(2):87-93.

[10] 吕玉强,秦勇,贾利民,等.基于出租车GPS数据聚类分析的交通小区动态划分方法研究[J].物流技术，2010(5):86-88,135.

[11] 熊忠阳,陈若田,张玉芳.一种有效的K-means聚类中心初始化方法[J].计算机应用研究，2011, 28(11):4188-4190.

[12] 黄韬,刘胜辉,谭艳娜.基于k-means聚类算法的研究[J].计算机技术与发展， 2011,21 (7):54-57,62.

[13] Manish V, Mauly S, Neha C, et al. A comparative study of various clustering algorithms in data mining [J]. International Journal of Engineering Research and Applications. 2012,2(3):1379-1384.

[责任编校： 张岩芳]

Big Location Data Mining Research Based on Spatial and Time Analysis

TAN Mengxi1, SHAO Xiongkai1, LIU Chun1,2

(1SchoolofComputerScience,HubeiUniv.ofTech.,Wuhan430068;2LonghornTechnologyCo.,Ltd,Shenzhen518109,China)

Abstract：The multi-dimensional and massive characteristics of location data result in the difficulty of location data mining. In the study, we firstly used the frequency pruning method based on spatial-time constraints to clean and trim the data. Secondly, we extracted the position data we’re interested in by setting the constraint condition on the time dimension. Finally, according to the similarity between clustering and location coordinate classification, we used K-Means cluster analysis to mine the geographic relationship among cars owners from the location data. The experimental results show that the K-Means cluster analysis on the location data is able to quickly mine the geographic relationship among car owners, and the result conforms to the location distribution in the researched area.

Keywords：Spatial-time analysis; K-Means algorithm: Data mining

[收稿日期]2015-06-23

[基金项目]湖北省自然科学基金(2014CFB594)

[作者简介]谭梦茜(1991-)， 女，湖北宜城人，湖北工业大学硕士研究生，研究方向为大数据分析与挖掘

[文章编号]1003-4684(2016)02-0053-05

[中图分类号]TP311

[文献标识码]：A

通讯地址表1原始数据结构定义字段名含义ID记录IDIdObj终端Latitude纬度Longitude经度Altitude海拔Accelerometer_X纬度方向上的加速度Accelerometer_Y经度方向上的加速度Accelerometer_Z海拔方向上的加速度CreateTime时间戳 其中，下标ID表示这是移动对象的第ID条记录；idObj是移动对象的终端，也可代表不同用户；time是当前记录的时间戳；lat和lon表示移动对象在time时刻所处经纬度坐标。