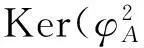[A,[A,X]] = 0 的解空间

廖军,吴佐慧,刘合国

(湖北大学数学与统计学学院，湖北 武汉 430062)



[A,[A,X]] = 0 的解空间

廖军,吴佐慧,刘合国

(湖北大学数学与统计学学院，湖北 武汉 430062)

摘要：设A是复数域C上的n阶方阵.本文中确定方程[A,[A,X]]=0的解空间的一组基以及维数.方程[A,[A,X]] =0的解空间即线性空间Mn×n(C) 上线性变换φA(X)=[A,X]=AX-XA平方的核空间.

关键词：维数空间；基；斜线性变换；解空间

0引言

记C为复数域.设A∈Ml×l(C),B∈Mm×m(C).定义线性空间V=Ml×m(C) 上的线性变换φAB，

φAB(X)=AX-XB对任意的X∈V,

1引理和结论

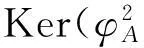
引理1.1设φ是域F上线性空间W的线性变换.则Ker(φ)∩Im(φ)的一组基的原像和Ker(φ)的一组基一起构成Ker(φ2) 的基.特别地,dim(Ker(φ2))=dim(Ker(φ))+dim(Ker(φ)∩Im(φ)).

引理1.1的证明设α1,α2,…,αr和γ1,γ2,…,γs分别是Ker(φ)和Ker(φ)∩Im(φ)的基.设βi是γi在φ下的一个原像.下面我们证明α1,α2,…,αr,β1,β2,…,βs是Ker(φ2)的一组基.任取α∈Ker(φ2).则φ2(α)=0.因此φ(α)∈Ker(φ)∩Im(φ),于是存在域F中的元l1,l2,…,ls使得

φ(α)=l1γ1+l2γ2+…+lsγs.则有φ(α)=l1φ(β1)+l2φ(β2)+…+lsφ(βs)=φ(l1β1+l2β2+…+lsβs).因此φ(α-(l1β1+l2β2+…+lsβs)) = 0,即α-(l1β1+l2β2+…+lsβs)∈Ker(φ).所以,存在域F中的元k1,k2,…,kr使得

α-(l1β1+l2β2+…+lsβs)=k1α1+k2α2+…+krαr,

由此得到α=k1α1+k2α2+…+krαr+l1β1+l2β2+…+lsβs.

下面只需证明α1,α2,…,αr,β1,β2,…,βs线性无关即可.设

k1α1+k2α2+…+krαr+l1β1+l2β2+…+lsβs=0.取其在φ下的像得l1γ1+l2γ2+…+lsγs=0.又由于γ1,γ2,…,γs是Ker(φ)∩Im(φ)的基,则l1=l2=…=ls=0.由此得k1α1+k2α2+…+krαr=0.又α1,α2,…,αr是Ker(φ) 的基,则k1=k2=…=kr=0.所以有k1=k2=…=kr=l1=l2=…=ls=0,即α1,α2,…,αr,β1,β2,…,βs线性无关.综上,α1,α2,…,αr,β1,β2,…,βs是Ker(φ2)的基.特别地,dim(Ker(φ2))=dim(Ker(φ))+dim(Ker(φ)∩Im(φ)).

设eij是(i,j)位置是1,其他位置全为0的矩阵.记Nl=e21+e32+…+el l-1,这里Nl∈Ml×l(C).

引理1.2定义Ml×m(C)上的一个线性变换φlm,使得φlm(X)=NlX-XNm对任意的X∈Ml×m(C)成立.则

1)el1,el2+el-1 1,…,el min{l,m}+el-1 min{l,m}-1+…+el-min{l,m}+1 1是Ker(φlm)的一组基.

2)eij,i-j>min{l-m,0}；eij-e1,j-i+1,i-j≤min{l-m,0}是Im(φlm)的一组基.

引理1.2的证明设X=∑xijeij.为方便起见,记el+1 j=ei,0=0.则

φlm(X)=NlX-XNm=∑xij(ei+1 j-ei j-1).

因此,ei+1 j-ei j-1,1≤i≤l,1≤j≤m生成Im(φlm).又

〈1≤i≤l,1≤j≤m〉=〈eij,i-j>min{l-m,0};eij-e1,j-i+1,i-j≤min{l-m,0}〉.

显然,向量组eij,i-j>min{l-m,0};eij-e1,j-i+1,i-j≤min{l-m,0}线性无关，因而它是像空间的一组基.特别地，dim(Im(φlm))=lm-min{l,m}.

由于dim(Im(φlm))+dim(Ker(φlm))=lm,则dim(Ker(φlm))=min{l,m}.又el1,el2+el-1 1,…,el min{l,m}+el-1 min{l,m}-1+…+el-min{l,m}+1 1是Ker(φlm)中min{l,m}个线性无关的向量组,因此,el1,el2+el-1 1,…,el min{l,m}+el-1 min{l,m}-1+…+el-min{l,m}+1 1是Ker(φlm)的基.

由Ker(φlm)以及Im(φlm)易求得Ker(φlm)∩Im(φlm).

引理1.31) 当i-j≥1,φlm(ei-1 j+ei-2 j-1+…+ei-j 1)=eij.

2) 当i-j≥l-m+1时，-φlm(ei j+1+ei+1 j+2+…+el l-i+j+1)=eij.

3) 当i

4) 当l

进一步,Ker(φlm)∩Im(φlm)的一组基的原像集为：

1) 当l>m时，el-1 i+2el-2 i-1+…+iel-i 1，i=1,2,…,m.

2) 当l=m时，el-1 i+2rl-2 i-1+…+iel-i 1,i=1,2,…,l-1.

3) 当l

引理1.3的证明注意到φlm(eij)=ei+1 j-ei j-1.

由此即可得到相应的结论.

如果存在可逆矩阵U使得A=UBU-1,则X∈Ker(φA)当且仅当U-1XU∈Ker(φB),Y∈Im(φA)当且仅当U-1YU∈Im(φB).因此,研究φA时,可以假设A是若当矩阵.设

对Mn×n(C) 作相应的分块.若X∈Mn×n(C),记X=(Xij)r×r,其中Xij∈Mni×nj(C)是位于(i,j)位置的块.记Y=φA(X)=AX-XA.则Yij=(λiIni+Nni)Xij-Xij(λjInj+Nnj)=(λi-λj)Xij+(NniXij-XijNnj).当λi≠λj时,Yij=0只有零解.如果λi=λj,则Yij=NniXij-XijNnj.记φij=φninj.

定理1.4[3]设φA(X)=AX-XA,其中A,X∈Mn×n(C) 且

设

则

1) 当l

2) 当l=m时，el1,el2+el-1 1,…,ell+el-1 l-1+…+e11;el-1 i+2el-2 i-1+…+iel-i 1,i=1,2,…,l-1.

注记1.5注意到上述方法对φAB(X)=AX-XB，其中A∈Ml×l(C)，B∈Ml×m(C)同样适用.

推论1.6[1,3]设A的初等因子为(λ-λi)nij其重数为mij，i=1,2,…,r,j=1,2,…,ei.则

2参考文献

[1] Gracia J M.Dimension of the solution spaces of the matrix equations[A,[A,X]]=0 and[A[A,[A,X]]]=0[J].Linear and Multilinear Algebra,1980(9):195-200.

[2] Jacobson N.Lectures in abstract algebra(II):linear algebra[M].New York:Springer,1953.

[3] Liao J,Liu H,Wang Y,et al.Generalization of Gracia’s results[J].Electronic Journal of Linear Algebra,2015,30:243-252.

[4] Wedderburn M.Lectures on matrices[M].New York American Mathematical Society Colloquium Publications,2008.

(责任编辑赵燕)

The solution space of[A,[A,X]]=0

LIAO Jun,WU Zuohui,LIU Heguo

(School of Mathematics and Statistics,Hubei University,Wuhan 430062,China)

Abstract:Let C be the complex number field.Suppose that A∈Mn×n(C).Define a transformation φAof Mn×n(C) by φA(X)=[A,X]=AX-XA for X∈Mn×n(C).The basis and dimension of the kernel ) of are determined explicitly,which refines some known results.

Key words:dimensional famula;basis;linear harsfur mation;solution spaces

中图分类号:O614.12

文献标志码:A

DOI:10.3969/j.issn.1000-2375.2016.03.001

文章编号:1000-2375(2016)03-0179-03

作者简介：廖军(1979-)，男，博士，讲师

基金项目：国家自然科学基金(11371124,11401186) 和“高等代数”湖北省精品课程专项基金资助

收稿日期:2015-11-30