四边形变式问题的解题策略

杨东兴

“让学生受到观察、联想、类比、归纳、猜想、抽象概括、分析和综合等方法的熏陶，发挥数学学科重视考察学生的基础能力，着眼于发展学生综合能力的特点.”近几年来数学中考的变式题型就体现了这个特点，尤其是每年各地市的试卷里都有关于四边形综合题的变式题.这类题也是中考中难度较大的一类题.那么，变式题有哪些特点呢？有没有什么好的解决方法呢？下面我们就以近年来黑龙江省各地市的一些中考题为例进行说明.

例1：（2014年 黑龙江省绥化市）在菱形ABCD和正三角形BGF中，∠ABC=60°，P是DF中点，连接PG，PC.

（2）如图2，当点F在AB的延长线上时，线段PC，PG有怎样的数量关系，写出你的猜想，并给予证明；

（3）如图3，当点F在CB的延长线上时，线段PC，PG又有怎样的数量关系，写出你的猜想.（不必证明）

【点评】

本题主要考察了菱形的性质，以及全等三角形的判定等知识点.根据已知和所求的条件正确地构建出相关的全等三角形是解题的关键.

例2：（2015年 黑龙江省龙东地区）如图，四边形ABCD是正方形，点E在直线BC上，连接AE将△ABE沿AE所在直线折叠，点B的对应点B'，连接AB'，并延长直线交DC于点F.

（1）当点F与点C重合时如图4，易证：DF+BE=AF（不需证明）；

（2）当点F在DC的延长线上时如图5，当点F在CD的延长线上时，如图6，线段DF，BE，AF有怎样的数量关系？请直接写出你的猜想，并选择一种情况给予证明.

【解析】

根据折叠的图形全等这个特点得出全等，再根据正方形对角线平分角相等，得到相等的边，然后根据等量代换得到需要证明的结论，第（2）问中图5、图6与图4证明方法相同，并且同学们通过仔细观察，能够得出正确的数量关系，图5：DF+BE=AF，图6：DF+AF=BE，证明过程同第（1）问.

【点评】

这是一道四边形综合题.本题主要考察正方形的性质，全等三角形的判定等知识，找出全等关系是解题关键.

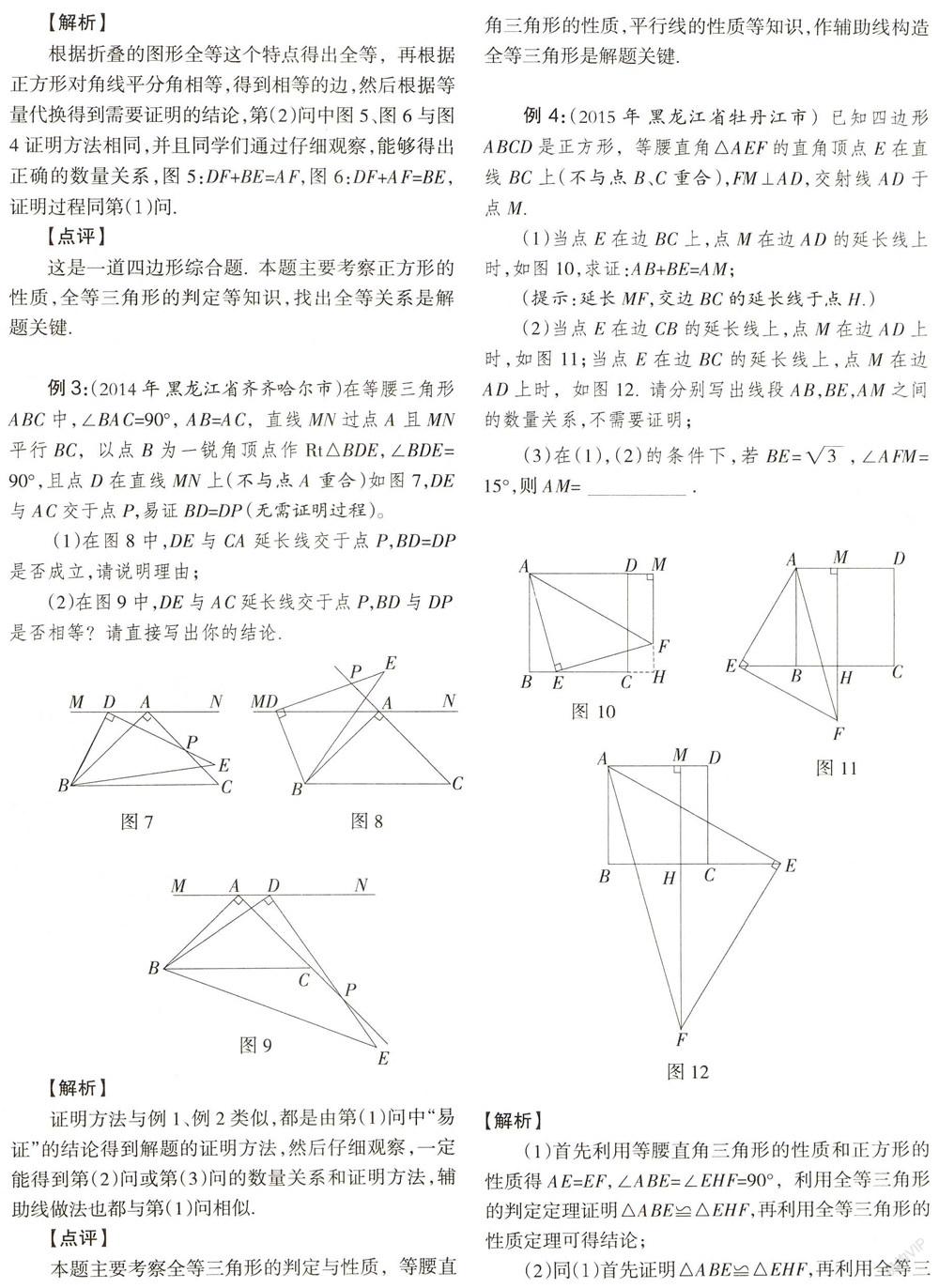
例3：（2014年 黑龙江省齐齐哈尔市）在等腰三角形ABC中，∠BAC=90°， AB=AC，直线MN过点A且MN平行BC，以点B为一锐角顶点作Rt△BDE，∠BDE=90°，且点D在直线MN上（不与点A重合）如图7，DE与AC交于点P，易证BD=DP （无需证明过程）。

（1）在图8中，DE与CA延长线交于点P，BD=DP是否成立，请说明理由；

（2）在图9中，DE与AC延长线交于点P，BD与DP

是否相等？请直接写出你的结论.

【解析】

证明方法与例1、例2类似，都是由第（1）问中“易证”的结论得到解题的证明方法，然后仔细观察，一定能得到第（2）问或第（3）问的数量关系和证明方法，辅助线做法也都与第（1）问相似.

【点评】

本题主要考察全等三角形的判定与性质，等腰直角三角形的性质，平行线的性质等知识，作辅助线构造全等三角形是解题关键.

例4：（2015年 黑龙江省牡丹江市）已知四边形ABCD是正方形，等腰直角△AEF的直角顶点E在直线BC上（不与点B、C重合），FM⊥AD，交射线AD于点M.

（1）当点E在边BC上，点M在边AD的延长线上时，如图10，求证：AB+BE=AM；

（提示：延长MF，交边BC的延长线于点H.）

（2）当点E在边CB的延长线上，点M在边AD上时，如图11；当点E在边BC的延长线上，点M在边AD上时，如图12. 请分别写出线段AB，BE，AM之间的数量关系，不需要证明；

【解析】

（1）首先利用等腰直角三角形的性质和正方形的性质得AE=EF，∠ABE=∠EHF=90°，利用全等三角形的判定定理证明△ABE≌△EHF，再利用全等三角形的性质定理可得结论；

（2）同（1）首先证明△ABE≌△EHF，再利用全等三角形的性质定理可得结论；

（3）利用分类讨论的思想，首先由∠AFM=15°，易得∠EFH，由△ABE≌△EHF，根据全等三角形的性质易得∠AEB，利用锐角三角函数易得AB，利用（1）（2）的结论，易得AM.

【点评】

本题考查的仍是四边形综合题. 本题主要考查了等腰直角三角形的性质，正方形的性质，全等三角形的性质及判定定理.数形结合、分类讨论和前面问题的结论是解答此题的关键.

以上几道中考变式题有一个共同的特点：通过适当的变化，在问题情境中运用已经学过的知识来解决问题. 同学们做这类题的时候不要紧张，要先审好题，一般第一问中的证明方法也同样适用于其他问题，其次是仔细观察图形的变化和所求的数量关系产生的变化，然后利用已知图形的性质，做相应的辅助线来证明等等。做辅助线的正确与否是解题关键点，也是难点.只要同学们在日常练习中认真学习，归纳日常练习或测试中做过的这类题型的辅助线做法，就能达到“心中有数”，所以此类变式题，看似变化莫测，实则百变不离基础.功夫在平时，重在积累、归纳、抓住规律.