2015年安徽物理高考压轴题的多种解法及教学启示
2016-05-26杨海青孙明西
杨海青 孙明西
高考是风向标,高考能充分体现最新的教育教学研究成果,能反映最前沿的新课程理念,能折射出高校及社会的人才观,所以高考试题研究对本学科教学及优秀拔尖人才培养有着很好的指导性意义.我们试从对2015年安徽物理高考压轴题的多种解法出发,研究高考命题意图,获取对中学物理日常教学的启示,为教学改革寻求导向.
2015年安徽高考理科综合的物理压轴题命题角度较为新颖,以万有引力为知识背景,以星体系的圆周运动为物理情境,以受力分析、几何图形特征分析等为能力立意点,全面考查学生能否独立的具体问题具体分析,考察学生审题能力及理想化模型、合成分解的思想,综合应用数学知识及物理规律分析解决问题能力;试题看似很平淡的给出三颗星体的质量、正三角形条件,却需要学生深层次的理解三星系统特征,创新的构建几何图形并分析几何特征,充分体现了安徽高考考试说明中学习能力、应用能力及实验与探究能力的三大能力要求,对中学物理教学及学生能力培养有很好的导向性意义,是一道成功有亮点的压轴题.
1 原题再现及解析
原题 (2015安徽理综24题)由三颗星体构成的系统,忽略其他星体对它们的作用,存在着一种运动形式:三颗星体在相互之间的万有引力作用下,分别位于等边三角形的三个顶点上,绕某一共同的圆心O在三角形所在平面内做相同角速度的圆周运动(图1为A、B、C三颗星体质量不相同时的一般情况),若A星体质量为2m,B、C两形体的质量均为m,三角形的边长为a,求: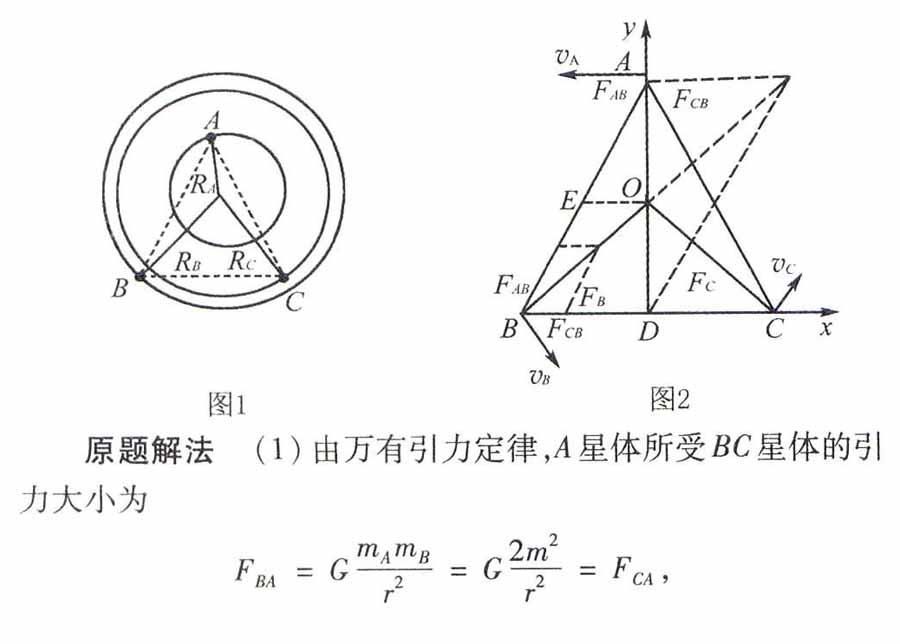


解法评析 新增的这三种解法,有一个明显的共同特征就是数学性,都是在以数学思维思考、分析物理问题,由于是任意三角形,为平时很少训练,形成试题独特的难点和立意.解法二利用力的数学向量属性,向量的模长对应的物理意义即为力的大小;解法三利用数学三角函数中的余弦定理来解决物理力的矢量三角形;解法四利用相似三角形,对应边成比例的几何关系解决物理问题 每一种解法,都是一种创新,都体现了数学和物理的紧密联系.由此可见本题以能力立意命制,意在突出对考生“运用几何图形、函数图象等进行表达分析”这一用数学工具解决物理问题的能力的考查.该压轴题是对考试说明中“物理学和数学的关系密切.高考试题的解答,不仅对几何、三角、代数、解析几何等有一定的要求,对极限、微元等思想方法也有初步的要求” 这一论述的极好体现.
教学启示 基于以上研究,我们认为,中学物理日常的教学工作这样做可能更好:(1)加强物理专业理论学习和教育理论学习,既要注重对学生基础知识和基本能力的教学,更要准确理解物理学的思想和内涵,注重学生科学素养以及创新思维能力的培养,提升的教学理念,形成正确人才观,做到教育有理想,教学有方法.(2)结合新课程标准、考试大纲及考试说明,认真研读高考试题,体会高考试题是如何体现新课程标准、考纲及其说明中的有关要求及论述的,做到备考有依据.(3)学科间,尤其是物理与数学学科间加强整合,培养学生空间想象力、数形结合思想,强化学生用数学思维分析物理问题的意识,提升学生应用数学知识方法进行逻辑推演解决物理问题的能力.(4)注重培养学生独立的灵活的应用物理知识处理问题能力,提高学生创新思维品质.
2.2 关于第三小问的多种解法
解法五 质心运动定理
由质心运动定理,星体A、B、C三颗星体构成的系统其质心的运动就好像星体的全部质量都集中于此,而且所有外力也都集中作用在其上的一个质点的运动一样,由此分析可知三颗星体做圆周运动的圆心即为其质心.建立如图2坐标系,由质心位置的坐标公式得
解法评析 新增的解法中,处理问题从整体出发,不再纠结于某一个星体,以整体性的思维看待多物体组成的系统,从质心角度和守恒的思想分析思考问题.解法五,星体A、B、C构成多物体系统,模型建构为质点系运动问题,星体A、B、C绕质心做匀速圆周运动,进而将问题转化为求解质心.解法六,将三星体归为多物体问题、系统性问题,综合使用质心运动定理和动量守恒定律,以及运用几何关系分析解决这一物理问题,这两种解法在视野上更大气,在解题方法上更灵活、创新,在物理思维品质和物理学科内涵上更具整体性、聚合性.
教学启示 基于以上分析研究,中学物理日常教学,可以采取这些目标定位:(1)启发式教学,注重方法培养.物理学有很多科学方法如:比较法、分析综合法、归纳演绎法、理想化方法、类比法、等效法、对称法等,而科学方法的教育需要重过程,教学过程中要给学生留出足够的思考与顿悟的时间与空间.(2)精心设计问题链,培养学生的强烈的问题意思,使学生在学习物理知识的同时逐步建立正确的物理学科思想和方法,物理学科思想有对称的思想、整体性思想、守恒的思想等,在教学中可设计问题链启发引导学生有序思考、感悟,培养学生深层次的理解力和深刻性的物理思维.(3)系统化训练,立足能力培养.安徽卷高考考试大纲及考试说明都对考生能力的要求进行了论述,这些能力在高考试题中都有明显的体现,也是高考命题的主要立意角度.能力的培养在教学中应常规化、系统化,尤其要突出对深层次分析解决问题解决能力的培养,在系统化的训练中提升学生独立的灵活的分析解决问题能力,提升学生创新解决问题意识.
