MPPIE:基于消息传递的RDFS并行推理框架*
2016-05-25吕小玲冯志勇饶国政张小旺许光全
吕小玲,王 鑫,3+,冯志勇,饶国政,张小旺,许光全
1.天津大学计算机科学与技术学院,天津3000722.天津市认知计算与应用重点实验室,天津3000723.南大通用数据技术股份有限公司,天津300384
ISSN 1673-9418 CODEN JKYTA8
Journal of Frontiers of Computer Science and Technology
1673-9418/2016/10(04)-0451-15
MPPIE:基于消息传递的RDFS并行推理框架*
吕小玲1,2,王鑫1,2,3+,冯志勇1,2,饶国政1,2,张小旺1,2,许光全1,2
1.天津大学计算机科学与技术学院,天津300072
2.天津市认知计算与应用重点实验室,天津300072
3.南大通用数据技术股份有限公司,天津300384
ISSN 1673-9418 CODEN JKYTA8
Journal of Frontiers of Computer Science and Technology
1673-9418/2016/10(04)-0451-15
E-mail: fcst@vip.163.com
http://www.ceaj.org
Tel: +86-10-89056056
* The National Natural Science Foundation of China under Grant Nos. 61373035, 61100049, 61373165 (国家自然科学基金); the National High Technology Research and Develfopment Program of China under Grant No. 2013AA013204 (国家高技术研究发展计划(863计划)).
Received 2015-06,Accepted 2015-08.
CNKI网络优先出版: 2015-08-12, http://www.cnki.net/kcms/detail/11.5602.TP.20150812.1623.002.html
Key words: resource description framework (RDF); RDFS inference; message passing; Pregel; parallel inference
摘要:随着语义Web的快速发展,RDF(resource description framework)语义数据规模呈现爆炸性增长趋势,大规模语义数据上的推理工作面临严峻挑战。基于消息传递机制提出了一种新的RDFS(RDF schema)并行推理方案。利用RDF图数据结构,建立RDFS推理过程的图上加边模型。以顶点为计算中心,根据不同推理模型,向其他顶点传递推理消息,完成推理操作。当所有推导出的新三元组以边的形式加入原RDF图中时,整个推理过程结束。在基于消息传递模型的开源框架Giraph上,实现了RDFS并行推理框架MPPIE(message passing parallel inference engine)。实验结果表明,在标准数据集LUBM和真实数据集DBpedia上,MPPIE执行速度均比当前性能最好的语义推理引擎WebPIE快一个数量级,且展现了良好的可伸展性。
关键词:资源描述框架(RDF);RDFS推理;消息传递;Pregel;并行推理
1 引言
近年来,语义Web得到了快速的发展,行业应用数据越来越多地选用资源描述框架(resource description framework,RDF)格式进行发布,语义数据规模呈现爆炸性增长。截至2014年4月,LOD(Linked Open Data)收集的RDF数据集已经超过了1 000个[1]。大规模RDF数据的异构性对语义数据的管理工作提出了新挑战,而RDF推理使数据管理的复杂性进一步加深[2]。如何能够高效解决大规模RDF数据的推理问题成为许多研究工作的焦点。
并行化推理方案能够有效地利用并行计算技术解决大规模RDF数据的推理问题[2]。目前已有基于集群的并行推理算法[3-5]和基于新型硬件的并行推理算法[6-8]等相关的推理工作研究,然而这些解决方案仅将传统的推理技术直接迁移到对应的并行计算框架之中,并未充分利用数据原有的特性,致使推理效率低下。针对这些问题,本文提出了一种基于消息传递机制的新方法来处理RDF模式(RDF schema,RDFS)并行推理问题。
利用RDF数据的图结构,将推理产生新三元组的过程映射为在图上的两顶点之间添加新边的过程。基于消息传递机制设计并实现了RDFS并行推理框架MPPIE(message passing parallel inference engine)。MPPIE对RDFS推理规则进行分析,采用高效的规则执行顺序,减少推理中的迭代操作,提高推理效率。以顶点为计算中心,顶点间通过消息传递进行通信。通过实验与当前性能最好的开源推理引擎WebPIE(Wed-scale parallel inference engine)[4]进行对比,在标准数据集LUBM和真实数据集DBpedia上进行测试的结果表明,MPPIE的执行性能比WebPIE高一个数量级。
本文的主要贡献如下:
(1)结合RDF数据的图结构特点,提出了将推理抽象成在图上两个顶点之间添加新边的思想,有效地利用了数据本身的结构特性。
(2)提出了一种高效的规则执行机制,减少了推理迭代次数,提高了推理执行效率。
(3)基于消息传递机制,设计了一种新的RDFS并行推理算法,以自然的方式执行推理过程。
(4)在Apache Giraph(http://giraph.apache.org/)框架下,实现了RDFS并行推理框架MPPIE。实验表明,MPPIE执行速度比基于MapReduce的推理算法快一个数量级以上。
本文组织结构如下:第2章介绍当前RDFS推理的相关工作;第3章研究RDFS推理,并给出Pregel[9]模型的相关概念;第4章描述基于消息传递机制的并行推理框架MPPIE;第5章为实验与分析;最后进行总结与展望。
2 相关工作
在众多推理的研究中,单机推理系统[10-11]可伸展性差,难以适应大规模RDF数据推理的需求,因此采用并行化方法解决推理问题已经成为一种趋势。目前的并行推理研究主要分为以下3类:
(1)闭包计算推理
闭包计算推理是指计算所有隐含信息。Weaver 与Hendler[3]利用MPI(message passing interface)并行技术,将推理任务划分成多个独立子任务,每个物理节点均保存一份完整的模式数据,最后合并各个节点上的推理结果,但该技术会产生大量重复数据。基于MapReduce技术,WebPIE[4]的推理过程由多个Map和Reduce操作组成,通过规则间的依赖关系,完成推理计算,是目前开源性能最好的并行推理引擎。Liu等人[5]将WebPIE的工作扩展到模糊pD规则推理之中,其效果与WebPIE相当。顾荣等人[12]基于MapReduce实现高效可扩展的语义推理引擎。在新型硬件的基础上,文献[6]利用共享内存体系结构,实现了RDFS推理,但可扩展性受到机器核数的限制。Peters等人[7-8]利用Rete[13]算法实现了语义推理,但通信代价较高。文献[14]利用分布式哈希表进行推理,然而无法有效处理大规模数据,可扩展性较差。此外,Oren等人[15]基于数据划分提出了divide-conquerswap策略,实现了Marvin,但其性能取决于输入数据规模。文献[16]使用规则集[17]实现了增量式推理,然而可扩展性受限于机器核数。
(2)查询时推理
查询时推理仅根据给定查询推理出与查询相关的隐含三元组。Kaoudi等人[18]在分布式哈希表的基础上,完成前向链接推理与反向链接推理的实现与对比,以查询驱动反向链接推理,但存在负载均衡问题。Salvadores等人[19]研究了RDFS的反向链接推理,以分布式存储系统4store为基础,将MRDF规则[20]推理形式化,并进行性能以及可伸展性测试,但是实现规则集较简单。文献[21]在查询过程中融入RDFS推理,查询重写将在扫描处理该查询必需的文件时进行,根据重写后的查询,扫描所有与之相关的三元组数据,然而该方法仅实现了subClass规则。
(3)混合推理
一些研究工作充分利用上述两者的优势,提出混合式推理方案。QueryPIE[22]分析了前向链接与反向链接推理的优缺点,提出了一种混合推理方法:首先在查询前完成模式数据的推理,以此减少查询中的重复计算;然后利用提前推理的结果对推理树进行剪枝,避免多余计算。Rya[23]基于Apache Accumulo完成了混合推理,但实现规则较少。
值得注意的是,各类研究适用于不同情况。本文属于闭包计算推理,与其他两类不具可比性。利用RDF数据的图结构,将推理过程映射为在图上两个顶点之间添加新边的过程,提出了一种新的基于消息传递机制的并行推理框架,以RDF图中的顶点为计算单元,执行推理操作。
3 基本概念
RDF是W3C提出的标准数据表示格式,能够将语义Web中的信息表达成机器理解的语义信息。
定义1(RDF三元组t)一条RDF三元组t由主语s、谓语p、宾语o组成,表示成:
t=(s,p,o)∈U⋃B×U⋃B×U⋃B⋃L
其中U、B和L分别为统一资源标识符(uniform resource identifier,URI)的集合、匿名节点的集合以及字面值的集合。主语集合、谓语集合以及宾语集合分别由S、P、O表示。
定义2(RDF图G)有限条三元组t的集合构成RDF图G={t|t∈S×P×O}。其中,G映射到图结构上的顶点集合为V={v|v∈S⋃O},边的集合为E= {e|e=
G是一种具有语义的特殊的有向标签图。某些三元组的谓语可作为其他三元组的主语或宾语出现,即V⋂P≠∅。图形上表现为允许边作为顶点出现,在数学上将这种图称为3-均匀超图。
下面将介绍RDFS推理规则以及Pregel计算模型。本文方法正是在Pregel模型的基础上实现了RDFS推理。
3.1RDFS推理规则
RDFS提供了RDF数据的数据模型定义,扩展了基本的RDF词汇,描述了类和属性之间的关系。RDFS规则集被证明是完备的[24],是推理研究中首选的规则集。表1中所列的规则集用R表示。
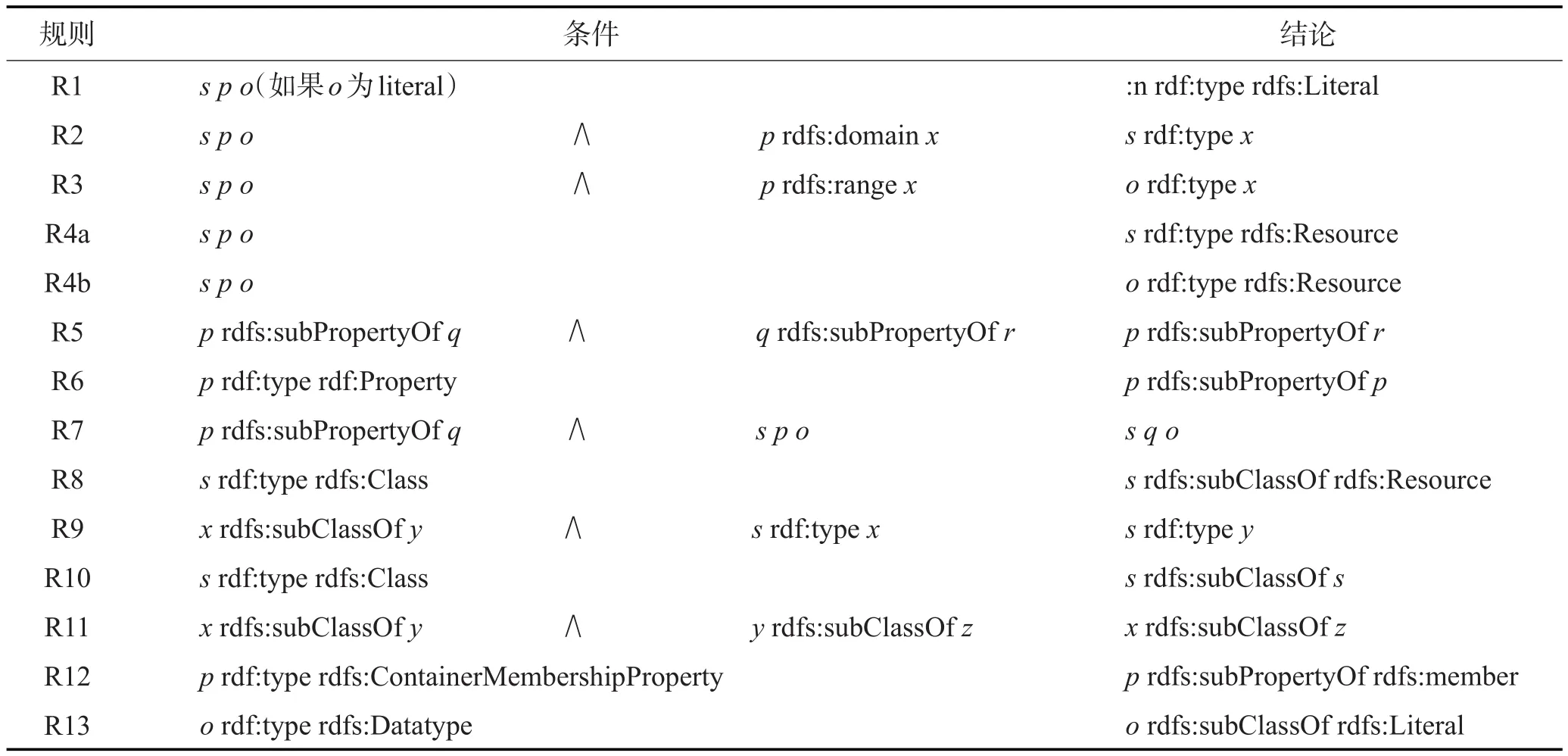
Table 1 RDFS inference rules表1 RDFS推理规则集
RDFS规则集中的R1、R4a与R4b表示每个三元组中的主语与宾语为字面值或者资源,对推理并无实际意义,因此不进行讨论。为了简洁起见,后文将使用表2中谓语的缩写形式。

Table 2 Abbreviation for predicates of RDFS rules表2 RDFS规则集中谓语的缩写形式
定义3(推理)给定RDF图G与规则集R,根据R中的某条规则ri得到G中蕴含的三元组集合T的过程称为推理过程,记作G├riT。
定义4(RDF图的推理闭包G*)给定RDF图G与完备的规则集R,G*为G的推理闭包,那么G*=Gα当且仅当Gα=Gα-1,其中Gα满足:
(1)G0=G
(2)Gα=Gα-1⋃{t|Gα-1├riT,t∈T,ri∈R}
当RDF图通过迭代应用推理规则得到推理闭包时,推理工作结束。所得到的推理闭包G*为最终包含所有隐含信息的RDF图。
3.2Pregel计算模型
Google为了处理大规模图计算领域中的问题,提出了一种基于整体同步并行(bulk synchronous parallel,BSP)[25]的分布式图计算模型Pregel,能够有效地解决大规模图计算问题。
定义5(Pregel计算模型)整个计算过程由一系列称之为超步(superstep)的迭代步骤组成,以顶点为中心进行计算,计算由消息驱动。Pregel模型中部分核心操作符的定义如下:
(1)输入数据图G。Idv表示顶点V的标识符集合。对∀v∈V,定义映射:
①id:V→Idv,返回v的唯一标识符;
②inEdges:V→E,返回v的入边集合;
③outEdges:V→E,返回v的出边集合。
对∀e∈E,定义:
①p:E→P,返回e上的谓语;
②srcId:E→Idv,返回e的源顶点;
③dstId:E→Idv,返回e的目的顶点。
(2)并行操作。∀v∈V,v存在活跃与停机两种状态。在每个超步中,活跃状态顶点并行执行用户定义的Compute方法。在每个v上定义如下函数:
①getSuperstep(),获取当前超步次序;
②voteToHalt(),将顶点状态置为停机;
③sendMessage(vid,message),将message发送给顶点id为vid的顶点;
④addEdge(e),将边e添加到图上。
如图1所示,白色顶点代表活跃状态顶点,灰色顶点代表停机状态顶点。

Fig.1 Pregel computation model图1 Pregel计算模型
每一个接收到消息的活跃状态顶点将执行一次Compute方法。该方法接收来自前一个超步的消息集合M,完成相应的计算后,可发送消息给下一个超步中的某个计算顶点,也可进行停机操作。当所有顶点都已达到停机状态,且没有消息传递时,计算停止。
4 RDFS并行推理框架MPPIE
RDFS的推理过程是RDF图上迭代应用推理规则的过程,当RDF图中所有隐含信息都作为显式数据出现时,即在当前规则下,计算得到数据集的推理闭包时,迭代停止。定理1保证了由G能够得到G*。
定理1给定RDFS规则集R,由RDF图G可以得到G*。
证明由定义3可知,∀ri∈R有G├riT。因为G由有限条三元组构成,且RDFS规则集是完备的,根据定义4,那么必然∃α,使得Gα=Gα-1,其中G0=G,Gα=Gα-1⋃{t|Gα-1├riT,t∈T,ri∈R}。因此,在RDFS规则集R下,有G*=Gα。□
根据定理可知,RDFS推理计算是有限的。推理得到的G*为包含G中所有隐含三元组的RDF图。

Fig.2 An example for RDFS inference图2 RDFS推理示例
例1图2为RDFS推理示例。这里的RDF图来自于DBpedia数据集[26],其中非实线的边代表隐含的三元组。当所有非实线的边作为推理出的新边添加到该RDF图上时,即得到推理闭包。
4.1推理抽象模型
对于RDF图数据,MPPIE将推理过程抽象成在图上两个顶点之间添加新边的过程。执行推理时,各个规则的结论作为图上新边出现的形式有所差异。根据这些差异,将规则分为以下6类:
(1)R6、R10:仅一个条件,且生成边为一条从该顶点出发,指向自身的边。
(2)R8、R12、R13:仅一个条件,生成边为一条从该顶点出发,指向其他顶点的边。
(3)R5、R11:两个条件,具有传递性特点,且生成边的两个顶点由另一中间顶点相连。
(4)R7:两个条件,且生成边为已存在边的两个顶点间的新边。
(5)R2、R3:两个条件,且生成边的两个顶点分别为某一条边上其中一个顶点以及与边上谓语相邻边上的目的顶点。
(6)R9:两个条件,不具有传递性特点,且生成边的两个顶点由另一中间顶点相连。由于其不具备传递性特点,故与(3)进行了区分。
规则的不同特点决定了其在推理过程中需采用不同方式进行推理。通过以上分析,可将RDFS推理规则集抽象成6种不同的推理模型,如图3所示。其中虚线代表推理过程中产生的新边,即规则的结论。

Fig.3 Inference model图3 推理模型
在RDF图中,MPPIE将推理过程表示为不同推理模型的组合。
例2在图2中,(dbo:Actor, sc, ex:Artist)与(dbo: Artist, sc, ex:Person)满足推理模型3,得到(dbo:Actor, sc, ex:Person)。
4.2规则执行顺序优化
在RDFS规则集的条件和结论中,三元组类型可为任意实例三元组,或以type、sc、sp、dom和ran为谓语的三元组。当某条规则结论的三元组类型恰好与另一条规则条件中某一三元组类型相一致时,前一规则的结论可作为后一规则的条件。例如,R2的结论是以type为谓语的一条三元组,R9的条件包含以type为谓语的三元组以及以sc为谓语的三元组,那么R2的输出可作为R9的输入。
由图3的推理模型可以看出,前两类推理模型较简单,仅根据RDF图中的一条边,便可进行加边操作,完成推理。实现过程较简单,故不再讨论。对其余4类模型中的规则,依据条件与结论包含的三元组类型的不同,进一步进行如表3所示的分类。

Table 3 Classification of RDFS rules表3 RDFS推理规则分类
在表3中,“条件包含”或“结论包含”分别表示规则的条件或结论中至少有一条三元组满足该类型。同一行中结论包含的规则应在条件包含的规则之前执行,如第一行中,规则R7应在规则R2、R3之前执行。根据规则间的依赖关系,合理安排规则的执行顺序,可减少规则间的迭代,从而减少消息传递次数。MPPIE的规则执行顺序如图4所示。
定理2按照图4的规则执行顺序,所有规则执行一遍即可完成推理。
证明图4为有向无环图(directed acyclic graph,DAG),形成了一种拓扑序。在该拓扑序中,R9依赖于R2、R3和R11,R2与R3依赖于R7,同时R7依赖于R5。依据该拓扑序,执行一遍即可完成推理。□

Fig.4 Execution order of rules图4 规则执行顺序
4.3RDFS并行推理算法
MPPIE将RDF图上的每个顶点作为并行计算的单元,每个顶点通过消息传递进行通信,按照规则执行顺序完成推理过程。在初始超步中,分别判断邻边是否可以匹配某一推理模型。若匹配,则根据相应的推理模型添加新边。当加边操作完成后,如需进行下一步迭代,则将相关信息传递到下一轮超步计算中,否则将该顶点置为停机状态。当所有隐含信息均以新边形式建立在原RDF图上时,整个推理过程结束。最终得到的RDF推理闭包图即为结果图。
例3在图2中,该RDF图在超步0中,所有顶点都处于活跃状态,依据图4的规则执行顺序执行推理。例如顶点dbo:acting检测出邻边满足R5,将对应的目的顶点ex:involving的信息以消息的形式传递给需要添加新边的顶点dbo:staring。在下个超步中,dbo:staring接收到该消息,添加新边(dbo:staring, sp, ex:involving),并将状态置为停机。以此类推,当所有推理规则都执行完毕,推理结束。
下面对其余4类推理模型分别介绍其并行算法。
推理模型3传递闭包规则的推理
推理模型3包括sp以及sc传递规则。
算法1详细描述了传递闭包算法,主要步骤包括:
(1)对于所有处于活跃状态的顶点,判断入边与出边是否同时包含同一传递属性。若包含,向该入边的源顶点发送添加新边的消息,同时将状态置为停机。
(2)接收消息的顶点根据消息内容添加新边。此新边可作为下一轮推理中的条件,因此向此新边的目的顶点发送消息,使其变为活跃状态。
(3)重复执行以上两个步骤,直至所有顶点都达到停机状态。
例4图5展示了传递闭包规则sc的推理过程。传递属性链上共有3个顶点。在超步0时所有顶点处于活跃状态,只有顶点2同时满足入边与出边上包含sc属性,因此向需要添加新边的顶点1发送消息,激活下一超步中顶点1。在超步1时,顶点1添加新边(1,sc,3),并向顶点3发送消息。在超步2时,所有顶点没有新边需要添加,状态全部为停机,传递闭包推理结束。
算法1传递闭包算法Compute(M)
输入:消息集合M
输出:是否停机
1. curStep¬getSuperstep();
2. If curStep = 0 then
3. For∀ei∈v.inEdges,∀eo∈v.outEdges do //tranP同为sc或sp
4.If ei.p =tranP and eo.p = tranP then
5.sendMessage (ei.srcId , Message (eo.dstId) ;
6.End if
7. End for
8. Else if curStep % 2 = 1 then //奇数次超步,加边
9. For∀m∈M do
10.创建新边e;
11.e.srcId←v.id,e.srcId←m.vid,e.p←tranP ;
12.v.addEdge(e) ; //添加新边
13.sendMessage(e.dstId, Message(v.id)) ;
14.End for

Fig.5 An example for transitivity closure图5 传递闭包示例
15. Else //偶数次超步,确定新边信息,并发送消息
16. For∀m∈M do
17. For∀eo∈v.outEdges do
18. If eo.p = tranP then
19.sendMessage(m.vid, Message (eo.dstId)) ;
20. End if
21. End for
22. End for
23. End if
24. voteToHalt();
算法1中两次迭代完成一次加边过程:第一次迭代确定加边信息,并把相关信息发送给需要加边的顶点;第二次迭代根据接收到的加边信息,完成加边。

个超步能够完成传递闭包推理计算。

第k次进行添加新边操作时,所有新边集合中边的最长距离为2k。此类新边的目的顶点称为边缘顶点。所有以此类新边的源点为起始点的新边集合中,若包含新边距离小于2k的新边,向这些新边的目的顶点发送的消息为多余的消息。因此,在算法1中,仅需向边缘顶点发送消息。在第11行前添加:If 2curStep= e.step进行判断,其中以e.step表示两点之间的路径长度。该优化策略可减少不必要的消息传递。
推理模型4 sp继承规则的推理
算法2为sp继承算法。活跃顶点判断出边属性是否有父属性,若存在父属性,则以父属性作为新边的谓语,完成对应的加边操作。
算法2 sp继承算法Compute(M)
输入:消息集合M
输出:是否停机
1. For∀eo∈v.outEdges do
2. If eo.p∈subP.srcIds then //subP存储p为sp的边
3.For∀d∈subP.dstIds do
4.创建新边e;
5.e.srcId←v.id,e.dstId←eo.dstId,e.p←d ;
6.v.addEdge(e) ;
7.End for
8.End if
9. End for
10. voteToHalt();
该算法在一轮迭代中即可完成sp继承规则的推理。假设该顶点有N条出边的属性存在父属性,且其中父属性平均个数为K个,那么该算法的时间复杂度为O(N×K)。
例5如图2所示,(db:Rain_Man, dbo:staring, db: Tom_Cruise)与(dbo:staring, sp, ex:acting),(db:Rain_ Man, dbo:acting, db:Tom_Cruise)与(dbo:acting, sp, ex: involving)满足推理模型4,根据算法2的计算过程,得到(db:Rain_Man, ex:acting, db:Tom_Cruise)与(db: Rain_Man, ex:involving, db:Tom_Cruise)。
推理模型5类型规则的推理
推理模型5包括dom以及ran类型规则。
算法3为类型推理算法。活跃顶点分别判断出边属性上是否包含定义域以及入边属性上是否包含值域,若满足其中之一,则添加对应的新边信息。
算法3类型推理算法Compute(M)
输入:消息集合M
输出:是否停机
1. curStep¬getSuperstep();
2. If curStep = 0 then
3. For∀eo∈v.outEdges do
4. If eo.p∈domain.srcIdsthen//domain存储p为dom的边
5.For∀d∈domain.dstIds do //R2添加新边操作
6.创建新边e;
7.e.srcId←v.id,e.dstId←d,e.p←type ;
8.v.addEdge(e) ;
9.End for
10.End if
11. End for
12. For∀ei∈v.inEdges do
13. If ei.p∈range.srcIds then //range存储p为ran的边
14.For∀d∈range.dstIds do //R3添加新边操作
15.创建新边e;
16.e.srcId←v.id,e.dstId←d,e.p←type ;
17.v.addEdge(e) ;
18.End for
19.End if
20. End for
21. End if
22. voteToHalt();
该算法在一轮迭代中即可完成新边的添加,仅判断边上的属性是否包含定义域或者值域。假设该顶点包含定义域的属性个数平均为d个,且有K个定义域,包含值域的属性个数平均为h个,且有N个值域,那么该算法的时间复杂度为O(d×K+h×N)。
例6如图2所示,(db:Rain_Man, dbo:staring, db: Tom_Cruise)与(dbo:staring, dom, dbo:Film),(db:Rain_ Man, ex:involving, db:Tom_Cruise)与(dbo: involving, dom, dbo:Work),(db:Rain_Man, dbo:staring, db:Tom_ Cruise)与(dbo:staring, ran, dbo:Actor),(db:Rain_Man, ex:involving, db:Tom_Cruise)与(dbo: involving, ran, dbo:Person)满足推理模型5,根据算法3的计算过程,得到(db:Rain_Man, type, dbo:Film)、(db:Rain_Man, type, dbo:Work)、(db:Tom_Cruise, type, dbo:Actor)以及(db:Tom_Cruise, type, dbo:Person)。
推理模型6 sc继承规则的推理
算法4为sc继承算法。活跃顶点判断出边中的属性是否包含sc,同时入边中的属性是否包含type,如两者同时满足,则完成对应的添加新边的操作。
算法4 sc继承算法Compute(M)
输入:消息集合M
输出:是否停机
1. curStep¬getSuperstep();
2. If curStep = 0 then
3. For∀ei∈v.inEdges,∀eo∈v.outEdges do
4.If ei.p = type and eo.p = sc then
5.sendMessage (ei.srcId , Message (eo.dstId )) ;
6.End if
7.End for
8. Else //接收到新边信息,进行加边操作
9.For∀m∈M do
10.创建新边e;
11.e.srcId←v.id,e.dstId←m.vid,e.p←type ;
12.v.addEdge(e);
13.End for
14. End if
15. voteToHalt();
假设该顶点共有K条入边和N条出边,则超步0的时间复杂度为O(K×N)。在K条入边中,假设有k条边的谓语为type,在N条出边中有n条边的谓语为sc,则共会发送k×n条消息。在超步1的时间复杂度为O(k×n)。因此,该算法的时间复杂度为O(K×N+k×n)。
例7如图2所示,(db:Tom_Cruise, type, dbo:Actor) 与(dbo:Actor, sc, dbo:Artist)满足推理模型6,根据算法4的计算过程,由顶点dbo:Actor发送消息到顶点db:Tom_Cruise。db:Tom_Cruise接收到消息后,添加新边(db:Tom_Cruise, type, dbo:Artist)。
下面对MPPIE并行推理算法的正确性进行证明。
定理4给定RDF图G以及RDFS规则集R,由以上算法可得到G*。
证明首先证明算法的可靠性(归纳法)。
归纳基础。第1次推理添加新边时,根据以上算法,仅有满足规则的条件才能得到相应的结论。该结论作为新边加入到G中,即满足∀ri∈R,G├riT推理结果可靠,此时G1=G⋃{t|G├riT,t∈T,ri∈R}。
归纳步骤。假设第k次推理过程中,∀ri∈R有Gk=Gk-1⋃{t|Gk-1├riT,t∈T,ri∈R},且Gk-1├riT的推理结果可靠。当第k+1次添加新边时,根据以上算法,以Gk作为输入数据图。当满足规则的条件时,添加相应的结论,那么有Gk├riT的推理结果是可靠的,此时Gk+1=Gk⋃{t|Gk├riT,t∈T,ri∈R}。由假设可知,前k次推理结果可靠,那么第k+1次推理结果可靠。
其次证明算法的完备性(反证法)。
假设由所提出的算法推理得到的结果集合为EM,t∈G*但t∉EM。若t∈G*,由定义4可知,t必为某一规则的结论。同时,按照图4的规则执行顺序进行推理时,t可由推理规则推出,即t∈EM。而假设为t∉EM,矛盾。因此得证。□
5 实验
基于开源框架Apache Giraph实现了MPPIE。Giraph是Pregel计算模型的实现,底层为Hadoop (http://hadoop.apache.org/)框架,通过消息驱动顶点完成计算。本文与WebPIE进行对比实验。
5.1实验环境与数据集
实验集群由8台节点构成,由一台Gigabit以太网交换机连接。每个计算节点配置为Intel®Xeon®CPU E5 @ 2.00 GHz,内存为64 GB,并配置1 TB硬盘。操作系统为64位Ubuntu 12.04 LTS Server,Giraph版本1.1.0,Hadoop版本0.20.203。
实验选用标准数据集LUBM(Lehigh University Benchmark)[27]和真实数据集DBpedia 3.9进行测试。MPPIE采用与WebPIE相同的数据编码方案。所有测试数据经过压缩编码后,均匀分布在各个计算节点上。
LUBM作为标准语义知识库,已经成为大规模语义应用的测试基准。以随机的形式生成某大学部门、教师以及学生等数据信息。本实验生成5组规模不同的LUBM数据集:LUBM- 200、LUBM- 400、LUBM-600、LUBM-800和LUBM-1000,分别代表了200、400、600、800和1 000个大学的数据,三元组条数从27.64×106到138.32×106不等。
DBpedia是从维基百科中抽取出的结构化信息数据,被广泛应用在语义Web领域相关应用的实验测试之中。本实验选取了DBpedia的部分数据,分别为:instance_types_en、mappingbased_properties_en和specific_mappingbased_properties_en数据集。其三元组规模达到42.53×106条。
表4为所选用实验数据集的详细信息。
5.2实验结果及分析
所有实验均使用了完整的RDFS规则集作为推理规则集,所有实验结果均为平均值。首先,在LUBM数据集和DBpedia数据集上测试并对比了MPPIE与WebPIE的推理执行性能。其次,测试了不同规模的LUBM数据集对推理性能的影响。最后,进行了集群可伸展性实验,设计了在1到8个节点规模的集群下MPPIE与WebPIE性能变化实验。
5.2.1执行性能测试与对比
在6组数据上测试并对比MPPIE与WebPIE执行性能,各自推理执行时间如表5所示。

Table 4 Information of datasets表4 数据集统计信息

Table 5 Comparison of reasoning time表5 推理执行时间对比
MPPIE推理时间在14.37 s到41.78 s之间。实验结果表明,相比WebPIE,MPPIE的推理执行速度快一个数量级以上。MPPIE的效率明显高于基于Map-Reduce的推理工作的执行效率,其原因分析如下:(1)采用的消息传递机制更适合于图上的推理工作;(2)以顶点为中心进行计算,充分考虑了RDF图数据的结构特点;(3)由推理得到的结果作为图上的新边存储时,若该边在图中已经存在,则不再重复添加,减少了重复数据处理过程。
5.2.2数据规模对推理性能的影响
选取从200到1 000个大学规模不等的LUBM数据集进行数据可伸展性测试。图6展示了MPPIE与WebPIE各自的推理执行时间。

Fig.6 Scalability test using datasets with different scale图6 不同规模数据集对推理性能的影响测试
实验结果表明,随着LUBM数据集规模的增大,MPPIE推理时间与数据集规模基本呈线性增长趋势。
在每个数据集上,WebPIE推理执行时间均明显高于MPPIE。取两者的比值作为评价MPPIE相比于WebPIE执行速度快慢的标准,该值表示执行速度提升的倍数,比值越大,说明MPPIE性能越好。图7展示了在不同规模数据集上,MPPIE执行速度相比于WebPIE提升的倍数变化趋势。

Fig.7 Multiples of reasoning speed图7 推理执行速度提升倍数
随着LUBM数据集规模不断增大,MPPIE执行速度提升的倍数呈现下降趋势,但其下降趋势逐渐平缓。主要由于在推理过程中,各个集群节点上消息传递的通信代价随着推理数据规模增大而有所增加,导致推理速度提升的倍数呈下降趋势。根据此趋势,预测推理速度提升的倍数可能达到某个阈值,且至少较WebPIE高一个数量级。
在LUBM数据集上,平均提升倍数为38.26倍,在DBpedia数据集上,平均提升倍数为30.23倍。整体平均提升倍数为34.25倍。
此外,推理过程中的吞吐率是衡量推理性能的主要指标,表示单位时间内推理出的三元组条数。对于不同的数据集,MPPIE推理平均吞吐率如图8所示。

Fig.8 Average throughput of reasoning图8 推理的平均吞吐率
实验结果显示,在LUBM数据集上,随着数据规模的不断增大,吞吐率逐渐上升,最高可以达到798.23 KTriples/s。而在DBpedia数据集上,其隐含的三元组条数与LUBM-200相近,但吞吐率小于LUBM-200的吞吐率。分析DBpedia与LUBM数据集的特点可知,相比于标准数据集LUBM,真实数据集DBpedia的复杂度较高,实验结果说明数据集的复杂度会影响推理过程中的吞吐率。
5.2.3集群规模对推理性能的影响
集群规模从1个节点逐渐增加到8个节点,对MPPIE的推理性能变化进行了评估。数据集选用真实数据集DBpedia和标准数据集LUBM-1000。集群规模对推理性能影响的实验结果如图9所示。
在DBpedia与LUBM-1000数据集上,图9中(a)与(b)的实验结果均显示,随着集群规模的增大,MPPIE推理执行时间迅速下降。当集群规模不断增大时,由于集群中各个节点之间的通信代价会逐渐增加,致使并行推理计算的时间逐渐趋近某个极限阈值。同时,图9显示,在1至8个节点的集群上,MPPIE达到极限阈值的速度慢于WebPIE,说明其可伸展性优于WebPIE。

Fig.9 Scalability test using clusters with different scales图9 不同规模集群上可伸展性测试
随着集群规模的增大,消息传递的代价将会增加并趋于平缓,下面讨论消息传递的复杂度。
假设推理过程中需发送的消息总数为M。当在单节点上进行推理时,消息的传递无需通过节点间的通信来完成,节点之间的通信代价为0。设集群中有n个节点,数据均匀分布在这n个节点上。假设传递某条消息的两个顶点位于不同的节点,该消息传递所带来的节点间的通信代价为δ。随着n的增大,数据分布将会更加分散,传递消息的两个顶点位于不同节点上的可能性增大。最坏情况下,M条消息均需跨节点传递,那么由消息传递所带来的通信代价为M×δ。即随着集群增大到某一值,由消息传递所带来的通信代价达到极限,其最坏复杂度为O(M×δ)。
取单节点与多节点推理执行时间的比值作为该多节点推理计算的相对加速比,该值可表示集群规模对推理性能的影响程度。随着集群规模的增大相对加速化的变化趋势趋于平缓,说明计算性能已达到极限。MPPIE与WebPIE的相对加速比变化趋势如图10所示。

Fig.10 Relative speedup in clusters with different scales图10 不同规模集群上的相对加速比
当集群规模由1个节点增长到8个节点时,在DBpedia数据集上,MPPIE的相对加速比增加到5.72。在LUBM-1000数据集上,MPPIE的相对加速比增加到9.48。而WebPIE的相对加速比并不是很明显,并在大于4个节点的集群上,相对加速比达到极限。实验结果表明,MPPIE具有良好的可伸展性,且明显优于WebPIE。
5.3与YARM工作的性能比较
文献[12]提出的YARM(yet another reasoning system with MapReduce)是基于MapReduce实现的语义推理工作,其性能相比于其他基于MapReduce的工作有明显提高。实验结果表明YARM实验性能相比于Reasoning-Hadoop[28]提高10倍左右。Reasoning-Hadoop与WebPIE同为Urbani等人的工作,不同的是WebPIE将Reasoning-Hadoop的工作扩充到OWL Horst规则集上。在实验中,仅选用WebPIE的RDFS推理部分进行实验对比。因此,文献[12]所对比的Reasoning-Hadoop与MPPIE选用的WebPIE为同一工作。实验结果表明,MPPIE相比于WebPIE平均快30倍以上。文献[12]集群采用1个主控制节点,16个计算节点,且单节点性能优于本工作所用集群中的单节点性能。但无论集群规模多大,并行计算的性能提升倍数理论上是与硬件配置无关的。显然,如果在相同的硬件上,MPPIE平均会比YARM快3倍左右。
6 总结与展望
RDF图数据本身的特点决定了其更适合于在基于消息传递机制的图计算框架下进行处理,本文基于消息传递机制提出了一种新的RDFS并行推理框架MPPIE。将RDFS推理规则的推理过程映射为图上两个顶点之间添加新边的过程,并根据不同的加边特点,抽象出不同的推理模型。推理过程中,以RDF图上的每个顶点为独立计算的单元,通过消息驱动顶点完成推理计算。标准数据集和真实数据集上的实验结果表明,MPPIE推理执行速度较WebPIE 快25倍以上,最高可达58倍。实验数据显示,MPPIE可伸展性明显优于WebPIE。
下一步工作将从以下两个角度展开:(1)减少消息传递,如优化并行计算过程,采取更优的模式数据与实例数据的存储划分方案等。(2)目前的工作仅考虑了RDFS推理规则集,在未来的工作中,将扩展到OWL等表达能力更丰富的规则集中。
References:
[1] Schmachtenberg M, Bizer C, Paulheim H. Adoption of the linked data best practices in different topical domains[C]// LNCS 8796: Proceedings of the 13th International Semantic Web Conference, Riva del Garda, Italy, Oct 19-23, 2014. Cham, Switzerland: Springer International Publishing, 2014: 245-260.
[2] Kaoudi Z, Manolescu I. RDF in the clouds: a survey[J]. The VLDB Journal, 2015, 24(1): 67-91.
[3] Weaver J, Hendler J. Parallel materialization of the finite RDFS closure for hundreds of millions of triples[C]//LNCS 5823: Proceedings of the 8th International Semantic Web Conference, Chantilly, USA, Oct 25-29, 2009. Berlin, Heidelberg: Springer, 2009: 682-697.
[4] Urbani J, Kotoulas S, Maassen J, et al. OWL reasoning with WebPIE: calculating the closure of 100 billion triples[C]// LNCS 6088: Proceedings of the 7th Extended Semantic Web Conference, Heraklion, Greece, May 30-Jun 3, 2010. Berlin, Heidelberg: Springer, 2010: 213-227.
[5] Liu Chang, Qi Guilin, Wang Haofen, et al. Large scale fuzzy pD*reasoning using MapReduce[C]//LNCS 7031: Proceedings of the 10th International Semantic Web Conference, Bonn, Germany, Oct 23- 27, 2011. Berlin, Heidelberg: Springer, 2011: 405-420.
[6] Heino N, Pan J Z. RDFS reasoning on massively parallel hardware[C]//LNCS 7649: Proceedings of the 11th International Semantic Web Conference, Boston, USA, Nov 11-15, 2012. Berlin, Heidelberg: Springer, 2012: 133-148.
[7] Peters M, Brink C, Sachweh S, et al. Rule-based reasoning on massively parallel hardware[C]//Proceedings of the 9th International Workshop on Scalable Semantic Web Knowledge Base Systems, Sydney,Australia, Oct 21, 2013: 33-49.
[8] Peters M, Brink C, Sachweh S, et al. Scaling parallel rulebased reasoning[C]//LNCS 8465: Proceedings of the 11th Extended Semantic Web Conference, Anissaras, Greece, May 25-29, 2014. Cham, Switzerland: Springer InternationalPublishing, 2014: 270-285.
[9] Malewicz G, Austern M H, Bik A J C, et al. Pregel: a system for large-scale graph processing[C]//Proceedings of the 2010 ACM SIGMOD International Conference on Management of Data, Indianapolis, USA, Jun 6-11, 2010. New York, USA:ACM, 2010: 135-146.
[10] Broekstra J, Kampman A, van Harmelen F. Sesame: a generic architecture for storing and querying RDF and RDF schema [C]//LNCS 2342: Proceedings of the 1th International Semantic Web Conference, Sardinia, Italy, Jun 9- 12, 2002. Berlin, Heidelberg: Springer, 2002: 54-68.
[11] Wilkinson K, Sayers C, Kuno H A, et al. Efficient RDF storage and retrieval in Jena2[C]//Proceedings of the 1st International Workshop on Semantic Web and Databases, Berlin, Germany, Sep 7-8, 2003. Berlin, Heidelberg: Springer, 2003: 131-150.
[12] Gu Rong, Wang Fangfang, Yuan Chunfeng, et al. YARM: efficient and scalable semantic reasoning engine based on MapReduce[J]. Chinese Journal of Computers, 2015, 38(1): 74-85.
[13] Forgy C L. Rete: a fast algorithm for the many pattern/many object pattern match problem[J]. Artificial Intelligence, 1982, 19(1): 17-37.
[14] Fang Qiming, Zhao Ying, Yang Guangwen, et al. Scalable distributed ontology reasoning using DHT-based partitioning[C]// LNCS 5367: Proceedings of the 3rd Asian Semantic Web Conference, Bangkok, Thailand, Dec 8- 11, 2008. Berlin, Heidelberg: Springer, 2008: 91-105.
[15] Oren E, Kotoulas S, Anadiotis G, et al. Marvin: distributed reasoning over large-scale semantic Web data[J]. Web Semantics: Science, Services and Agents on the World Wide Web, 2009, 7(4): 305-316.
[16] Urbani J, Margara A, Jacobs C, et al. Dynamite: parallel materialization of dynamic RDF data[C]//LNCS 8218: Proceedings of the 12th International Semantic Web Conference, Sydney, Australia, Oct 21- 25, 2013. Berlin, Heidelberg: Springer, 2013: 657-672.
[17] Munoz S, Pérez J, Gutierrez C. Minimal deductive systems for RDF[C]//LNCS 4519: Proceedings of the 4th European Semantic Web Conference, Innsbruck, Austria, Jun 3-7, 2007. Berlin, Heidelberg: Springer, 2007: 53-67.
[18] Kaoudi Z, Miliaraki I, Koubarakis M. RDFS reasoning and query answering on top of DHTs[C]//LNCS 5318: Proceedings of the 7th International Semantic Web Conference, Karlsruhe, Germany, Oct 26-30, 2008. Berlin, Heidelberg: Springer, 2008: 499-516.
[19] Salvadores M, Correndo G, Harris S, et al. The design and implementation of minimal RDFS backward reasoning in 4store[C]//LNCS 6643: Proceedings of the 8th Extended Semantic Web Conference, Heraklion, Greece, May 29-Jun 2, 2011. Berlin, Heidelberg: Springer, 2011: 139-153.
[20] Muñoz S, Pérez J, Gutierrez C. Simple and efficient minimal RDFS[J]. Web Semantics: Science, Services and Agents on the World Wide Web, 2009, 7(3): 220-234.
[21] Husain M, McGlothlin J, Masud M M, et al. Heuristicsbased query processing for large RDF graphs using cloud computing[J]. IEEE Transactions on Knowledge and Data Engineering, 2011, 23(9): 1312-1327.
[22] Urbani J, van Harmelen F, Schlobach S, et al. QueryPIE: backward reasoning for OWL Horst over very large knowledge bases[C]//LNCS 7031: Proceedings of the 10th International Semantic Web Conference, Bonn, Germany, Oct 23-27, 2011. Berlin, Heidelberg: Springer, 2011: 730-745.
[23] Punnoose R, Crainiceanu A, Rapp D. Rya: a scalable RDF triple store for the clouds[C]//Proceedings of the 1st International Workshop on Cloud Intelligence, Istanbul, Turkey, Aug 31, 2012. New York, USA:ACM, 2012: 4.
[24] Hayes P. RDF semantics. W3C Recommendation, 2004.
[25] Valiant L G. A bridging model for parallel computation[J]. Communications of the ACM, 1990, 33(8): 103-111.
[26] Auer S, Bizer C, Kobilarov G, et al. DBpedia: a nucleus for a Web of open data[C]//LNCS 4825: Proceedings of the 6th International Semantic Web Conference, Busan, Korea, Nov 11-15, 2007. Berlin, Heidelberg: Springer, 2007: 722-735.
[27] Guo Yuanbo, Pan Zhengxiang, Heflin J. LUBM: a benchmark for OWL knowledge base systems[J]. Web Semantics: Science, Services and Agents on the World Wide Web, 2005, 3(2): 158-182.
[28] Urbani J, Kotoulas S, Oren E, et al. Scalable distributed reasoning using MapReduce[C]//Proceedings of the 8th International Semantic Web Conference, Chantilly, USA, Oct 21-25, 2009. Berlin, Heidelberg: Springer, 2009: 634-649.
附中文参考文献:
[12]顾荣,王芳芳,袁春风,等. YARM:基于MapReduce的高效可扩展的语义推理引擎[J].计算机学报, 2015, 38(1): 74-85.

LV Xiaoling was born in 1989. She is an M.S. candidate at Tianjin University, and the member of CCF. Her research interests include parallel inference and RDF data management.
吕小玲(1989—),女,河北唐山人,天津大学硕士研究生,CCF会员,主要研究领域为分布式推理计算,RDF数据管理。

WANG Xin was born in 1981. He received the Ph.D. degree from Nankai University in 2009. Now he is an associate professor at Tianjin University, and the senior member of CCF. His research interests include semantic Web data management, graph databases and large-scale knowledge processing.
王鑫(1981—),男,天津人,2009年于南开大学获得博士学位,现为天津大学副教授,CCF高级会员,主要研究领域为语义Web数据管理,图数据库,大规模知识处理。

FENG Zhiyong was born in 1965. He received the Ph.D. degree from Tianjin University in 1996. Now he is a professor and Ph.D. supervisor at Tianjin University, and the senior member of CCF. His research interests include knowledge engineering, service technology and security software engineering.
冯志勇(1965—),男,内蒙古呼和浩特人,1996年于天津大学获得博士学位,现为天津大学教授、博士生导师,CCF高级会员,主要研究领域为知识工程,服务技术,安全软件工程。

RAO Guozheng was born in 1977. He received the Ph.D. degree from Tianjin University in 2009. Now he is an associate professor at Tianjin University, and the member of CCF. His research interests include knowledge engineering and software engineering.
饶国政(1977—),男,湖北武穴人,2009年于天津大学获得博士学位,现为天津大学副教授,CCF会员,主要研究领域为知识工程,软件工程。

ZHANG Xiaowang was born in 1980. He received the Ph.D. degree from Peking University in 2011. Now he is an associate professor at Tianjin University, and the member of CCF. His research interests include artificial intelligence, databases and semantic Web.
张小旺(1980—),男,安徽池州人,2011年于北京大学获得博士学位,现为天津大学副教授,CCF会员,主要研究领域为人工智能,数据库,语义网。

XU Guangquan was born in 1979. He received the Ph.D. degree from Tianjin University in 2008. Now he is an associate professor at Tianjin University, and the senior member of CCF. His research interests include trusted computing, security and privacy.
许光全(1979—),男,湖南浏阳人,2008年于天津大学获得博士学位,现为天津大学计算机学院副教授,CCF高级会员,主要研究领域为可信计算,安全与隐私。
MPPIE: RDFS Parallel Inference Framework Based on Message Passingƽ
LVXiaoling1,2,WANG Xin1,2,3+, FENG Zhiyong1,2, RAO Guozheng1,2, ZHANG Xiaowang1,2, XU Guangquan1,2
1. School of Computer Science and Technology, Tianjin University, Tianjin 300072, China
2. Tianjin Key Laboratory of Cognitive Computing and Application, Tianjin 300072, China
3. General Data Technology Co., Ltd., Tianjin 300384, China
+ Corresponding author: E-mail: wangx@tju.edu.cn
LV Xiaoling, WANG Xin, FENG Zhiyong, et al. MPPIE: RDFS parallel inference framework based on message passing. Journal of Frontiers of Computer Science and Technology, 2016, 10(4): 451-465.
Abstract:Reasoning over semantic data poses a challenge, since large volumes of RDF (resource description framework) data have been published with the rapid development of the Semantic Web. This paper proposes an RDFS (RDF schema) parallel inference framework based on message passing mechanism. The graph structure of RDF data is exploited to abstract inference process to an edge addition model. Vertices execute the parallel inference algorithm, which can send reasoning messages to other vertices to complete inference process. When all derivations are regarded as new edges of initial RDF graph, the computation terminates. MPPIE (message passing parallel inference engine), the RDFS parallel inference framework, is implemented on top of open source framework Giraph. The experimental results on both benchmark dataset LUBM and real world dataset DBpedia show that the performance of the proposed method outperforms WebPIE, the state-of-art semantic scalable inference engine. Furthermore, the proposed method provides good scalability.
文献标志码:A
中图分类号:TP31
ddoi:10.3778/j.issn.1673-9418.1507072
