(k, q)阶分数差分方程的一个新解法

何　超，吴　正，王良龙

(安徽大学 数学科学学院，安徽 合肥 230601)



(k, q)阶分数差分方程的一个新解法

何超，吴正，王良龙

(安徽大学 数学科学学院，安徽 合肥 230601)

摘要：通过构造特殊函数Λ(-μ,λ)，利用待定系数法，给出(k, q)阶分数差分方程的一个新解法。

关键词：分数阶差分；分数阶和分；(k, q)阶分数差分方程

1695年Leibniz与L′ Hospital在通信中，首次探讨了传统微分中变元增量为非整数次幂时的相关极限问题，这标志着分数阶微分和分数阶微分方程的起源[1]。 后期的研究表明，分数阶微分和分数阶微分方程在物理、生物等学科研究中起着重要的作用[2-4]。Miller等[5]利用分数阶Green 函数、超越函数和Laplace方法，对分数阶常微分方程进行了较系统的研究，随后，在文献[6-7]中也提到了分数阶常微分方程的良好性质。

对于整数阶微分方程与整数阶差分方程，二者的许多性质都具有很好的可比性，那么能不能在目前的分数阶微分基础上，建立相应的分数阶差分理论呢？ 程金发[8]提出了一种全新的分数阶和分、分数阶差分以及分数阶差分方程定义，紧接又提出利用待定系数法求解(2,q)阶分数差分方程[9]，更进一步利用Z变换求解了(k, q)阶分数差分方程[10]。虽然待定系数法是一种浅显易懂的方法，但是在将其推广到(k, q)阶分数差分方程时，产生的尾项难以消除，迄今为止尚无完善的解决办法。本文通过选取不同的系数，构造一个类似范德蒙行列式，将待定系数法求解方程过程中产生的尾项消除，得到了待定系数法求解一类分数阶差分方程的通用方法。

首先引入文献[8]中的记号、定义及性质。

定义3定义(x)(n)x(x+1)(x+2)…(x+n-1)，这里n∈N+，x∈R，所定义的函数称之为上升阶乘函数；

定义5令m为超过μ>0 的最小正整数，则定义x(n)的μ阶分数差分为

μx(n)=m-(m-μ)x(n)。

定义6对于实数μ≥0，非零实数λ，正整数n，定义Λ(-μ,λ)=μλn,Λ(0,λ)=λn。

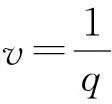
a1v+a00]x(n)=0

(1)

为一个(k,q)阶的分数阶差分方程,这里ai是常数，i=0,1,2,…,k-1且a0+a1+…+ak-1≠0。 称多项式p(x)=xk+ak-1xk-1+…+a1x+a0为 (1)式的特征多项式。

性质1对任意μ∈R，v>0，有μ-vx(n)=μ-vx(n)。

性质2设v>0，有

性质3对于v>0，μ∈R，有

(2)

接下来介绍两个引理：

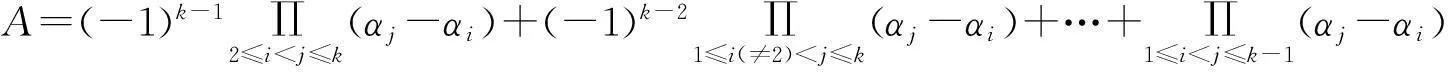
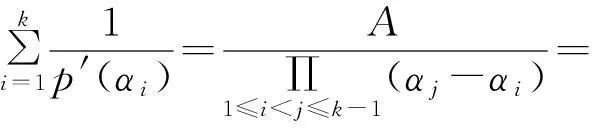
引理2设p(x)=0有k个单根，分别为α1,α2,…,αk，则

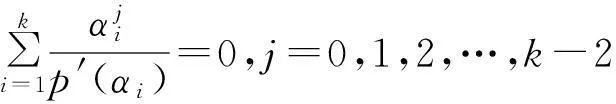
证明类似于引理1的证明，有

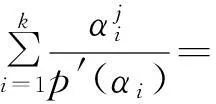
下面用待定系数法来证明定理1。

定理1[8]令p(x)=0有k个单根，分别为α1,α2,…,αk，则(1)式有解x(n)=

(3)

证明令x(n)=B0Λ(0,λ)+B1Λ(-v,λ)+…+Bq-1Λ[-(q-1)v,λ]为 (1)式的解，其中

Bi(i=0,1,…,q-1)与λ为任意常数。 由 (2) 式可得

B0Λ(-v,λ)+…+Bq-2Λ[-(q-1)v,λ]

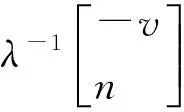
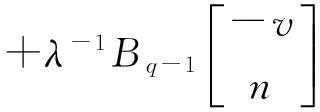
[(1-λ-1)Bq-k+ak-1(1-λ-1)Bq-(k-1)+…+

a1(1-λ-1)Bq-1+a0B0]Λ(0,λ)+[(1-λ-1)Bq-(k-1)+

ak-1(1-λ-1)Bq-(k-2)+…+a1B0+a0B1]Λ(-v,λ)+…+[(1-λ-1)Bq-1+ak-1B0+…+a1Bk-1+a0Bk]Λ(-kv,λ)+

(4)

因为α是p(λ)=0的根，有αk+ak-1αk-1+…+a1α+a0=0。 若α≠0，由Bj的任意性，不妨令

Bj=Aα-j，A∈R，则有

Bj+ak-1Bj+1+…+a1Bj+k+1+a0Bj+k=

Aα-j+ak-1Aα-j+1+…+α0Aα-(j+k)=

Aα-(j+k)(αk+ak-1αk-1+…+a1α+a0)=0,

此时(4)式右边可化为{(1-λ-1)Aα-(q-k)+ak-1(1-λ-1)Aα-[q-(k-1)]+…+a1(1-λ-1)Aα-(q-1)+a0A}Λ(0,λ)+{(1-λ-1)Aα-[q-(k-1)]+ak-1(1-λ-1)Aα-[q-(k-2)]+…+a1A+a0Aα-1}Λ(-v,λ)+

…+[(1-λ-1)Aα-(q-1)+ak-1A+…+a1Aα-(k-2)+

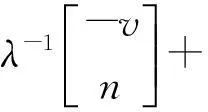
(5)

(6)

此时

(7)

(8)

由引理1和引理2得

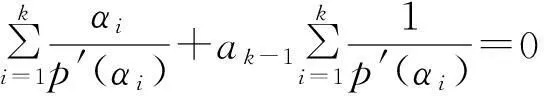
同理可得(8)式右边每一项的系数都为0，所以

参考文献:

[1] 郑祖庥. 分数微分方程的发展与应用[J].徐州师范大学学报 (自然科学版)，2008，26 (2)：1-10.

[2]F.Mainardi,R.Gorenflo.Onmittag-leffler-typefunctionsinfractionalevolutionprocesses[J].J.Comput.Appl.Math., 2000, 118: 283-299.

[3]V.Dartardar-Gejji,A.Babakhani.Analysisofasystemoffractionaldifferentialequations[J].J.Math.Anal.Appl., 2004, 293: 511-522.

[4]K.Diethelm,N.J.Ford.Multi-orderfractionaldifferentialequationsandtheirnumericalsolution[J].Appl.Math.Comput., 2004，154：621-640.

[5]K.S.Miller,B.Ross.AnIntroductiontotheFractionalCalculusandFractionalDifferentialEquations[M].NewYork：JohnWileyandSons, 1993.

[6]I.Podlubny.FractionalDifferentialEquations[M].SanDiego：AcadPress, 1999.

[7]A.A.Kilbas,H.M.Srivastava,J.J.Trujillo.TheoryandApplicationsofFractionalDifferentialEquations[M].Amsterdam:ElsevierScienceLtd., 2006.

[8] 程金发. 分数阶差分方程理论[M].厦门：厦门大学出版社，2011.

[9] 程金发，吴国春.(2，q)阶分数差分方程的解[J].数学学报，2012, 55 (3): 469-480.

[10] 程金发. 分数(k，q)阶差分方程的解[J].应用数学学报, 2011, 34 (3): 313-330.

New Method of Solving Fractional Difference Equation of Order (k, q)

HE Chao, WU Zheng, WANG Liang-long

(School of Mathematical Sciences，Anhui University，Hefei,Anhui 230601, China)

Abstract:This paper is concerned with the fractional difference equation of order (k, q). With constructing a special function Λ(-μ,λ), the expression of solution is obtained by the method of undetermined coefficients , which is a new method to solve the equation.

Key words:fractional difference, fractional summation, fractional difference equation of order (k, q)

文章编号：1007-4260(2016)01-0001-03

中图分类号：O175

文献标识码：A

DOI：10.13757/j.cnki.cn34-1150/n.2016.01.001

作者简介：何超，男，安徽芜湖人，安徽大学数学科学学院硕士研究生，主要研究方向为分数阶差分方程。E-mail: 1193451929@qq.com

基金项目：国家自然科学基金(10771001)，高等学校博士点基金(20113401110001)和安徽省自然科学基金(1308085MA01，1508085QA01)

*收稿日期：2015-07-15

网络出版时间：2016-03-15 17:05网络出版地址：http://www.cnki.net/kcms/detail/34.1150.N.20160315.1705.001.html