感应电机考虑铁耗的并联模型及对矢量控制的影响

李耀恒, 刁利军

(1. 北京交通大学电气工程学院, 北京 100044; 2. 北京市轨道交通电气工程技术研究中心, 北京 100044)

感应电机考虑铁耗的并联模型及对矢量控制的影响

李耀恒1, 刁利军2

(1. 北京交通大学电气工程学院, 北京 100044; 2. 北京市轨道交通电气工程技术研究中心, 北京 100044)

通过对感应电机铁耗电阻的分析，推导出静止两相坐标系下考虑铁耗的感应电机的并联等效电路，并建立了考虑铁耗的感应电机状态模型。与此同时建立并联方式下考虑铁耗的感应电机旋转坐标系下的等效电路，并在稳态时对其进行简化。在旋转坐标系下分析考虑铁耗对矢量控制的影响。通过Matlab/Simulink仿真，验证分析的正确性。依托混合动力动车组地面试验平台对理论分析进行验证，为进一步提升控制精度及深入研究异步电机最优磁链控制提供可靠依据。

感应电机； 铁耗； 矢量控制； 磁场定向

1 引言

4近年来，感应电机矢量控制已经得到国内外学者的深入研究，并且在实际工程中得到了广泛应用。然而由于受到分析方法和工具的限制，人们往往忽略铁耗的存在而只考虑铜耗电阻的影响。但是在实际的电机运行中，铁耗是真实存在的，并且对电机的效率产生较大影响。目前在该方面研究中存在两种等效方式，分别为铁耗电阻串联励磁支路模型和铁耗电阻并联励磁支路模型。进一步的研究表明，铁耗电阻串联励磁支路模型可推导出稳态转子d轴电流不为0的结论，不符合转子磁场定向矢量控制的基本原理，因而本文不再讨论串联等效电路，着重分析铁耗电阻并联等效电路。

由矢量控制的基本原理可知，感应电机运行过程中，铁耗的存在会使得电流和转子磁链相互干扰，造成电机在旋转坐标系下d-q轴解耦不彻底，使得磁场定向不准确，进而造成感应电机的效率忽高忽低，最终将影响整个系统的动、静态性能。因而，为了切实提高控制精度、优化电机运行效率，正确建立考虑铁耗的数学模型是很有必要的。

本文以感应电机定转子铁心损耗为基准，在建立了静止两相坐标系下感应电机考虑铁耗的等效电路的基础上，推导出考虑铁耗的感应电机状态模型。为验证模型的准确性，通过Matlab/Simulink仿真，对比考虑铁耗与忽略铁耗两种情况下，铁耗对电机矢量控制的影响。这一研究为提高矢量控制性能并为电机最优磁链控制提供了切实可靠的依据[1]。

2 静止坐标系下考虑铁耗的感应电机并联数学模型

电机的铁心由铁磁材料构成，铁磁材料在交变磁场作用下的反复磁化过程中，磁畴会不停转动，相互之间不断摩擦，因此会消耗一定的能量，从而产生功率损耗即磁滞损耗。

与此同时，对于硅钢片一类具有导电能力的铁磁材料，在交变磁场B的作用下，根据电磁感应定律，硅钢片中将有围绕磁通呈涡旋状的感应电动势和电流产生，即涡流；涡流在其流通路径上电阻中将会产生功率损耗，即涡流损耗。

正是由于磁滞损耗和涡流损耗的存在，励磁电流要超前磁通一个角度，因而励磁电流可认为产生两个分量，即有功分量和无功分量，其中无功分量用于励磁产生主磁通，有功分量用于产生铁耗，按照这种分解的思想，可以得到感应电机的铁耗并联数学模型，如图1所示[2]。

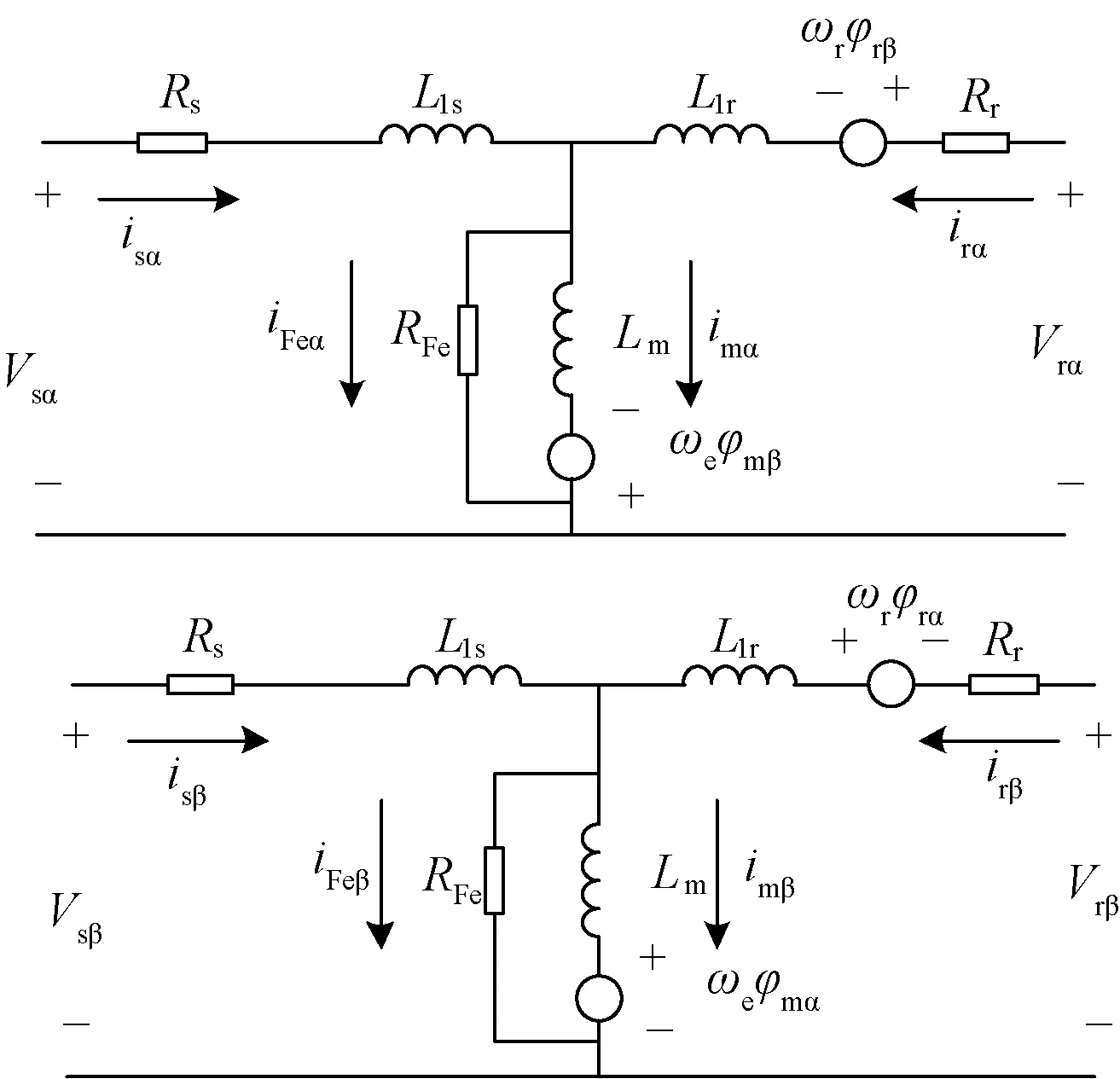
图1 静止坐标系下考虑铁耗的电机并联数学模型Fig.1 Mathematical parallel model under static coordinates considering iron loss of motor

由图1的感应电机等效电路，可以得到感应电机模型的磁链方程：

(1)

式中，φsα、φsβ、φrα、φrβ分别为定子及转子侧α、β轴磁链；isα、irα为定转子电流在α轴上的电流分量；isβ、irβ为定转子电流在β轴上的电流分量；iFeα、iFeβ为铁耗电阻支路在α、β轴上的电流分量；Lm为电机励磁电感；Lls、Llr为定转子侧漏感；φmα、φmβ为α、β轴上励磁电感所产生的磁场。

感应电机模型的电压方程如式(2)所示。

(2)

其中，Vsα、Vsβ为定子侧电压在α、β轴上的电压分量；Rs为电机定子电阻；Rr为电机转子电阻；ωr为电机转子转速。

忽略暂态过程，由式(2)可得用铁耗支路电流表示的转子电流：

(3)

其中，RFe为电机等效铁耗电阻；ωe为电机同步角速度。由转子磁链公式可得转子电流的另一个表达式：

(4)

其中，Lr为电机转子侧电感，其数值大小为励磁电感同转子侧漏感之和。将式(3)和式(4)两式对等，可推得铁耗支路电流表达式：

(5)

为简化表达式，可将铁耗支路电流用定子电流及转子磁链表示：

(6)

忽略电机漏感可得简化后的铁耗支路电流表达式：

(7)

为简化公式推导，在此定义：

将式(1)及式(2)的转子电流用式(4)替换，可得：

(8)

其中，s为微分因子。由式(8)可得转子磁链状态方程：

(9)

将转子磁链状态方程式(8)及铁耗支路电流方程式(5)，代入定子电压方程，可得定子电流状态方程：

(10)

定子电流状态方程及转子磁链状态方程构成考虑铁耗的感应电机并联数学模型，但是其形式过于复杂，不利于理论分析和工程应用。考虑到磁链和转速受到转子时间常数和机械时间常数限制而变化缓慢，因而铁耗支路电流iFeβ在一个控制周期内几乎保持不变；并且由于电机漏感较小，因而定子电流状态方程中的微分项系数约为0，故而可忽略其铁耗支路电流的微分项，则定子电流状态方程变为式(11)[3]。

(11)

将简化后的铁耗支路电流方程式(7)代入定子电流状态方程式(11)，并结合转子磁链状态方程式(9)可得考虑铁耗的感应电机并联数学模型方程式为式(12)。

(12)

其中

3 旋转坐标系下考虑铁耗的感应电机并联数学模型分析

本文第2节推导得出了静止坐标系下考虑铁耗的感应电机并联数学模型，但为了同控制方式相结合，选择在两相旋转坐标下进行感应电机动态及稳态工况下分析，两相d-q旋转坐标系下铁耗电阻并联励磁支路的感应电机等效电路如图2所示。

图2 旋转坐标系下考虑铁耗的电机并联数学模型Fig.2 Mathematical parallel model under rotating coordinate system considering iron loss of motor

两相旋转坐标系下的电机转子侧电压方程为：

(13)

其中，ωsl为电机的转差频率，稳态时，在转子磁场定向矢量控制系统中，倘若忽略定转子漏感，则：

(14)

由式(13)和式(14)可得：

(15)

稳态时，电机d-q旋转坐标系下电流可视为直流量，并且Lm压降为0，因而图2中的励磁回路方程为[4]：

(16)

由式(14)和式(16)可得两相旋转坐标系下铁耗支路电流表达式：

(17)

依据式(15)、式(17)并忽略定转子漏感，可将旋转坐标系下考虑铁耗的感应电机并联等效电路图简化，如图3所示。

图 3 旋转坐标系下考虑铁耗的电机简化等效电路Fig.3 Simplified equivalent circuit under rotating coordinate system considering iron loss of motor

依据简化后的考虑铁耗的电机简化等效电路图很明显可以看出，相比忽略铁耗的传统矢量控制，考虑铁耗的矢量控制在q轴下的影响较大，增加了铁耗支路电流分量，其对矢量控制的影响在第4节将详细论述。

4 铁耗对感应电机矢量控制的影响

传统矢量控制中只考虑铜耗，铁耗由于较小而被忽略，而用不考虑铁耗的矢量控制策略控制感应电机时，即使在电机参数辨识准确的情况下，实际的转子磁链同样会受到铁耗的影响，矢量控制器估算出的转子磁链同实际转子磁链相比存在偏差，并且由于存在

(18)

因而会进一步影响到对感应电机转差的估算，使得估算值同实际转差频率相比存在偏差[5]。

并且，铁耗会使运行中的电机转子电流和磁链相互干扰，导致d-q轴交叉耦合，这些交叉耦合依赖于转差频率，频率越高，交叉耦合含量越大。通常补偿的铁耗等值电阻为额定频率下的恒定值，不适用于变频调速领域，尤其在铁耗影响较大的高速区，因而相比传统矢量控制，铁耗对d-q轴的解耦影响较大，最终会导致磁链定向偏差[6]，其定向不准确(超前或滞后)对电机控制的影响分析如下。

图4 定向超前Fig.4 Orientation ahead

图5 定向滞后Fig.5 Orientation behind

根据以上分析，受铁耗电阻影响，电机磁链定向会非常不准确，最终造成定子电流的实际d轴、q轴分量不等于给定分量，矢量控制系统的磁通和转矩控制产生偏差[8]。

除此之外，如图3所示，旋转坐标系下考虑铁耗的电机等效电路中可明显看出，在q轴等效电路中存在铁耗支路，因而考虑了铁耗后，增加了定转子铁耗等效电阻中流过的电流iFe，并且这部分电流是定、转子铁耗等效电阻从定子电流中分得的，因而，考虑铁耗后，为保证输出功率恒定，电机要从输入侧获取更多的有功功率，来增加定子中的电流。这便意味着考虑电机铁耗时，电机的总电磁转矩的一部分要消耗在铁耗上。因此，考虑铁耗的感应电机转速动态响应变慢，并降低了电机动态响应性能[9]。

5 仿真及实验验证

混合动力动车组即为具有不同动力输入的动车组，有两种配置方式：一种是“25kV接触网供电+柴油发电机供电+锂电池供电”，简称DEMU；另一种是“25kV接触网供电+锂电池供电”，简称EEMU。牵引电机仿真参数采用国内首列混合动力动车组所采用的永济电机厂的牵引电机系数，如表1所示。

表1 牵引电机参数

依托混合动力动车组地面试验台，并采用以DSP TMS320F28335为控制核心的试验系统，对上述理论进行试验验证，电机参数同仿真参数一致，如表1所示，波形存储及设备试验电机分别如图6和图7所示。

图6 DL750录波仪Fig.6 DL750 wavecorder

图7 试验电机Fig.7 Test motor

实验过程中为实时观测转矩电流变化，通过DA芯片输出4～20mA电流的形式将转矩电流等比例输出，并经过电阻采样后接入示波器显示，试验波形如图8所示。图中上半部分时间轴为5s/格，下半部分时间轴为20ms/格。

图8 考虑铁耗后的矢量控制实验波形Fig.8 Experimental waveforms in vector control considering iron loss

为验证文中所推导的感应电机考虑铁耗的并联模型的稳定性，对其进行试验验证，实验波形如图8所示，采用速度环+转矩环+磁链环控制并加入铁耗补偿，电机从0加速至40Hz，稳定运行一定时间后从传统矢量控制模式下切换至接入铁耗补偿后的控制模式。从图中可以很明显看出，切换后转矩反馈电流在一定时间内没有实时跟踪上转矩指令电流，但在后期跟踪良好，究其原因，为铁耗电阻对磁场的建立过程有较大影响反映到电机外特性上则表现为启动阶段的转矩建立较慢，同上文理论分析一致。

为了保证忽略铁耗的感应电机模型和考虑铁耗的感应电机模型对比的有效性，首先采用V/F控制模式，给予同样的频率指令84Hz，在相同脉冲下对两者的动态响应性能进行比较，其波形如图9所示。

图9 VF模式下两种模型速度对比Fig.9 Two models velocity contrast in VF mode

可以看出，在相同频率指令下，与忽略铁耗的感应电动机模型相比较，考虑铁耗的感应电动机模型动态响应较慢，但是在此模式下考虑铁耗后并不会影响电机转速的终值，如放大图所示二者的速度终值相同，其差异体现在动态响应性能方面。究其原因，铁耗电阻主要影响转子磁链的惯性时间常数，从而对转矩的动态性能产生影响[10]，反映在电机外特性上则表现为启动阶段的转矩建立较慢，所以考虑铁耗的动态响应性能要比忽略铁耗的慢些。

6 结论

本文由感应电机的基本特性推导出感应电机考虑铁耗电阻的并联等效电路，并根据等效电路得出其数学模型；以此为基础，剖析电机运行过程中考虑铁耗电阻对感应电机矢量控制的影响，并通过仿真及实验波形验证其准确性，为后续最优磁链控制的研究提供了理论基础。

[1] 辜承林(Gu Chenglin).电机学(Electromechanics)[M]. 武汉：华中科技大学出版社(Wuhan: Huazhong University of Science and Technology Press)，2010.

[2] M Zaheeruddin, N Tudoroiu. Dual EKF estimator for fault detection and isolation in heating ventilation and air conditioning systems [A]. 38th Annual Conference on IEEE Industrial Electronics Society [C]. Montreal, Canada,2012. 2257-2262.

[3] 罗应立，赵海森, 姚丙雷，等(Luo Yingli，Zhao Haisen，Yao Binglei, et al.). 交流电机铁耗的工程计算方法分析 (AC motor iron loss analysis of the engineering calculation method) [J]. 电机与控制应用 (Electric Machines & Control Application)，2010, 37(11): 1-10.

[4] 张涵，谢宝昌，张舟云, 等 (Zhang Han, Xie Baochang，Zhang Zhouyun, et al.). 车用永磁同步电机铁耗的快速计算方法 (Fast calculation method of permanent magnet synchronous motor iron loss) [J]. 电机与控制应用 (Electric Machines & Control Application)，2013, 40(12): 9-14.

[5] 李子昀 (Li Ziyun). 一种考虑铁耗的感应电机最大效率控制系统 (A kind of induction motor considering iron consumption in the maximum efficiency control system) [J]. 大电机技术(Large Electric Machine and Hydraulic Turbine)，2011, (3): 17-27.

[6] Liu Xiaohu. Efficiency optimization control of induction motor drives [A]. International Conference on Electric Information and Control Engineering [C]. Wuhan, China, 2011. 2: 8-13.

[7] 裴文卉, 张承慧, 崔纳新，等 (Pei Wenhui, Zhang Chenghui, Cui Naxin,et al.). 电动汽车用感应电机最小损耗Hamilton控制 (The electric car with Hamilton minimum loss control of induction motor) [J]. 电机与控制学报 (Electric Machines & Control)，2012, 16(4): 1-7.

[8] M Hrke, J Vittek, Z Biel. Maximum torque per ampere control strategy of induction motor with iron losses [A]. IEEE Conference on Power Electronics [C]. 2012. 185-190.

[9] 丁树业, 刘书齐, 毕刘新，等 (Ding Shuye, Liu Shuqi, Bi Liuxin,et al.). 矢量控制下永磁同步电机的损耗分析(Vector control of permanent magnet synchronous motor loss analysis) [J]. 西安交通大学学报 (Journal of Xi’an Jiaotong University)，2013，47(12)：96-100.

[10] 李洁，杜茜，宋海军，等(Li Jie, Du Xi, Song Haijun, et al.). 考虑铁损的异步电机参数辨识实验研究 (Experimental evaluation of induction machine parameter identification considering iron loss) [J]. 电工技术学报 (Transactions of China Electrotechnical Society)，2014，29(3): 89-95.

(，cont.onp.80)(，cont.fromp.18)

Series-parallel motor model considering iron loss and its impact on vector control

LI Yao-heng1, DIAO Li-jun2

(1. School of Electrical Engineering, Beijing Jiaotong University, Beijing 100044, China；2. The Rail Transit Electrical Engineering Technology Research Center of Beijing, Beijing 100044, China)

Based on the analysis of the induction motor iron loss resistance, static α-βaxisisderivedundertheconsiderationofironlossandparallelequivalentcircuitofasynchronousmotor,andthestaticmodeloftheinductionmotorconsideringironlossisestablished.Underthestaticmodel,themodeloftheinfluenceofironlossofmotorvectorcontrolisanalyzed.Meanwhile,theequivalentcircuitofrotatingcoordinatesystemofinductionmotorinparallelconsideringironlossisestablished.Moreover,theequivalentcircuitissimplifiedinsteadystate.Inrotatingcoordinateanalysis,theinfluenceofironlossonvectorcontrolisconsidered.Furthermore,throughtheMatlab/Simulink,theproposedanalysisisverifiedbysimulationresults.Tofurtherimprovethecontrolprecisionandverifythetheoreticalanalysis,anexperimentiscarriedoutbasedontheHybridPowerCRHTrainGroundTestPlatformandthecontrolcenterofTMS320F28335.Thisresearchwillimprovethecontrolprecisionandprovidesreliablebasisforfurtherstudyofasynchronousmotoroptimalfluxcontrol.

induction motor; iron loss; vector control; magnetic field orientation

2015-04-20

“十二五”国家科技支撑计划项目(2015BAG13B01； 2013BAG21QB00)、 中央在京高校重大成果转化项目(ZDZH20141000401)

李耀恒(1990-)， 男， 河北籍， 硕士研究生， 研究方向为电力电子与电力传动； 刁利军(1980-)， 男， 广东籍， 副教授， 博士， 研究方向为电力电子与电力传动。

TM346

A

1003-3076(2016)01-0013-06