橡皮筋发动机
2016-05-24闵逸萌高文莉周子恒王思慧
闵逸萌,高文莉,周子恒,杜 立,王思慧
(南京大学 a.匡亚明学院; b.物理学院,江苏 南京 210093)

橡皮筋发动机
闵逸萌a,高文莉b,周子恒b,杜立b,王思慧b
(南京大学 a.匡亚明学院; b.物理学院,江苏 南京 210093)
摘要:研究了通过扭转橡皮筋作为驱动力的“发动机”的能量存储与输出. 根据观察定义了橡皮筋形变的多阶缠绕,在此基础上建立模型模拟了橡皮筋解旋的能量输出过程. 定义了该发动机的各项参量,包括总的旋转时间、有效旋转时间、效率等,探究了能量的分布情况. 实验结果表明:橡皮筋发动机的大部分能量转化为螺旋桨的动能和空气动能.
关键词:橡皮筋发动机;多阶缠绕;应变能;有效旋转时间;效率;CUPT/IYPT
本文是2014年“CUPT/IYPT”题目“Rubber Motor”的解答,原题为:经过扭转的橡皮筋可以储存能量,例如可以用来驱动模型飞机. 请研究该能量来源的特性,以及能量输出随时间变化的规律.
橡皮筋动力飞机是常见的玩具和简易飞机模型. 本文以玩具橡皮筋飞机作为发动机模型,研究其扭转过程中能量的存储,以及通过释放螺旋桨如何将应变能转换成空气动能、螺旋桨动能及摩擦耗散. 通过预实验发现在扭转圈数较大时,橡皮筋会发生多阶缠绕,为此将建立了数学模型,导出了多阶缠绕下存储应变能的公式. 根据能量守恒原理,考虑螺旋桨能量释放过程中各项功率与应变能的瞬时关系,得到了释放过程中螺旋桨转速随时间变化的微分方程,从而与实验结果做了对比.
1预实验
为了记录螺旋桨释放过程中转速的变化,采用如图1(a)所示的装置,先将模型飞机的“发动机”部分固定,将螺旋桨旋转一定圈数后释放,用高速相机(240帧/s)记录整个释放过程.
当初始转动螺旋桨时,橡皮筋会卷曲并均匀缠绕,缠绕到一定圈数时,橡皮筋已经缠满了1层. 此时如果继续转动螺旋桨,缠绕过一遍的皮筋将再次卷曲盘绕,称之为二阶缠绕;随着转动圈数的增加,还将出现三阶缠绕,等等,如图2所示. 在重复做了几次实验后,得到多阶缠绕的数据如表1中所示. 实验所用的橡皮筋参量为:截面2 mm×2 mm,长度30 cm,由2根并联而成.

(a)

(b)图1 实验装置

(a)一阶缠绕

(b)二阶缠绕

(c)三阶缠绕图2 3种缠绕情况

实验次数N一阶二阶三阶10~4646~201201~24020~5050~193193~24030~4242~208208~240多次实验平均范围0~5045~200200~240
旋转不同圈数后释放螺旋桨,此时叶片开始转动,利用图1中的装置获得转速与时间的关系,得到的结果如图3所示. 通过预实验, 观察到以下现象:
1)随着缠绕圈数的增加,螺旋桨解旋的总时间增长.
2)随着缠绕圈数的增加,螺旋桨的最大转速也会增加.
3)螺旋桨具有在一段时间内保持角速度不变的状态.

图3 螺旋桨转速曲线
2能量储存与释放的理论模型
2.1应变能与机械功
在螺旋桨被释放前,输入的机械功首先会以应变能的形式储存在扭曲的橡皮筋中. 先给出这部分能量所对应的公式.
引入x,y和z方向的拉伸比λ1,λ2和λ3. 对于不可压缩材料的单轴拉伸,有:λ1=λ和λ2=λ3=λ-0.5. 利用Mooney Rivlin模型[1], 橡皮筋的应变能可以表示为

(1)
其中参量C1和C2是与材料有关的常量. 假定输入的机械功全部转变为橡皮筋的应变能,通过测量伸长量(拉伸比)与拉力做的功的关系[2],由式(1)可拟合得到本实验中C1=0.190 J,C2=0.081 J.
为了建立转动的圈数与拉伸比λ之间的关系,建立如下模型. 假设模型发动机两端(固定橡皮筋用)的距离是l0, 当螺旋桨转动θ角度时,橡皮筋的长度从l0拉伸到lθ. 假设扭曲的橡皮筋可以看成是等距螺旋线,如图4(a)所示,最终长度lθ与初始长度l0的关系如图4(b)所示. 其中Rg是引入的有效缠绕半径. 因此,橡皮筋的拉伸比可以表示为

(2)
则三阶缠绕的拉伸比λ可分别为
(3)
其中λi是每一阶缠绕前的初始拉伸比,例如第一阶缠绕,λi是橡皮筋被固定到模型飞机上的初始拉伸比. 由于仅考虑三阶缠绕,根据实验数据,取N1=50,N2=200.

(a) (b)图4 等距螺旋线模型及最终长度lθ和 初始长度l0间的关系
显然在三阶缠绕的情况下,Rg不同.Rg的值可以从实验中获得.
在橡皮筋发动机的能量存储阶段,输入的机械功可以由橡皮筋的扭矩与旋转角度(圈数)的关系推算. 通过实验,测量得到扭矩与旋转圈数的关系,扭矩Mf=fd, 其中d是螺旋桨的半径,f为缓慢推动螺旋桨外端所使用的推力. 实验中每隔5圈测量1次螺旋桨上的扭力,其测量结果如图5所示. 图中曲线下方的面积S与机械功成正比,即W′=2πdS. 实际计算时假设每旋进5圈的扭力不变, 那么总的输入功可以表示为

图5 螺旋桨旋转的圈数N与受力f的关系
(4)
假设应变能与输入的机械功相等,即W=W′. 由实验测得的输入的机械功的值可以倒推拉伸比以及有效缠绕半径Rg的值.
2.2能量释放与分配
当螺旋桨解旋后,橡皮筋中储存的应变能将主要转换成螺旋桨的动能、空气动能及与螺旋桨轴之间的摩擦耗散. 根据能量守恒,可以得到:

(5)


(6)
Ip为螺旋桨的转动惯量.
Pair是螺旋桨推动空气的功率,其形式为[3]

(7)
其中,ρ为来流的气体密度,A是桨盘的面积,V0是未受螺旋桨扰动的轴向速度,对于通常的螺旋桨,a为8%~15%,取a=10%. 实验所用螺旋桨桨叶长度为8.70 cm.
本实验中,假设风速和螺旋桨的转速存在线性关系,即

(8)
则式(7)可变为
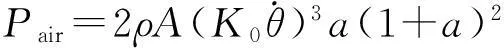
(9)
这代表了推动空气运动对应的功率. 至此,给出了式(5)中每一项与转速或者角位移的关系. 由实验确定各项系数后,就可以通过求解微分方程得到解旋过程中角速度与时间的关系,并由此计算在此过程中能量的分配情况.
3实验结果
3.1风速与螺旋桨转速的关系
利用如图1(b)的装置,测量了风速与螺旋桨转速的值,见图6. 实验验证了风速和转速之间存在线性关系,得到了比例系数K0=0.042 m/rad.
3.2解旋过程
以三阶缠绕为例分析转速随时间的变化情况. 图7为螺旋桨旋转240圈后释放的转速随时间的变化曲线. 显然三阶解旋的时间相对最短,在此阶段中转速以加速为主;在二阶解旋过程中,转速先下降,后趋于平稳,在相当一段时间内保持不变;最后经过一阶解旋,转速最终下降到0. 如果定义在最大速度Vmax到Vmax/e之间的时间为有效输出时间,则有效输出时间约10 s.

图6 风速V0与转速的实验图线

图7 三阶缠绕下的转速随时间的变化曲线
3.3发动机输出性能
由于从实验上已经得到了转速的变化曲线,按照式(9),容易求出空气动能或相应功率随时间的变化曲线,如图8(a)所示. 实验中螺旋桨的转动惯量为Ip=8.56×10-5kg·m2,橡皮筋推动螺旋桨的机械功率见图8(b),由图可知,在最初很短时间内(1 s左右)转速达到极大值,橡皮筋对螺旋桨做正功,Pp>0. 此后螺旋桨减速,对外释放能量,Pp<0.
推动空气运动的这部分功率被视为有用功率,空气运动的动能与输入功相比,可以得到发动机的效率. 空气运动的动能可以由图8的阴影面积求得. 而总的输入功可以从图5中得到,即W′=∑10πdfi.
由旋桨旋转240圈后释放的数据,可得到总的空气动能占输入能量的56.6%. 多次实验,在一阶、二阶和三阶缠绕条件下得到的结果如表2所示,表中Pmax为最大有用功率,t总为总持续时间,t有为有效时间.

(a)

(b)图8 推动空气的功率以及推动螺旋桨的 机械功率随时间的变化

N/圈Pmax/Wt总/st有效/sη200.00437.26.081.5%1100.1412.29.461.6%2400.7615.010.656.6%

4理论与实验对比
根据实验条件确定式(5)中的各项系数后,就可以通过求解微分方程,得到解旋过程角速度与时间的关系. 通过计算得到螺旋桨在旋转20,110,240圈后释放的角速度与时间关系,见图9.

(a)20圈

(b)110圈

(c)240圈图9 角速度与时间关系
经对比发现,理论结果与实验值基本吻合,但在实验中没有明显地出现转速稳定的平台阶段 (尤其在一级缠绕中存在转速稳定的平台,提示模
型过于简化,可能由于忽略了拉伸和释放过程的非线性和摩擦导致的).

图10 发动机能量随时间的变化(240圈)
5结束语
研究了橡皮筋发动机性质,结合多阶缠绕的实验现象,给出了储存应变能的公式. 经过实验测量和理论分析,给出了螺旋桨转速与时间的变化关系,空气动能、螺旋桨动能以及总能量的变化情况. 定义了该发动机的各项参量,包括总的旋转时间、有效旋转时间、效率等. 理论模型与实验结果对比符合较好.
致谢:感谢杨王飞同学无私的帮助和鼓励.
参考文献:
[1]James H M, Guth E. Theory of the elastic properties of rubber [J]. Journal of Chemical Physics, 1943,11(10):455-481.
[2]左亮,肖绯雄. 橡胶Mooney-Rivlin模型材料系数的一种确定方法[J]. 机械制造,2008,46(7):38-40.
[3]刘沛清. 空气螺旋桨理论及其应用[M]. 北京:北京航空航天大学出版社,2006:56-62.
[责任编辑:任德香]
Rubber band motor
MIN Yi-menga, GAO Wen-lib, ZHOU Zi-hengb, DU Lib, WANG Si-huib
(a. Kuang Yaming Honors School; b. Physics School, Nanjing University, Nanjing 210093, China)
Abstract:The properties of a rubber band motor, a toy motor that stores mechanical energy in a twisted rubber band and releases the energy through an aircraft propeller in an unwinding process, was systematically studied. The strain energy stored in the winded band was converted into three parts: kinetic energy of air, kinetic energy of propeller, frictional dissipation of propeller. For each one of them, a mathematical model was built to account for its contribution to the motor performance. Particularly, configurations of a twisted rubber band were classified into three types: the primary winding, the secondary winding and the tertiary winding. Various properties revealed by the experiment were clarified by our theory.
Key words:rubber motor; kink configurations; strain energy; effective spinning time; efficiency; CUPT/IYPT
中图分类号:O344.1
文献标识码:A
文章编号:1005-4642(2016)04-0027-05
作者简介:闵逸萌(1995-),男,江苏苏州人,南京大学匡亚明学院2013级本科生.指导教师:王思慧(1964-),女,北京人,南京大物理学院教授,博士,从事基础物理理论与实验教学.
收稿日期:2015-12-31
