考虑刚-柔-热耦合的板结构多体系统的动力学建模*
2016-05-24张炜华刘锦阳
张炜华 刘锦阳
(上海交通大学工程力学系,上海 200240)
考虑刚-柔-热耦合的板结构多体系统的动力学建模*
张炜华 刘锦阳†
(上海交通大学工程力学系,上海 200240)
对热载荷作用下中心刚体与大变形薄板多体系统的动力学建模问题进行研究.基于Kirchhoff假设,从格林应变和曲率与绝对位移的非线性关系式出发,推导了非线性广义弹性力阵,用绝对节点坐标法建立了大变形矩形薄板的有限元离散的动力学变分方程.为了考虑刚体姿态运动、弹性变形和温度变化的相互耦合作用,推导了热流密度与绝对节点坐标之间的关系式.引入系统的运动学约束方程,建立了中心刚体-矩形板多体系统的考虑刚-柔-热耦合的热传导方程和带拉格朗日乘子的第一类拉格朗日动力学方程.为了有效地提高计算效率,将改进的中心差分法和广义-α法相结合,求解热传导方程和动力学方程,差分后的方程通过牛顿迭代法耦合求解.对刚-柔耦合和刚-柔-热三者耦合两种模型的仿真结果进行比较表明,刚体运动对温度梯度和热变形的影响显著.此外,本文建模方法考虑了几何非线性项,因此也考虑了热膨胀引起的轴向变形对横向变形的影响.
大变形薄板多体系统, 刚-柔-热耦合, 改进的中心差分法
引言
航天器太阳帆板或者太阳帆板的组成构件多为板式结构.在轨航天器沿轨道飞行或者航天器的太阳帆板展开过程中,太阳帆板会受到周期性、不均匀的太阳光照射,太阳帆板上下表面的热流密度的差异引起太阳帆板沿厚度方向温度梯度,导致沿厚度方向的热膨胀不均匀,从而诱发太阳帆板的热振动,在一定程度上会影响航天器的姿态运动.
Thornton和Kim[1]在不考虑航天器运动的情况下建立了卷筒式太阳电池阵热与结构耦合的动力学模型,研究了热与结构耦合的动力学特性,然后Johnston和Thornton[2]在考虑航天器的姿态运动的情况下,研究了在轨运动航天器在太阳辐射热流作用下太阳帆板的热诱发振动对航天器姿态运动的影响.在此基础上,Johnston和Thornton[3]进一步开展了动力学实验,验证了理论结果的准确性.笔者[4]将热与结构耦合的动力学模型推广到薄板结构,研究了刚-柔-热耦合特性.以上研究工作均基于线弹性理论,仅适用于小变形问题.
由于温度上升幅值较大,需要考虑太阳帆板热膨胀引起的轴向变形对弯曲变形的影响.此外,由于太阳帆板具有质量轻和尺度大的特点,弹性变形较为显著,因此,为了保证计算结果的准确性,在建立动力学方程的过程中需要考虑几何非线性项.在几何非线性动力学研究方面,国内外学者针对大变形板壳构件的力学研究开展了一系列工作.Oguamanam等学者[5]针对热冲击作用下中心刚体和复合材料层合壳组成的多体系统,利用Von Karman应变与位移的关系建立了考虑几何非线性的刚-柔耦合动力学方程,在研究刚-柔耦合特性的同时,研究了几何非线性项对动力学特性的影响.笔者[6]从Green应变与位移的关系式出发,建立了热载荷作用下作任意大范围运动柔性梁的几何非线性动力学方程,对温度升高引起的动力软化问题进行了分析.以上研究工作均假定温度场是给定的,无法对刚-柔-热耦合机理进行分析.此外,在推导弯曲应变的过程中利用了板壳曲率的近似表达式,对于大变形问题,容易导致数值计算误差.
目前,Shabana提出的绝对节点坐标法已广泛应用于大变形柔性多体系统动力学分析,该方法的特点是选取柔性梁或柔性板各单元节点相对惯性基的位移和斜率作为广义坐标,建立动力学方程[7-8],这样就不需要引入大范围运动变量和变量位移坐标,广义坐标全部是全局坐标,得到的质量阵为常值阵,广义力的表达式也比较简单.Dombrowski等学者[9]用绝对节点坐标法对大变形薄板的动力学建模理论进行研究,建立了矩形薄板的二维有限元模型.Mikkola[10]等学者进一步考虑剪切变形,建立了三维矩形薄板的有限元模型.为了验证绝对节点坐标法的正确性,Yoo等学者[11-12]首先用快速相机对大变形薄板进行实验研究,并将测量技术推广到大变形复杂结构多体系统.赵将等学者[13]针对简化的“IKAROS”自旋展开太阳帆系统,采用结合自然坐标方法与绝对节点坐标方法的绝对坐标方法对其进行建模,研究了黏弹性太阳帆薄膜自旋展开过程的动力学特性.
为了保证刚-柔耦合动力学仿真精度,本文采用绝对节点坐标法对热载荷作用下中心刚体-薄板多体系统进行动力学建模.不计薄板的面外剪切变形,基于Kirchhoff假设,从格林应变和曲率与绝对位移的精确关系式出发,推导了非线性广义弹性力阵,用绝对节点坐标法建立了大变形复合材料薄板的有限元离散的动力学变分方程.在此基础上进一步考虑刚体姿态运动、弹性变形和温度变化的相互耦合作用,建立了热流密度与绝对节点坐标之间的关系式,推导了中心刚体-矩形板的刚-柔-热三者耦合的热传导方程和动力学方程.考虑到Runge-kutta法的计算效率较低,本文用广义-α法求解动力学方程,用改进的中心差分法求解热传导方程,差分后的方程通过牛顿迭代法耦合求解.通过仿真算例对无耦合模型,刚-柔-热耦合的仿真结果进行分析,得到了对工程实际具有参考价值的结论.
1 热载荷作用下矩形薄板的动力学方程

大变形矩形薄板如图1所示,设板的长度为a,宽度为b,厚度为h,体密度为ρ.建立固结在地面的惯性坐标系有限元方法将矩形薄板等分为n=n1×n2个单元,对第e个单元建立单元坐标系则板单元的长度和宽度分别为ae=a/n1,be=b/n2.设(x,y,0)为薄板中面上任意一点在该单元坐标系下的坐标,基于绝对节点坐标法,中面上对应点k0的绝对位置矢量在惯性坐标系下的坐标阵为:


图1 大变形矩形薄板Fig.1 Thin rectangular plate with large deformation
其中,S(x,y)为形函数矩阵,由文献[11]给出.qe(t)为单元节点的绝对位置坐标,位置坐标分别对x,y的一阶导数,以及位置坐标对x和y的两阶导数在惯性基下的坐标阵,qe(t)表达式分别为:

其中,qke(t),k=1,…,4为单元4个节点的绝对节点坐标列阵,具体表述方式如下:

设q(t)为总体绝对节点坐标列阵,qe(t)与q(t)的关系为qe(t)=Beq(t),其中,Be为单元e的布尔阵.
基于Kirchhoff假设,不计板的剪切变形,为了表示任意一点k的应变,引入点k所在中面上相对应点k0的应变列阵ε0,设n0(x,y,t)为变形后沿法线的单位矢量,基于Kirchhoff假设,法线n0(x,y,t)与中面保持垂直.格林应变的表达式可写成:

其中,ε0为中面的面内应变列阵,可表示为:

κ为中面的曲率列阵,可表示为:

1.1 质量阵和广义外力阵的推导
针对薄板问题,可以忽略绝对位移沿单元坐标系Ze方向的变化,板单元e的惯性力的虚功率为:

将式(2)代入上式:

其中,单元质量阵Me为:
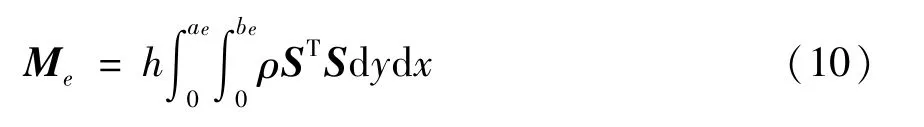
矩形薄板的惯性力的虚功率为:


利用关系式(2),板单元体力的虚功率为:
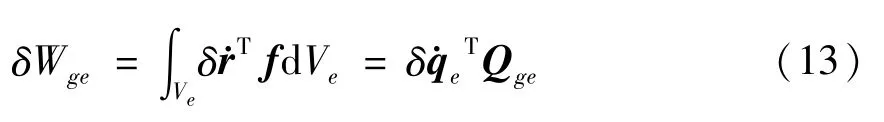
其中,单元体力列阵Qge为:

体积力的虚功率为:
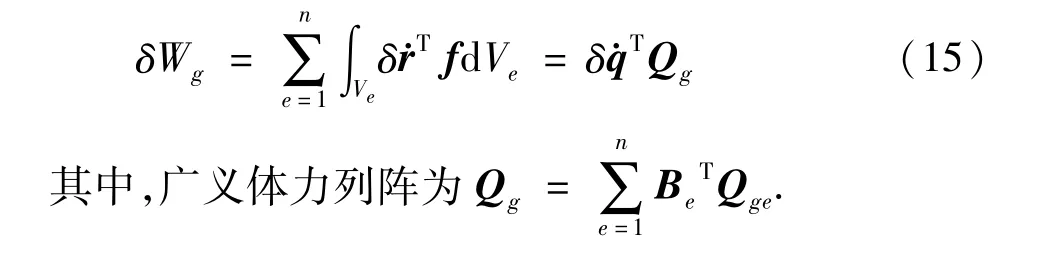
1.2 广义弹性力阵的推导
对中面的面内应变求变分,并利用关系式(2),得到:

其中,

基于Kirchhoff假设,中面的单位法向量在惯性基下的坐标阵n0可表示为:

其中,n为rx与ry的叉积,n为矢量n的模,可表示为:

对(19)求变分,利用式(2),得到:

将式(18)代入(7),得到κ的表达式为:

对式(24)求变分,并利用关系式(2),得到:

下面推导薄板在热载荷作用下,当温度变化ΔT时,板结构的热应变可表示为[6]:

薄板结构的应力与应变的本构关系可表示为:

其中,E为弹性模量,γ为泊松比.
板单元弹性力的虚功率为:

将式(5)和(28)代入式(31)可得板弹性力的虚功率的表达式为:

化简后得到板的弹性力虚功表达式:

其中,单元广义弹性力阵的具体表达式为:

根据虚功原理,动力学变分方程为:

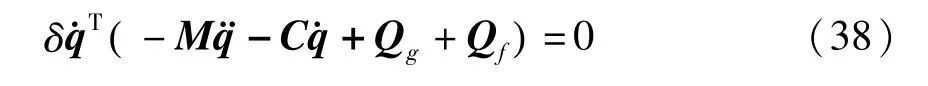
1.3 中心刚体和薄板多体系统的动力学方程
设中心刚体的质量为mr,关于过质心主轴的转动惯量阵为J′,以中心刚体质心C为原点建立连体基质心C相对惯性基的位置矢量在惯性基下的坐标阵为rC,连体基相对惯性基的角速度矢量在连体基下的坐标阵为ω′C,中心刚体的动力学变分方程为:

其中,FC为作用于中心刚体的外力的主矢在惯性基下的坐标阵,M′C为作用于中心刚体的外力关于质心的主矩在连体基下的坐标阵.

中心刚体的动力学变分方程为:

中心刚体和矩形薄板多体系统的动力学变分方程为:

设柔性多体系统的约束方程为:

柔性多体系统含拉格朗日乘子的第一类拉格朗日动力学方程为:

其中,

Φq为约束方程的雅可比矩阵,λ为由拉格朗日乘子构成的列阵.
将式(45)和(46)联立构成微分代数混合方程:

2 热传导方程
2.1 热传导方程
在三维情况下,温度场变量T在笛卡尔坐标系中满足的热传导变分方程为:

其中,c是材料的比热容,k是材料的热传导系数,Q是物体内部的热源密度,q+、q-分别为上下表面的热流密度分别为上下表面的外界环境温度,hc为换热系数.其余边界处绝热,仅有上下表面是传热的.
设TN与TM分别是板中面上任意一点的温度变化和沿厚度方向的温度梯度,T0为参考温度,则对于比热容不大的情况,非中面上任意一点的温度可表示成T=T0+TN+zTM,即非中面上任意一点的温度变化为ΔT=TN+zTM.将公式(51)和(52)代入热传导变分方程(50),得到:


将式(54)代入变分方程(53),则有限元离散柔性板的热传导变分方程为


2.2 考虑刚-柔-热耦合的热流密度q的推导
假设上下表面的换热系数为0,板内部的热源密度为0,本文考虑的热流密度q主要来源于宇宙中太阳辐射的热流.图2所示为太阳帆板上任意点的中面法线矢量和太阳光辐射矢量.

图2 有大范围运动的太阳帆板Fig.2 The solar plate with large overallmotion

其中,n为矢量n的模,由式(20)给出.将式(66)代入式(67),太阳直接辐射角系数可以表示为:

上式表明,太阳直接辐射系数为矩阵的绝对节点坐标q的函数,说明太阳直接辐射角系数与太阳帆板的刚体运动和弹性变形三者相互耦合.
为了区分究竟是单元的上表面还是下表面对着太阳,太阳直接辐射角系数Γα可以修改为:

求得太阳直接辐射角系数Γ后,考虑刚-柔-热耦合的热流密度可表示为:

将式(52)和(54)代入(35),单元广义弹性力阵Qfe3和Qfe4的具体表达式为

根据热流密度的表达式(68)可知,本文建立的热流密度函数与薄板的绝对节点坐标有关系,而薄板的绝对节点坐标q和刚体运动以及柔性体的弹性变形相关,那么基于公式(48)和(63)建立的动力学模型即为本文提出刚-柔-热三者耦合模型.若在建模中忽略中心刚体的姿态运动和薄板的弹性变形对热流密度影响,则任意点的法线矢量阵n为常值,此时计算得到热流密度与薄板的绝对节点坐标q并无关系,仅与太阳常数S有关,那么基于此种工况的热流密度建立的动力学模型就是无耦合的动力学模型.由此可见,刚-柔-热三者耦合的动力学模型是最精确的力学模型.
3 数值计算方法
3.1 刚-柔-热耦合多体系统的动力学方程
将热传导方程和刚体与板的动力学方程联合,结合公式(48)和(65)建立刚-柔-热耦合多体系统动力学方程如下:

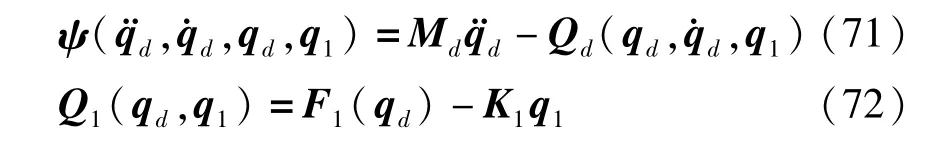
3.2 数值计算方法
为了在保证计算精度的同时保证刚-柔-热耦合动力学方程的计算效率,本文采用对动力学方程用广义-α法构造差分格式,而热传导方程用改进的中心差分法构造差分格式,两者联立后用Newton-Raphson方法求解微分代数混合方程(71).计算步骤为:
(1)动力学方程运用广义-α法构造的差分格式如下:

对热传导方程采用改进的中心差分格式后可变为:

(2)将差分格式(76)~(78)代入方程(73)后使用牛顿-拉斐逊迭代法求解联合方程组如下:



4 数值仿真
本算例中,用中心刚体模拟卫星的舱体,薄板结构模拟太阳帆板.中心刚体关于质心连体基的转动惯量为Jx=Jy=Jz=200kg·m2,太阳帆板长为7.5m,宽为0.5m,厚度为0.0103m,采用航空航天工程中常用的低密度、低导热系数的各向同性材料,其弹性模量E=1.93×109N/m2,密度36.8kg/m3,导热系数k=1.5W/(m·K),比热容c=921J/(kg ·K),热膨胀系数α=2.3×10-5K-1,帆板的表面吸收率αm=0.79,太阳常数S=1350W/m2.太阳帆板与中心刚体通过固支铰连接.设结构阻尼系数为c=0.01.
设太阳入射角为α0,即与惯性基的夹角为π-α0,则在惯性基下的坐标阵为s=下面对卫星太阳帆板姿态机动的整个驱动过程进行模拟,以研究太阳热辐射对整个动力学过程的影响.设中心刚体质心C相对惯性基静止,绕轴作定轴转动.初始时刻,中心刚体连体基相对惯性基的三个姿态角均为0,参考温度为0.本算例在中心刚体上施加方向驱动力偶,其时变历程如图3所示.太阳辐射的入射角为α0=65°.

图3 驱动力偶Fig.3 Driving torque

图4 中心刚体C方向转角Fig.4 Rotational angle of the hub alongCaxis
图4和图5分别为计算得到的中心刚体转角和角速度的时变图,第一阶段中心刚体绕轴加速转动,当时间t大于25s时,由于驱动力偶为0,停止加速,角速度在平均值附近振动,第二阶段角速度的平均值为常数.当时间t大于175s时,开始第三阶段的减速.当时间t大于200s,驱动力偶为0,角速度在0附近振动,停在固定角度,也就是第四阶段.从图中可以看出,非耦合模型和刚-柔-热耦合模型的得到的中心刚体方向转角基本吻合.

图5 中心刚体C方向角速度Fig.5 Angular velocity of the hub alongCaxis
图6为帆板中面上角点P的沿厚度温度梯度曲线.图7为帆板中面上角点P沿方向纵向变形.图8为沿方向横向变形.从图中可以看到,对于刚-柔-热三者耦合模型,由于热流密度的表达式中考虑了角系数与薄板绝对位移坐标的关系,当航天器受到驱动力偶作用作定轴转动时,沿厚度方向的温度梯度呈现周期性变化,当姿态机动到位时,沿厚度方向的温度梯度保持不变.而无耦合模型由于热流密度为常数,沿厚度方向的温度梯度始终保持不变.此外,对于无耦合模型,由于沿厚度方向温度梯度为常数,P点横向变形和沿方向纵向变形均不受刚体转动的影响.对于刚-柔-热三者耦合模型,P点横向变形为高频和低频振荡曲线的迭加,而低频振荡的频率正是沿厚度方向温度梯度振动的频率.除了横向变形,沿方向纵向变形在缓慢增大的同时(热膨胀引起),也呈现周期性的波动.可以看出,当姿态机动到位时,本文非线性模型得到的横向变形平均值的绝对值明显大于不考虑纵向变形影响的传统的线性模型.
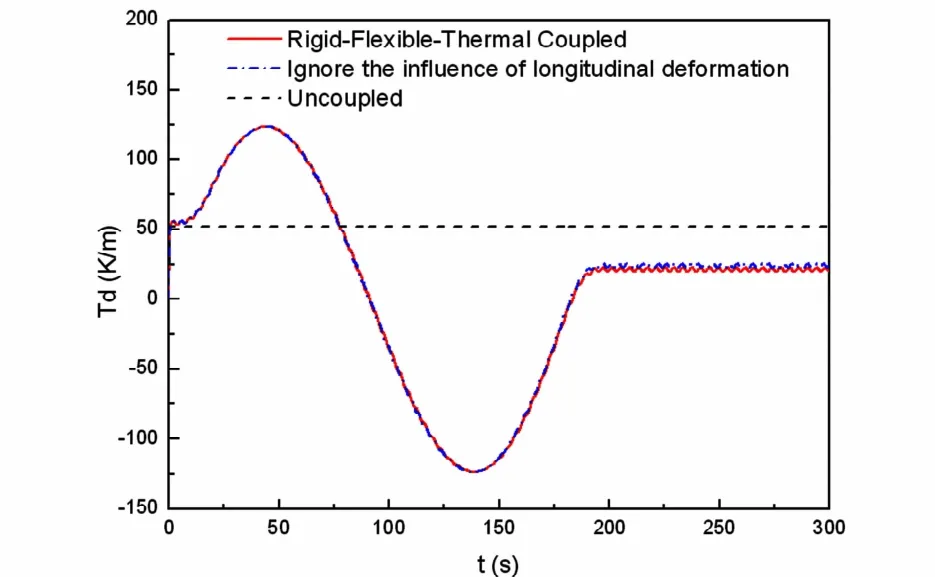
图6 P点厚度方向温度梯度Fig.6 Temperature gradient of PointPin thickness direction
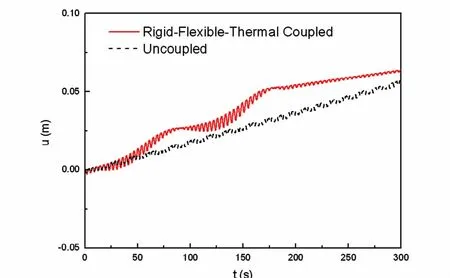
图7 P点沿C方向纵向变形Fig.7 Longitudinal deformation of PointPalongCaxis
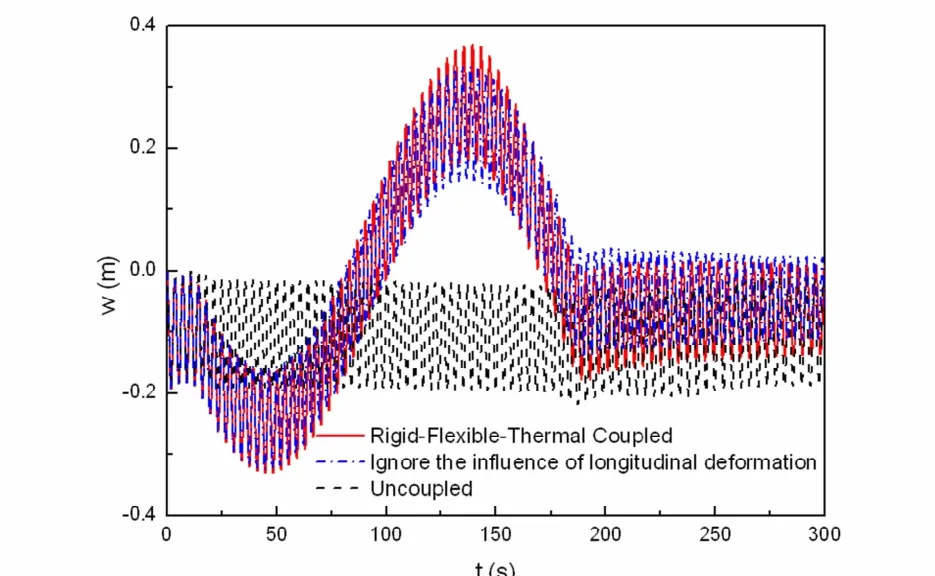
图8 P点沿C方向横向变形Fig.8 Transverse deformation of PointPalongCaxis
5 结论
基于热传导方程和有限元离散化方法,建立了热传导方程的变分方程,考虑刚体姿态运动、弹性变形和温度变化的相互耦合,建立了热流密度与刚体姿态坐标和弹性坐标的精确关系式.结合刚-柔耦合动力学方程和热传导方程.考虑热边界条件随刚体运动和弹性变形的变化,建立了具有通用形式的刚-柔-热耦合多体系统的动力学方程.为了有效地提高计算效率,将改进的中心差分法和广义-α法相结合,求解热传导方程和动力学方程,差分后的方程通过牛顿迭代法进行求解.
对无耦合模型和刚-柔-热三者耦合模型的仿真结果进行比较表明,中心刚体的姿态运动对沿厚度方向温度梯度和热变形的影响不容忽视,表现在沿厚度方向温度梯度呈现周期性的振荡.此外,横向变形和纵向变形曲线是低频振动和高频振动曲线的迭加,低频振动频率等于沿厚度方向温度梯度振动的频率.进一步研究还发现,本文非线性模型得到的横向变形平均值的绝对值明显大于不考虑轴向变形对横向变形影响的传统的线性模型.从而说明当轴向变形随着温度升高逐渐增大时,轴向变形在方向的分量对横向变形具有一定影响,不容忽视.
1 Thornton E A,Kim Y A.Thermally induced bending vibrations of a flexible rolled-up solar array.Journal of Spacecraft and Rockets,1993,30(4):438~448
2 Johnston J D,Thornton E A.Thermally induced attitude dynamics ofa spacecraftwith a flexible appendage.Journal of Guidance,Control and Dynamics,1998,21(4):581~587
3 Johnston JD,Thornton E A.Thermally induced dynamics of satellite solar panels.Journal of Spacecraft and Rockets,2000,37(5):604~613
4 潘科琪.曲梁和板壳结构多体系统刚-柔耦合动力学研究[博士学位论文].上海:上海交通大学,2012(Pan K Q.Rigid-flexible coupling dynamics for curved beam and shell structuremultibody systems.[PhD Thesis]Shanghai:Shanghai Jiao Tong University,2012(in Chinese))
5 Oguamanam D CD,Hansen JS,Heppler G R.Nonlinear transient response of thermally loaded laminated panels.ASME Journal of Applied Mechanics,2004,71(1):49~56
6 Liu JY,Lu H.Thermal effecton the deformation of a flexible beam with large kinematical driven overall motions.European Journal of Mechanics A/Solids,2007,26(1):137~151
7 Berzeri M,Shabana A A.Development of simple models for the elastic forces in absolute nodal co-ordinate formulation.Journal of Sound and Vibration,2000,235(4):539~565
8 Berzeri M,Shabana A A.Study of the centrifugal stiffening effect using the finite element absolute nodal coordinate formulation.Multibody System Dynamics,2002,7(4):357~387
9 Dombrowski SV.Analysis of large flexible body deformation in multibody systems using absolute coordinates.Multibody System Dynamics,2002,8(4):409~432
10 Mikkola A M,Shabana A A.A non-incremental finite element procedure for the analysis of large deformation of plates and shells inmechanical system applications.Multibody System Dynamics,2003,9(3):283~309
11 Yoo W S,Kim M S,Mun SH,Sohn JH.Large displacement of beam with basemotion:flexiblemultibody simulations and experiments.Computing Methods Applied Mechanical Engineering,2006,195(50):7036~7051
12 YooW S,Kim M S,Mun SH,Sohn JH.Developments of multibody system dynamics:computer simulations and experiments.Multibody System Dynamics,2007,18(1):35~5
13 赵将,刘铖,田强,胡海岩.黏弹性薄膜太阳帆自旋展开动力学分析.力学学报,2013,45(2):746~754(Zhao J,Liu C,Tian Q,Hu H Y.Dynamic analysis of spinning deployment of a solar sail composed of viscoelastic membranes.Chinese Journal of Theoretical and Applied Mechanics,2013,45(2):746~754(in Chinese) )
RIGID-FLEXIBLE-THERMALCOUPLING DYNAM IC FORMULATION FOR HUB-PLATE MULTIBODY SYSTEM*
Zhang Weihua Liu Jinyang†
(Department of Engineering Mechanics,Shanghai Jiaotong,University,Shanghai200240,China)
In this paper,rigid-flexible-thermal coupling dynamic formulation for hub rectangular platemultibody system with large deformation under thermal load is investigated.Based on Kirchhoff assumption,and the nonlinear relationships among the Green strain,the curvature and the absolute coordinates,the nonlinear elastic force is derived.Additionally,the finite element discretized dynamic variational equations of the rectangular plate are derived using absolute nodal coordinate formulation.In order to investigate the rigid-flexible-thermal coupling effect,the relationship between the heat flux and the absolute coordinates is also obtained.And through the constrained equations of themultibody system,the rigid-flexible-thermal coupling equations are derived,which include the heat conduction equations and the Lagrange dynamic equations of the first kind.Moreover,in order to improve the simulation efficiency,modified central differencemethod and generalized-a method are combined to solve the heat conduction equations and the dynamic equations.And the discretized equations are solved by using Newton-Raphsonmethod.Satellite and platemultibody system applied with solar heat flux is taken as examples to verify the effectiveness of the formulation.Comparison of the results obtained by non-couplingmethod and rigidflexible-thermal couplingmethod shows that the effect of the rigid bodymotion on the temperature gradient in the thickness direction and thermally induced deformation is significant,which should be taken into account.Furthermore,due to the inclusion of the geometric nonlinear terms,the influence of the axial deformation caused by the temperature increase on the transverse deformation is also taken into consideration.
hub-platemultibody system, rigid-flexible-thermal coupling, modified central differencemethod
10.6052/1672-6553-2015-88
2015-4-8收到第1稿,2015-11-12收到修改稿.
*国家自然科学基金资助项目(11272203,11132007)
†通讯作者E-mail:liujy@sjtu.edu.cn
Received 8 April2015,revised 12 November 2015.
*The project supported by the National Natural Science Foundation of China(11272203,11132007)
†Corresponding author E-mail:liujy@sjtu.edu.cn
