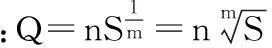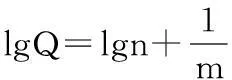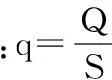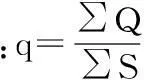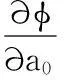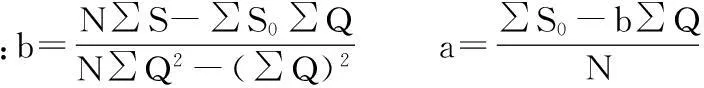浅谈煤矿防治水规定中单位涌水量的换算分析与应用

王　灿，孟怀安

(安徽省煤田地质局水文勘探队，安徽 宿州 234000)



浅谈煤矿防治水规定中单位涌水量的换算分析与应用

王灿，孟怀安

(安徽省煤田地质局水文勘探队，安徽 宿州 234000)

[摘要]依据煤矿防治水规定、煤矿床水文地质、工程地质及环境地质勘查评价标准、水文地质手册、对抽水实验钻孔单位涌水量曲线来确定最佳选配类型，换算成口径91 mm，抽水水位降深10 m来评价其富水性。

[关键词]煤矿防治水规定；抽水试验；涌水量公式；口径91 mm；降深10 m

根据《煤矿防治水规定》(国家安全监管总局令第28号)已于2009年12月1日起施行，各大煤矿企业深入贯彻《防治水规定》，加强煤矿防治水工作，对井田内主要充水含水层进行水文地质补勘工作，建立水位动态长期监测网，有效防范遏制煤矿重特大水害事故，为促进煤矿安全生产，将含水层富水性按钻孔单位涌水量(q)以口径91 mm、抽水水位降深10 m为准分为以下4级：

(1)弱富水性：q≤0.1 L/s·m；

(2)中等富水性：0.1 L/s·m

(3)强富水性：1.0 L/s·m

(4)极强富水性：q>5.0 L/s·m。

若口径、降深与上述不符时，应当进行换算后再比较富水性。下面结合日常学习和工作实践及参考资料，就其换算的过程与其浅谈。共分三部分：一是根据抽水试验Q=f(s)曲线确定涌水量的经验公式，二是换算成口径91 mm，降深10 m的单位涌水量，三是结合工程实例演示其过程。

1涌水量经验公式的选配

计算井涌水量的稳定流理论公式在导出过程中假定了许多理想的水文地质条件，而在实际抽水时往往超出了这些假定条件，计算时带来较大的误差。在生产实践中，常常根据抽水试验资料做出水井的流量Q与水位降深S之间关系曲线，然后由该曲线通过数学方法找出Q和S之间关系的表达式，即配出经验公式，然后用它进行水位或流量的预测。选配经验公式的一般步骤如下：

(1)根据抽水试验资料，得到每一抽水落程稳定时的流量Q和水位降深S，做出Q～S曲线。

(2)根据Q～S曲线的形状，判断经验方程的类型。

(3)确定经验公式的系数，建立经验公式。

(4)根据经验公式，进行流量(或降深)的预测。一般预测的降深不能超过抽水试验时最大降深的1.5～2倍。不允许利用降深很小的试验资料所建立的经验公式来预测大降深时的流量。

1.1Q=f(s)曲线类型

抽水试验出现不同类型的Q=f(s)曲线，是与试验地区地段的水文地质条件密切相关的，同时也与井位、井(孔)结构、试验方法等因素有关，只有当井(孔)位置、结构、试验方法等合理的前提下，曲线类型才能正确反映当地的水文地质条件。根据实践经验，当抽水时间相当长，在抽水井内及井附近地区地下水运动出现相对稳定状态时，承压水的涌水量(Q)与水位降深(S)的关系曲线有直线型、抛物线型、幂函数曲线型、对数曲线型等多种类型。当然，在实际抽水试验时也可能遇到其他类型的曲线，可用类似的方法处理。

1.1.1直线型

表示满足承压水的裘布依公式，Q和S有如下关系：

Q=qs

承压井出现Q=f(S)为直线的条件是：抽水试验条件接近于裘布依推导时的假定条件，即含水层比较均质，厚度变化小，近乎水平，渗透性强，补给条件好，水位降深较小，井孔附近阻力甚小，整个流程为二维流，渗流符合达西定律。

1.1.2抛物线型

涌水量曲线方程式为：S=aQ+bQ2

式中：a、b为待定系数，根据抽水试验资料确定，该方程称为凯列尔公式。

将公式两边除以Q，得到直线化抛物线涌水量曲线方程：即S/Q=a+bQ S/Q=S0，

得：S0=a+bQ

抛物线型曲线，一般代表含水层的补给条件较好，分布比较广、厚度比较大、透水性比较强，水量比较丰富的一种特征曲线。抽水井的出水量、水位都比较容易达到相对稳定。停抽后，水位恢复很快，水位恢复曲线拐折点明显，当出现拐折点很快能达到或者非常接近抽水前得稳定水位。

1.1.3幂函数曲线型

式中：n、m为待定系数，根据抽水试验资料确定，该方程又称为斯姆列盖尔公式。

对式等号两边取对数，既得直线化的指数曲线方程：

此类曲线常出现在含水层渗透性能较好，其厚度相对较大，补给来源相对较差的地区。反映在抽水试验过程中特点是：当水位降深较小时，出水量随着水位降深的加大增加的幅度较大。当水位降到一定深度后，出水量随着水位降深的加大而增加的幅度变得很小。抽水井的水位、水量不易达到相对稳定，它将随着时间的延续呈现明显的有系统的下降趋势。水位恢复曲线一般拐点仍明显，但拐折点之后经过较长时间才能接近抽水的得稳定水位。

1.1.4对数曲线型

其方程式为：Q=a+blgS

式中：a、b为待定系数，根据抽水试验资料确定，该方程又称为阿里托夫斯基公式。

对数型曲线常出现在一些相对隔离的含水层、含水体，其分布范围较大，地下水补给条件较差。抽水过程中，出水量随着水位降深的加大增加的很小，在Q=f(s)曲线图上，曲线靠近s轴，每次降深的水位、水量都很难达到稳定，随着抽水时间的延续呈现阶梯状的系统下降，整个抽水过程地下水呈现非稳定运动状态。停抽后，水位恢复很慢，拐点不明显，而且恢复不到抽水试验前的稳定水位。

1.2Q=f(s)曲线类型的鉴别方法

鉴别涌水量曲线类型的方法，目前常用的有伸直法(图解法)，差分法和曲度法。

1.2.1伸直法

根据三次以上不同水位降深的抽水试验资料绘制Q=f(s)曲线，若Q=f(s)是直线关系，则很容易判断涌水量曲线为直线型。若不是直线关系，则将曲线方程以直线关系式表示，并以直线关系式中两个相对应的函数建立坐标系。

即把抽水试验取得的涌水量和相对应的水位降深资料以S0、Q，lgQ和Q、lgS为直角坐标系分别绘制S0=f(Q)，lgQ～f(lgS)和Q～f(lgS)曲线，进行伸直判别，其中呈直线者，即为待确定的曲线类型。

1.2.2差分法

根据差分理论，凡属同一直线方程其一阶差分均相等，即为一常数，因此直线化后的各种曲线方程的一阶差分也应相等。这样，就可以利用差分原理，对各种类型曲线进行判别计算，其判别公式如下：

直线型Q=qS

抛物线型S0=a+bQ

对数型Q=a+blgS

若计算结果上述各方程中的一阶差分不相等，则曲线不完全适合所确定的方程类型，此时可根据差分误差计算进行判别比较。一阶差分误差的大小可用曲线拟合误差C表示：

1.2.3曲度法

用曲度n值进行鉴别，其表达式如下：

当n=1时，为直线型；当n=2时，为抛物线型，当12时，为对数型，如果n<1一般为异常型曲线(抽水资料有误)。

1.3确定涌水量曲线方程式中待定参数的方法

1.3.1作图选点法

将抽水试验实测数据，按直线关系点入相应的直角坐标图中，作一直线，使该直线通过实际资料点最多，同时使直线不能通过的点均匀地分布在直线的两侧。直线画出后，可以选取该直线上任意点或者根据直线两要素(斜率和截距)来计算参数。参数a为坐标系中截距，可直接量得，参数b是其直线段斜距(正切)，可分别变成：

1.3.2均衡误差法(分组平均法)

根据二次不同降深的抽水资料，作联立方程求得：

抛物线方程：

幂函数曲线程：

对数曲线方程：

1.3.3最小二乘法

(N为抽水试验的落程次数)

以上介绍的确定涌水量曲线方程中参数的方法，以作图选点法最为简单易作，但精度低，最小二乘法是几种方法中精度最高的，但它的计算工作量最大。

一般的方式，采用伸直法及曲度法判定涌水量曲线类型，采用最小二乘法确定待定系数。

2单位涌水量的换算

按规程要求，野外抽水试验孔径一般≥108 mm，依据《煤矿床水文地质、工程地质及环境地质勘查评价标准》，含水层富水性评价时，单位涌水量统一到以口径91 mm抽水水位降深10 m为准，因而要进行井径换算，其方法：

根据Q-S曲线类型确定降深10 m时抽水孔的涌水量，再用下面公式计算口径为91 mm时的涌水量，最后除以10 m，便是单位涌水量。

(1)

式中：Q91、R91、r91为孔径为91 mm的钻孔的涌水量、影响半径和钻孔半径；Q孔、R孔、r孔为孔径为r的钻孔的涌水量、影响半径和钻孔半径

(1)式为井径流量换算的常用公式，它是根据裘布依公式导出。井径与涌水量的关系是比较复杂的，是目前尚未解决好的问题。

3实例演示

淮南某井田松散层中含抽水，含水层以中、细砂为主，厚度60.70 m，钻孔半径r=0.054 m，抽水试验资料如表1，简略评价含水层富水性。

3.1鉴别曲线类型

3.1.1伸直法

试验现场所作Q～S曲线，不是直线类型，而是三种曲线类型中的一种。分析整理抽水试验资料如表1，作S0=f(Q)，lgQ=f(lgS)和Q=f(lgS)三种曲线(图1)，从图1可以看出图1(b)最接近直线关系，为幂函数曲线类型。

3.1.2曲度法

所得：1

3.2确定待定系数

经鉴别抽水试验涌水量曲线类型为幂函数型，即,采用作图选点法和最小二乘法求取待定系数n、m值。

3.2.1作图法

3.2.2最小二乘法

涌水量曲线方程式可以写为

3.2.3验算

将抽水试验三次s值代入上式，求得Q1=11.61，Q2=15.1，Q3=18.84，与抽水试验三次涌水量相比较是接近的，采用最小二乘法计算是精准的。

3.3单位涌水量换算

经配型，抽水试验涌水量曲线类型为幂函数型，即

Q=4.7554S0.544

当降深为10 m时，涌水量为Q=16.64 L/s。

经计算口径为91 mm，降深为10 m时的单位涌水量为q=1.63 L/m·s，按此评价含水层的富水性为强富水性含水层。

(a)　　　　(b)　　　　(c)

原始资料降程S(m)Q(L/s)qS0lgSlgQ(lgS)2Q2(抛)lgSlgQ(幂)QlgS(对)15.1611.602.2480.44480.71261.06450.5079134.560.75868.266228.3615.141.8110.55220.92221.18010.8505229.21961.088313.9621312.5618.841.500.66671.0991.27511.2078354.94561.401320.7052∑45.582.73383.51972.5662718.72523.248242.9335

参考文献

[1]煤矿防治水规定.煤炭工业出版社.2009.

[2]煤矿床水文地质、工程地质及环境地质勘查评价标准.国家安全生产监督总局发布.2009.

[3]水文地质手册.地质出版社.1983.

[中图分类号]P641.4+1

[文献标识码]B

[文章编号]1004-1184(2016)02-0067-03

[作者简介]王灿(1982-)，男，安徽宿州人，工程师，主要从事水文地质与煤田地质勘探。

[收稿日期]2015-10-28