长筒袜压力分布预测非线性粘弹性有限元模型的建立

侯昀彤，　徐蓼芫，　王芳芳

(南通大学 纺织服装学院,江苏 南通 226019)



长筒袜压力分布预测非线性粘弹性有限元模型的建立

侯昀彤，徐蓼芫*，王芳芳

(南通大学 纺织服装学院,江苏 南通 226019)

摘 要：将人体作为粘弹体，以大腿截面为例，对其受到压力长筒袜束缚后的压力分布进行有限元建模。基于大腿股动脉止血点确定了大腿截面位置，使用三维人体扫描仪对样本腿部形态进行扫描，得到下肢大腿根部标准截面形态及标准曲线。根据标准曲线拟合出大腿根部截面曲线的二次方程。将得到的标准曲线导入ABAQUS软件中对大腿截面进行有限元建模，得到压力分布云图，预测压力分布的规律，并使用两款相似类型的压力长筒袜进行有限元模拟以验证预测模型的可信性。结果表明，在服装压力的研究中可以将人体视为粘弹体，建立的大腿截面非线性粘弹性有限元模型可有效地预测压力分布。该方法为建立下肢压力服装的压力预测模型提供了基础。

关键词：大腿截面；有限元；粘弹体；压力分布

目前,关于服装压力分布及预测的研究在国内外都已经取得了一定的成果。如张欣等[1-2]将人体视为刚性体，建立了动态服装压力分布的几何非线性数学模型；覃蕊等[3- 4]将人体假设为弹性体，对袜口处压力分布情况进行模拟分析。事实上目前大量的机械、生物力学[5-6]研究中，都将人体看作一个弹性特征和粘性特征兼具的粘弹体，而服装和人体之间的接触是弹性体与粘弹体之间的接触，属于粘弹性力学范畴[7]。而将人体简单地视为弹性体或者刚性体预测人体与服装之间的相对压力，得出相关的结论并不具有绝对的代表性。

建立人体的非线性粘弹性有限元模型能有效避免将人体直接认定为刚体或弹性体进行数学建模带来的相对误差。因此，文中将人体作为粘弹体，以大腿动脉止血点处的女性大腿截面为例，建立非线性的粘弹性有限元模型，模拟女性大腿受到压力袜束缚后的压力分布，并验证模型的可行性。

1建模准备

1.1大腿截面形态采集

因生存的气候、劳动生活习惯差异等外在因素，人体腿截面构造各不相同，腿型差异较大。考虑到研究成本、研究的普遍性及准确性，文中选取的人群总体样本为136个，依据统计样本设计方法(deff)[8]按简单随机抽样时，在90%置信度、绝对误差10%的情况下，抽样样本取总体比例的50%，故文中抽样样本应为68个。依据GB 10000— 1988《中国成年人人体尺寸》，选择136名年龄为22～25岁的女大学生作为样本，体质量为50～57 kg，身高160～167 cm，控制样本中女大学生的体质量及身高的平均数值分别与标准中90%的女性统计平均值接近。

同时，基于弹性力学中圣维南原理，研究分布于弹性体上一小块面积(或体积)内的荷载作用在物体上所产生的应力，荷载的具体分布只影响荷载作用区附近的应力分布[9]，故文中将大腿表面的压力按照大腿截面分割进行研究。为研究下肢服装压力与大腿动脉止血的关系，文中主要研究大腿动脉止血点处的截面曲线。将人体大腿朝外侧旋转展开，大腿股动脉的止血点就在腹股沟韧带中点向下两横指处[10](见图1)。一般在女性大腿根部向下2 cm的横截面上，即定义为本次的研究对象。

实验时，使用3D caMega光学三维人体扫描仪采集人体数据，扫描完整的三维人体。随后利用Geomagic Studio11软件处理扫描生成的人体云图，截取受试者右大腿内侧向下2 cm处的水平腿截面闭合曲线(见图2)。

1．2获取标准截面曲线

获取136个大腿截面曲线后，对所得符合要求的图形进行平均处理，以得到较为准确的大腿根部截面曲线。即在软件中将136条曲线同心叠加，将圆心为截取截面曲线时三维扫描系统自动定义的圆心，剔除其中明显不符合大腿基本形态的曲线和游离在集中区域外的曲线，即依次剔除距离圆心较远及较近的曲线。最终获取中间区域的68个截面曲线并导入MatLab7.0软件中处理。由于截面曲线为不规则的封闭曲线，为方便拟合截面曲线，将曲线分为8段拟合，每段至少10个点，以提高拟合曲线的相关系数。所以，以直角坐标系的Y轴正方向为基准，在68个截面曲线上顺时针每5°取一点，使用Matlab软件获取每个点的坐标。随机得到68组坐标值数据，将相同位置的68个点分别取平均值，从而得到标准截面曲线上72个点的平均坐标值。

以直角坐标系的Y轴正方向为基准，顺时针方向按每45°划分得8段曲线，通过观察，8段曲线均为连续光滑的抛物线形曲线，所以文中选择二次曲线拟合模型拟合曲线，确定函数：

y=a0+a1x+a2x2。

以0～45°曲线为例，拟合得二次曲线方程为

y=9.133 06+0.179 61x-0.088 65x2

(1)

R为拟合校正决定系数，决定系数R可以用于评价回归方程的优劣，但随着自变量个数的增加，R2将不断增大，R2越接近于1，曲线的拟合程度较高。依据公式：

(2)

计算可得该曲线R2为0.998 47，因此该曲线的拟合度较高。同理，依次计算拟合得到剩下7段曲线的二次曲线方程及R2(见表1)。

由表1可以看出，8段曲线的R2均在0.99之上，接近于1，故曲线的拟合度较高。由此可以得到大腿截面的标准曲线方程。

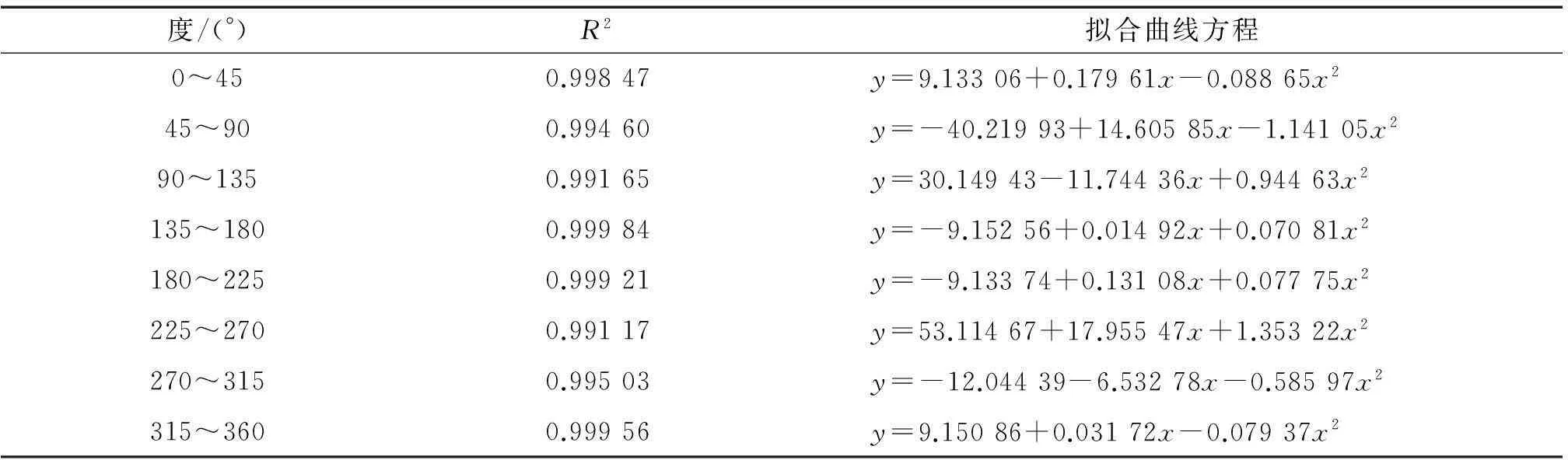
表1　大腿截面标准曲线拟合方程

1.3确定骨骼位置

由于骨骼的位置对大腿截面压力分布具有重要影响，为建立有效的压力预测有限元模型，在获取截面形态并建立方程的同时，还要获取大腿股骨的大体位置。文中使用25岁健康女性下肢组织的三维断层扫描图像数据(见图3)，使用Syngo FastView浏览器观测，获得大腿股骨在大腿截面中的坐标位置。

1.4压力测试

通过压力测试，预测有限元建模过程中所需设定的模型载荷大小。将选取的68名受试者随机分为A,B两组，在68人中随机选取60人为实验组A组，其余8人为对比组B组。A组中60名受试者均穿着市面上常见的压力袜(称为M款)，成分为80%锦纶和20%氨纶，两腿并拢，直立于地面，使用Novel pliance-X-32压力测试系统，以止血点所在位置为第一点，顺时针每45°一个点，为A组测试大腿截面上8个点的压力值，单位为kPa。

受试者虽然均为经过筛选的标准体，但身高、体重仍有差异，腿部的形状、粗细也有不同，故文中在获取A组60人的测试值后取均值，以保证实验数据的普遍性，减少实验误差。A组60人的压力测试均值见表2。由此预设定载荷大小，根据A组中60人的测试数据绘制如图4所示的压力正态分布曲线，大致可见8个测试点测试压力的最大值、最小值及均值的分布趋势。

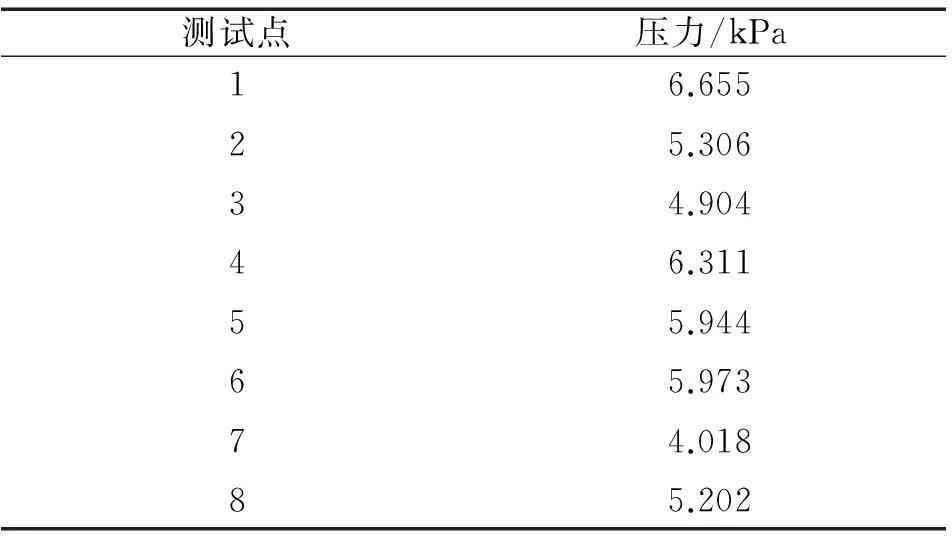
表2　A组压力测试均值

2大腿截面的仿真模拟

2.1大腿截面粘弹性组织结构模型的建立

文中将人体视为粘弹体，对其粘弹性进行有限元模拟。由于讨论的几个问题均属于典型的非线性问题，如载荷作用下大腿肌肉产生大位移和有限变形的几何非线性问题，服装与人体之间压力相互作用的接触非线性问题等。故文中利用软件ABAQUS Version 6.8-1，建立非线性粘弹性有限元模型，对压力袜与大腿截面的受力变形进行分析。

由于人体作为典型的粘弹体，具有明显的应力松弛特征，所以选择非线性粘弹性有限元模型中应力松弛模型对大腿截面模型进行有限元分析[11]。建模时粘弹性材料使用的应力函数通常以积分形式给出，本构方程如下：

(3)

式中：σ为Gauchy应力；G(t)为剪切松弛核函数；K(t)为体积松弛核函数；e为剪切应变；Δ为体积应变；t为当前时间；τ为过去时间；I为单位张量。

由于ABAQUS中，使用Prony级数表示粘弹性属性的本构方程，N为Prony级数的阶数，将式(3)转换后得本构方程的基本形式为

(4)

根据公式推导可以得到大腿截面建模中所需要的参数。虽然人体组织材料特性相对较为复杂，但大量的数据参数在国内外大量生物力学相关研究中已经得出，故文中参考其中已得的相关数据[12]，计算得到建模所需参数(见表3)。其中E为弹性模量。

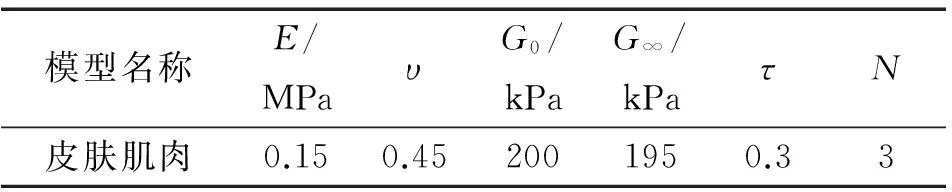
表3　粘弹性材料的相关参数

根据上文，将测量计算所得的大腿截面作为草图导入ABAQUS软件中，建立部件1，为大腿截面标注骨骼位置，建立部件2，为腿骨。部件1材料属性为粘弹性材料;部件2为弹性材料，股骨的弹性模量为7 300 MPa，泊松比0.3[12]。

依托部件1轮廓，建立部件3，为束缚在大腿表面的压力袜。将部件1、2、3装配，并指定材料属性。已知压力袜的主要成分包括80%锦纶和20%氨纶，弹性模量为935.56 MPa，泊松比0.401 3。

2.2有限元建模的接触分析及求解

在接触模拟中一般是基于表面的接触模拟或者是基于接触单元的接触模拟，彼此接触产生接触对，文中定义接触的本构模型为表面与表面的接触(surface)模型，分别建立皮肤与压力袜的接触对、皮肤与骨骼的接触对。为了加强收敛，建模过程中忽略骨骼与肌肉之间的摩擦以及服装与人体之间产生的摩擦力对模型的影响。

定义材料属性后对部件进行网络划分，尽可能减少计算资源的情况下，达到最高的单元质量。设置分析步为两步:①模拟压力袜静止时对大腿截面产生的压力;②模拟压力袜的拉伸活动对大腿截面的压力作用。载荷选择“压强”，施加载荷的表面为压力袜外表面，载荷大小为测试各点平均压强值中的平均值。

最后创建作业并求解，通过后处理得到大腿截面的应力分布云图(见图5)及预测压力值。

3验证及分析

3.1有限元建模结果分析

有限元模型的可信度是指在特定的条件下，模拟得到的有限元模型能够替代原始模型的可信性程度[13-14]。即保持输入条件一致，考察有限元模型的输出与实际测试结果的一致程度，从而验证模型的准确性。

此外，人体作为典型的具有粘弹性的生物组织结构，抗拉能力远比不上抗压能力。因此，文中采用对比平均等效应力的方式，验证模拟得到的有限元模型输出结果的正确性[15]，即通过有限元模型输出的应力结果与B组测试数据对比，评定模型的准确性。

由ABAQUS软件有限元建模得出的应力分布云图(见图5)中可见，图中内部曲线为受压后的应力分布等值曲线。图中应力大小从等值带a向等值带p递减，等值曲线反映了大腿截面受压后的变形趋势。

为验证预测压力分布有限元模型的准确性，在ABAQUS软件后处理中查询，获取与实际测试对应的8个点所在单元受到的应力大小。B组8名受试者的压力测试数据中随机抽取3组与有限元模型中预测得到的压力值进行验证，压力值见表4。

通过曲线拟合求得两组数据相似度R2分别为0.911，0.879和0.905。通常相似度越接近于1，数据的相似度越大。由表4可见，两组数据和预测数据的拟合相似系数R2均在0.9附近，接近于1，由此可见，预测数据与对比组数据相似度较高。

表4　压力值

3.2应用对比

为进一步验证预测模型的准确性，选择同类型压力袜(称为N款)进行测试与对比。N款压力袜的主要成包括90%锦纶和10%氨纶，厚度小于实验用压力袜，弹性模量为142.79 MPa，泊松比0.202 4。与M款压力袜实施同样的压力测试与有限元建模。令68名受试者中A、B两组成员分别穿上N款压力袜进行压力测试，测试要求及标准同上。测得的压力平均值见表5，并根据A组中60组数据绘制如图6所示的压力正态分布曲线。

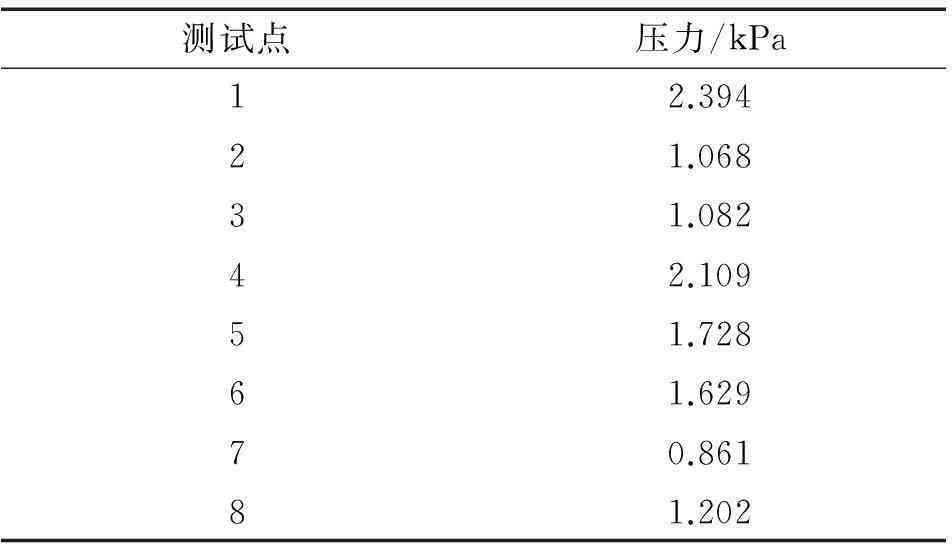
表5　A组压力平均测试值

对N款压力袜进行有限元建模，根据测试，将载荷设置为1.509 1 kPa，其余设置同上，求解后通过后处理得到如图7所示的大腿截面的应力分布云图及预测压力值。

对比两款压力袜的应力分布云图可以看出，图7中应力分布等值曲线的分布规律与图5相似。图中应力大小均从等值带a向内递减，大腿截面受压后的变形趋势亦相似。

在后处理中查询获取N款压力袜的8个测试点所在单元受到的应力大小。同样从B组受试者中随机选取3人的压力测试数据与有限元模型中预测得到的压力值进行验证，压力值见表6。通过曲线拟合求得3组数据相似度R2分别为0.913，0.893和0891，均在0.9附近，接近于1。可见，预测数据与对比组数据相似度较高。

表6　压力值

绘制如图8所示两款压力袜的预测压力值曲线。曲线拟合求两组预测数据的相似度，求得相似度R2为0.866。由此可见，两组预测压力值的分布趋势相似，压力预测模型准确性较高。因此可以说明，将人体视为粘弹体建立的非线性粘弹性有限元模型具有一定的准确性，建立的压力预测模型预测得到的数据具有较高的可信度，可以用以预测压力袜对大腿截面产生的束缚压力的分布情况。

4结语

文中将人体视为粘弹体，通过三维人体扫描仪得到了人体大腿动脉止血点向下2 cm处大腿截面形态及方程。基于大腿标准截面曲线的数学模型，运用ABAQUS软件建立非线性粘弹性有限元模型，预测压力分布，验证并得出结论：基于人体为粘弹体建立的非线性粘弹性有限元模型，模拟得到的应力分布规律与测试压力分布基本一致，可用于预测大腿截面曲线上的压力分布，并可以依次类推，由线及面，获得整个大腿表面的压力分布。故在服装压力的研究中，可以将人体视为粘弹体，非线性粘弹性有限元模型的建立可以用于下肢医用及紧身服装压力分布预测模型，为建立有效的服装压力与下肢动脉止血之间关系的数学模型提供了数据参考和理论依据。

参考文献：

[1] ZHANG Xin,YEUNG K W,LI Yi.Numerical simulation of 3D dynamic garment pressure[J].Textile Research Journal,2002,72(3):245-252.

[2] WONG A S W,LI Yi,ZHANG Xin.Influence of fabric mechanical property on clothing dynamic pressure distribution and pressure comfort[J].Fiber,2004,60(10):293-299.

[3] 覃蕊,范雪荣,陈东生,等.男短袜袜口压力的有限元研究[J].纺织学报,2011,32(1):105-110.

TAN Rui,FAN Xuerong,CHEN Dongsheng,et al.Study on pressure at top part of man's socks using finite element method[J].Journal of Textile Research,2011,32(1):105-110.(in Chinese)

[4] 覃蕊,范雪荣,陈东生.男短袜袜口处标准腿截面曲线研究[J].纺织学报,2012,33(3):119-123.

TAN Rui,FAN Xuerong,CHEN Dongsheng.Study on standard curve of lower leg cross section at top of men's socks[J].Journal of Textile Research,2012,33(3):119-123.(in Chinese)

[5] 张琳琳,沈凌,朱明,等.大腿残肢步态过程的非线性有限元分析[J].医用生物力学,2013,28(4):397- 402.

ZHANG Linlin,SHEN Ling,ZHU Ming,et al.Non-linear finite element analysis on trans-femoral residual limb during gait phase[J].Journal of Medical Biomechanics,2013,28(4):397- 402.(in Chinese)

[6] 穆晨,钱秀清,闫松华,等.预应力下大腿残肢站立中期时相的有限元分析[J].医用生物力学,2011,26(4):321-324.

MU Chen,QIAN Xiuqing,YAN Songhua,et al.Finite element analysis of interface pressure over the above-knee residual limb at mid stance phase with pre-stress[J].Journal of Medical Biomechanics,2011,26(4):321-324.(in Chinese)

[7] 许政,王庆,付志一.粘弹性体接触时接触应力的有限元法分析[J].石河子大学学报(自然科学版),2002,6(4):324-326.

XU Zheng,WANG Qing,FU Zhiyi.Finite element analysis of contact stress on viscoelastic contact[J].Journal of Shihezi University(Natural Science),2002,6(4):324-326.(in Chinese)

[8] 徐静远.抽样调查中样本量的确定[J].统计与咨询,2009(4):43.

XU Jingyuan.Determination of sample size in survey sampling[J].Statistics and Consulting.2009(4):43.(in Chinese)

[9] 黄乘规.关于圣维南原理的一点注释[J].力学学报,1981(1):101-104.

HUANG Chenggui.A note on the Saint Venant principle[J].Journal of Mechanics,1981(1):101-104.(in Chinese)

[10] 姚家琪.人体动脉解剖模式图谱:正常及变异[M].2版.北京:人民卫生出版社,1998:134.

[11] 高秀华,张小江,王欢,等.有限单元法原理及应用简明教程[M].北京:化学工业出版社,2008:138.

[12] Bosboom E M,Hesselink M K,Oomens C W,et al.Passive transverse mechanical properties of skeletal muscle under in vivo compression[J].Journal of Biomechanics,2001,34(10):1365-1368.

[13] 柳世考,刘兴堂,张文.利用相似度对仿真系统可信度进行定量评估[J].系统仿真学报,2002,14(2):143-145.

LIU Shikao,LIU Xingtang,ZHANG Wen.Quantitative assessment of the reliability of simulation system by using the similarity[J].Journal of System Simulation,2002,14(2):143-145.(in Chinese)

[14] LI Jin,LIU Hao,WANG Yuxiu,et al.Development of a low cost portable pressure measurement system using for garment design[J].Measurement,2012,45:2114-2120.

[15] Naokazu Miyamoto,Yasuo Kawakami.Effect of pressure intensity of compression short-tight on fatigue of thigh muscles[J].The American College of Sports Medicine,2014:2168-2171.

(责任编辑：邢宝妹)

Pressure Distribution Analysis of Stockings by a Nonlinear Viscoelastic Finite Element Model

HOU Yuntong,XU Liaoyuan*,WANG Fangfang

(School of Textile and Clothing,Nantong University,Nantong 226019,China)

Abstract：Takeing the pressure distribution of the thigh cross section which is bounded by compression stockings,has been studied by finite element modeling in this paper. Taking the human body as a viscoelastic body,by comfirming the thigh section according to the thigh artery bleeding point and scanning the morphological characteristics of sample' legs by 3D body scanner the standard cross section shape and curve of lower thigh root are obtained.Then the quadratic equation of thigh root's section curve is established according to the standard curve.The standard curve has been imported into ABAQUS software to get the finite element model of thigh section and the pressure distribution nephogram,which predictes the pressure distribution principle.Finally,the credibility of the prediction model has been verified by finite element simulation with two similar types of stockings.Conclusion:The human body can be regarded as a viscoelastic body in the research of clothing pressure.So that it is effective to predict the pressure distribution by setting up a nonlinear viscoelastic finite element model of thigh cross section,which establishes the theoretical basis for building a prediction model of pressure distribution applied to lower limb compression garment.

Key words:leg cross section，finite element model,viscoelastic,pressure distribution

中图分类号：TS 941.7

文献标志码：A

文章编号：2096-1928(2016)01-0046-07

作者简介：侯昀彤(1991—)，女，硕士研究生。*通信作者：徐蓼芫(1957—)，女，副教授，硕士生导师。主要研究方向为服装人体工效学、服装压力舒适性等。Email：xu.ly@ntu.edu.cn

基金项目：江苏省普通高校研究生科研创新计划项目(KYLX_1309)；南通大学纺织服装学院研究生自主创新项目(fz201304)。

收稿日期：2015-10-15；

修订日期：2015-12-05。