枢纽多级容量限制下辐点分配模式的比较
2016-05-22尹宇起胡志华
杨 斌,尹宇起,胡志华
(上海海事大学 物流研究中心,上海 201306)
枢纽多级容量限制下辐点分配模式的比较
杨 斌,尹宇起,胡志华
(上海海事大学 物流研究中心,上海 201306)
针对轴辐式网络中辐点的单分配和多分配模式的现实差异,提出枢纽多级容量限制下的辐点分配模式的比较问题,研究需求不确定条件下两种分配模式的特点。基于轴辐式网络设计的基本模型,构建枢纽多级容量限制下考虑运营成本的两种分配模式的混合整数规划模型。根据预测的多个需求场景及其概率分布求解两种网络模型的最优期望成本以设计轴辐式网络。通过设置网络最优设计、预先给定枢纽点数目和总需求量变动3项实验,比较辐点的单分配和多分配模式在各实验结果中的网络成本、枢纽配置和枢纽利用率,发现多分配网络具有较低的网络总成本、较少的枢纽数目及较高的枢纽利用率。
交通运输工程;单分配;多分配;轴辐式网络;多级容量限制;需求不确定性
在轴辐式网络中辐点的分配模式包括单分配和多分配,其中,辐点的单分配模式被广泛地应用于航空、快递等运输网络的研究[1-3]中。简化模型及突出问题特点是研究者选择单分配模式的主要原因,然而单分配模式可能并非网络设计的最优选择。笔者将对枢纽多级容量限制条件下辐点的单分配和多分配模式进行比较。
枢纽点的容量限制影响枢纽点配置及辐点分配。在轴辐式网络中,枢纽点的建设需要投入一定的建设成本,并且由于建设成本及选址区位的限制,枢纽点有限的设施和设备限制了自身的处理能力。轴辐式网络中OD(origin destination)流的运输都要经过一个枢纽点或一条干线,因此枢纽点处理能力会影响其覆盖的辐点范围。相对于无容量限制的网络而言,满足相同客户的收集、运输和配送需求,具有容量限制的网络就需要更多的枢纽点。
由于干线运输的规模效应是轴辐式网络的利润源头,OD流的不确定性成为网络设计的关键。虽然可以通过预测得到网络的需求,但是市场经济波动环境下的OD流需求具有波动性。笔者在网络设计时考虑多种需求场景及其出现概率,采用求解多场景下网络的最优期望成本的策略进行网络设计,以弥补不确定性的影响。
在枢纽点容量限制的情况下,比较两种模式选择最优网络设计时的网络成本、枢纽配置、枢纽利用率。预先确定枢纽点数目,求解并比较此时网络的成本、枢纽配置、枢纽利用率。通过改变OD流需求,比较两种模式在需求变动中的稳定性。同时,对多分配网络设计中的单位运营成本的敏感性进行了讨论。通过进行算例仿真实验,发现多分配模式的网络总成本总是比单分配模式网络的总成本低,并且运营成本占网络总成本比例较低时单位运营成本的变动对网络设计没有影响。多分配网络中枢纽的利用率较高,而且当OD流需求总量有变化时多分配网络稳定性更高,但是多分配网络比单分配网络更复杂,货流的调度更加困难。
1 轴辐式网络
辐点的分配方式是轴辐式网络设计的一个重要方面,其主要考虑两种模式:单分配模式和多分配模式。单分配轴辐式网络[4-10]中一个辐点只能分配给一个枢纽点;多分配轴辐式网络[11-18]中一个辐点可以分配多个枢纽点。倪玲霖等[19]认为由于多分配网络可以根据快递量灵活分配中转枢纽,因此比单分配网络具有更加优越的性能。但是文献并未对多分配网络的优越性及网络的经济成本进行研究,缺乏理论基础。单分配与多分配网络[20-24]的研究主要集中于对两种分配模式的模型与算法的研究,并未涉及两种模式优劣的比较。
枢纽点的建设成本是网络总成本重要组成本部分,且枢纽点的容量不可能是没有限制的,为了适应网络的整体规划,笔者考虑枢纽点的多级容量限制。I.CONTRERAS等[25]考虑了单分配问题的枢纽点容量限制,并且利用拉格朗日松弛放松枢纽点容量限制,使其模型能够处理较大规模的算例。I.CORREIA等[26]针对有容量限制的单分配枢纽选址问题,考虑枢纽点的流量均衡,在已有的混合整数规划模型的基础上,提出了改进的混合整数规划模型,并且验证改进模型具有更优越可计算性,然而文献并未考虑节点间流量的不确定性。
轴辐式网络设计中准确地预测OD流需求是困难的。胡青蜜等[27]针对确定性OD流需求的零担物流网络设计方案往往导致网络资源非均衡利用问题,分析了零担物流节点之间OD流不确定性特点与不确定OD流需求的物流网络设计难点,结合库存理论,建立了不确定OD流需求的物流网络混合整数规划模型。S.A.ALUMUR等[28]针对选址问题的战略决策特性,在轴辐式网络设计的模型基础上,提出了考虑OD流需求和建设成本不确定性的单分配和多分配的轴辐式网络设计模型,并验证模型的可行性。I.CONTRERAS等[29]等研究了具有随机不确定性需求与运输成本的无容量限制枢纽位置问题。笔者在以上研究的基础上,考虑了在不确定OD流需求情况下枢纽点的多级容量限制,通过求解最优期望成本得到最优的网络设计,包括枢纽配置和辐点分配,比较单分配与多分配网络的优劣。
2 问题定义
2.1 问题概述
笔者研究的轴辐式网络是二层轴辐网络,其中,枢纽点承担货流的收集、分配和转运功能,辐点被分配给枢纽点。单分配模式指任一辐点只能被分配给一个枢纽点;多分配模式指任一辐点可以被分配给r(r≥1)个枢纽点。分配模式影响着网络的运营成本,相对于单分配的网络来说,多分配的网络中辐点的货物需要分批地运送到不同的枢纽点,同样,货物在枢纽点需要更多次数的分拣,这些活动都会增加网络的运营成本。为了体现不同分配模式间运营成本的差异,笔者定义比例系数α(α>1)表示多分配模式单位运营成本与单分配模式单位运营成本的比例。
不论如何选择辐点分配方式,枢纽点容量限制都会影响枢纽点的配置及辐点的分配。在多级枢纽点容量限制的情况下,枢纽点的配置包括枢纽节点的选择和枢纽点容量等级的选择。对同一节点而言,其建设为枢纽的投入与其所选择的容量等级有关,因此灵敏的建设成本成为网络设计模型的重点。
OD流需求的不确定性增加了网络设计的难度,增加了枢纽节点及其容量的等级选择的困难,难以合理地分配辐点。为应对季节性、市场的波动造成的需求不确定性,考虑多种需求场景并确定相应的概率分布,通过求解多场景下的最优期望成本,确定枢纽点的配置和辐点的分配。
基本模型[28]是枢纽无容量限制、完全干线网络的单分配和多分配轴辐式网络模型,在此基础上分别建立枢纽有容量限制的网络模型。
首先,基本模型([M1]和[M2],见第3.1节)的目标函数包括建设成本、集散成本及转运成本3个部分。其中建设成本是某一节点被选为枢纽点后需要投入的枢纽建设成本,集散成本是指枢纽点与辐点间货物收集和配送的运输成本,转运成本是指枢纽点间的转运货物的运输成本。
然后在基本模型上增加运营成本以突出单分配与多分配的差异。考虑枢纽点的多级容量限制更新约束及变量,按照不确定需求的处理方法,改进目标函数,最终得到枢纽多级容量限制下的单分配与多分配的轴辐式网络比较问题的扩展模型([M3]和[M4],见第3.2小节)。
2.2 问题假设和符号定义
笔者所研究的轴辐式网络包括单分配和多分配两种模式,其中,干线网络是全连通网络,网络节点间的距离满足三角不等式准则,每一个辐点只与枢纽点相连,辐点间无直接联系,枢纽点的处理能力有多级容量限制。
2.2.1 集合与索引
N={1,2,…,LN}为节点集合,由i,j,k和l索引;Q={1,2,…,LQ}为枢纽点容量状态集合,由q索引;S={1,2,…,LS}为需求状态场景集合,由s索引。
2.2.2 参 数

2.2.3 变 量
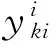
3 模 型
在基本模型上扩展得到的轴辐式网络设计模型([M3]和[M4])。由于在扩展的过程中存在约束条件等的变化,下面在给出模型的同时也将对其中相应的约束进行阐述。
3.1 基本模型
3.1.1 单分配轴辐式网络设计的基本模型
[M1]:
minftotal=fsetup+fcd+ftran
(1)
fsetup=∑kfkxkk
(2)
fcd=∑i,kλ·(Oi+Di)Dikxik
(3)
(4)
s.t.∀i∈N,∑k∈Nxik=1
(5)
∀i,k∈N,xik≤xkk
(6)
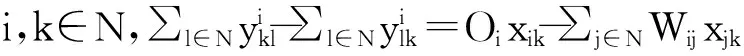
(7)

(8)

(9)
∀i,k∈N,xik∈{0,1}
(10)
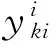
3.1.2 多分配轴辐式网络设计的基本模型
[M2]:
minftotal=fsetup+fcd+ftran
(11)
式[(2),(4)]
(12)
s.t.∀i∈N,∑k∈Nuik=Oi
(13)

(14)

(15)
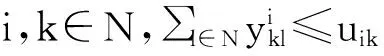
(16)
∀i,k∈N,uik≤xkkOi
(17)
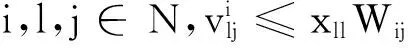
(18)
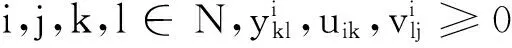
(19)
∀k∈N,xkk∈{0,1}
(20)
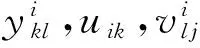
3.2 扩展模型
通过变换目标和约束得到[M3]和[M4],其中枢纽存在多级量限制且考虑了OD货流需求的不确定性,下面更新某些变量。
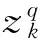
3.2.1 枢纽多级容量限制的单分配轴辐式网络设计
[M3]:
minftotal=fsetup+∑s(fcd+ftran+fope)Ps
(21)
(22)
(23)
(24)
(25)
s.t. 式[(5)~(6),(10)]
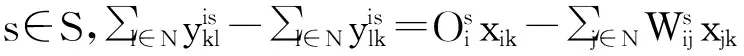
(26)
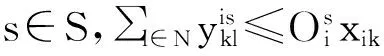
(27)
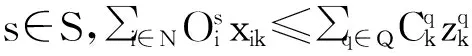
(28)
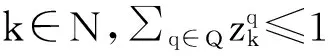
(29)
(30)
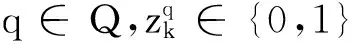
(31)
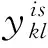
3.2.2 枢纽多级容量限制的多分配轴辐式网络设计
[M4]:
minftotal=fsetup+∑s(fcd+ftran+fope)Ps
(32)
式[(22),(24)]
(33)
(34)

(35)
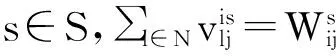
(36)
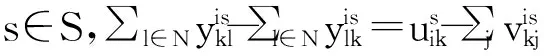
(37)

(38)
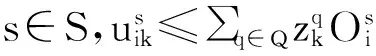
(39)

(40)
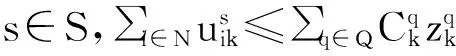
(41)

(42)
(43)
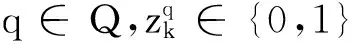
(44)
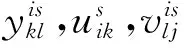
4 仿真实验
考虑20个节点(LN=20)的轴辐式网络,其中,枢纽点容量限制有3个等级(LQ=3),需求场景有3种(Ls=3)。为了求解混合整数规划模型,在仿真实验中采用MATLAB编写代码调用CPlEX求解器进行求解。针对单分配与多分配轴辐式网络基础模型([M1]&[M2])分别编写基础代码,然后在基础代码基础上根据实验设置及改进模型要求修改得到其他模型代码,最后应用算例数据进行实验。
4.1 基本算例
对于模型中的参数,设置λ=1,ω=0.7,ν=1。两种模式的单位运营成本比例系数α=1.5。在[M3]和[M4]中节点选为枢纽时在实验中多级容量限制的值为[15 000,20 000,25 000],并且第一容量限制等级的枢纽建设成本由均匀分布α=U[10 000,50 000]生成,则各级成本按照[a,1.25a,1.5a]方式处理。
实验中节点的位置坐标由(U[0,120],U[0,120])均匀分布生成。OD流值状态场景概率随机取自区间[0,1]。其状态场景划分为:场景1为节点货流需求量在某区间大范围波动,货流不稳定的情形;场景2为节点货流需求量在某区间小范围波动,货流较稳定的情形;场景3为节点具有货流低需求量或货流高需求量的情形。例如,表1中枢纽点3到枢纽点4的OD流值在场景1下OD流值随机取自区间[100,200],场景2下OD流值随机取自区间[120,150],场景3下OD流值取自区间[170,200]。

表1 生成需求场景的数据表
表1中集合A1表示除节点4,5,12,18以外的其他任意节点,例如始发点为节点3时,A1={1,2,6,7,8,9,10,11,13,14,15,16,17,19,20},集合A2,A3同理。
4.2 实验设置及实验结果
为了求解[M3]与[M4]的实验结果以及比较二者之间的差异选择较优的分配模式,笔者设置了4个实验。
4.2.1 实验1
实验目的:比较最优网络总成本及其中各部分成本构成、网络设施资源的利用率,探究两种网络的特性。
实验过程:①枢纽点数目不限制,对[M3]和[M4]进行实验;②采用4.1小节生成的数据及参数。
统计实验结果得网络总成本及各部分成本,如图1。枢纽点配置及实际利用情况,如表2及图2。
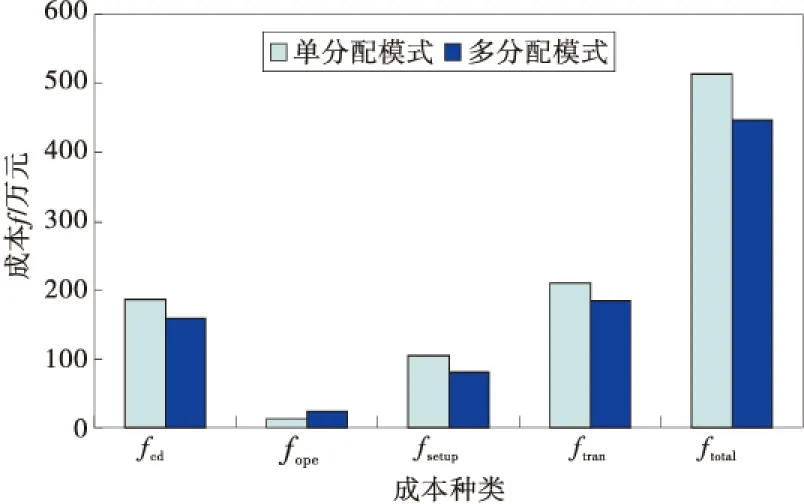
图1 成本对比Fig.1 Comparison of costs
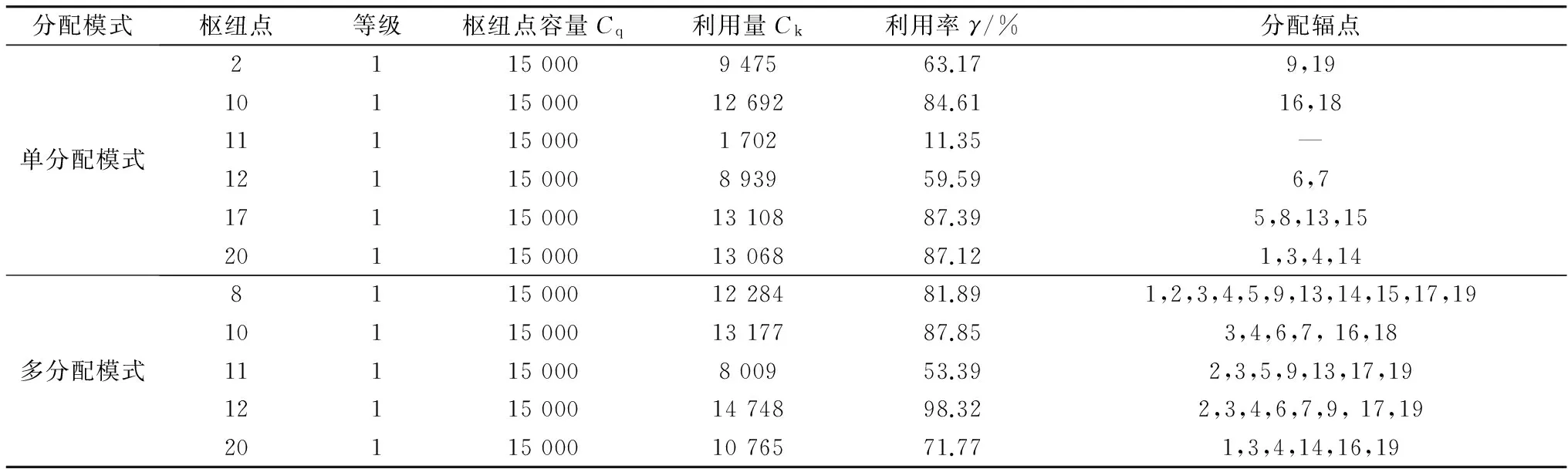
分配模式枢纽点等级枢纽点容量Cq利用量Ck利用率γ/%分配辐点单分配模式2115000947563.179,19101150001269284.6116,1811115000170211.35—12115000893959.596,7171150001310887.395,8,13,15201150001306887.121,3,4,14多分配模式81150001228481.891,2,3,4,5,9,13,14,15,17,19101150001317787.853,4,6,7,16,1811115000800953.392,3,5,9,13,17,19121150001474898.322,3,4,6,7,9,17,19201150001076571.771,3,4,14,16,19

图2 最优网络布局Fig.2 Optimum network layout
4.2.2 实验2
实验目的:参数α的敏感性分析。
实验过程:①枢纽点数目不限制,对[M3]和[M4]进行实验;②按照-75%,-50%,-25%,25%,50%,75%调节参数α大小。
实验结果如表3。
表3 参数α的敏感性分析实验结果
Table 3 Experiment results of sensitivity analysis of parameterα/%
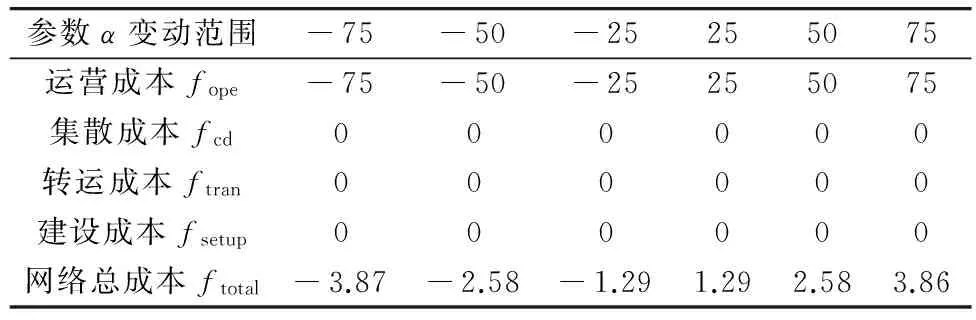
参数α变动范围-75-50-25255075运营成本fope-75-50-25255075集散成本fcd000000转运成本ftran000000建设成本fsetup000000网络总成本ftotal-3.87-2.58-1.291.292.583.86
4.2.3 实验3
实验目的:预先确定枢纽点数目情况下,比较两种模式的优劣。
实验过程:①增加约束条件,调整后的模型,如[M5]与[M6];②确定枢纽点数目P=3,4,5,6,7,分别对[M5]和[M6]进行实验。
[M5]:
minftotal=fsetup+∑s(fcd+ftran+fope)Ps
(45)
s.t. 式(22)~(31)

(46)
[M6]:
minftotal=fsetup+∑s(fcd+ftran+fope)Ps
(47)
s.t. 式[(22),(24),(33)~(44),(46)]

实验结果如表4,图3、图4。

表4 枢纽配置
注:括号内为枢纽等级
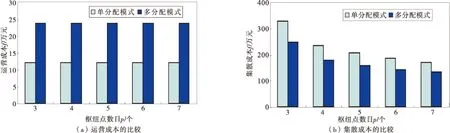
图3 各项成本比较Fig.3 Comparisons of various costs
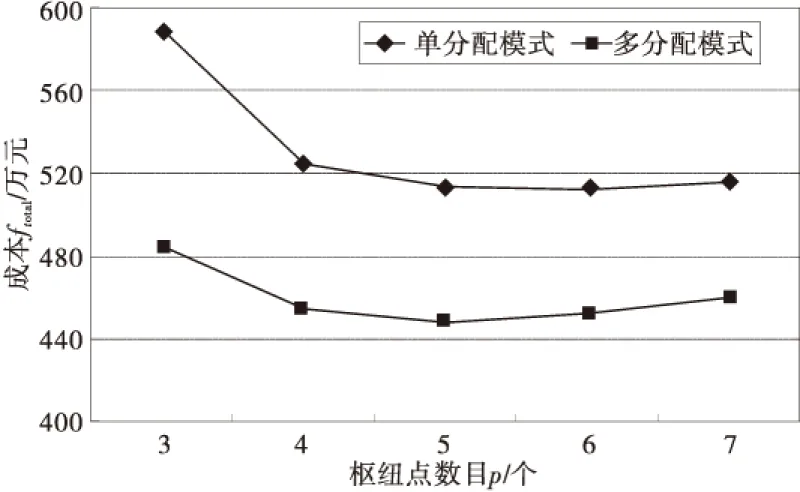
图4 枢纽数目P=3,4,5,6,7的网络总成本Fig.4 Total network costs with the number of hub P=3, 4,5,6,7
4.2.4 实验4
实验目的:在OD流变动的情况下,比较两种网络模式的稳定性。
实验过程:①由场景2生成一组新的OD流需求数据,并且生成其100%,120%,140%,160%倍的一系列数据;②其他参数不变,对每组进行实验。
实验结果如图5、图6,及表7。
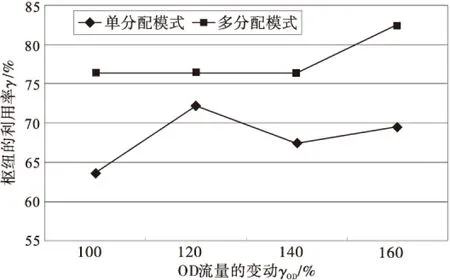
图5 新OD流场景下枢纽的利用率变动Fig.5 Utilization rate changes of hub in new OD flow scenarios
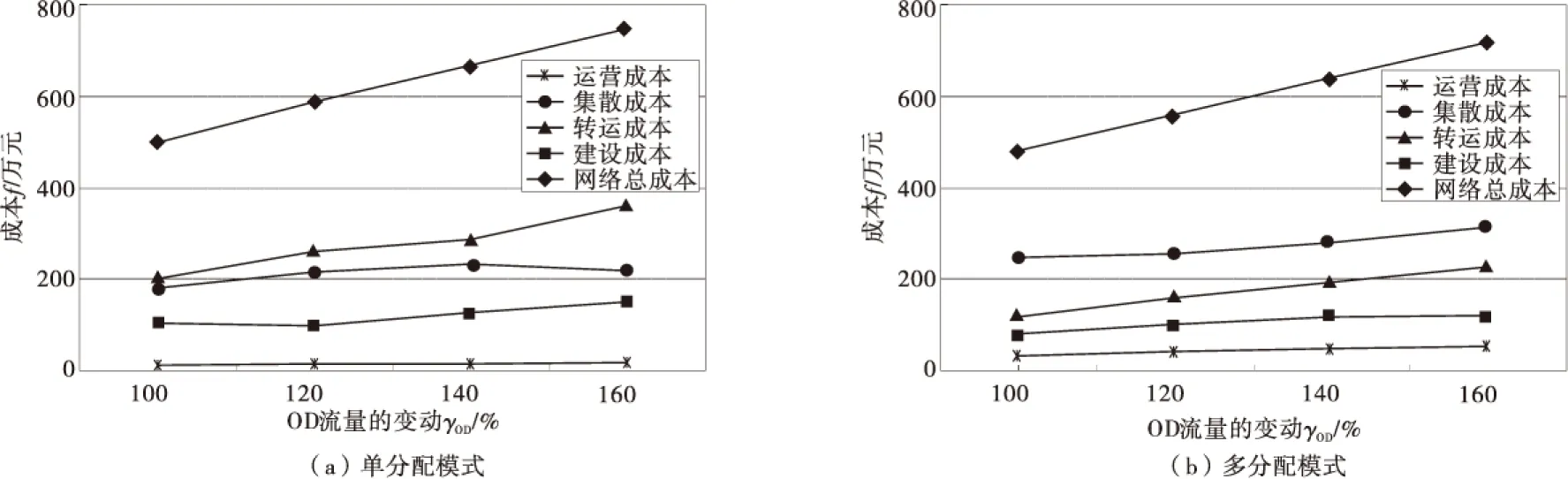
图6 新OD流场景下的成本变动Fig.6 Costs changes in new OD flow scenarios

需求增加比例ΔγOD/%单分配模式枢纽配置多分配模式枢纽配置02(1),10(1),11(1),12(1),17(1),20(1)8(1),10(1),11(1),12(1),20(1)202(1),8(1),10(2),11(1),12(1),20(1)2(1),10(1),11(1),12(1),17(1),20(1)401(1),2(1),10(2),11(1),12(1),17(2),20(1)1(1),2(1),10(1),11(1),12(1),17(1),20(1)601(1),2(1),8(1),10(3),11(1),12(1),17(1),20(1)1(1),2(1),10(2),11(1),12(1),17(1),20(1)
注:括号内为枢纽等级。
4.3 实验分析
下面对4.2小节中4个实验的结果进行分析:
实验1中,由图1中两种分配模式的各项成本对比可以清楚地看出,建设最优的轴辐式网络时,单分配轴辐式网络的建设成本、运输成本明显高于多分配网络的相应成本;由表4、表5可知,单分配网络所需要的枢纽数量多于多分配网络,而且由公式枢纽的平均利用率=(∑i枢纽i的利用率)/(枢纽个数)可得,单分配网络枢纽的平均利用率为65.54%低于多分配网络枢纽的平均利用率(78.64%)。然而,多分配网络中枢纽点辐射的辐点个数远多于单分配网络的。
在多分配轴辐式网络中,辐点分配约束的取消使得集散运输过程的隐含成本释放出来,也使得网络枢纽设施的利用率有所提高,而且枢纽利用率的提高可以减少枢纽点的建设数目,确保了核心节点(例如节点10,其在两种模式中同时存在且具有较高的利用率)的规模效应。然而,多分配网络的缺点就像图2中情况一样,不仅增加了运营成本,而且网络复杂、网络流混乱、货物分拣频繁和调度困难。
由实验2可知,在多分配轴辐式网络中,运营成本占网络总成本的比例较小。当单位运营成本(α)变动时,网络总成本只产生轻微的变动,而且枢纽点的配置和辐点的分配并未发生变化,总成本的变动只与运营成本有关。因此,当运营成本占网络总成本的比例较小时,α的变动并不会影响辐点的分配和枢纽点的配置。
实验3中枢纽点数目的变化并未改变单分配轴辐式网络的高成本特点。由图3可知,随着枢纽点的增加,干线网络的规模效应减弱,而支线的集散成本减少,最终使得两种模式网络总成本的变化趋势具有一定的相似性。然而在枢纽点数目的变化过程中,存在某些“职业枢纽”的节点——始终被选择为枢纽的节点,例如单分配模式下的节点10和节点17、多分配模式下的节点10,笔者把这种节点称为核心节点。核心节点不仅是“职业枢纽”,而且具有较高的利用率。这种高利用率表明节点具有较高的效益,同样,表明节点在网络中具有较大权重,相对于普通节点而言,当核心节点由于管理等原因失效时,正常的网络流会受到较大的冲击。因此,在确定枢纽数目的网络设计中,核心节点是轴辐式网络管理的重点,而且单分配网络中核心节点的比重较大。
从成本的角度看,OD流需求的增加会引起网络总成本的增加,且两者存在近似线性的变动关系;多分配网络的总成本依旧低于单分配网络的总成本,而且多分配网络总成本的变化趋势略缓,这与实验1中分析的多分配网络特性有关;枢纽点配置能够对建设成本与转运成本产生相同影响。从枢纽利用率的角度看,由于单分配网络中存在辐点分配约束,当OD流需求增加时,网络中枢纽的平均利用率分布较为离散。从枢纽点的配置角度看,OD流需求的增加导致网络中枢纽点数目的增加、枢纽等级的提高;需求量的变动过程中,多分配网络中枢纽配置表现得更稳定,其中核心节点的作用更突出。
综合以上分析,比较两种模式轴辐式网络,多分配网络的成本更经济,并且运营成本的变动不会影响网络中枢纽点的配置;多分配网络中由枢纽点组成的干线网络相对简单,枢纽点的平均利用率较高;多分配网络中枢纽点辐射的辐点数目过多导致网络复杂,并且同一OD流的货物被分批零散地运输导致货流调度的困难;在OD流需求的变动过程中,多分配网络的稳定性更高,而且枢纽的利用率波动较少。
5 结 语
选择不同的辐点分配方式,二级轴辐式网络将被分为单分配轴辐式网络和多分配轴辐式网络。在考虑枢纽多级容量限制的情况下,笔者对两种网络模式进行对比研究,提出了枢纽多级容量限制下单分配与多分配的轴辐式网络的比较问题。为了处理OD流需求的波动性,采用多个需求场景并确定需求场景的概率分配,通过求解网络最优期望成本以实现网络设计的要求。首先,选择单分配和多分配的轴辐式网络设计基本模型;然后,基于基础模型,分别建立关于单分配与多分配的OD流需求不确定情况下考虑枢纽多级容量限制的网络设计模型。为了比较单分配与多分配的优劣,笔者进行了以下对比实验:
1)比较两种模式选择最优网络设计时的网络成本、枢纽配置、枢纽利用率。
2)预先确定枢纽点数目,求解并比较此时网络的成本、枢纽配置、枢纽利用率。
3)通过改变OD流需求,比较两种模式在需求变动中的稳定性。
同时,笔者也对多分配网络设计中的单位运营成本的敏感性进行了讨论。通过进行算例仿真实验,发现多分配模式的网络总成本总是比单分配模式网络的总成本低,并且运营成本占网络总成本比例较低时单位运营成本的变动对网络设计没有影响;多分配网络中枢纽的利用率较高、建设成本较低有利于网络的快速建成,而且当OD流需求总量有变化时多分配网络稳定性更高;然而,多分配网络比单分配网络更复杂,货流的调度对节点企业来说是较大的考验。笔者的模型和分析将拓展到实际零担物流和航空运输网络的优化,进行验证和修正;考虑到模型求解的复杂性,将研制适应大规模轴辐式网络中环保多车型策略分析的算法。
[1] 倪玲霖, 史峰, 方晓平,等. 全连通快递网络与轴辐快递网络的比较[J].系统工程, 2009, 27(12): 45-50. NI Linglin, SHI Feng, FANG Xiaoping,et al. Comparative study on fully-connected and hub-and-spoke express operational network[J].SystemsEngineering, 2009,27(12):45-50.
[2] 杨忠振, 陆婧. 轴-辐式机场长途巴士线网运营时刻表优化设计[J]. 系统工程理论与实践, 2012, 32(9): 2050-2056. YANG Zhongzhen, LU Jing. Optimization of the timetable for a hub-spoke airport coach network[J].SystemsEngineering-Theory&Practice, 2012, 32(9): 2050-2056.
[3] ADLERA N,SMILOWITZB K. Hub-and-spoke network alliances and mergers: price-location competition in the airline industry[J].TransportationResearchPartB:Methodological, 2007,41(4):394-409.
[4] ABDINNOUR-HELM S. A hybrid heuristic for the uncapacitated hub location problem[J].EuropeanJournalofOperationalResearch,1998,106(2/3):489-499.
[5] ERNST A T, KRISHNAMOORTHY M. Efficient algorithms for the uncapacitated single allocation p-hub median problem[J].LocationScience,1996,4(3):139-154.
[6] ERNST A T,KRISHNAMOORTHY M. Solution algorithms for the capacitated single allocation hub location problem[J].AnnalsofOperationsResearch,1999,86(1):141-159.
[7] LABBé M, YAMAN H. Projecting the flow variables for hub location problems[J].Networks,2004,44(2):84-93.
[8] LABBé M, YAMAN H, GOURDIN E. A branch and cut algorithm for hub location problems with single assignment[J].MathematicalProgramming,2005,102(2):371-405.
[9] PIRKUL H,SCHILLING D A. An efficient procedure for designing single allocation hub and spoke systems[J].ManagementScience,1998,44(12):235-242.
[10] SKORIN-KAPOV D, SKORIN-KAPOV J. On tabu search for the location of interacting hub facilities[J].EuropeanJournalofOperationalResearch,1994,73(3):502-509.
[11] BOLAND N, KRISHNAMOORTHY M, ERNST A T, et al. Preprocessing and cutting for multiple allocation hub location problems[J].EuropeanJournalofOperationalResearch,2004,155(3):638-653.
[12] CONTRERAS I, FERNNDEZ E, MARN A. Tight bounds from a path based formulation for the tree of hub location problem[J].Computers&OperationsResearch,2009,36(12):3117-3127.
[13] CONTRERAS I, CORDEAU J F, LAPORTE G. Benders decomposition for large-scale uncapacitated hub location [J].OperationsResearch,2011,59(6):1477-1490.
[14] EBERY J, KRISHNAMOORTHY M, ERNST A, et al. The capacitated multiple allocation hub location problem: formulations and algorithms[J].EuropeanJournalofOperationalResearch,2000,120(3):614-631.
[15] ERNST A T, KRISHNAMOORTHY M. Exact and heuristic algorithms for the uncapacitated multiple allocation p-hub median problem[J].EuropeanJournalofOperationalResearch,1998,104(1):100-112.
[16] HAMACHER H W, LABBÉ M,NICKEL S. Adapting polyhedral properties from facility to hub location problems[J].DiscreteAppliedMathematics,2004,145(1):104-116.
[18] MAYER G, WAGNER B. Hub locator: an exact solution method for the multiple allocation hub location problem[J].Computers&OperationsResearch,2002,29(6):715-739.
[19] 倪玲霖, 史峰.多分配快递轴辐网络的枢纽选择与分配优化方法[J].系统工程理论与实践,2012,32(2):441-448. NI Linglin, SHI Feng. Hub location and allocation optimization ofmultiple allocation hub-and-spoke express networks[J].SystemsEngineering-Theory&Practice, 2012, 32(2):441-448.
[20] CAMPBELL J F. Integer programming formulations of discrete hub location problems[J].EuropeanJournalofOperationalResearch,1994,72(2):387-405.
[21] CAMPBELL J F. Hub Location and the p-hub median problem[J].OperationsResearch,1996,44(6):1-13.
[22] ERNST A T, KRISHNAMOORTHY M. An exact solution approach based on shortest-paths for p-hub median problems[J].InformsJournalonComputing,1998,10(2):149-162 .
[23] O'KELLY M E, BRYAN D. Hub network design with single and multiple allocation: A computational study[J].LocationScience,1996,4(3):125-138.
[24] SKORIN-KAPOV D,SKORIN-KAPOV J,O'KELLY M. Tight linear programming relaxations of uncapacitated p-hub median problems[J].EuropeanJournalofOperationalResearch,1996,94(3):582-593.
[25] CONTRERAS I, DAZ J A, FERNNDEZ E. Lagrangean relaxation for the capacitated hub location problem with single assignment[J].ORSpectrum,2009,31(3):483-505.
[26] CORREIA I, NICKEL S,SALDANHA-DA-GAMA F. Hub and spoke network design with single-assignment, capacity decisions and balancing requirements[J].AppliedMathematicalModelling, 2011, 35(10): 4841-4851.
[27] 胡青蜜, 胡志华, 陶莎. 二级轴辐式零担物流网络设计的资源均衡利用问题[J].公路交通科技, 2013, 30(4): 124-131. HU Qingmi, HU Zhihua, TAO Sha. Resource balanced usage problem for bi-level hub-and-spoke LTL logistics network design[J].JournalofHighwayandTransportationResearchandDevelopment, 2013, 30(4):124-131.
[28] ALUMUR S A, NICKEL S,SALDANHA-DA-GAMA F. Hub location under uncertainty[J].TransportationResearchPartB:Methodological,2012,46(4):529-543.
[29] CONTRERAS I, JEAN-FRANGOIS, LAPORTE G. Stochastic uncapacitated hub location[J].EuropeanJournalofOperationalResearch,2011,212(3):518-528.
Contradistinction between Spoke Allocation Models in Hub-Spoke Network with Multistage Capacitated
YANG Bin, YIN Yuqi, HU Zhihua
(Logistics Research Center, Shanghai Maritime University, Shanghai 201306, P.R.China)
In order to find the practical differences between single allocation and multi-allocation of spokes in hub-spoke network (HSN), the problem of the contradistinction between spokes’ allocation patterns in HSN under multi-stage capacitated was proposed, and the characteristics of two allocation patterns with uncertain demand were studied. Based on the basic model of HSN design, the mixed integer programming models of two kinds of distribution modes were established, which took the operating costs of HSN with multistage capacitated into consideration. According to the predicted demand scenes and their probability distribution, the optimal expected costs of the two network models were solved to design the hub and spoke network. Through setting three HSN design experiments, that is the optimal network design, the pre-specified number of hubs to locate and the changes in total demand, the network cost, the hub configuration and utilization rate of single allocation and multi-allocation models of spokes in the above experiments were contrasted. It is discovered that the multi-allocation network has the advantages of lower network cost, less number of hubs and higher utilization rate of the hub.
traffic and transportation engineering; single allocation; multi-allocation; hub-spoke network; multistage capacitated; demand uncertainty
10.3969/j.issn.1674-0696.2016.03.30
2014-11-20;
2015-05-06
国家自然科学基金面向项目(71471109);交通运输部科技项目(2015328810160);上海市科委科研计划项目(14DZ2280200, 14511107402);上海市教委科研创新项目(14YZ100);上海市曙光计划项目(13SG48);上海海事大学研究生创新基金项目(2014ycx013)
杨 斌(1975—),男,山东招远人,教授,博士,主要从事绿色物流、知识发现与智能系统方面的研究。E-mail:binyang@shmtu.edu.cn。
尹宇起(1991—),男,山东莱阳人,硕士研究生,主要从事绿色物流方面的研究。E-mail:yyq5403@163.com。
U49
A
1674-0696(2016)03-147-08
