基于原位试验的桥梁施工过程应力修正
2016-05-22向中富
向中富,冉 旭,赖 溧
(重庆交通大学 土木工程学院,重庆 400047)
基于原位试验的桥梁施工过程应力修正
向中富,冉 旭,赖 溧
(重庆交通大学 土木工程学院,重庆 400047)
针对混凝土桥梁施工过程结构真实应力识别需要,通过现场测试与原位试验,埋设无应力传感器试件,对弦振式传感器测量的混凝土应变增量中的温度与收缩徐变影响进行有效修正,研究有效扣除温度自由应变,混凝土收缩徐变的方法,找出应变增量与混凝土应力应变的关系,形成混凝土桥梁施工过程结构真实应力监测实用方法,指导弦振式传感器现场测量应力修正。
桥梁工程;混凝土;应力;温度;收缩徐变;修正
0 引 言
目前,在混凝土桥梁监控中通常采用埋置弦振式传感器进行混凝土应力监控。弦振式传感器可以较为精确地测量出混凝土的真实应变ε测=ε真。但由此准确推算出混凝土的真实应力比较困难,这是因为混凝土应变包含因结构自重、外荷载作用下的弹性变形εe、温度变形εt、混凝土收缩变形εξ、混凝土徐变变形εφ等。简单地从测量出来的总应变中扣除温度收缩徐变换算得到的应力往往与真实应力相差甚远。混凝土桥梁大多是超静定结构,因而会由于变形协调而产生约束应力,即未发生应变而产生应力,如温度与收缩应变中受到约束的那一部分。
关于混凝土弦振式应变计应力监控与计算的研究已较多,弦振式应变的测量计原理及各种标定方法研究也已深入,弦振式应变已经大规模地生产应用。美国基康公司专门针对弦振式应变计编制了一本标定K值的计算书与使用说明书;李滨等[1]总结了弦振式应变计K值各种标定方法,如加权平均法、最小二乘法、回归衰减法。王国杰等[2]针对混凝土结构早龄期应力相关应变现场监测与分析,对混凝土凝结硬化过程中应变的产生、发展和变化过程进行了分析。江湧等[3]针对桥梁施工提出混凝土实测徐变应变的计算方法但并不全面;李静等[4]针对广州广清卫生河大桥施工监控中的应力监测得出了一套比较系统的徐变应变分离方法。韩大建等[5]研究了大跨度混凝土斜拉桥主梁应力监控中的徐变应变分离。关于PC混凝土梁桥温度修正国内也有多人研究,程慧林[6]研究了灵江特大桥连续梁施工应力监控中消除温度影响的方法。郭超[7]研究了混凝土结构温度应力特性及测定方法,对混凝土温度应力的测试方法进行了非常详细的分析,初步研究了在不同约束情况下混凝土的温度应力计算方法。
对于悬臂施工的连续刚构桥或连续梁桥,在合拢前为一端固结一端自由的悬臂梁,即为静定结构,因而,只需修正混凝土应变中非受力引起的应变部分,包括温度变化、收缩徐变等,最后通过ε0×E0即可得出混凝土中的真实应力。
曾德荣[8]提出了桥梁施工监测应力误差计算方法,提出测量应力增量来减少误差的方法,其中对于温度,收缩徐变都只采用理论公式进行修正,并未对理论公式修正方法的可行性与有效性做出研究。笔者在其研究的基础上,针对每个修正项,通过现场原位实验,对比理论公式修正与其他方法修正的正确性,提出了一套满足工程精度要求的可行的修正应变增量法。
1 温度应变修正
理论上:
ε测=k(f2-f20)
(1)

可以认为,当温度升高ΔT时,弦振式应变计内部的钢弦伸长α钢·ΔT,其中α钢=1.2×10-5,基本为定值,因为L≫α混·ΔT,故可以认为k为一个定值。
温度升高ΔT时,混凝土构件伸长α混·ΔT,从而可推得理论修正公式:
ε测=(α混-α钢)ΔT=k(f2-f02)
(2)
实际中测量的数据却与理论存在较大误差,下面通过实验来验证理论公式修正的可行性。
用理论修正的温度产生的自由膨胀与用应变计实际测量的应变如表1[7]。

表1 温度变化时实际测量的应变值

在混凝土温涨系数未知情况下,测量混凝土温度应变,运用钢弦的线膨胀系数为定值,弦振式传感器所测应变包含混凝土温涨变形。把ε测=(α混-α钢)ΔT=k(f2-f02)变为ε混=α钢·ΔT+ε测。
通过实验得出的结构混凝土实际变形与采用试块修正变形与按理论计算的变形如表2[7]。
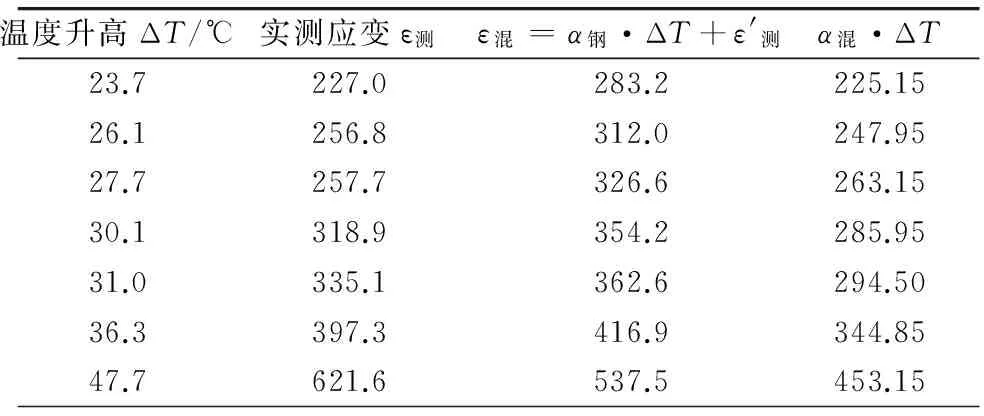
表2 温度变化时实际测量与理论计算的应变值
由表2可知,误差在可接受范围以内,因此,在实际监测中,不宜采用(α混-α钢)ΔT来修正静定结构的温度应变,可采用现场制作试块的方法进行修正。
2 混凝土收缩修正
影响混凝土收缩的因素非常多,包括:水泥的品种,混凝土配合比,骨料品种及含量,外加剂种类和掺量,周围介质条件,养护条件,混凝土龄期,自身结构和碳化作用等。很难通过某一理论或经验公式考虑如此多的因素,《规范》考虑混凝土的收缩参数有:混凝土的龄期,混凝土强度等级,年平均相对湿度,水泥的品种,结构的理论厚度。
目前,考虑较全面的经验公式是美国ACI建议的方法,是以最终的收缩值来估算混凝土前期的收缩值:
(3)
εs,∞与养护时间,环境湿度,构件尺寸,混凝土配合比,骨料含量,水泥用量,混凝土含气量有关。
为对比规范公式计算修正的收缩值与应变计测量的收缩值,现采用现场制作C55混凝土试块实测与规范计算进行对比,如图1。

图1 理论计算收缩与实际测量收缩对比Fig.1 Shrinkage contrast between theoretic calculation and actual measurement
由图1可见,理论公式计算值大于应变计测量值。在桥梁受力计算时,理论公式计算的收缩值是偏安全估计,但是在监控中,采用理论公式修正时,从总应变中过多扣除收缩应变,使得最后得到的应力应变值变小,导致最后监控算得的应力值变小,结果偏不安全。实际监控中,建议采用现场制作试块的方法修正收缩应变。
3 混凝土徐变修正
3.1 徐变计算方法
对于混凝土徐变量的计算,目前主要是依据各种规范对混凝土徐变系数的计算进行估算。较为精确的方法需针对现场混凝土预制试块预压进行测定徐变系数,计算徐变变形。
3.2 徐变理论分析
混凝土徐变受很多因素影响,外部因素包括加载龄期,加载应力,持荷时间,相对湿度,试件尺寸,混凝土碳化;内部因素则有水泥,骨料,水灰比,外加剂,粉煤灰等。目前,计算混凝土徐变使用较多的是考虑参数最多的朱伯芳院士提出的10参数模型方程[9]:
c(t,τ)=(f1+g1τ-p1)[1-e-γ1(t-τ)]+(f2+g2τ-p2)[1-e-γ2(t-τ)]+D(e-γ3τ-e-γ3t)
由于参数多,采用最小二乘法或回归分析方法较难确定参数,根据现场测量数据采用试算方法分析的公式实用性不强。朱伯芳院士在此基础上提出了6参数方法,《规范》针对6参数方法做了进一步简化。
无论是哪一种计算方法,计算误差都在20%~ 40%以内。实践表明,针对现场试件测得的徐变系数能比较精确地修正弦振式传感器应变读数,但较为麻烦,在工程上的可行性低。
由于混凝土梁桥结构混凝土受力通常不会超过0.4倍的自身承载能力极限值,此时混凝土徐变一般处于线性变化范围,徐变变形与应力大小成正比,符合鲍尔茨曼(L.BOLTZMAN)叠加原理,即在时间t内,总应变ε(t)为每一次应力增加Δσn(τn)引起的应变的总和:
(4)
式中:τ0为第一次加荷龄期;J(ti,τi)为徐变函数。
由此引出了很多种徐变计算的理论方法,如有效弹模法,老化理论法,弹性徐变理论(叠加法),弹性老化理论(流动率法)和继效流动理论法。每种方法都针对不同的受力情况。对于应力在剧烈变化,且应力一直在增大的情况下宜采用弹性徐变理论叠加法计算。叠加法由前苏联教授马斯洛夫创立,理论假定变形和应力之间成线性关系,应力变化引起的徐变总变形可以按每段应力增量引起的徐变变形的总和来计算。
4 测量应变与真实应变的关系推导
以悬臂施工混凝土梁式桥为例,不同阶段的结构应力状态不同,一是挂篮和模板的前移过程,二是混凝土浇筑过程,三是钢绞线张拉的过程。上述3个阶段经历时间都较长,即便挂篮前移都需要6 h以上,混凝土浇筑和钢绞线张拉可能需要12 h以上,而这期间发生的徐变会占到其最终徐变总量的10%~20%左右。所以,这个阶段的结构应变不能视为弹性变形,必须要加上混凝土的徐变变形计算。实际工程中的结构应力变化非常复杂,为了简化计算,这里提出一种理论计算假定,假定应力在这些阶段的变化为线性增加或减少。
现通过原位试验来分析测量应变与真实应变之间的关系。在现场箱梁内8个位置埋设弦振式传感器,如图2,其中在顶板和底板埋设两个无应力传感器。无应力传感器如图3,传感器必须捆绑在其纵向受力钢筋上,保持顺直,在混凝土浇筑28 d后开始进行测量。测量挂篮推前后,混凝土浇筑前后,预应力张拉前后的应变数据。并记录每个工况持续时间。

图2 箱梁传感器布置示意Fig.2 Schematic diagram of box beam sensor arrangement

图3 无应力传感器埋设示意Fig.3 No stress sensors embedment
考虑到计算误差与修正误差的累积,在进行实测数据与理论数据对比时,采用应力增量去对比,而不是采用应力总量进行对比,即对比混凝土浇筑前后应力的增量与理论计算的混凝土应力的增量。测量阶段有混凝土挂篮模板移动前后,混凝土浇筑前后,张拉预应力前后。测量数据计算分析如下。
根据传感器标定的k值可以计算出混凝土各阶段的实际应变:
εn=k(fn2-f2n-1)
(5)
式中:εn为传感器直接测量出的应变。
根据埋设的自由试件的无应力传感器(图3)只有一个面与混凝土箱接触,其余5个面用泡沫板隔开使其不参与受力。测量自由试件计算出混凝土温度与收缩的应变:
εn0=k0(f2n0-f2n-1)
(6)
式中:εn0为自由试件的温度变形与收缩变形之和。
从所测实际应变中扣除温度变形与收缩变形的影响后可得到本阶段的应变增量:
Δεn=εn-εn0
(7)
式中:Δεn为测量工况前后有关应力的应变增量,包含弹性应变与徐变。
又根据徐变叠加理论可以得出

(8)
式中:等号右边第1项为当前施工阶段应力变化导致的应力应变增量;第2项为此施工阶段完成时刻t前所有应力在当前施工阶段结束后引起的应力应变增量;第3项为此施工阶段前所有应力在此施工阶段前引起的应力应变增量。
徐变系数φ(t,τ)=E(τ)c(t,τ)。
采用《规范》计算混凝土徐变系数:
φ(t,τn)=E(τn)c(t,τn)=φ0·βc(t-τn)
(9)
(10)
式中:φ0=φRH·β(fcm)·β(τn)〔φRH只和湿度与构件理论厚有关;β(fcm)只与混凝土强度有关;β(τn)只与混凝土加载时的龄期有关〕;βH只与湿度与构件理论厚度有关。这些量都与加载龄期无关,为不变量。
令
(11)
式中:Δεi为i阶段前所有其他应力产生的徐变变形。
本阶段的应力增量导致的应变增长量为:
Δεm=Δεn-Δεi
代入《规范》相应公式,并假定这些阶段应力变化为线性增加或减少,则
(12)
当混凝土龄期达到28 d以后认为混凝土弹性模量不随时间变化而改变,则带入《规范》公式得
(13)
其中积分公式难以用常用积分公式计算,现采用MATLAB软件求出一个数值解,最终可以求得应力增量。式(13)即为测量应变增量与真实应力增量的关系。
5 工程应用
5.1 工程简介
重庆酉阳至贵州沿河高速公路某大桥为预应力混凝土连续刚构桥,跨径布置为(98+180+98) m。采用挂篮分阶段悬臂浇筑施工,采用埋置式弦振式传感器进行应力监测,弦振式传感器埋设于0 # 块端部。
5.2 现场传感器量测结果
监测中实测数据较多,现针对8#块预应力张拉阶段进行分析。8 # 块预应力张拉阶段在仪器埋入后第94 d进行施工,张拉持续时间为11 h。对张拉前后阶段进行量测,结果见表3。

表3 现场测量应变
因直接由测量计算出来的应变并不是应力应变,对测量出来的应变εn进行修正,代入式(5)~式(13)计算出张拉后的应力增量,见表4。

表4 修正应变应力计算结果
各测点经过修正后,误差分别减少14.2 %,16.8 %,13.1 %,修正应力增量法能有效减少误差。
5.3 应力修正及结构真实应力识别
采用式(13)修正应力增量法,对1#块~13#块每个施工阶段前后测量并计算修正,且与有限元软件的计算结果对比,结果如图4。



图4 应力增量Fig.4 Stress increment
由箱梁顶板的修正所得应力结果与理论计算结果对比可以明显看到箱梁存在明显的剪力滞效应。顶板中间的应力明显小于腹板的应力,理论公式考虑的徐变量比实际的徐变量大,导致考虑的弹性应变量小,故测量出来的应力增量都略小于理论增量。
一般PC混凝土连续梁桥采用挂篮施工,其箱梁底板上的应力变化是正负交替的。虽然通过设置无应力计可以很好地修正收缩与温度带来的形变影响,但是对徐变带来的影响只能用理论估算。而且徐变叠加法认为卸载后的徐变恢复曲线和加载徐变曲线完全相同,即认为徐变是可以完全恢复的与实际情况存在出入。故对于箱梁底板这种应力变化范围很小且正负变化时,此种修正方法精度无法达到要求。
6 结 论
1)在实际条件下,混凝土结构通常处在温度场、湿度场、应力场随时发生变化的环境,导致非应力应变与应力应变随时发生变化,有效测量混凝土真实应力应变变得困难。通过现场原位实验与室内实验对比并埋设非应力应变即时补偿试件,从总应变中分离非应力应变,能有效地减少测量误差、计算误差及环境误差的累积。
2)采用弦振式传感器现场测量的混凝土应变包含有温度与收缩徐变影响,需要进行修正。笔者通过现场原位实验讨论温度与收缩徐变修正的理论与实践方法在修正应中的可行性,精度是否满足要求,实用性能否推广的前提下,建立了在混凝土桥梁施工过程中结构真实应力监测实用方法,即修正应力增量法。工程应用结果表明,修正应力增量法能有效识别现场量测应力中的非力学应力部分,对混凝土桥梁施工过程结构应力监测的可靠性保证具有重要意义。
[1] 李滨,钟文斌,林飞振.弦振式应变计数学模型比较分析[J].上海计量测试,2013(4):8-11. LI Bin,ZHONG Wenbin,LIN Feizhen.String vibration type strain gauge mathematical model for comparative analysis[J].ShanghaiMeasurementandTesting,2013(4):8-11.
[2] 王国杰,郑建岚.混凝土结构早龄期应力相关应变现场监测与分析[J].工程力学,2009,26(9):61-73. WANG Guojie,ZHENG Jianlan,In site monitoring and analysis for stress-dependent strains of early age concrete structures[J].EngineeringMechanics,2009,26(9):61-73.
[3] 江湧,荆秀芬,石雪飞.桥梁施工监控测试中混凝土实测徐变应变的计算方法[J].桥梁建设,2005(增刊1):145-147. JIANG Yong,JING Xiufen,SHI Xuefei.Calculation method for concrete creep strain measured in field in bridge construction monitoring[J].BridgeConstruction,2005(Sup1):145-147.
[4] 李静,殷建军,王卫锋,等.广州广清卫生河大桥施工监控中的应力监测[J].重庆建筑大学学报,2006,28(4):68-71. LI Jing,YIN Jianjun,WANG Weifeng, et al.Stress measuring during the construction monitoring of Weisheng River Bridge in Guangzhou[J].JournalofChongqingJianzhuUniversity, 2006, 28(4): 68-71.
[5] 韩大建,徐郁峰,王卫锋,等.大跨度混凝土斜拉桥主梁应力监控中徐变应变的分离[J].桥梁建设,2003(1):766-771. HAN Dajian, XU Yufeng, WANG Weifeng, et al. Separation of creep strain in stress monitoring for main girder of long-span concrete cable-stayed bridge[J].BridgeConstruction,2003(1):766-771.
[6] 程慧林.灵江特大桥连续梁施工应力监控中消除温度影响的方法[J].铁道标准设计,2009(8):44-47. CHENG Huilin. Method for eimination of temperature lnfluence in monitoring stress in construction of Lingjiang Super Large Bridge[J].RailwayStandardDesign,2009(8):44-47.
[7] 郭超.混凝土温度应力的实验测定[D].天津:天津大学,2011. GUO Chao.ExperimentalDeterminationofConcreteThermalStress[D]. Tianjin: Tianjin University,2011.
[8] 曾德荣.桥梁施工监测应力误差计算方法[J].公路交通技术,2005,8(4):113-116.
ZENG Derong. Method for stress error calculation during bridge construction monitoring[J].TechnologyofHighwayandTransport, 2005,8(4):113-116.
[9] 朱伯芳.混凝土的弹性模数、徐变度与应力松弛系数[J].水利水电,1985(9):161-171. ZHU Bofang. Modulus of elasticity, specific creep and coefficient of stress relaxation of concrete[J].WaterResourcesandHydropower, 1985(9):161-171.
Stress Modification of Bridge Construction Based on the In-situ Experiment of Bridge
XIANG Zhongfu, RAN Xu, LAI Li
(School of Civil Engineering, Chongqing Jiaotong University, Chongqing 400074, P.R.China)
In view of the identification demand of structure real stress in the process of concrete bridge construction, no-stress sensor components were embedded in the bridge through the field test and in-situ test. And the temperature and shrinkage creep effects in concrete strain increments measured by string vibration sensor were modified effectively. A method to take off the temperature free strain and shrinkage creep of concrete was researched. Finally, the relationship between strain increments and concrete stress-strain was found out to develop a practical method to monitor the real stress in construction process of concrete bridge and to guide the modification of the stress measured by string vibration sensor.
bridge engineering; concrete; stress; temperature; shrinkage creep; correction
10.3969/j.issn.1674-0696.2016.03.02
2015-07-15;
2015-10-22
向中富(1960—),男,四川苍溪人,教授,博士生导师,主要从事桥梁技术理论与施工技术方面的研究。E-mail:xzf6058@126.com。
U445
A
1674-0696(2016)03-006-05
