改进的EEMD去噪方法及其在谐波检测中的应用研究

孙曙光, 庞 毅， 王景芹， 张 超， 杜太行

(1. 河北工业大学控制科学与工程学院， 天津 300130； 2. 河北工业大学电气工程学院， 天津 300130； 3. 陕西科技大学电气与信息工程学院， 陕西 西安 710021)

改进的EEMD去噪方法及其在谐波检测中的应用研究

孙曙光1, 庞 毅1， 王景芹2， 张 超3， 杜太行1

(1. 河北工业大学控制科学与工程学院， 天津 300130； 2. 河北工业大学电气工程学院， 天津 300130； 3. 陕西科技大学电气与信息工程学院， 陕西 西安 710021)

针对低信噪比条件下集合经验模态分解(EEMD)在分解过程中产生的模态混叠问题，本文提出改进的 EEMD阈值去噪方法。首先利用白噪声经EEMD分解后其固有模态函数(IMF)分量中能量密度与平均周期乘积为常量的特性确定有用信号与含噪信号的分界点，对含噪信号进行“粗筛”；进而对粗筛出的含噪模态进行“细筛”，在此过程中采用“3σ法则”对第一层噪声信号进行细节处理，从而更好地保留有用信号的细节特征，继而通过能量估算方式对其他各个含噪模态进行阈值处理；最后进行信号重构。选取信噪比与均方误差作为去噪效果评价标准，经与实验对比分析，结果表明本文方法达到了最佳的去噪效果，尤其在低信噪比时优势更加明显。基于以上去噪方法，本文又进一步提出了基于二次EEMD分解的谐波检测方法，结果表明该方法可实现在低信噪比下的谐波检测，进一步证明了所提去噪方法的有效性。

EEMD； 阈值去噪； “3σ法则”； 二次EEMD分解； 谐波检测

1 引言

集合经验模态分解(Ensemble Empirical Mode Decomposition，EEMD)完全自适应将复合信号分解成不同时间尺度的固有模态函数(Intrinsic Mode Function，IMF)，不需要人为选择基函数和分解层数，利用其分解结果可以准确有效地把握原数据的特征信息[1-4]。但在工业现场中，因环境恶劣，采集到的信号往往含大量的噪声，而EEMD方法在低信噪比情况下，对信号的分解会产生模态混叠问题，从而对提取信号中的特征量造成了很大的影响[5]。

目前针对非平稳信号的降噪方法有小波阈值去噪方法[6-9]和基于EEMD分解的去噪方法[10-15]等。文献[6,7]中改进的小波阈值去噪采用软硬阈值相结合的方法，改善了软阈值和硬阈值的固有弊病，虽然去噪效果很好，但对小波基和分解层数的选取具有很大的依赖性。文献[10,11]中直接阈值去噪法是以EEMD分离出的第一层模态作为噪声信号，然后对各层噪声能量进行估算，进而对其进行阈值去噪处理，如此会对后几层未含噪声模态中的有用信号有所滤除。文献[15]中的部分重构去噪法是先确定噪声模态，然后对其直接滤除，但滤除的模态中可能含有有用信号。因此，如何判断噪声分量和有用分量的分界点并且提取噪声分量中的有用信号成为影响去噪效果的关键[14]。

针对上述问题，结合不同算法间的优势，本文提出了改进的EEMD阈值去噪方法。该方法利用白噪声分解的各层IMF分量中能量密度与平均周期乘积为常量的特性，对含噪信号进行“粗筛”，筛选出含噪模态，从而克服EEMD直接阈值去噪的不足；然后利用“3σ法则”[16]与阈值处理相结合方式对含噪模态进行“细筛”，克服了EEMD部分重构去噪的不足。该方法在达到去噪效果的基础上，更好地保护了原始信号的细节信息不被破坏，保持了其原始特性。

同时本文在改进EEMD阈值去噪的基础上，提出了基于二次EEMD分解的谐波检测方法[17,18]。以信噪比、均方误差及相关度作为相应的评判标准[19,20]，经仿真分析，验证了本文去噪及谐波检测方法的可行性与有效性。

2 EEMD基本原理

针对EMD存在的模态混叠问题，EEMD通过在分解过程中叠加高斯白噪声，削弱了模态混叠的现象。EEMD是以EMD算法为核心进行的改进，所以EEMD和EMD的主要算法结构大体相同。大致步骤如下。

(1) 将高斯白噪声ω(t)加入目标信号X(t)得到一个总体信号；

X′(t)=X(t)+ω(t)

(1)

式中，X′(t)为加入白噪声后的信号。

(2)将X′(t)进行EMD分解，得到各阶IMF分量：

(2)

式中，rn(t)为分解后的剩余分量。

(3)重复步骤(1)和步骤(2)，但是每次加入的高斯白噪声ωi(t)是不同的，即

(3)

(4)利用高斯白噪声频谱的零均值原理，消除高斯白噪声作为时域分布参考结构带来的影响，分解后相应的IMF分量的整体平均值就是最终的结果，cn(t)可表示为：

(4)

EEMD中高斯白噪声的加入服从式(5)：

(5)

式中,ε为高斯白噪声的幅值;N为加入高斯白噪声的总体个数；εn表示原始信号与各阶的IMF相加后之间的误差。根据文献[20]，N取100～300时，残留的白噪声误差已处于较低水平，同时ε选择0.01～0.5倍信号标准偏差较为适宜。此外，ε和N可随信号的强度适当增大。针对本文的研究对象，ε选择0.2,N为300。

3 改进的EEMD阈值去噪方法

3.1 含噪信号的“粗筛”处理

根据EEMD的分解原理，将信号分解成频率由高到低的一系列IMF分量，而在实际中噪声往往为高频分量。在EEMD分解中，各层IMF中所含的噪声分量不同，且逐级递减，甚至后几层存在不含噪声的模态，若对所有模态进行阈值去噪就会筛掉一部分有用信号，因此本文利用高斯白噪声分解后各层IMF分量中能量密度与平均周期乘积为常量的特性，自动确定信号中含噪模态，进行“粗筛”处理。具体步骤如下[5,15]。

(1)对含噪信号进行EEMD分解后，得到M条IMF分量，根据式(6)和式(7)分别计算各层IMF的能量密度和平均周期：

(6)

(7)

式中,n为每个IMF的长度;Oi为第i条IMF分量的极值点总数。

(2)根据式(8)计算出各层IMF分量的能量密度与平均周期之积：

(8)

(3)通过式(9)计算筛选条件：

(9)

当RPi≥2时，可知第i条IMF的Pi相对于前i-1条IMF的Pi-1的平均成倍增大，令K=i-1，可确定前面K条IMF分量为主要含噪模态，并对其进行“细筛”处理。

3.2 含噪模态的“细筛”处理

此部分主要是精确确定每层含噪模态的阈值，并进行阈值处理，提取有用信号。

常规EEMD去噪算法通常认为第一层IMF全部由噪声构成[10,11]，但经研究发现IMF1中仍含有一定量的信号细节信息[16]。在IMF1中噪声占绝大部分，且高斯噪声近似服从零均值正态分布，所以非常适合采用“3σ法则”进行细节信息提取，可表示为：

(10)

(1) 根据式(11)，对IMF1中噪声能量进行计算：

(11)

(2)以IMF1的能量作为参考，由于分解后的能量逐层衰减，所以根据式(12)对其余各层的能量进行估算：

(12)

式中，参数β≈0.719，ρ≈2.01(学者Flandrin研究给出)；K为含噪声的层数。通过式(12)估算出其余IMF所含噪声的能量。

(3)根据式(13)，对各层所含噪声的标准差进行估计：

(13)

(4)根据式(14)，计算出第二层阈值系数C2作为相应的参考标准，然后根据式(15)计算其余各层的阈值系数。对于给定信号经EEMD分解后，通常前几层所含噪声的比重比较大，之后的几层中有用信号占其成分的绝大部分，因此各层IMF阈值系数的选取应得当，以免将有用成分误当作噪声而滤除。根据本文所给信号的模型，噪声分量相对较大，所以阈值系数相应增大[11]，经实验分析，选用后一层阈值系数为前一层的3/4，达到更好的去噪效果。

(14)

(15)

(5)根据式(16)计算各层的阈值：

(16)

(6)根据文献[6]中提及的软阈值和硬阈值处理的缺点，本文采用软硬阈值的方式进行去噪处理，公式如下：

(17)

最后将含噪信号“粗筛”筛选出的未含噪模态与含噪模态“细筛”后的有用信号进行信号重构。本文改进的EEMD阈值去噪方法整体步骤如图1所示。

图1 本文去噪方法步骤Fig.1 Denoising steps of this paper

4 改进EEMD去噪方法的实验分析

本文选择了一种日常生活中电网实际负载电流模型，表达式如下：

x(t)=100sin(100πt)+40sin(300πt)+

30sin(500πt)+20sin(700πt)+10sin(1100πt)

(18)

该模型信号含有5种成分，第一项代表的是工频50Hz的基波信号，其余四项分别为3、5、7和11次谐波信号，幅值大小分别为40A、30A、20A和10A，采样频率设置为12800Hz。为了分析改进EEMD阈值去噪的效果，本文选择对给定的电流模型叠加信噪比为15dB高斯白噪声作为实验对象。模型波形如图2所示，其中上曲线为该模型的波形图，下曲线为添加高斯白噪声的波形。

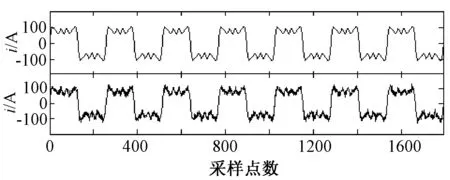
图2 加噪声的信号Fig.2 Signal with noise

为验证本文改进的阈值去噪方法的优势，与文献[6]中改进小波阈值去噪方法、文献[10]中EEMD直接阈值去噪方法以及文献[15]中EEMD部分重构去噪方法进行比较分析。图3为以上四种方法对于图2加噪信号去噪的效果，其中上曲线为去噪后信号，下曲线为去噪后信号与原始信号的差值。

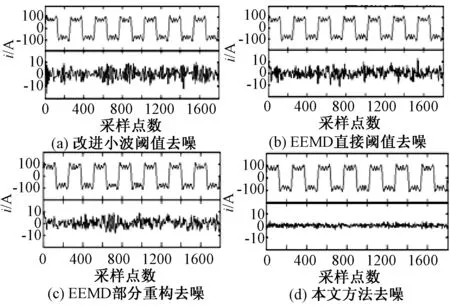
图3 不同方法的去噪效果Fig.3 Denoising effect for different methods

从图3可以看出，本文去噪方法去噪后信号与原始信号差值最小，去噪效果最好。此外，对四种方法在不同信噪比下的去噪效果进行对比，以信噪比(SNR)和均方误差(RMSE)作为评判标准。根据文献[19]以及式(19)和式(20)可知，去噪后信噪比越大，均方误差越小，说明去噪效果更好。

(19)

(20)

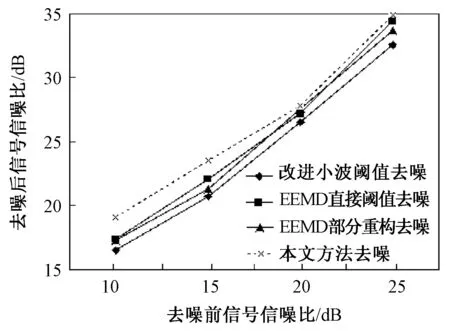
图4 不同方法对信号去噪后的信噪比比较Fig.4 Comparison of SNR after denoising for different methods

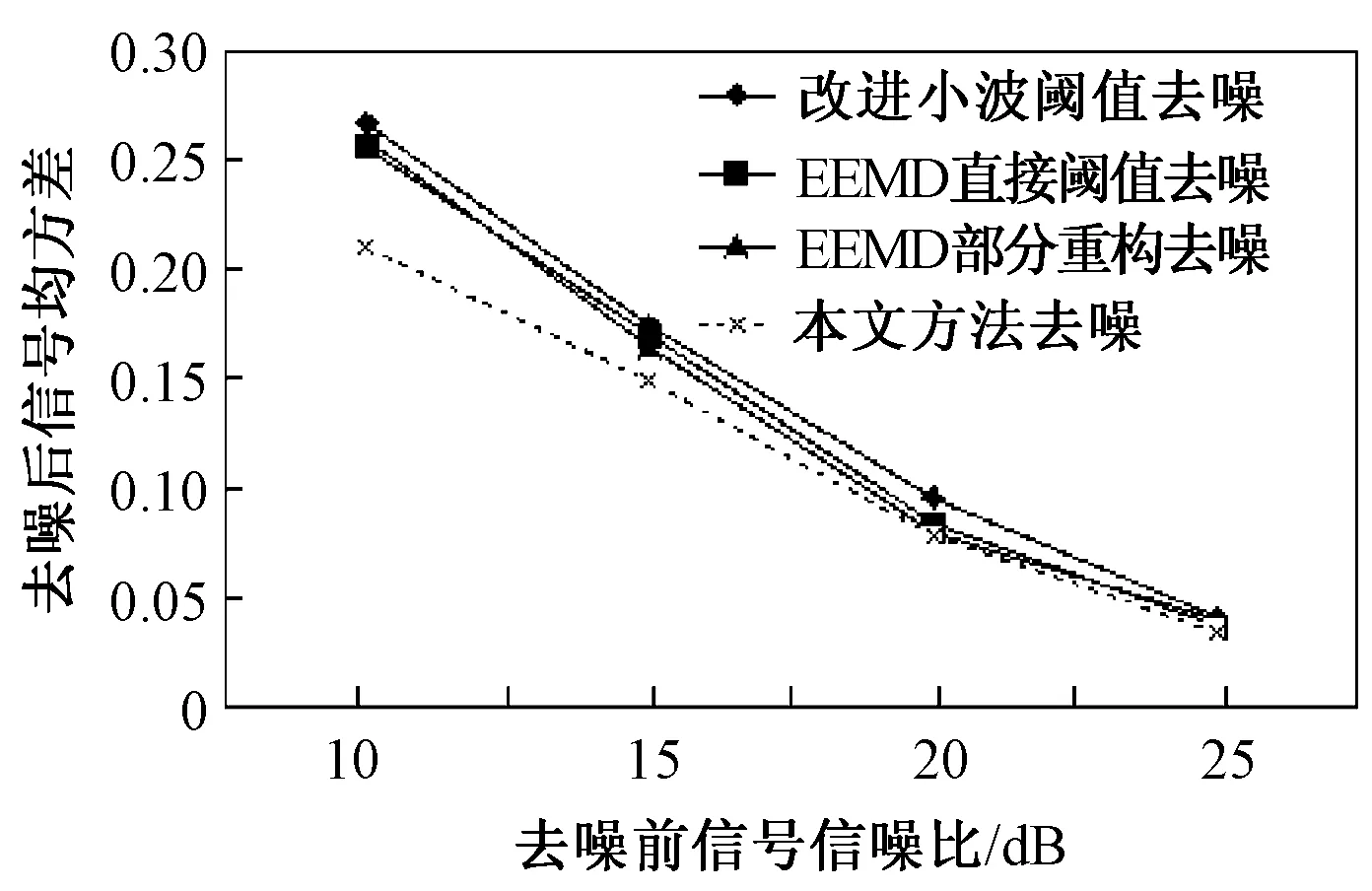
图5 不同方法对信号去噪后的均方误差比较Fig.5 Comparison of mean square error after denoising for different methods

可以明显看出，本文方法在各种情况下去噪后的SNR和RMSE均优于其它方法，而且当信噪比较低时，本文方法的优势更加明显。图6为去噪后信号与原始不含噪信号的对比图，其中虚线为原始信号，实线为去噪后信号。

图6 去噪效果Fig.6 Effect after denoising

可以看出，去噪后信号明显大幅度消除了噪声的毛刺现象，且与原始信号近乎重合，很好地保留了原始信号的固有特性。

5 基于二次EEMD分解的谐波检测实验分析

在低信噪比条件下，直接利用EEMD分解很难有效地分解出各个IMF。图7为直接利用EEMD对图2中15dB信噪比信号的分解效果，自上至下分别为11、7、5、3次谐波和基波信号波形。可以明显看出，各次谐波间发生了严重的模态混叠现象。

图7 EEMD对含噪信号分解效果Fig.7 EEMD decomposing result for harmonic signal with noise

对于谐波检测而言不仅需要有效地去除噪声，同时还要保留信号的原始特性。结合改进的EEMD阈值去噪方法，本文提出的基于二次EEMD分解的谐波检测方法如图8所示。

图8 二次EEMD分解过程Fig.8 Decomposition processing of two EEMD

图9至图12分别为利用图3中的其他3种方法对信号去噪后再进行EEMD分解以及本文谐波检测方法的检测结果。图12对检测结果与标准模型信号进行了对比，实线为检测结果，虚线为标准模型信号。

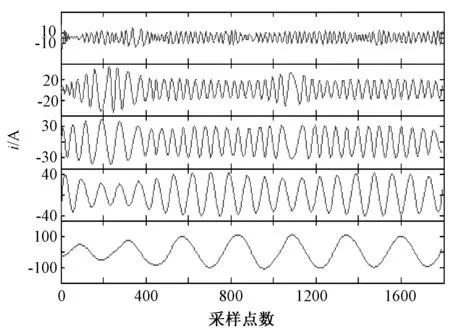
图9 改进小波阈值去噪后分解的谐波检测结果Fig.9 Harmonic detection effect of decomposition after improved wavelet threshold denoising

图10 EEMD直接阈值去噪分解的谐波检测结果Fig.10 Harmonic detection effect of decomposition after EEMD direct threshold denoising

图11 EEMD部分重构去噪分解的谐波检测结果 Fig.11 Harmonic detection effect of decomposition after EEMD partial reconstruction denoising

图12 本文方法谐波检测结果Fig.12 Harmonic detection effect in this method

可以看出，在15dB低信噪比条件下，其他三种方法检测结果的模态混叠问题比较严重。由图12可以看出，本文方法检测结果各模态中间部分与原始信号吻合度很高，可用于谐波检测。图13为本文方法在20dB信噪比下的谐波检测结果，其中实线为检测结果，虚线为标准模型信号。可见随着原始

信号信噪比的增加，检测精度可以得到进一步提升，忽略端点问题，各次谐波检测结果与电流模型的各分量吻合，通过Matlab中的corrcoef函数，计算二者相关度，均达到99.81%以上。

图13 20dB含噪信号的谐波检测结果Fig.13 Harmonic detection effect for signal under 20dB SNR

6 本文方法在晶闸管整流电路谐波检测中的应用

采用Matlab搭建仿真模型，谐波源采用一个带阻感性负载的三相桥式晶闸管整流电路，工频50Hz，采样频率12800Hz，其中以A相负载侧电流波形为例，同时叠加20dB高斯白噪声，如图14所示。

图14 A相负载侧电流波形Fig.14 Load side current waveform of phase A

为验证本文方法的检测效果，与EEMD方法直接检测的效果进行比较。总谐波电流信号为原始信号减去检测出的基波电流信号。图15和图16分别为EEMD、本文方法对图14含噪电流谐波信号的检测效果，其中上图实线表示原始信号，虚线表示检测出的基波电流信号，下图表示检测出的总谐波电流信号。

图15 EEMD检测效果Fig.15 Detection result of EEMD

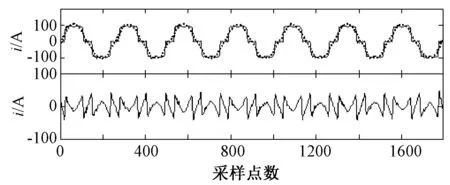
图16 本文方法检测结果Fig.16 Detection result of this method

通过与原始信号幅值的对比发现，由于存在噪声干扰，造成了EEMD分解出的基波成分少部分丢失；由于基波电流检测不准，所以谐波电流信号中叠加有基波信号。

由图16可知，本文方法能够很好地消除噪声的干扰，同时保留了信号的原始特征，有利于精确检测出基波电流信号；从总谐波电流信号可以看出，其中不存在基波电流成分。

7 结论

本文提出一种改进的EEMD阈值去噪方法。该方法利用白噪声分解各分量能量密度与平均周期之积为常数这一特性对含噪信号进行“粗筛”，然后利用“3σ法则”和阈值去噪相结合的方式对含噪模态进行“细筛”，达到去噪效果的同时，也更好地保留了原始信号的细节信息，保持其原始特性。同时经实验验证，该方法在低信噪比下的去噪效果更为明显，所以其适用范围更广。结合该去噪方法，提出的基于二次EEMD分解的谐波检测方法在低信噪比情况下的检测效果更佳。

由于EEMD本身运算量很大，算法实时性的提高是本文去噪及谐波检测方法在今后需要更加完善的地方。

[1] 朱宁辉，白晓民，董伟杰 (Zhu Ninghui，Bai Xiaomin， Dong Weijie)．基于EEMD 的谐波检测方法 (Harmonic detection method based on EEMD) [J]．中国电机工程学报 (Proceedings of the CSEE)，2013，33(7)： 92-98．

[2] 张宇辉，段伟润，李云天 (Zhang Yuhui, Duan Weirun, Li Yuntian)．基于多级EEMD和WVD分布的谐波/间谐波检测方法(Method to detect harmonics and inter-harmonics based on multiple-level EEMD and Wigner-Ville distribution) [J]．电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2015，34(3)：66-71．

[3] 郑近德，程军圣，杨宇(Zheng Jinde，Cheng Junsheng， Yang Yu)．改进的EEMD算法及其应用研究(Modified EEMD algorithm and its applications) [J]．振动与冲击(Journal of Vibration and Shock)，2013， 32(21)：21-26．

[4] 张文忠，周蓉，武旭红，等 (Zhang Wenzhong，Zhou Rong，Wu Xuhong，et al.)．利用白噪声分解特征的EEMD阈值降噪方法(Threshold de-noising method based on the characteristics of white noise decomposed by EEMD) [J]．测绘科学技术学报 (Journal of Geomatics Science and Technology)，2013，30(3)： 255-259．

[5] 李利品，党瑞荣，樊养余 (Li Lipin，Dang Ruirong，Fan Yangyu)．改进的EEMD算法及其在多相流检测中的应用(Modified EEMD de-noising method and its application in multiphase flow measurement) [J]．仪器仪表学报 (Chinese Journal of Scientific Instrument)，2014，35(10)： 2365-2371．

[6] 苏立，南海鹏，余向阳，等 (Su Li，Nan Haipeng，Yu Xiangyang，et al.)．基于改进阈值函数的小波降噪分析在水电机组振动信号中的应用 (Application of wavelet denoising of improved threshold function to vibration signal analysis of hydroelectric units) [J]．水力发电学报(Journal of Hydroelectric Engineering)，2012，31(3)： 246-251．

[7] 刘晓光，胡静涛，高雷，等 (Liu Xiaoguang，Hu Jingtao， Gao Lei， et al.)．基于改进小波阈值的微机械陀螺去噪方法 (Micro mechanical gyro denoising method based on improved wavelet threshold) [J]．中国惯性技术学报(Journal of Chinese Inertial Technology)， 2014，22(2)： 233-236．

[8] 李洋，景新幸，杨海燕 (Li Yang，Jing Xinxing，Yang Haiyan)．基于改进小波阈值和EMD的语音去噪方法(Speech de-noising method based on empirical mode decomposition and improved wavelet threshold) [J]．计算机工程与设计(Computer Engineering and Design)，2014，35(7)：2462-2466．

[9] 樊刘娟，冯秀芳，朱晓军 (Fan Liujuan，Feng Xiufang， Zhu Xiaojun)．一种基于小波预处理的改进总体经验模态分解方法 (An improved ensemble empirical mode decomposition method based on wavelet pretreatment) [J]. 计算机测量与控制 (Computer Measurement & Control)， 2013，21(6)：1601-1604．

[10] 周二磊，张课，董苏 (Zhou Erlei， Zhang Ke， Dong Su)．基于EEMD阈值去噪的电能质量扰动检测研究(Power quality disturbance detection based on EEMD threhold denoising) [J]．华东电力 (East China Electric Power)，2013， 41(10)： 2090-2094．

[11] 魏利民，孙金宝，朱永利 (Wei Limin，Sun Jinbao，Zhu Yongli)． 基于EEMD的绝缘子泄露电流消噪方法(A de-noising method based on EEMD for insulator leakage current) [J]．华北电力大学学报 (Journal of North China Electric Power University)，2012，39(2)：17-22．

[12] 焦彦军，胡春 (Jiao Yanjun, Hu Chun)．基于改进EEMD方法的数字滤波器 (Digital filter based on improved EEMD method) [J]．电力自动化设备 (Electric Power Automation Equipment)，2011，31(11)：64-68．

[13] 卢丹，周以齐 (Lu Dan，Zhou Yiqi)．基于EEMD和CWT的挖掘机座椅振动分析 (Vibration analysis of excavator seat based on EEMD and CWT) [J]．山东大学学报 (Journal of Shandong University)，2015，25(2)：1-7．

[14] 余发军，周凤星 (Yu Fajun, Zhou Fengxing)．基于EEMD和自相关函数特性的自适应降噪方法 (Adaptive de-noising method based on EEMD and autocorrelation function property) [J]．计算机应用研究(Application Research of Computers)，2015，32(1)：206-209．

[15] 陈仁祥，汤宝平，马婧华 (Chen Renxiang，Tang Baoping，Ma Jinghua)．基于EEMD的振动信号自适应降噪方法(Adaptive de-noising method based on ensemble empirical mode decomposition for vibration signal) [J]．振动与冲击 (Journal of Vibration and Shock)，2012，31(15)：82-86．

[16] 王文波，张晓东，汪祥莉 (Wang Wenbo，Zhang Xiaodong，Wang Xiangli)．基于主成分分析的经验模态分解消噪方法(Empirical mode decomposition de-noising method based on principal component analysis) [J]．电子学报 (Acta Electronica Sinica)，2013，41(7)： 1425-1430．

[17] 郭奇，刘卜瑜，史立波，等 (Guo Qi，Liu Buyu，Shi Libo， et al.)．基于二次EEMD的Wigner-Ville分布旋转机械故障信号分析及试验研究 (Experimental study and fault signals analysis of rotating machinery based on dual EEMD and Wigner-Ville distribution) [J]．振动与冲击 (Journal of Vibration and Shock)，2012，31(13)：129-133．

[18] 马银戌，王文平，鄢小安，等 (Ma Yinxu，Wang Wenping，Yan Xiao’an，et al.)．基于二次EEMD的转子故障信号时频分析方法研究 (Study on time-frequency analysis method of rotor faults signal based on dual EEMD) [J]．科学技术与工程 (Science Technology and Engineering),2014，14(21)：113-117．

[19] 钟建军，宋健，由长喜，等 (Zhong Jianjun，Song Jian， You Changxi，et al.)．基于信噪比评价的阈值优选小波去噪法 (Wavelet de-noising method with threshold selection rules based on SNR evaluatios) [J]．清华大学学报(Journal of Tsinghua University)，2014，54(2)：259-263．

[20] Jialing Mo, Qiang He, Weiping Hu. An adaptive threshold de-noising method based on EEMD [A]. 2014 IEEE International Conference on Signal Processing, Communications and Computing, ICSPCC 2014 [C]. 2014. 209-214.

Study of improved EEMD denoising method and application in harmonic detection

SUN Shu-guang1, PANG Yi1, WANG Jing-qin2, ZHANG Chao3, DU Tai-hang1

(1. School of Control Science and Engineering, Hebei University of Technology, Tianjin 300130, China;2. School of Electrical Engineering, Hebei University of Technology, Tianjin 300130, China; 3. School of Electrical and Information Engineering, Shaanxi University of Science and Technology, Xi’an 710021, China)

To solve the modal mixing of EEMD in the decomposition process under low SNR, this paper proposes an improved EEMD threshold denoising method. Firstly, it uses the property that the product of energy density and average period for each IMF of white noise signal is constant after EEMD decomposition to determine the boundary point between useful signal and noise signal for roughly screening. Secondly, it screens the preceding modal with noise accurately. In the process, it uses“3σrules” to manipulate the first layer signal elaborately, there by retaining the details of the useful signal better and processes other modals with noise by way of energy estimation. Finally, it reconstructs the signal. Selecting SNR and MSE as the denoising effect standard, this method achieves the best denoising effect after experimental analysis, and the advantage is more obvious under low SNR. Based on the above denoising method, this paper further proposes a harmonic detection method based on the dual EEMD decomposition. The result shows that this detection method can detect the harmonic under low SNR and further proves the usefulness of this denoising method.

EEMD; threshold denoising;“3σrules”; dual EEMD decomposition; harmonic detection

2015-06-24

天津市科技支撑重点项目(12ZCZDGX014000)、河北省高等学校科学技术研究重点项目(ZD2014051)、河北工业大学博士科研启动费资助项目

孙曙光(1979-), 男, 河北籍, 副教授, 博士, 主要研究方向为谐波抑制以及无功补偿; 庞 毅(1990-), 男, 天津籍, 硕士研究生, 主要研究方向为谐波抑制以及无功补偿。

TM743

A

1003-3076(2016)04-0067-08