多机并网对孤岛检测方法的影响研究
2016-05-22王晓寰张纯江辛岩洁
王晓寰, 王 琳, 张纯江, 辛岩洁
(电力电子节能与传动控制河北省重点实验室, 燕山大学电气工程学院, 河北 秦皇岛 066004)
多机并网对孤岛检测方法的影响研究
王晓寰, 王 琳, 张纯江, 辛岩洁
(电力电子节能与传动控制河北省重点实验室, 燕山大学电气工程学院, 河北 秦皇岛 066004)
分布式发电系统并网运行时,孤岛检测是必须具备的功能。孤岛检测既要求快速准确,又要求尽量减少对电网造成的不良影响。随着大规模分布式发电系统的应用,尤其是微电网的出现,使得系统常连接多台并网逆变器,多逆变器并网系统孤岛检测技术的研究越来越受到关注。本文选取了三种典型孤岛检测方法进行研究,从盲区的角度分析了此三种孤岛检测方法对多机并网的适应性,以期为分布式发电多逆变器并网系统孤岛检测技术的研究奠定一定的理论基础和依据。
分布式发电; 多机并网逆变器; 孤岛检测
1 引言
现代人类文明发展面临的两大基本问题是能源短缺和环境污染,可再生的绿色能源成为解决人类能源需求和环境问题的希望。新能源中太阳能以其储量无限、清洁和经济等优势成为未来最有希望大规模应用的新能源之一[1]。孤岛检测是光伏逆变器并网控制系统必不可少的组成部分。“孤岛”是指公共电网停止供电后,由于分布式发电的存在(与电网连接并输送电能),使电网停电区部分线路仍维持带电状态,形成自给电力供应的孤岛[2]。然而,在孤岛状态下,电力公司将失去对线路电压、频率的控制,会带来一系列安全隐患。因此,电力公司要求并网的分布式发电系统必须及时检测出孤岛并断开分布式发电系统与公共电网间的连线。
目前,对于单机并网的孤岛检测无论是单相逆变器还是三相逆变器都有较多的研究,检测方法主要分被动检测法和主动检测法。被动孤岛检测方法是通过检测系统中电量的变化,如电压幅值、电压频率、功率变化率、谐波含量、电压电流相位等,不引入主动扰动[3-5]。这类检测方法简单易行,对电网电能质量无影响,但是盲区较大。主动检测方法是指在逆变器的控制变量中加入微小扰动,通过检测相应的输出量来判断孤岛,微小扰动包括电流幅值、频率、相位扰动,有功功率和无功功率扰动、谐波注入等[6-8]。这类孤岛检测方法检测盲区小,甚至没有检测盲区,但是其扰动信号会破坏电网的电能质量。
随着国家政策对分布式发电并网的逐渐开放,无论是户用分布式发电系统的并网还是微电网并网运行,都有多机并网的特性,现有的孤岛检测方法一般对单机并网情况下的研究比较深入,在多机并网情况下,较少有文献谈及其对孤岛检测方法的影响。本文选取了三种常见的孤岛检测方法:①被动孤岛检测方法中的过/欠压(OVP/UVP)、过/欠频(OVF/UVF)法,②主动孤岛检测方法中的主动电流扰动法,③带正反馈的主动移频(AFDPF)孤岛检测方法,从分析检测盲区的角度对其进行了多机并网适应性的研究,并进行了相应仿真验证。
2 被动孤岛检测方法多机并网适应性分析
2.1 过/欠压、过/欠频孤岛检测方法的模型建立
本文采用单相并网逆变器为研究对象,单位功率因数并网,并采用恒流控制策略。并网逆变器功率关系如图1所示。
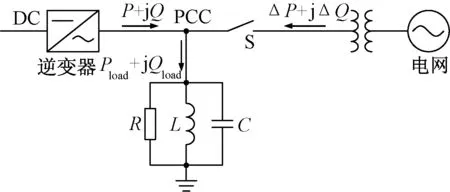
图1 并网逆变器功率关系图Fig.1 Grid-connected inverter power diagram
过/欠压与过/欠频孤岛检测方法是最常用的两种被动孤岛检测方法,对其建立数学模型。逆变器并网运行时,根据功率平衡,负载的功率等于逆变器输出功率与电网提供功率之和,得到功率关系式:
(1)
式中,Pload为负载有功功率(W);Qload为负载无功功率(var);P为逆变器输出有功功率(W);Q为逆变器输出无功功率(var);ΔP为电网提供有功功率(W);ΔQ为电网提供无功功率(var)。
逆变器输出的有功功率和无功功率可表示为:
(2)
式中,VPCC为公共耦合点电压(V);IP为逆变器输出有功电流(A);Vg为电网电压(V);IQ为逆变器输出无功电流(A)。
并联负载RLC的有功功率和无功功率可表示为:
(3)
式中,R为负载电阻(Ω);L为负载电感(H);C为负载电容(F);ω为电网电压角频率(rad/s)。
断网后逆变器孤岛运行时,由于采用单位功率因数恒流控制,系统在负反馈的作用下稳定运行后,逆变器工作在负载的谐振频率点,负载成阻性,PCC点电压和频率变为:
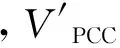
如果断网后,PCC点电压没有超出电网电压允许的稳定运行范围[Vmin,Vmax],那么OVP/UVP孤岛检测方法失败。此方法的孤岛检测盲区可以表示为:
(6)
将式(6)代入GB/T19939-2005所规定稳定运行的电压范围88%~110%,于是OVP/UVP孤岛检测的检测盲区运用有功功率和无功功率适配空间盲区表示法可以表示为:
(7)
由式(5)变换可以得到,断网后孤岛运行稳定时的频率可以表示为:
(8)
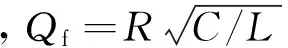
如果断网后,PCC点电压频率没有超出电网电压允许的稳定运行频率范围[fmin,fmax],那么OVP/UVP孤岛检测方法失败。则此方法的孤岛检测盲区可以表示为:
(9)
根据IEEE Std.929-2000中所允许的正常运行频率范围(49.3Hz,50.5Hz),可以得到OVF/UVF方法的检测盲区,运用有功功率和无功功率适配空间盲区表示法可以表示为:
(10)
根据式(9)和式(10)得到过/欠压、过/欠频的组合盲区,如图2所示。随着品质因数的增加盲区逐渐增加。
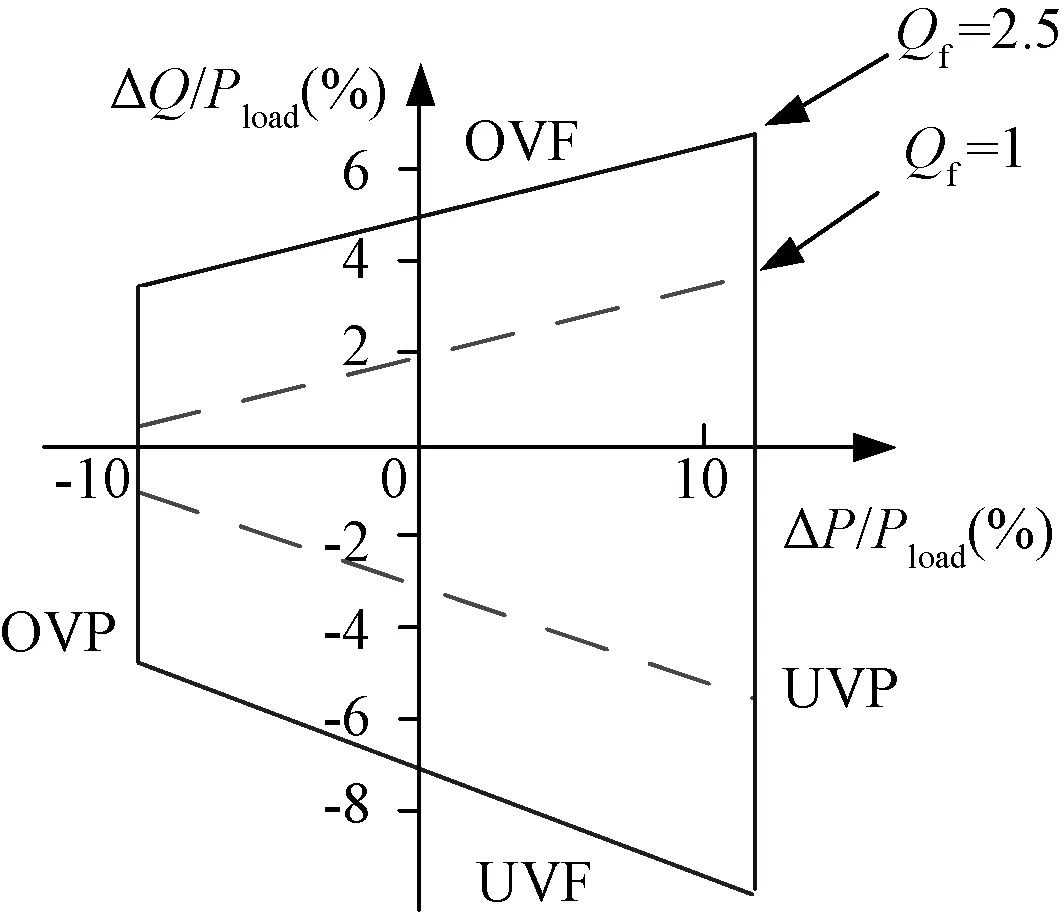
图2 过/欠压、过/欠频的组合盲区Fig.2 OVP/UVP non-detected zone
2.2 过/欠压、过/欠频孤岛检测方法对多机并网适应性分析
当多台分布式发电系统并入同一段大电网时,各自的输出功率是一定的,分别为P1,…,Pn、Q1,…,Qn;各自所带的负载分别为R1,…,Rn、L1,…,Ln、C1,…,Cn;负载功率分别为P1load,…,Pnload、Q1load,…,Qnload。当大电网断网后,系统等效为多个带各自负载的DG并联。逆变器总的输出功率为:
PΣ=P1+P2+…+Pn=(I1+I2+…+In)Vg
(11)
式中,I1,…,In为各逆变器的输出有功电流(A)。
并联负载为:
(12)
(13)
CΣ=C1+C2+…+Cn
(14)
电网断电后,由于多机系统都是恒流控制,重新达到稳定后得到:
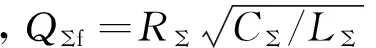
式(15)和式(16)表明,在孤岛稳定运行的情况下,多机并联和单机在断网后运行时电压幅值和频率的计算结果形式相同,只是在功率处将单机功率换成多机功率之和,负载品质因数换成多负载并联的品质因数,因此在讨论盲区时可得:
(17)
由盲区表达式(17)可知,多机与单机并网对OVP/UVP和OVF/UVF孤岛检测方法的盲区本质是一致的,多机时的判断依据变为多逆变器系统输出功率之和与对应的负载之和的匹配程度。
3 主动电流扰动孤岛检测方法对多机并网适应性分析
3.1 主动电流扰动孤岛检测方法的模型建立
为了解决过/欠压孤岛检测方法中存在检测盲区的问题,很多文献中提出采用电流幅值扰动的孤岛检测方法。为了减小对电能质量的影响,一般都取每隔n个正常电流输出周期,添加一个或者两个扰动周期,断网之后,在未加入扰动的周期,由于负载匹配程度比较好,无法检测出孤岛。合理设置扰动的幅值,可以使得该方法在任何情况下都能够检测出孤岛,实现无盲区检测。
文献[9]通过对三相并网逆变器孤岛运行建模,得到在三相并网逆变器断网后,重新达到稳定运行后的模型:
(18)
式中,Id为有功电流(A);Iq为无功电流(A)。
从式(18)可以看出,重新稳定后的电压仅与有功电流相关,电压的频率与有功电流、无功电流、负载品质因数以及负载的谐振频率都相关,但是采用单位功率因数并网稳定运行时,频率为负载的谐振频率。
仍采用单位功率因数并网,给定电流为:
(19)
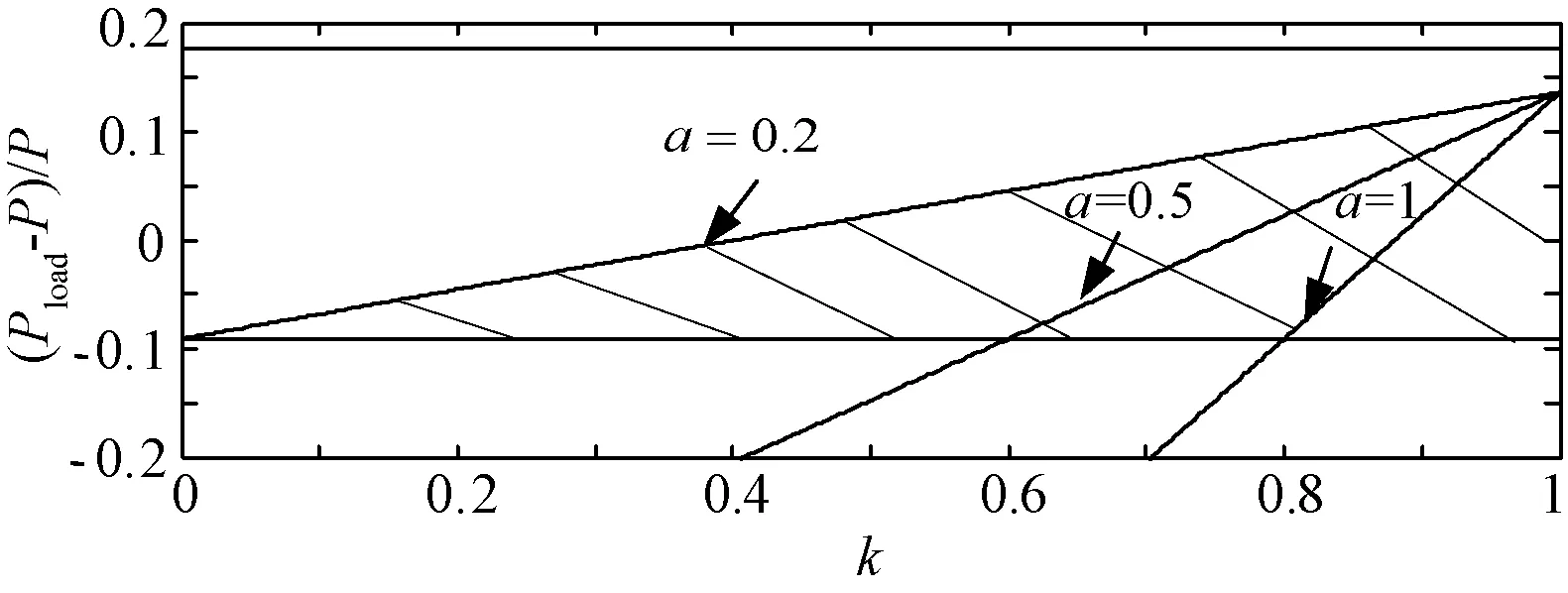
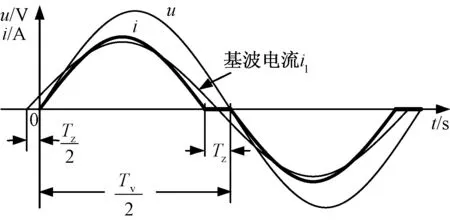
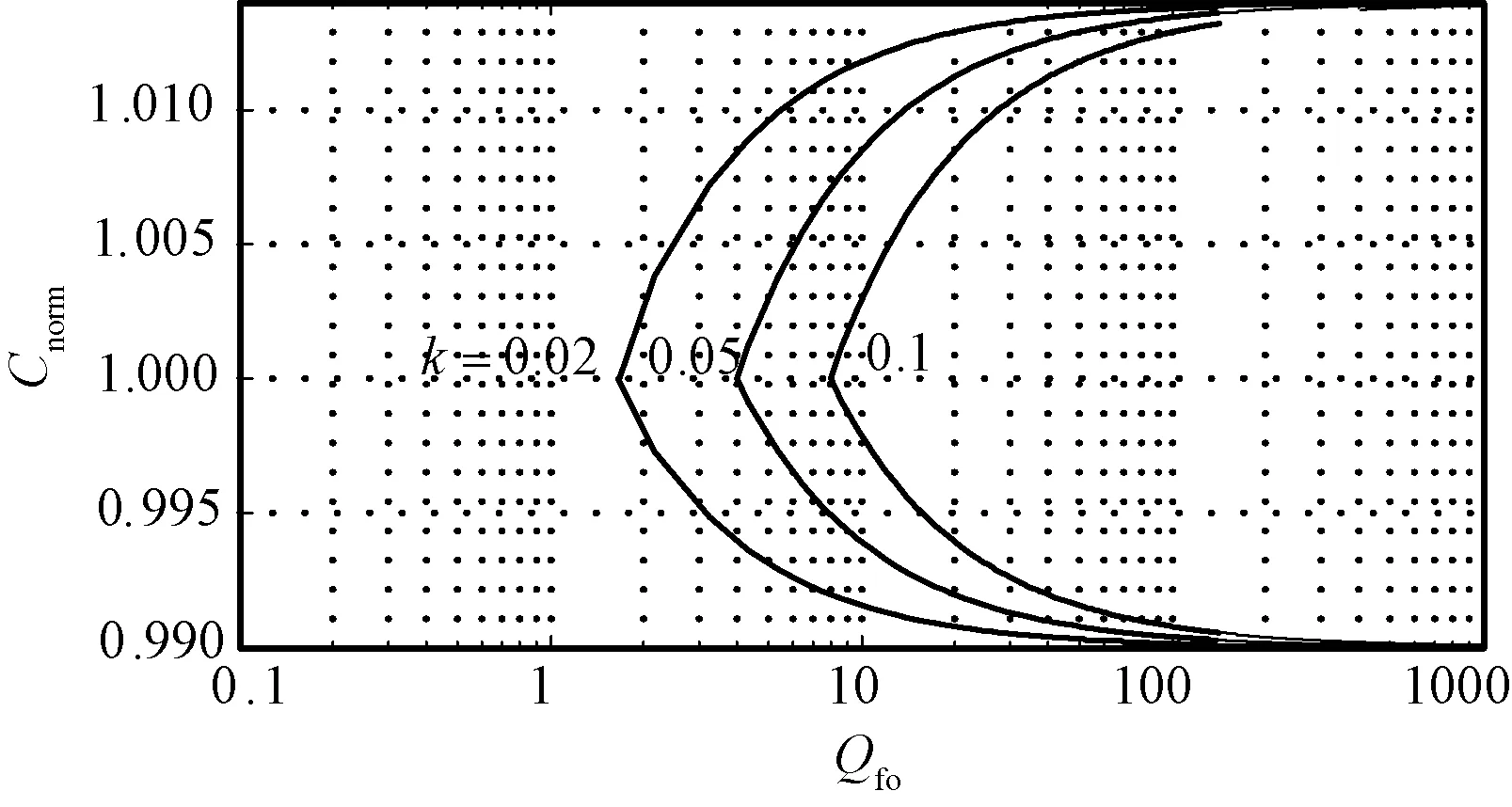
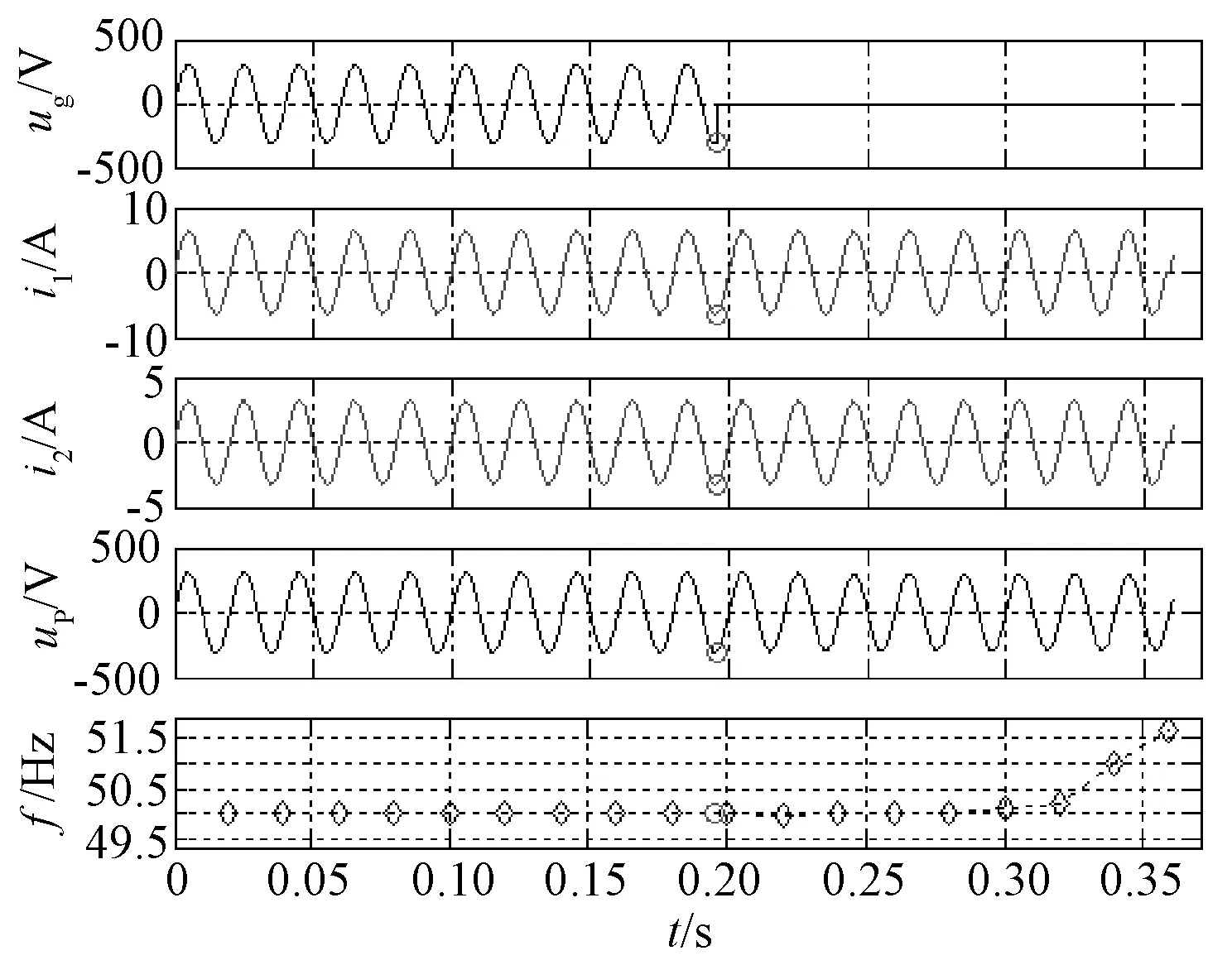
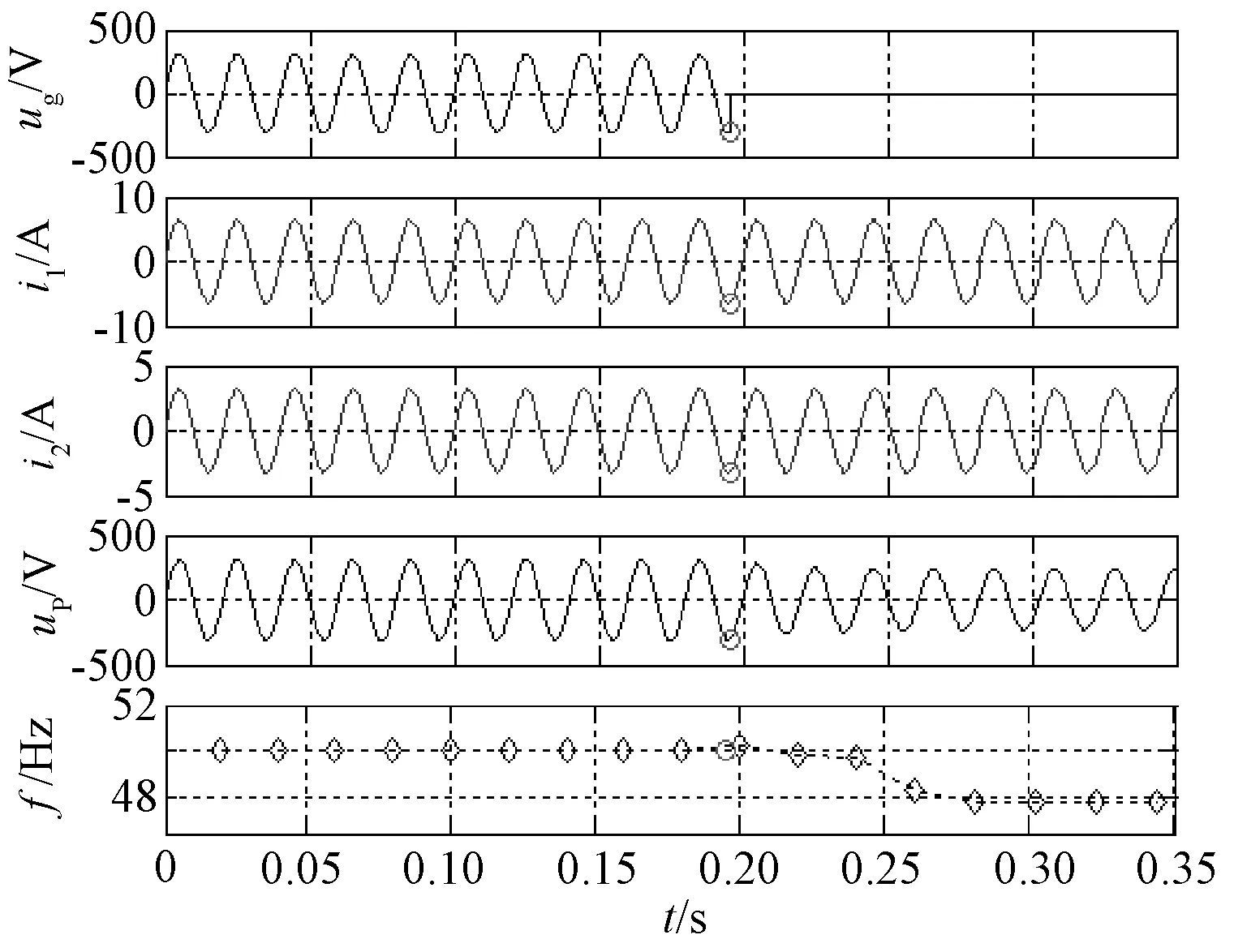
式中,k为主动电流扰动检测方法的扰动系数,为了减小系统由于过流可能造成的设备或负载损害,一般取0 (20) 整理后,用有功功率表示为: (21) 根据式(21)得到主动电流扰动法的盲区仿真图如图3所示。从仿真结果可知,主动电流扰动法的检测盲区 (Non-DetectedZone,NDZ)明显小于过/欠压孤岛检测方法,当k<0.8时,便可以实现无盲区。 图3 主动电流扰动法盲区图Fig.3 Non-detected zone of active current perturbation method 3.2 主动电流扰动孤岛检测方法对多机并网适应性分析 多机情况下,由于不同控制器中扰动周期的不同步将导致扰动之间的相互削弱即稀释效应。假设在某一时刻,逆变器A达到扰动周期,而其它并网逆变器并未达到扰动周期,那么设定: (22) 式中,I1为逆变器A的有功电流(A);IΣ为剩余逆变器有功电流之和(A);a为逆变器A有功电流占总线路电流的比例系数。 断网后PCC点电压跟随电流给定,在扰动周期和非扰动周期呈现不同的幅值。在某段时间内的值为: (23) 按照2.1节所述对稳定运行的电压幅值要求规定,逆变器A的检测盲区可以表示为: (24) 将式(22)代入式(24)中,可以得到盲区为: (25) 根据式(25)仿真得到主动电流扰动法在多机并网下的检测盲区,如图4所示。 图4 主动电流扰动法在多机并网下的盲区示意图Fig.4 Non-detected zone of active current perturbation method with multi-inverter 若使此方法在多机情况下无检测盲区,那么需满足: (26) 解得: (27) 针对多逆变器在某一时刻只有一个逆变器达到扰动周期,而其它并网逆变器并未达到扰动周期的情况,由计算结果和检测盲区图4得到如下结论: (1)当a≤0.2时,无法通过选择一个合适的k值使得系统检测无盲区; (2)当0.2≤a≤1时,即逆变器A的容量占总逆变器容量的20%以上,且当k<1-0.2/a时,才能够保证系统达到检测无盲区。 但是,为了减小孤岛检测方法对电能质量的影响,k不可能无限小;而且也难以保证一定存在逆变器额定容量满足0.2≤a≤1,所以电流扰动孤岛检测方法对于多机并网情况显现出一定的不适应性。与单机情况相比,多机情况孤岛检测盲区明显增加,很容易受到每台DG容量在总并联逆变器容量所占比例的影响,并且不能通过改变扰动参数保证无盲区。 4.1 AFDPF孤岛检测方法的模型建立 引入频率偏移的并网逆变器输出电流波形如图5中粗实线所示。其中Tv为PCC点电压周期,tz为引入频率偏移产生的死区时间,定义截断系数cf为: (28) 可见,当并网逆变器控制采用引入频率偏移量的电流波形时,逆变器输出电流i中的基波成分i1将始终超前电流给定基准信号一个相位角ωvtz/2。 图5 主动移频算法波形图Fig.5 Waveforms of AFDPF AFDPF是加入正反馈的主动移频算法,与主动移频算法AFD的区别在于截断系数cf可变,根据PCC点电压频率与电网电压频率的偏差引入正反馈,其表达式为: cf=cfo+k(f′-f) (29) 式中,cfo为初始截断系数;f′为PCC点电压频率(Hz);f为电网电压频率(Hz)。 断网后,电压的频率将是电流频率与负载性质共同作用的结果。若负载不是纯电阻负载,那么断网后系统将重新建立稳定工作状态,此状态满足: (30) 若此时ω′没有超出额定电网频率所允许的稳定运行范围,那么此方法将无法检测出孤岛状态,形成检测盲区,由此求得盲区表达式为: (31) 式中,Qfo为准品质因数,Qfo=R/(ωL),表示L一定,谐振频率等于电网频率时的品质因数;Cres为准电容,Cres=1/(Lω2),表示L一定,谐振频率等于电网频率时所需电容的值;Cnorm为电容系数,Cnorm=C/Cres。 将式(29)代入式(31),并令cfo=0,得到: (32) 根据式(32)得到Qfo×Cnorm盲区描述法表示的检测盲区图,如图6所示。 图6 AFDPF孤岛检测方法的检测盲区Fig.6 Non-detected zone of AFDPF 由图6可知,k越大盲区越小,因此可以通过改变k调节盲区的大小,若k足够大可以消除盲区,但会增大对电网的影响。 4.2 AFDPF孤岛检测方法对多机并网适应性分析 假设两台逆变器均使用AFDPF的孤岛检测方法,其电流给定波形基波与其过零点的移相角为ωtz/2,如果tz很小,电流谐波很小,那么逆变器输出电流与公共点电压相位差可表示为: (33) 那么下一时刻的电流给定基波可以表示为: IAFDPF=Isin(2πft+θAFDPF) (34) 由于两台逆变器并入同一段电网,因此前一时刻的PCC点频率是相同的,可以认为,下一时刻电流基波频率是相同的,不同的只是因为引入频率反馈系数导致等效位移相角不同,于是可以得到两台逆变器下一时刻的电流给定分别为[10]: I1(k)=I1sin[2πf(k-1)t+θ1(k)] (35) I2(k)=I2sin[2πf(k-1)t+θ2(k)] (36) 则负载上的总电流为: (37) 可以得到: (38) 由推算结果可知,当两台并联逆变器都使用AFDPF孤岛检测方法时,只要保证每台单机逆变器能够实现孤岛检测,多机系统便可以实现。 采用Matlab/Simulink对两台均采用AFDPF孤岛检测方法的逆变器进行仿真。仿真中设定第一台逆变器功率为1000 W,第二台逆变器功率为500W;负载消耗的有功功率与逆变器输出功率相匹配即R1=48.4Ω,R2=96.8Ω;电感和电容恰好在电网频率处谐振,L1=L2=6.16mH,C1=C2=0.164mF。两台逆变器均采用AFDPF算法检测孤岛,负载平衡情况下的仿真波形如图7所示。负载不平衡情况时,设定R1=35Ω,R2=100Ω,C1=0.169mF,C2=0.163mF,该情况下的仿真结果如图8所示。 对于非平衡谐振负载,断开并网开关后,节点电压幅值发生变化,而且该方法在更短的时间内使节点电压频率超出过/欠频保护范围,检测出孤岛的发生。仿真验证了该方法对于对多台并联系统的有效性。 图7 对平衡谐振负载的多机系统孤岛检测仿真结果Fig.7 Simulation result for balance resonance load 图8 对非平衡谐振负载的多机系统孤岛检测仿真结果Fig.8 Simulation result for none balance resonance load 通过对过/欠/压、过/欠频被动孤岛检测方法,主动电流扰动和主动移频孤岛检测方法的盲区分析和在多机并网情况下适应性的分析,得出以下结论:①被动孤岛检测方法的盲区相对较大,其大小与负载的品质因数相关,品质因数越大,盲区越大;②被动孤岛检测方法在多机并网的情况下,不影响其检测盲区范围,可以与主动孤岛检测方法相结合应用于多机并网的情况;③主动电流扰动孤岛检测方法在单机的情况下可以通过调节扰动系数k,实现无检测盲区,在多机并网的情况下,由于扰动周期不同步,使得此时盲区变大,此方法不适合多机并网的情况;④AFDPF是带正反馈的频率扰动孤岛检测方法,由于此类方法具有自适应性和正反馈,所以在多机的情况下与单机无区别,但是AFDPF依赖于过零点检测,并且只适合于单相逆变器,在三相系统中实现复杂。因此多机并网的主动孤岛检测方法应该具备扰动同步和扰动的自适应正反馈两个特点。 [1] 郭晓瑞, 郭吉丰 (Guo Xiaorui, Guo Jifeng). 单相光伏并网逆变控制器的优化 (Optimization of controller for single-phase grid-connected photovoltaic inverters) [J]. 电工电能新技术 (Advanced Technology of Electrical Engineering and Energy), 2013, 32(4): 40-43, 64. [2] IEEE Std 1547-2003, IEEE standard for interconnecting distributed resources with electric power systems[S]. [3] 张有兵, 穆淼婕, 翁国庆(Zhang Youbing,Mu Miaojie,Weng Guoqing). 分布式发电系统的孤岛检测方法研究(Research on islanding detection of distributed power generation systems)[J]. 电力系统保护与控制(Power System Protection and Control), 2011, 39(6): 140-146. [4] 程启明, 王映斐, 程尹曼, 等 (Cheng Qiming, Wang Yingfei, Cheng Yinman, et al.). 分布式发电并网系统中孤岛检测方法的综述研究 (Overview study on islanding detecting methods for distributed generation grid-connected system) [J]. 电力系统保护与控制(Power System Protection and Control), 2011, 39(6): 147-154. [5] 王晓寰,张修北,董杰,等 (Wang Xiaohuan, Zhang Xiubei, Dong Jie, et al.). 基于0-1序列的三相并网逆变器孤岛检测方法 (Study of an active islanding detection method based on 0-1 sequence for three-phase gird-connected inverter) [J]. 电源学报 (Journal of Power Supply),2014,(6):86-92 [6] 郭小强, 赵清林, 邬伟扬 (Guo Xiaoqiang, Zhao Qinglin, Wu Weiyang). 光伏并网发电系统孤岛检测技术(Islanding detection method for photovoltaic grid-connected power system) [J]. 电工技术学报(Transactions of China Electrotechnical Society), 2007, 22(4): 157-162. [7] L A C Lopes, Huili Sun. Performance assessment of active frequency drifting islanding detection methods [J]. IEEE Transactions on Energy Conversion, 2006, 21(1): 171-180. [8] H H Zeineldin, E F El-Saadany, M M A Salama. Impact of DG interface control on islanding detection and nondetection zones [J]. IEEE Transactions on Power Delivery, 2006, 21(3):1515-1523. [9] 杨秋霞, 赵清林, 郭小强 (Yang Qiuxia, Zhao Qinglin, Guo Xiaoqiang). 三相光伏并网逆变器电流扰动孤岛检测建模及分析(Modeling and analysis of current-disturbance based islanding detection for three-phase photovoltaic grid-connected inverters) [J]. 电力系统自动化(Automation of Electric Power Systems), 2012, 36(4): 45-49. (,cont.onp.74)(,cont.fromp.66) [10] 刘方锐, 段善旭, 康勇, 等 (Liu Fangrui, Duan Shanxu, Kang Yong, et al.). 多机光伏并网逆变器的孤岛检测技术(Islanding detection methods for multiple PV converters system) [J]. 电工技术学报(Transactions of China Electrotechnical Society), 2010, 25(1): 169-171. min(θ1,θ2)<θ Research of effect on islanding detection methods of multi-inverter connected to grid WANG Xiao-huan, WANG Lin, ZHANG Chun-jiang, XIN Yan-jie (Key Lab of Power Electronics for Energy Conservation and Motor Drive of Hebei Province, College of Electrical Engineering, Yanshan University, Qinhuangdao 066004, China) Islanding detection is one of the necessary functions of grid-connected distributed generation system. It requires that not only to detect the islanding state fast and accurately, but also to minimize the adverse impact on the grid. There would be more than one inverter connected to the system with the application of large-scale distributed generation system, especially with appearing of microgrid. The study of islanding detection of multi-inverter grid-connecting system is drawing more and more attention. In this paper, three major islanding detection methods are selected to analyze the effect of multi-inverter connected to the grid from the point of non-detection zone. It establishes certain theoretical basis for the study of islanding detection of multi-inverter grid-connecting system. distributed generation; multi-inverter; islanding detection method 2015-04-28 河北省高校青年基金(QN2014183)、燕山大学青年基金(14LGB010;15LGB012)、河北省自然科学基金(E2016203357)资助项目 王晓寰 (1980-), 女, 河北籍, 副教授, 博士, 研究方向为并网逆变器控制; 张纯江 (1961-), 男, 黑龙江籍, 教授, 博士, 研究方向为分布式发电控制(通信作者)。 TP29 A 1003-3076(2016)04-0061-06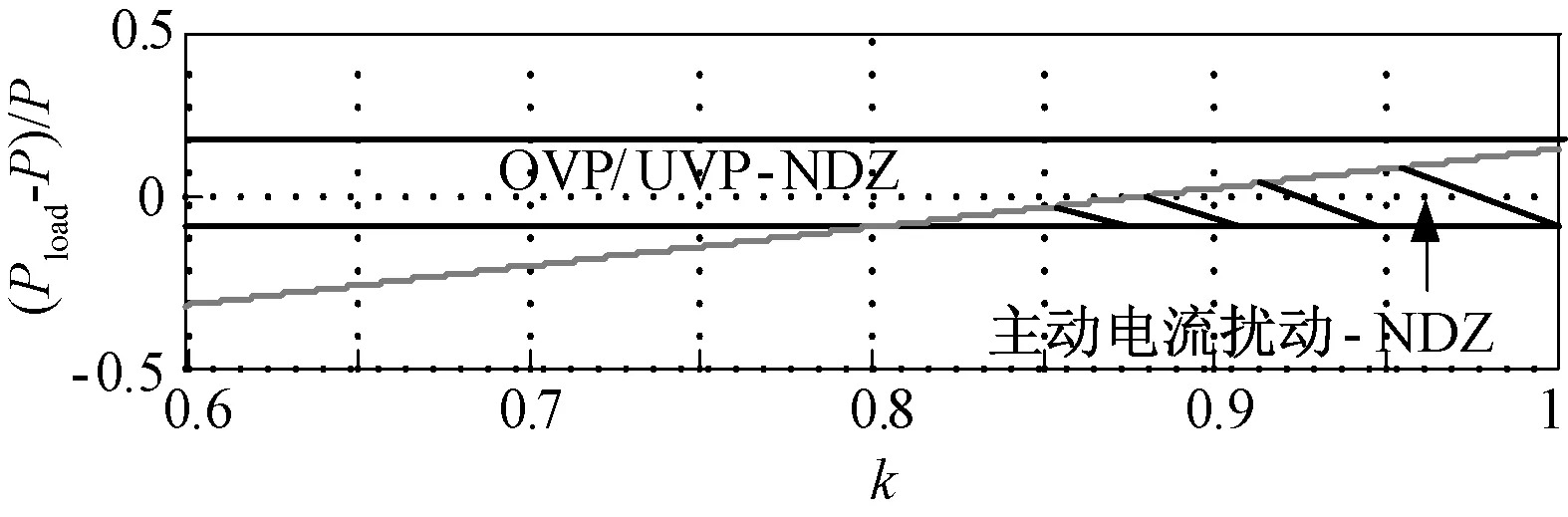
4 带正反馈的主动移频孤岛检测方法对多机并网适应性分析
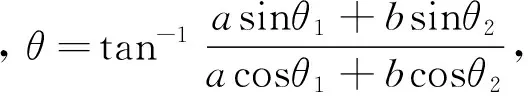
5 仿真验证
6 结论
