钢筋混凝土双向压弯构件正截面承载力简化计算

刘春阳，王萌

（山东建筑大学土木工程学院，山东 济南 250101）

钢筋混凝土双向压弯构件正截面承载力简化计算

刘春阳，王萌

（山东建筑大学土木工程学院，山东 济南 250101）

框架柱双向压弯承载力不足是导致地震发生时结构严重破坏甚至倒塌的原因之一。文章基于截面等效的方法，在不改变截面面积、混凝土受压区面积以及截面等效前后对中和轴面积矩相等的条件下，得到框架柱双向压弯承载力计算用等效截面，同时基于平衡原理建立了双向压弯承载力简化计算方法，利用简化计算方法和等效梭形法对空间节点试验中框架柱的双向压弯承载力进行了计算，在保持配筋数量和截面几何参数不变的条件下考虑了纵筋分别向角筋偏移2倍钢筋直径、4倍钢筋植筋和与角筋紧密接触三种情况来探索提高截面双向压弯承载力的方法。结果表明：两种方法所得结果与试验实测值均符合较好，且简化方法计算精度较高，与试验实测值仅相差3%；随着纵筋向角筋的偏移，框架柱截面双向压弯承载力明显提高，提高幅度在 14%～42%。

钢筋混凝土柱；双向压弯；承载力；简化计算；截面等效

0 引言

框架柱是结构中重要的承重构件，但震害调查发现框架柱在地震中极易产生损伤甚至破坏而影响结构的安全使用［1－5］。地震作用具有多维性和任意性特点，结构的任意方向都有可能是其主要作用方向也即最不利作用方向，当地震作用沿斜向（非主轴）方向作用于结构时，框架柱便处于双向压弯的不利受力状态，而现行结构设计方法只进行结构两主轴平面内的承载力验算并没有考虑框架柱截面双向压弯强度验算是造成框架柱破坏的原因之一［6－9］。钢筋混凝土双向压弯构件正截面承载力计算方法的研究已有很多年，许多学者给出了相应的计算方法，有的已写入设计规范用以指导实际工程设计。Bresler和Alfred指出框架柱双向压弯受力时的破坏荷载与柱子截面尺寸、钢筋的数量和分布特征、钢筋和混凝土的应力—应变关系以及混凝土保护层厚度、箍筋的布置等因素有关［10－11］。精确的计算公式难以得到，但通过分析可以得到破坏荷载与框架柱两主轴方向极限弯矩的相关曲面（又称破坏曲面），并给出了任意给定轴力下相关曲面的包络线曲线方程用以计算框架柱双向压弯正截面承载力。对于一个承受双向压弯作用的截面来讲，每一个轴力弯矩组合都会对应一个中和轴位置，因此可以通过尽可能多的轴力弯矩组合去确定尽可能多的中和轴的位置，这就为设计曲线法的建立奠定了基础。Fleming与 Tung首先基于不同轴力弯矩组合通过迭代计算确定中和轴的位置也即确定了混凝土受压区形状，其次通过截面平衡条件建立双向压弯时构件极限轴力和轴力在两主轴方向的偏心距表达式，进而针对常用矩形（方形）截面形式、混凝土强度等级、钢筋强度和配筋率等设计参数绘制了一单列无量纲设计用曲线［12－13］。通过无量纲设计曲线可较快的确定双向压弯构件截面尺寸和配筋，减少了设计人员设计所需时间。该方法虽可简化设计过程，但只是针对钢筋混凝土结构常用截面形式给出的设计曲线，随着高层建筑结构的发展，构件截面形式将会变的更加复杂，高强度钢筋和高强度混凝土以及组合结构等也会得到大量应用，设计曲线的确定将会变的更加复杂。基于纤维模型法的双向压弯构件正截面承载力计算方法，首先将截面划分为有限多个混凝土单元、纵向普通钢筋单元，并近似取单元内的应变和应力为均匀分布，其合力点在单元重心处，每种材料纤维采用相应的本构关系且能考虑两主轴方向弯矩之间的耦合。该方法虽能考虑两主轴方向弯矩之间的耦合，但材料本构关系的设定对计算结果精度的影响较大，且需借助数值积分方法确定其正截面 强度［14－16］。此外，GB 50011—2010《混凝土结构设计规范》还给出了双向偏压构件受压承载力的近似公式［15］，形式简单但在偏心距较大的情况下计算误差较大，同时该计算方法未能反映构件截面的实际受力状态，与单向偏压受力情况的计算方法未能很好的相互协调，只能近似的对轴压极限承载力进行验算而无法得到真实的轴压承载力。宋坤等基于正截面承载力计算的数值积分法原理，通过对极限状态下构件截面应变分布特征的分析，提出了从极限状态下的应变分布出发逆向计算双向压弯构件正截面强度的方法［17］。通过 2重循环计算极限状态时的截面内力，不仅减小了现有正向积分方法确定截面极限承载力的计算量和计算时间，也可解决小偏心受压构件的极限承载力确定问题。与试验实测结果的对比表明，逆向正截面承载力计算方法误差较小，计算精度较高，具有较好的实用性［17－18］。双向压弯构件正截面强度计算的复杂性，主要是由于中和轴与截面边缘斜交而引起的。由于双向压弯构件截面中和轴倾斜，受压区形状较为复杂，从而在确定受压区面积和受压区压力合力点位置时非常困难。Mattock将任意配筋矩形截面双向压弯构件的受压区形状划分为三角形、梯形和五角形三种情况，其中梯形受压区又分中和轴与矩形短边相交、中和轴与矩形长边相交两种情形，对应不同的受压区形状按照构件截面内力与所受外力平衡的原理给出了相应的计算公式［19］。该方法虽理论明确，但需通过迭代计算确定中和轴的最终位置后才能计算截面承载力，迭代计算需要编写相应的计算程序而使得该方法在实际工程设计时难以被采用。等效梭形截面法最早由东南大学提出，用于双向受弯构件的正截面承载力计算；陈忠汉等利用截面等效的方法将矩形截面转化为梭形截面，进而将双向压弯构件的强度计算问题转化为单向压弯受力状态下的强度计算并给出了相应的计算方法，其计算结果和试验结果符合程度较好［20－21］。文章在钢筋混凝土框架空间节点试验研究的基础上对框架柱的双向压弯强度简化计算方法进行了研究［22］。

1 等效截面

图1（a）所示为处于双向压弯受力状态的矩形框架柱截面，假定等效截面与原有截面具有相同的截面面积，相同的混凝土受压区面积且等效前后对中性轴的面积矩相等，将双向压弯受力的矩形截面等效为梭形截面，如图 1（b）所示，再在梭形的四个角上增加一个小三角形使其变为一个矩形，同时在矩形的四个角部各加一个与前述小三角形形状相同但面积为负的小三角形，适当的选择矩形翼缘的宽和高，使得负矩形翼缘的面积及其形心位置与所添加负三角形的面积和形心位置相同，得到一个负工字形截面，如图 1（c）所示，再把负矩形翼缘与相邻截面合并后得到文中等效截面，如图1（d）所示。等效截面的尺寸可按式（1）～（3）确定为

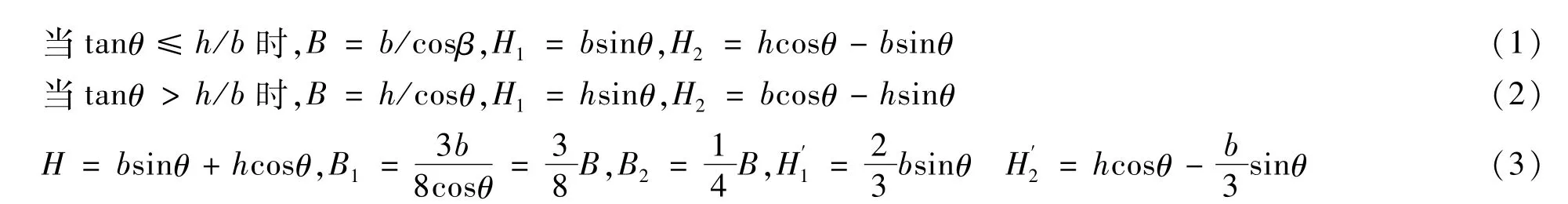
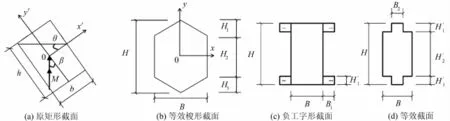
图1 等效截面示意图

式中：β为压弯作用平面与截面主轴（y′）平面夹角，°；θ为截面中和轴与截面主轴（x′）夹角，可按 θ＝确定，当β＝0时，θ＝0，而此时中和轴平行于主轴（x′）即为单向压弯受力状态；b和h分别为原截面宽度和高度，mm；B和 H分别为等效截面的宽度和高度，mm；H1和H3分别为等效梭形截面两端三角形部分的高度，mm，H2为等效梭形截面中间矩形部分的高度，mm；B1和H′1分别为负矩形翼缘的宽度和高度，mm；B2和H′2分别为等效截面翼缘宽度和中间矩形部分高度，mm。

原截面钢筋在截面转换后沿中和轴方向平行移动到等效截面的对称轴处，其位置可由式（4）确定为

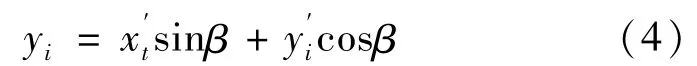
式中：x′i和 y′i分别为钢筋在原截面的坐标值；yi为钢筋在等效截面中的纵坐标值［23－25］。

2 双向压弯构件正截面承载力简化计算

2.1 正截面承载力简化计算方法

为了简化起见，正截面承载力计算时假定（1）截面应变符合平截面假定；（2）不考虑受拉区混凝土的作用；（3）混凝土与钢筋的应力 — 应变关系按GB 50011—2010《混凝土结构设计规范》的相关规定执行［15］；（4）纵向受力钢筋的极限应变取为0.01；（5）受压区混凝土应力图形为矩形应力图形。等效截面正截面承载力计算简图如图2所示。框架柱截面处于双向压弯受力状态并达到极限承载力时应满足静力平衡条件，因此可以根据平衡原理建立纵向力平衡方程与弯矩平衡方程并分别由式（5）、（6）表示为

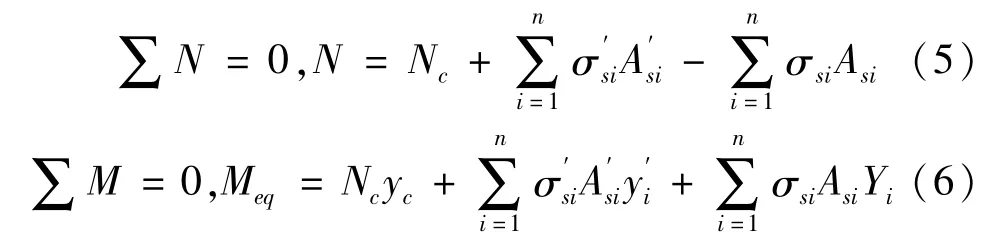
弯矩平衡方程（6）通过受拉区各钢筋所受拉力、受压区各钢筋所受压力以及受压区混凝土合力对等效截面形心取矩的方式建立。

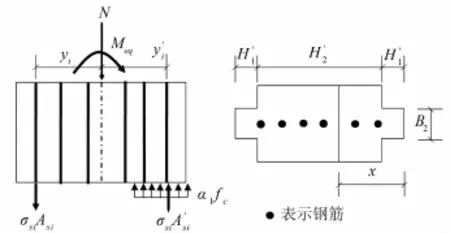
图2 文章方法正截面承载力计算简图

式中：σsi为受拉区第i根钢筋应力，N／mm2；Asi为受拉区第 i根钢筋面积，mm2；σ′si为受压区第 i根钢筋应力，N／mm2；A′si为受压区第 i根钢筋面积，mm2；N为框架柱截面压力设计值，kN；Nc为受压区混凝土合力，kN。计算时首先假设受压区高度（x）为 H1′，确定受压区钢筋数量和各钢筋所受压力合力、受拉区钢筋数量和各钢筋所受拉力合力以及受压区混凝土压力合力，代入式（7）后如果不等式关系成立，则受压区高度（x）在 H1′范围内，否则进入 H2′范围内，应重新确定受压区高度和受力纵筋的应力；yc为受压区混凝土合力作用点到等效截面形心的距离；Meq为等效截面正截面承载力，M为原截面正截面承载力，kN·m。Meq与 M满足式（8）所示关系。

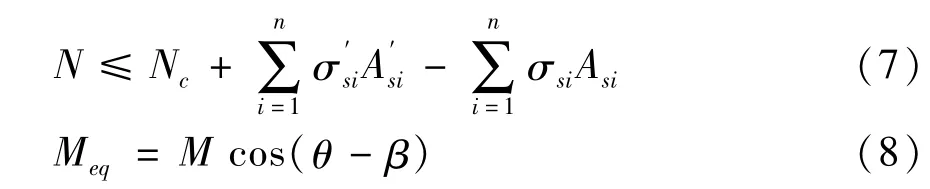
2.2 等效梭形截面法

利用等效梭形法计算正截面承载力时仍可采用2.1节基本假定，且其计算简图如图3所示。根据静力平衡条件可分别建立轴向力平衡方程和弯矩平衡方程。其中，轴向力平衡方程仍采用2.1中的式（5）表示，弯矩平衡方程通过截面上轴向力与受压区混凝土压应力合力以及各受压钢筋受力对受拉钢筋合力点取矩的方式建立，可用式（9）表示为

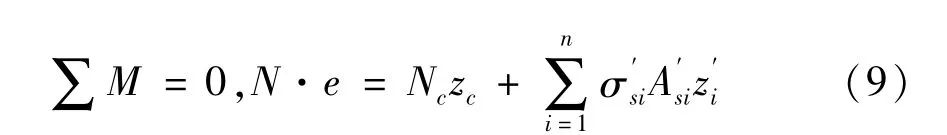
式中：e为轴向力N到等效截面中受拉钢筋合力点的距离，mm；zc为受压区混凝土压应力合力作用点到受拉钢筋合力点的距离，mm；z′i为第 i根受压钢筋到受拉钢筋合力点的距离，mm。计算时首先假设受压区高度（x）为 H1，确定受压区钢筋数量和各钢筋所受压力合力、受拉区钢筋数量和各钢筋所受拉力合力以及受压区混凝土压应力合力，代入式（7）后如果不等式关系成立，则受压区高度（x）在H1范围内，否则进入 H2范围内，应重新确定受压区高度和受力纵筋的应力。

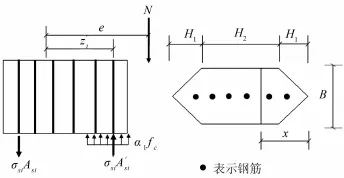
图3 梭形法正截面承载力计算简图

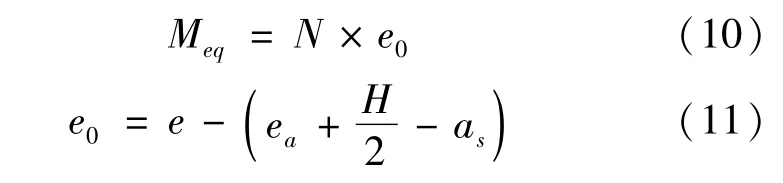
式中：ea为附加偏心距，mm；as为等效截面受拉钢筋合力点到截面顶点的距离，mm。

2.3 承载力计算结果对比分析

钢筋混凝土框架中柱空间节点中框架柱采用方形截面，截面尺寸及纵筋布置方式如图 4（a）所示，纵筋采用直径为16 mm的HRB335级钢筋，屈服强度实测值为435 N／mm2，混凝土强度等级为 C40，轴心抗压强度实测值为40.2 N／mm2。节点框架柱主轴方向正截面强度（按材料强度实测值计算）为144.5 kN·m（轴压比为0.2），实测柱梁强度比系数为1.3。试验于空间节点两主轴方向梁端同时加载，以模拟斜向45°方向加载，加载过程中框架柱上端施加恒定轴向压力（723 kN），梁端加载至节点发生破坏不能继续稳定承载而停止。根据试验数据得

等效截面正截面承载力 Meq可按式（10）计算，Meq轴向力 N在等效截面中对应的计算偏心距 e。其中可按式（11）计算Meq原截面正截面承载力仍满足式（8）的关系。到的框架柱斜向压弯强度实测值为129.3 kN·m，仅为框架柱主轴方向压弯强度实测值的89%。空间节点的破坏特征表明，主轴方向按照强柱弱梁设计的节点，斜向地震作用下框架柱因斜向（双向）压弯强度不足而发生破坏，是没有实现强柱弱梁的破坏机制的重要原因。

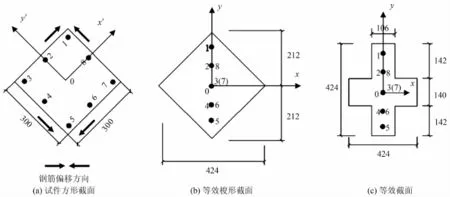
图4 试验试件等效截面图 ／mm

表1 截面几何参数

表2 钢筋坐标

根据试验45°方向加载条件，节点框架柱压弯作用平面应沿图4（a）中1号钢筋与5号钢筋连线方向，文中利用等效梭形法和简化计算方法分别对框架柱截面斜向（双向）压弯承载力进行计算，等效截面转换结果分别见图4（b）、（c）所示，截面几何尺寸转换计算结果及钢筋坐标转换结果分别见表 1 和2。通过对框架柱受力纵筋应变实测值的分析，认为达到破坏时角部钢筋均可进入屈服状态，故斜向（双向）压弯强度计算时对图4中1号和5号位置钢筋应力取屈服强度实测值，其它位置处钢筋应力可利用平截面假定确定其应变后代入本构方程计算得到。框架柱截面双向压弯承载力结算结果与试验实测结果的对比见表3。等效梭形法和文中简化计算方法所得结果与试验实测值符合均较好，且文章方法所得结果计算精度优于等效梭形法。

2.4 双向压弯构件正截面承载力提高方法

从以上分析可以看出，截面等效转换后受力纵筋均位于等效截面的中心对称轴上，其位置越靠近图3（a）中1号或5号位置，根据平截面假定其应变将会增大从而使得钢筋应力增大，这对提高截面的双向压弯承载力有利。文章在不改变原柱截面配筋数量和几何参数的基础上将图 3（a）中截面角部两侧边与1、5号钢筋相邻的纵向受力钢筋向角筋位置移动，如图3（a）中箭头所指方向，以加强截面角部配筋并对截面双向压弯承载力进行计算，计算结果见表4。计算时钢筋偏移距离考虑了2倍受力纵筋直径（32 mm）、4倍受力纵筋直径（64 mm）、与角筋紧密接触（偏移距离的极限情况）等3种情况。

表3 承载力计算结果

由表 4可知，随着纵向受力钢筋向角筋偏移距离的增大截面双向压弯承载力明显增加，提高幅度约为14%～42%。沿结构斜向的柱梁强度比随钢筋偏移距离的增大亦呈现出明显的增大趋势，这有利于结构在斜向（非主轴）方向地震作用下仍可实现“强柱弱梁”抗震设计目标并提高框架结构的抗震安全性。表4中斜向柱梁强度比为柱双向压弯承载力理论计算值与空间节点两主轴方向梁的实测抗弯强度沿45°加载方向合成结果（145.6 kN·m）的比值。

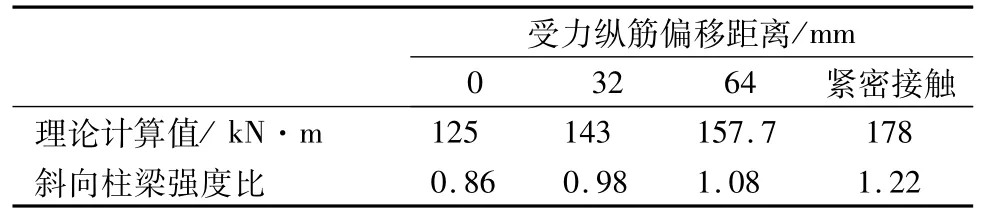
表4 加强配筋截面双向压弯承载力结果

3 结论

通过上述研究可知：

（1）框架柱双向压弯承载力仅为主轴方向正截面承载力的89%，双向压弯承载力不足是地震发生时框架柱破坏的原因之一。简化计算方法和等效梭形法得到的框架柱双向压弯承载力结果与试验实测值分别相差3%和5.5%，精度较好均可在实际工程中应用。

（2）截面纵筋向角筋偏移距离增大后框架柱双向压弯承载力明显提高，提高幅度约为 14%～42%。此外，空间节点沿斜向45°方向的强柱弱梁系数也逐渐增大，偏移距离为 4倍钢筋直径时该系数为1.08，可满足强柱弱梁抗震设计要求，有利于结构抗震。

（3）关于钢筋混凝土双向压弯构件正截面受弯承载力的计算方法，经过学者们的研究取得了一系列的成果，基于截面等效的方法是一种简化计算方法，能兼顾计算的正确性和使用的便捷性，可以为实际工程设计提供参考。但该方法对于一些特殊的截面形式（L形、十字形）适用性较差，仍然是一个需要继续研究的课题。

［1］ 杨红，张和平，骆文进，等.双向地震下 RC框架柱端弯矩增强措施的合理取值［J］.四川大学学报（工程科学版），2012，44 （1）：19－27.

［2］ 李英民，罗文文，韩军.钢筋混凝土框架结构强震破坏模式的控制［J］.土木工程学报，2013，46（5）：85－92.

［3］ 李振宝，李靖，宋坤，等.斜向地震作用下RC框架静动力弹塑性分析［J］.工程抗震与加固改造，2014，36（5）：1－7.

［4］ 杨红，孙永炜，张睿，等.基于梁铰机制的柱端弯矩增强措施研究［J］.土木工程学报，2014，47（4）：64－75.

［5］ 雷远德，曲哲，王涛.钢筋混凝土空间框架底层梁柱节点双向往复加载试验研究［J］.土木工程学报，2014，47（12）：64－73.

［6］ 杨红，徐云中，孙永炜，等.我国“强柱弱梁”措施表达式影响因素分析［J］.建筑结构，2015，45（12）：28－33.

［7］ 汪梦甫，邬文奇.塑性铰出现后钢筋混凝土框架柱的剪力重分配效应分析［J］.工程抗震与加固改造，2015，37（2）：1－8.

［8］ 陆婷婷，梁兴文.预期损失部位采用 FRC框架结构的屈服机制及抗震性能［J］.西安建筑科技大学学报（自然科学版），2016，48（1）：109－114.

［9］ 许卫晓，杨松伟，于德湖，等.多层钢筋混凝土框架结构抗地震倒塌研究进展［J］.青岛理工大学学报，2016，37（2）：1－7.

［10］Bresler B..Design criteria for reinforced columns under axial load and biaxial bending［J］.Journal of the American Concrete Institute，1960，32（5）：482－490.

［11］Alfred L..Capacity of reinforced rectangular columns subject to biaxial bending［J］.Journal of the American Concrete Institute，1967，63（9）：911－922.

［12］Fleming J.F..Design of columns subjected to biaxial bending［J］.Journal of the American Concrete Institute，1965，62（3）：327－341.

［13］ Tung A..Ultimate strength design of rectangular concrete members subject to unsymmertical bending［J］.Journal of the American Concrete Institute，1958，54（8）：657－674.

［14］杜宏彪.钢筋混凝土压弯构件在斜向周期反复荷载下的抗震性能［D］.北京：清华大学，1986.

［15］GB 50011—2010，混凝土结构设计规范［S］.北京：中国建筑工业出版社，2010.

［16］陈宗平，王妮，钟铭，等.型钢混凝土异形柱正截面承载力试验及有限元分析［J］.建筑结构学报，2013，34（10）：108－119.

［17］宋坤.钢筋混凝土柱斜向抗震性能及其加强方法研究［D］.北京：北京工业大学，2014.

［18］王伟，宋坤.钢筋混凝土受压构件正截面承载力的数值算法［J］.建筑科学，2014，30（5）：19－26.

［19］Mattock A.H..Rectangular concrete stress distribution in ultimate strength design［J］.Journal of the American Concrete Institute，1961，32（8）：875－928.

［20］鲍质孙.钢筋混凝土双向受弯构件的强度计算及其简化方法［J］.建筑结构学报，1984（1）.

［21］陈忠汉，朱伯龙，钮宏.斜向受力钢筋混凝土构件正截面强度计算［J］.同济大学学报，1984，（1）：90－100.

［22］刘春阳.斜向地震作用下RC空间节点破坏机理研究［D］.北京：北京工业大学，2011.

［23］张功新，何以农，虞锦晖，等.钢筋砼双向受弯构件抗剪强度的计算［J］.南昌大学学报，1997，19（3）：28－33.

［24］万鹏，虞锦晖，桂国庆.有腹筋预应力砼双向受弯构件抗剪强度的计算［J］.南昌大学学报，2000，22（2）：61－65.

［25］张立人.钢筋混凝土双向受弯构件强度与变形的试验研究及计算建议—— 负I形梁法［J］.建筑结构，1995，15（9）：3－7.

Simplified calculation of bending strength of biaxial compression-bending reinforced concrete column

Liu Chunyang，Wang Meng
（School of Civil Engineering，Shandong Jianzhu University，Jinan 250101，China）

Poor load carrying capacity of the reinforced concrete column under the biaxial compression-bending action is one of the reasons why the frame columns had been found damaged even collapsed during the earthquake.Without changing the section area，concrete compression zone area and the area moment to the neutral axis before and after the section equivalent conversion，based on the cross section equivalent method the equivalent section used for calculating the bearing capacity of the frame column under biaxial bending effect is found.Furthermore，the simplified calculation method on biaxial bending capacity of the frame column is established on the basis of equilibrium principle.The biaxial bending bearing capacity of the frame column of spatial joint is calculated by using the simplified method and the equivalent spindle section method.The calculation results and the experiment result show good agreement and the calculation accuracy of the simplified method is higher，the difference between them is only 3%.To improve the bearing capacity of biaxial bending section，the longitudinal steel bars are moved to the angle steel by 2，4times steel bar diameter and closely contacted with the angle steel bar，respectively.The reinforcement quantity and the cross section geometric parameters are unchanged.The calculation results show that the two-way bending bearing capacity is enhanced obviously by degree of 14%～42%，with the moving of the steel bars tothe angle steel.The research results could be good references to the practical engineering design works.

reinforced concrete column；biaxial compression-bending；bearing capacity；simplified calculation；equivalent cross-section

TU375

A

1673－7644（2016）05－0452－06

2016－07－03

山东省自然科学基金项目（ZR2015EQ017）；山东建筑大学博士科研基金项目（XNBS1202）

刘春阳（1980－），男，讲师，博士，主要从事工程抗震等方面的研究.E-mail：liucy2011＠sdjzu.edu.cn