短路匝式传感器干扰力矩分析

凌林本，赵新宇，刘晓东，王智奇，赵丙权

（天津航海仪器研究所，天津300131）

短路匝式传感器干扰力矩分析

凌林本，赵新宇，刘晓东，王智奇，赵丙权

（天津航海仪器研究所，天津300131）

短路匝式传感器带来的干扰力矩是引起陀螺仪随机漂移的重要因素之一，减小该项干扰力矩对提高陀螺精度能够起到重要的作用。本文利用电磁感应定律和磁路分析法对干扰力矩进行了推导，并通过Ansoft maxwell软件对短路匝传感器不同参数情况下的干扰力矩进行仿真分析，得出了转子转角、激磁电压和激磁频率对干扰力矩的影响关系曲线，最后合理选择参数以保证干扰力矩在精度允许范围内。该分析结果对减小短路匝传感器的干扰力矩和减小陀螺仪的随机漂移都具有一定参考价值。

短路匝传感器；随机漂移；干扰力矩；仿真分析

干扰力矩是引起陀螺随机漂移的主要因素，减小干扰力矩是提高陀螺精度的根本途径，而传感器的干扰力矩是诸多干扰力矩中的重要成分。短路匝式传感器的结构简单，不需输电装置，不存在导电游丝带来的弹性干扰力矩。但是，如果结构、参数不合理会产生较大的电磁干扰力矩，对陀螺精度产生较大影响。所以合理选择短路匝传感器参数，减小短路匝传感器的电磁干扰力矩，对提高陀螺仪精度有重要意义。

本文首先推导出了短路匝传感器干扰力矩的理论公式，得出影响干扰力矩的因素有转子转角、激磁电压和频率，然后将它们分别设为参数变量，利用Ansoft Maxwell对短路匝传感器的干扰力矩进行仿真分析，最后得出了干扰力矩的变化规律，为合理选择传感器参数提供了依据。

1 陀螺仪漂移误差

陀螺漂移误差[1]即漂移角速度，主要取决于其输出轴上所受到的干扰力矩，其静态漂移误差模型为

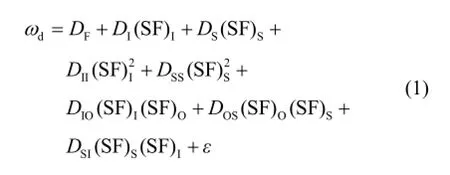
式中：dω为漂移角速度；FD为与角速度无关的漂移；DI、DS分别为IRA和SRA方向比力成正比的漂移参数；IID 为IRA方向比力平方成比例的漂移参数；SSD为与SRA方向过载平方成正比的漂移参数；IOD 、SOD为与IRA、SRA指定的两方向比力之积成正比的漂移参数；SID 为角动量轴方向比力平方成比例的漂移参数；ε为随机漂移角速度。对于每项漂移系数，都存在一个有规律的部分和一个随机变化的部分，我们应力求最大限度地降低它们。

在定性讨论了漂移系数的影响后，对其影响程度还需要一个定量的概念。对于一个角动量为 0.14 kg·m2/s的陀螺而言，要达到小于5×10-4(°)/h2的斜漂，干扰力矩的变化率必须小于2 nN·m/h。由于短路匝传感器没有弹性，干扰力矩只有电磁干扰力矩，所以短路匝传感器可以有效地减小传感器带来的干扰力矩。本文通过研究短路匝传感器干扰力矩的影响因素，合理地选择传感器参数使得干扰力矩达到最小。

2 短路匝传感器

短路匝传感器[2]如图 1所示。由外定子、导磁环和转子组成，外定子又包括定子铁芯、激磁线圈和输出线圈。定子磁芯和导磁环材料为锰锌铁氧体材料，短路匝为不导磁的良导体，安装在陀螺仪的框架轴上，可以在内、外定子间的气隙中自由转动。定子铁芯为八极结构，在相隔的磁极上分布有激磁线圈（Ⅰ, Ⅱ, Ⅲ,Ⅳ）和输出线圈（1, 2, 3, 4）。

各个激磁线圈和输出线圈串联起来。当传感器转子转过α角时，激磁磁通穿过短路匝转子与短路匝匝链间的磁通发生变化，短路匝转子内感应出电动势，从而形成短路电流。短路电流产生短路匝转子磁势，该磁势分别反作用于激磁线圈和输出线圈，使输出轴上的磁势分量与输出线圈匝链产生相互作用从而在输出线圈中感应出输出电动势。

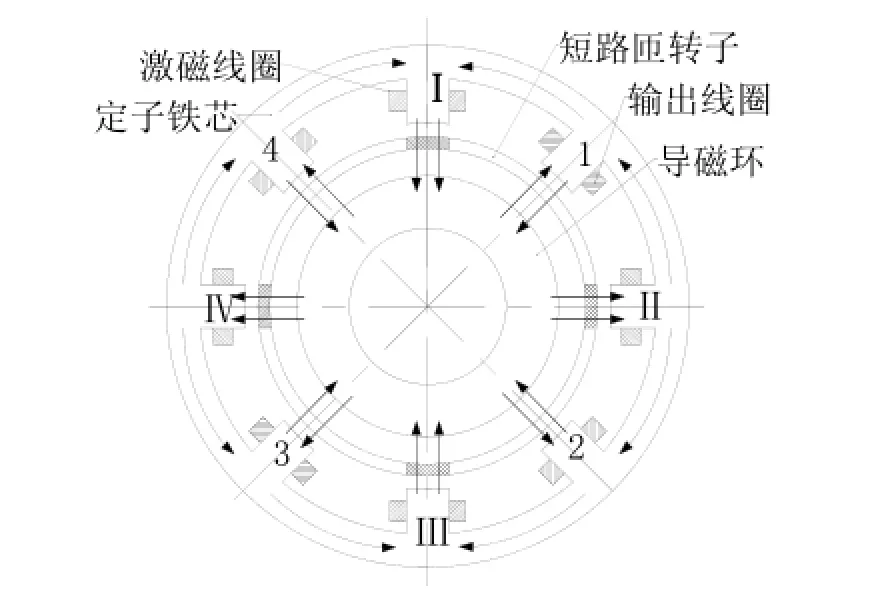
图1 短路匝传感器Fig.1 Shorted-turn sensor

3 短路匝传感器的输出特性

实际应用中陀螺仪表的传感器一般都接有容性负载，因此研究短路匝传感器在容性负载情下的输出特性[3]规律是十分有意义的。图2为传感器工作等效电路图。列出电路平衡方程式：

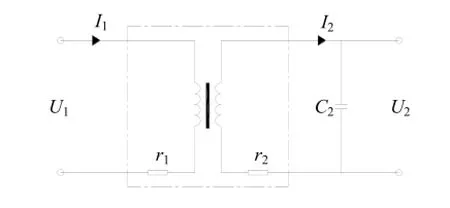
图2 短路匝传感器等效电路图Fig.2 Equivalent circuit of short-turn sensor

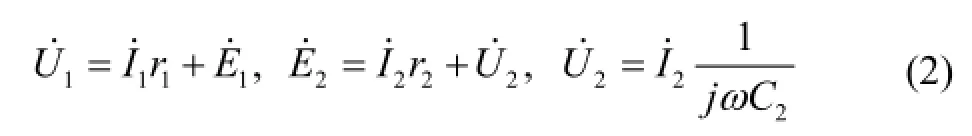
为了求传感器在容性负载情况下的输出特性，画出等值磁路图，如图3所示。

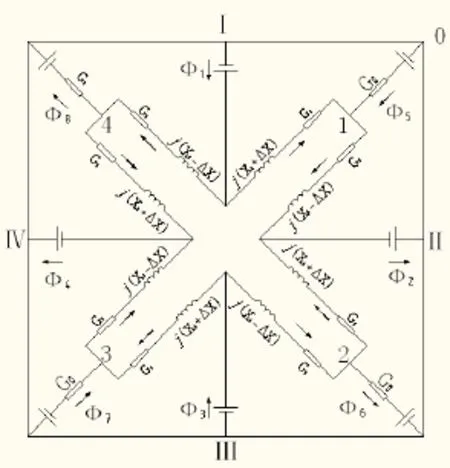
图3 短路匝传感器磁路图Fig.3 Magnetic circuit of shorted-turn sensor

式中：1W为激磁线圈的匝数；2W为输出线圈的匝数；X0为短路环等值磁抗的1 4； ΔX 为短路环转过α时磁抗的变化量； X kαΔ = ，k由激磁电压幅值、频率、材料以及传感器的外形结构决定；0G为单个磁极下主气隙磁导的1 2；为激磁磁通；为输出磁通；

根据节点磁位法以节点0为参考点，并令节点1、 2、3、4的磁位分别为列出节点1、2、3、4的磁势方程：

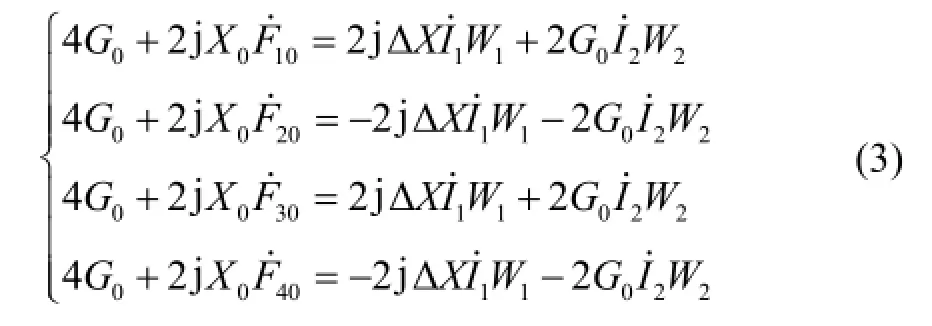
根据欧姆定律可以列出图3所示各个支路磁通方程：

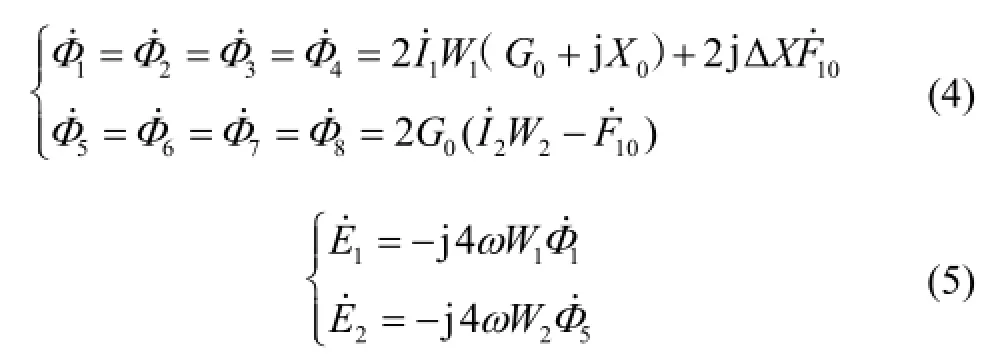
将式(3)(4)代入式(5)中得到1E˙、2E˙，将其带入式(2)中，并令：

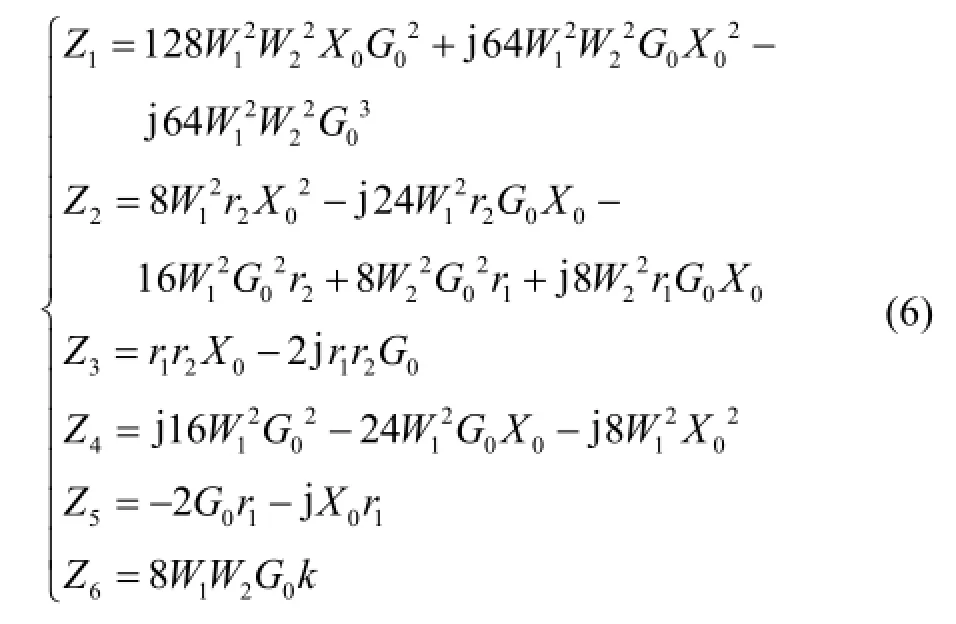
整理得：

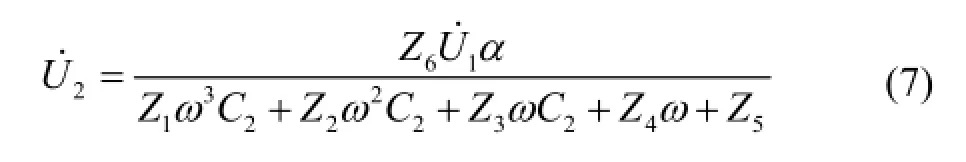
式中：α为短路匝传感器转子转过的角度；ω为激磁频率。

4 短路匝传感器的干扰力矩

短路匝式传感器产生干扰力矩的原因是转子中的电涡流力产生的力矩[4-7]。传感器检测电感线圈与被测体之间的相互作用可以认为是传感器检测电感线圈与涡流环线圈之间的相互作用。用1L便是检测线圈的电感，1r表示检测电感线圈的电阻；涡流环也有等效电感和等效电阻，分别为L和r；1M为1L和L之间的互感。图4所示即为电涡流传感器等效电路模型。

根据基尔霍夫定律KVL，上述等效电路可列出如下方程：

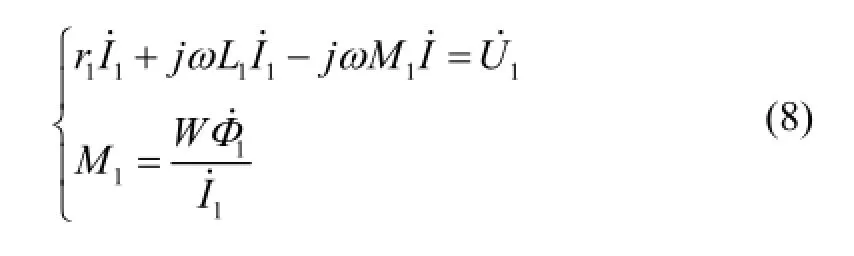
整理可得：

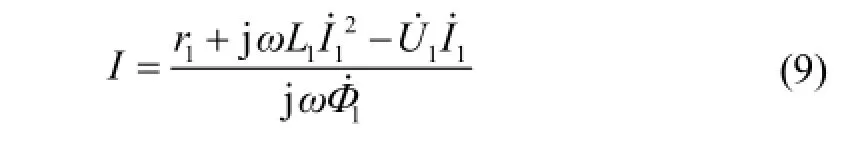
式中：1M为1L和L之间的互感系数；W为涡流环匝数；I为电涡流；1Φ˙为激磁磁通。

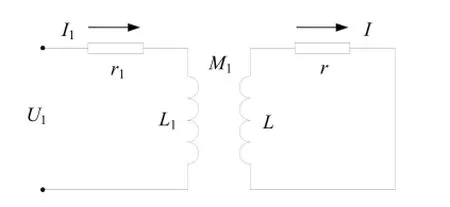
图4 电涡流模型Fig.4 Eddy current model

图5 为传感器转子转过α角的干扰力矩原理图，F为转子在磁场中所受的力。

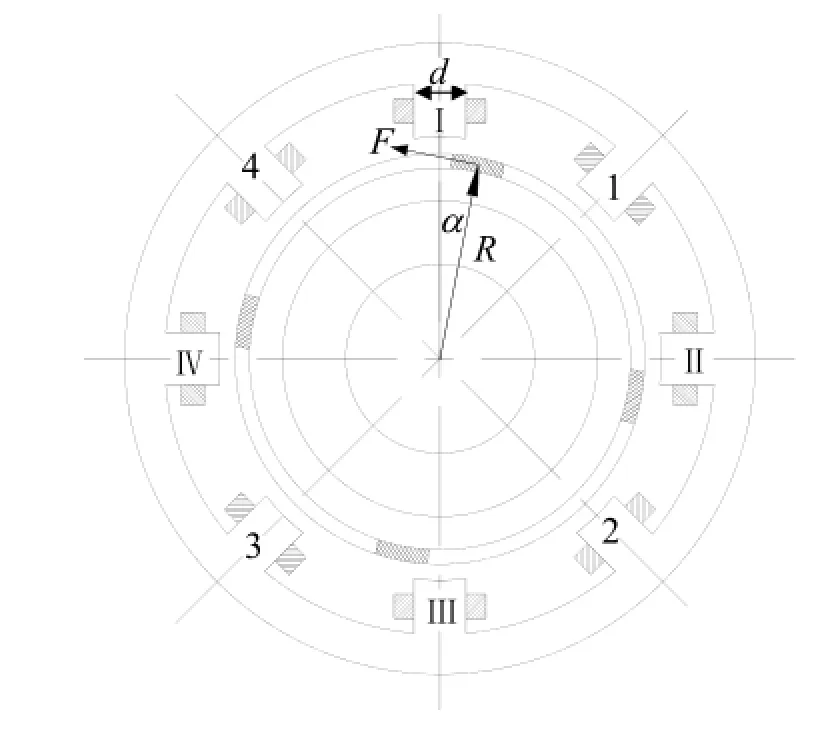
图5 干扰力矩原理图Fig.5 Disturbance torque diagram

根据图5可以写出干扰力矩方程：

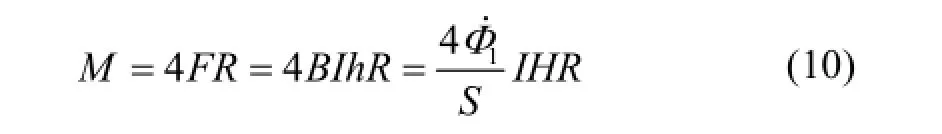
将式(4)(9)代入式(10)，并令：

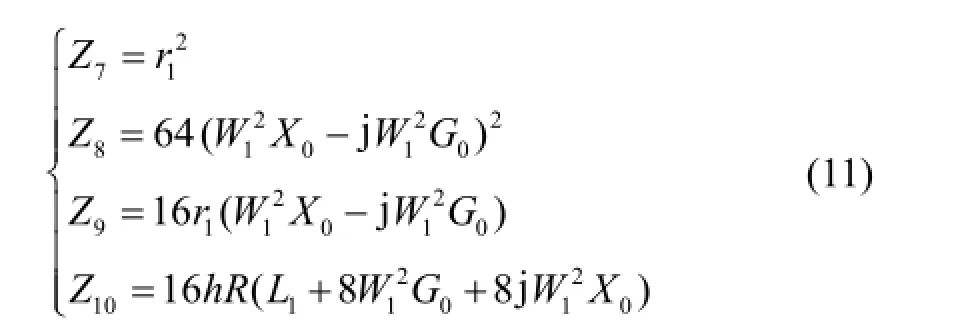
整理得：

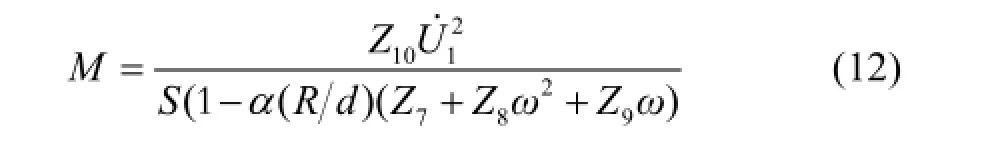
式中：M为干扰力矩；d为筋部宽度；S为激磁线圈面积；h为短路匝转子高度；R为短路匝转子半径。

由式(12)可以看出，在短路匝传感器基本尺寸确定的情况下，干扰力矩主要与激磁电压、激磁频率和转子转角等因素有关。

5 仿真分析

传感器磁场为激磁线圈产生的交流磁场，利用Maxwell 3D[8-10]对短路匝传感器的干扰力矩进行分析仿真，分析流程主要包括：Maxwell 3D实体建模→Maxwell 3D材料属性→Maxwell 3D的边界条件和激励源→Maxwell 3D的网格剖分和求解设置→数据后处理与结果分析。

5.1 实体建模和材料分配

三维短路匝传感器计算模型包括6个部分：定子铁芯、激磁线圈、输出线圈、转子、导磁环、空气求解域，分别对其进行建模。

在Maxwell自带的标准材料库基础上，建立传感器零件使用的材料库。定子铁芯、导磁环为铁氧体软磁材料，激磁线圈、输出线圈材料为纯铜。传感器的短路匝在磁回路中相当于一匝导电线圈，工作在高频激励磁场中，具有良好的导电特性，材料为LY12，其他区域为空气。

5.2 网格划分和求解器设置

在本文中，由于短路匝传感器模型尺寸较为规整，所以采用了手工剖分，如图6所示。

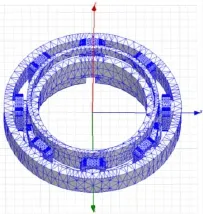
图6 短路匝传感器的网格划分Fig.6 Mesh of shorted-turn sensor

对三维短路匝传感器模型划分完网格后，还需要进一步检查所划分的网格质量。在检查质量之前，需要先设定求解器参数。质量之前，需要先设定求解器参数。在Analysis模块中设置仿真时间为5×10-4s，步长为2×10-6s；Sweep setup中起始时刻Start为0，终止时刻Stop为5×10-4s，间隔时刻Step为5×10-5s。

5.3 仿真结果

本来选用XX型号短路匝传感器作为研究对象，参量设置为力矩，对象为传感器转子，类型设为虚功力，绕Z轴顺时针为正方向。采用控制变量法，分别以转子转角、激磁电压和频率作为变量，利用Analysis模块对传感器的干扰力矩进行仿真计算。

5.3.1 干扰力矩与转子转角的关系

设置转子转角α为变量，角度为-5°～10°，其他数据取原始设计数据。用Analysis模块对力矩进行仿真分析，仿真结果如图7所示。

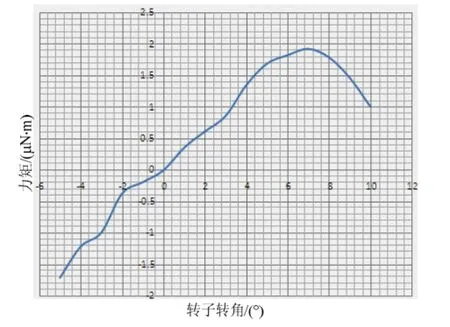
图7 干扰力矩与转角的曲线图Fig.7 Diagram of disturbance torque and angle

图7 所示是通过变化转子转角得到的传感器干扰力矩随转子转角关系。在-5°～5°间，干扰力矩基本随角度以0.34 μN·m/(°)呈线性变化。

5.3.2 干扰力矩与激磁电压、频率的关系

分别保持激磁频率不变，设置激磁电压 U1为参量，电压值为0～20 V；保持激磁电压不变，设置激磁频率f为参量，频率2～13 kHz；其他数据取原始设计数据。用Analysis/Setup3模块对干扰力矩进行仿真分析，仿真结果如图8、图9所示。

由仿真结果可以看出，干扰力矩与激磁电压平方成正比，与激磁频率成反比。

根据上述得到的干扰力矩随转子转角、激磁电压和频率的关系，合理地配置传感器参数。在选取工作角度为1°，激磁电压为8 V，激磁频率为8 kHz的情况下进行仿真，仿真结果如图10。

从图10中可以看出，在合理地选择参数之后，干扰力矩呈周期性变化，峰值变化率约为0.216 nN·m/h，此结果在高精度陀螺仪允许的干扰力矩控制范围内。

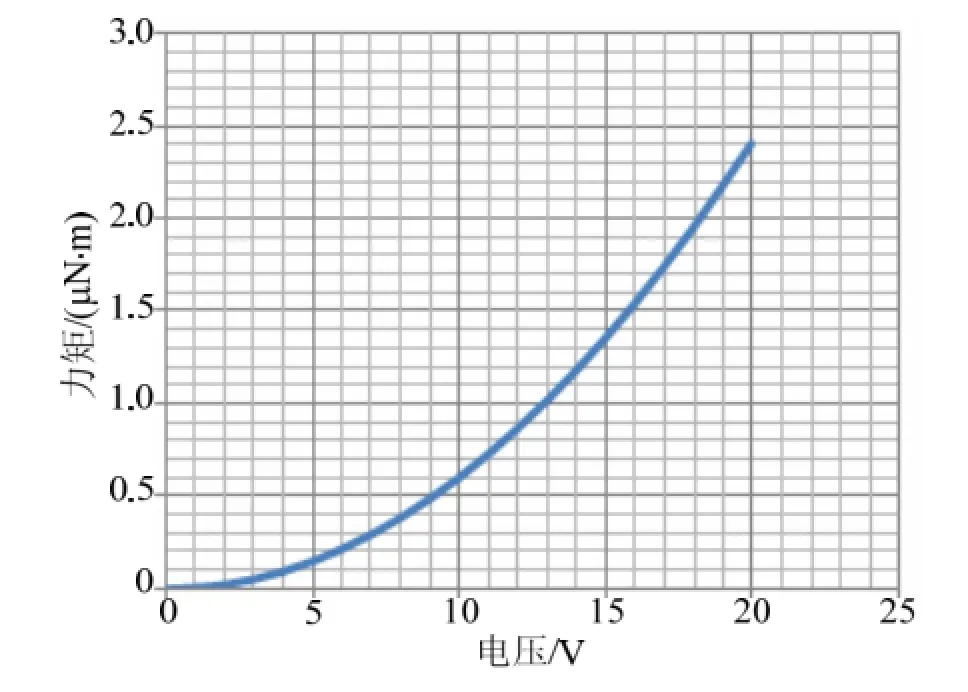
图8 干扰力矩与电压的曲线图Fig.8 Disturbance torque vs. voltage

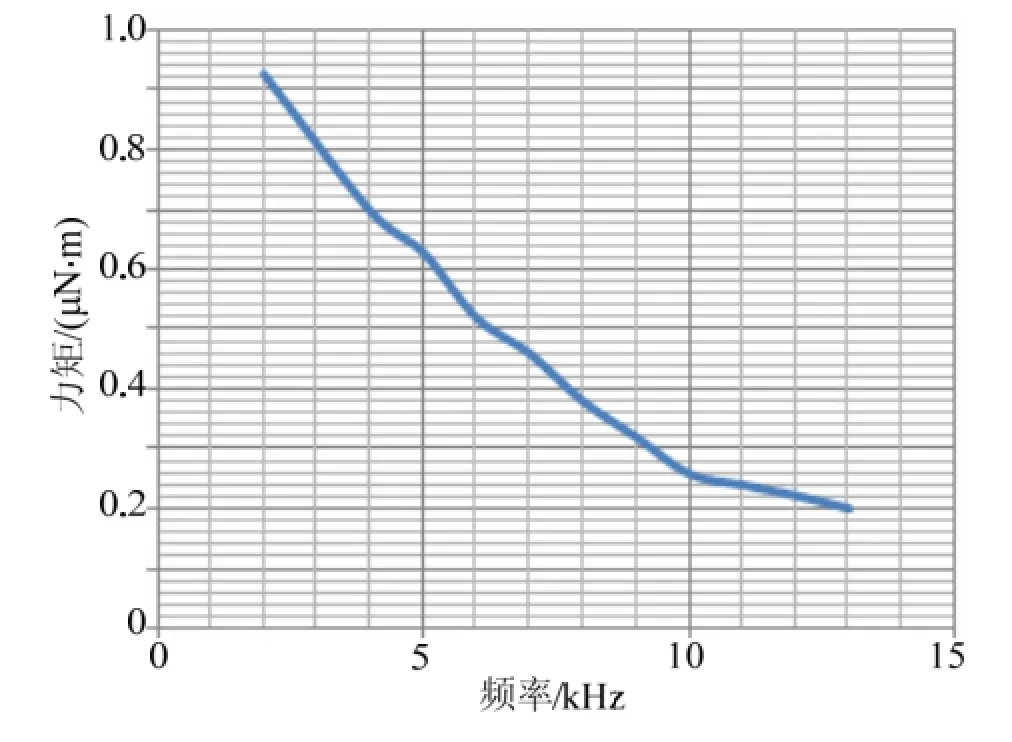
图9 干扰力矩与频率的曲线图Fig.9 Disturbance torque vs. frequency

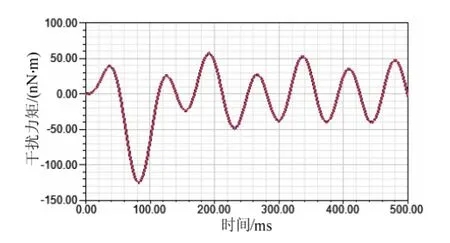
图10 干扰力矩的仿真结果Fig.10 Simulation result of disturbance torque

6 结 论

通过利用有限元分析软件Ansoft Maxwell对短路匝传感器的干扰力矩进行了仿真分析，分别对影响干扰力矩的几个因素进行参数设置，得出了干扰力矩与转子转角、激磁电压和频率之间的关系。在合理选择传感器参数后，得出干扰力矩仿真结果，为合理选择传感器参数提供了依据，对减小短路匝传感器的干扰力矩具有重要意义。

（References）：

[1] 陈桂明. 液浮陀螺仪性能改进技术[M]. 北京: 科学出版社, 2014.

Chen Gui-ming. Performance improvement of liquid floated gyroscope[M]. Beijing: Science Press, 2014.

[2] Rahman M A, Bakker M C. Sensor-based control in eddy current separation of incinerator bottom ash[J]. Waste Management, 2013, 33(6): 1418-1424.

[3] 吴畏, 聂鲁燕, 马利民, 等. Ansoft Maxwell电磁场分析在短路匝传感器输出特性中的应用[J].传感器与微系统, 2011, 30(6): 131-134.

Wu Wei, Nie Lu-yan, Ma Li-min, et al. The application of Ansoft Maxwell electromagnetic field analysis in the output characteristic of the short-turn sensor[J]. Sensor and Micro System, 2011, 30(6): 131-134.

[4] Chady T, Sikora R. Optimization of eddy-current sensor for multifrequency system[J]. IEEE Transactions on Magnetic, 2003, 39(3): 1313-1316.

[5] Zilberstein V, Schlicker D. MWM eddy current sensors for monitoring of crack initiation and growth during fatigue tests and in service[J]. International Journal of Fatigue, 2001, 23(3): S477-S485.

[6] Griesbach T, Wurz M C, Rissing L, et al. Development, fabrication, and test of a modular eddy current micro sensor on a flexible polymer foil[J]. Production Engineering, 2014, 7(1): 3-8.

[7] Kacprzak D, Taniguchi T, Nakamura K, et al. Novel eddy current testing sensor for the inspection of printed circuit boards[J]. IEEE Transactions on Magnetics, 2001, 37(4): 2010-2012.

[8] 赵博, 张洪亮. Ansoft12在工程磁场中的应用[M]. 北京: 中国水利水电出版社, 2010.

Zhao Bo, Zhang Hong-liang. Application of Ansoft12 in engineering field[M]. Beijing: China Water Power Press, 2010.

[9] 吴德利. 基于Maxwell 3D有限元分析的短路匝传感器输出特性研究[D]. 北京: 中国航天电子技术研究院, 2009.

Wu De-li. Study on the output characteristics of a shortturn sensor based Maxwell 3D finite element analysis[D]. Beijing: China Aerospace Electronics Technology Research Institute, 2009.

[10] 凌林本, 刘建社, 刘德均, 等. 液浮陀螺电磁场有限元分析[J]. 中国惯性技术学报, 2010, 18(2): 240-245.

Ling Lin-ben, Liu Jian-she, Liu De-jun, et al. Finite element analysis of electromagnetic field of liquid floated gyroscope[J]. Journal of Chinese Inertial Technology, 2010, 18(2): 240-245.

Disturbance torque analysis of short-turn sensor

LING Lin-ben, ZHAO Xin-yu, LIU Xiao-dong, WANG Zhi-qi, ZHAO Bing-quan
(Tianjin Navigation Instrument Research Institute, Tianjin 300131, China)

In view that the disturbance torque caused by the short-turn sensor may lead to the gyroscope’s random drift and hence reduce the gyroscope’s accuracy, the disturbance torque was deduced by using an electromagnetic induction law and magnetic circuit analyses, and the simulations for the disturbance torque with different sensor parameters were made by using Ansoft Maxwell. The influences of angle, voltage and frequency on the disturbance torque were obtained, and reasonable parameters are chosen to guarantee the disturbance torque be within the allowed error range. The analysis results provide a certain reference for reducing the disturbance torque of the shorted-turn sensor and hence the random drift of the gyroscope.

short-turn sensor; random drift; disturbance torque; simulation analysis

U666.1

A

1005-6734(2016)01-0083-05

10.13695/j.cnki.12-1222/o3.2016.01.015

2015-09-17；

2015-12-14

凌林本（1964—），男，研究员，研究生导师，研究方向为精密仪器与仪表。E-mail: ling_linben8@163.com