直线、射线、线段教案

陈正意

一、教材分析

1、教材的地位和作用

直线、射线、线段是学生在感受了多姿多彩的图形之后正式接触的几何基本图形，其探究的主要内容是直线的性质、线段的画法、比较及其性质。直线、射线和线段不仅是构成现实世界的基本元素，而且其相关概念、性质、表示法、画法也是几何学习的基础。教材充分利用了现实世界的实物原型，让学生直观感受，通过“观察”、“思考”、“探究”这些活动来鼓励学生勤思考、勤动手、多交流，从而转变学生的学习方式，并在此过程中渗透应用数学的意识。充分体现了以人为本的教育体念，有助于培养学生的探究意识和创新精神。

2、重、难点分析

由于直线的性质是几何研究的基础公理，所以本节的教学重点为：探索直线的性质；由于学生刚开始接触几何，对于几何图形的表示方法及几何语言的理解都存在一定的困难， 所以本节的难点为：几何图形的表示及几何语言的理解。

二、目标分析

根据课程标准，结合学生的年龄特点和认知结构，从知识与技能、过程与方法、情感态度与价值观三个维度确定了本节的教学目标如下：

知识与技能目标：

1、体会两点确定一条直线。

2、理解直线、射线和线段的概念信它们的区别和联系。

3、理解简单的几何语言，能根据几何图形说出其几何意义。

过程与方法目标：让学生经历观察、画图、交流等活动过程积累活动经验，建立初步的空间观念，发展形象思维。

情感态度与价值观目标：1、通过数学活动初步认识数学与人类生活的密切联系，增强学生对数学的好奇心与求知欲

2、通过学习几何图形的表示法及几何语言，培养学生严谨的科学态度

三、教学过程

（一）创设情景，引入课题。

让学生感受一组画面，观察并找出自己熟悉的图形，从而引出本节课题：直线、射线、线段。

（二）建立数学模型，探索新知识。

1、提出问题

要在墙上固定一根木条，至少需要几个钉子？

（1）分组动手操作并讨论。

（2）讨论结论：至少需要两个钉子可以固定一根木条。

2、建立模型

（1）画图①经过一点O画直线，能画几条？②经过两点A、B呢？

（2）让学生充分发表自己的看法，让各组选一代表发言。

3、模型解释

（1）通过实验和探究，归纳得到：

①经过一点有无数条直线

②经过两点有一条直线，并且只有一条直线

（2）教师解释：①中“直线经过一点”和②中“只有“的意思。

4、模型应用

让学生用所学知识解释

①木工师傅锯板用墨线弹出一条直线。

②栽电杆时，只要定出两根电杆便可把电杆栽在一直线上。

说明：教师对学生的回答要及时、恰当的给予肯定。

5、表示法

由于两点确定一条直线，因此我们经常用直线上的两个点来表示这条直线。

（1）直线的表示方法：①用直线上的任意两点表示，两点用大写字母，如直线AB或直线BA；②用一个小写字母表示，如直线a。

（2）通过多媒体把直线变化成线段，得到线段的表示方法：①用线段的两个端点表示，如线段AB或线段BA；②用一个小写字母表示，如线段a。

（3）通过多媒体把直线变化成射线，得到射线的表示方法：①用射线的端点和射线上的另一个点来表示，注意强调表示端点的字母应放在前面，如射线AB；②用一个小写字母表示，如射线L。

（三）初步运用。

如图，判断下列说法正误。

（1）直线、射线、线段都有两个端点。

（2）直线和射线可以延伸，线段不能延伸。

（3）直线AB和直线AC表示的不是同一条直线。

（4）线段BC和线段CB表示的是同一条线段。

（5）射线AC和射线CA表示的不是同一条射线。

巩固理解：

指出：对于第（5）小题，由于端点和方向不同，所以它们不是同一条射线。

（四）深化练习，培养能力。

1、探究

怎样由一条线段得到一条射线或一条直线呢？

（1）学生画图、讨论、交流。

（2）引导学生用语言表述：把线段向两方中任意一方延长，可以得到一条射线，把线段向两方延长，可以得到一条直线。

2、综合练习：

①画一条直线a经过点A、B

②过直线外一点C画直线b与直线a相交于点B

③画线段AC

④延长线段AC和反向延长线段AC

指出：延长线段AC和反向延长线段AC的区别。

⑤变式练习：

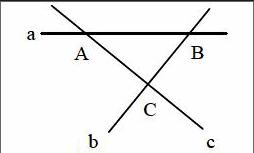
如图，用语言来描述几何图形：

①点A、B、C与直线a分别有什么位置关系？

②直线a，b是什么位置关系？直线b，c， 直线c，a呢？

（2）对于①教师指出：点和直线有

两种位置关系，点在直线上和点在直线外，对于②指出：直线a，b相交于A，也就是说A既在直线a上也在直线b上，即点A是直线a，b的公共点。

（3）小结：这个图形也可表述为：三条直线a，b，c两两相交，交点分别为A，B，C。

（五）应用延伸，发展思维。

1、应用延伸：

应用：从崇阳到武汉的公路线，有白霓、路口、温泉、咸安四个站，已知每两站间的票价不同，请问有多少种票价？

延伸：直线上有5个点时，共有多少条线段？有10个点呢？

2、探究思考

两条直线相交有一个交点，那么三条直线相交最多有几个交点呢？四条直线呢？你能找到规律吗？

（1）以小组为单位画图和讨论。

（2）通过动画演示启发学生得到规律，并思考：n条直线相交时，最多有多少个交点？

（六）归纳小结，整理反思。

两个思想：模型化思想和分类思想。

（七）作业：

1、课后习题。

2、观察生活，列举应用直线性质的实例。

四、教学反思

本节课的教学设计，体现三个注重：

1、注重学生对几何学习兴趣的培养。

2、注重对“基础知识”、“基本技能”的理解，掌握和创新能力的培养。

3、注重师生间的互动与交流。