恒温水箱控制系统参数整定算法的研究

李国林，朱林涛

(中国电子科技集团公司第四十五研究所，北京100176)



恒温水箱控制系统参数整定算法的研究

李国林，朱林涛

(中国电子科技集团公司第四十五研究所，北京100176)

摘要：恒温水箱的性能在很大程度上取决于对温度的控制性能，而系统整定参数的好坏又决定了其控制效果，因此，如何找到最优的整定参数显得尤为重要。为此，提出了一种针对恒温水箱的基于阶跃响应法的PID参数整定算法，并设计了以单片机为控制器的温度控制系统，且对该参数整定方法给以实验验证，得到了很好的控制效果。

关键词：恒温水箱；PID参数；整定算法；温度控制；单片机

随着计算机控制技术的发展，恒温控制己在工业生产领域中得到了广泛应用，并取得了巨大的经济效益。在不同的领域内，由于控制环境、目标、成本等因素的不同，需要针对具体情况来设计控制系统结构和功能，从而取得最佳的控制效果。其中，恒温环境的自动化控制技术是工业生产中的一个重要的研究领域。

由于水的比热比较大，且来源广泛，而且水加热到沸点时温度就不会再升高，因此我们常用水作为恒温控制的对象，从而产生了恒温水箱的广泛应用。比如，恒温水箱可供医疗单位、院校、科研、化工、印染等行业的化验部门做蒸馏、干燥、浓缩及恒温加热化学药品及生物用品恒温培养，以及对器械进行煮沸消毒之用等。而恒温水箱的性能很大程度上取决于对其水温控制效果的好坏。

本文首先简述了PID控制器的基本原理，重点介绍了基于阶跃响应法的PID参数整定算法的基本原理，并以单片机为控制平台设计了水箱控制系统，利用温度传感器采集温度，通过设定温度值与采集温度值的大小比较来控制固态继电器的通断，实现对被控对象水的温度控制，并得到了较好的实验控制效果。

1　PID控制器的基本原理

常规的PID控制系统的框图如图1所示，该系统主要由PID控制器和被控对象组成。作为一种线性控制器，它根据设定值r(t)和实际输出值y(t)之间形成控制偏差e(t)，并将偏差按比例、积分和微分作用通过线性组合求出控制量u(t)，从而实现对被控对象的输出控制。

PID控制器根据给定值和实际输出值构成控制偏差，即：偏差e(t) = r(t) - y(t)，则PID控制器的时域微分方程为：

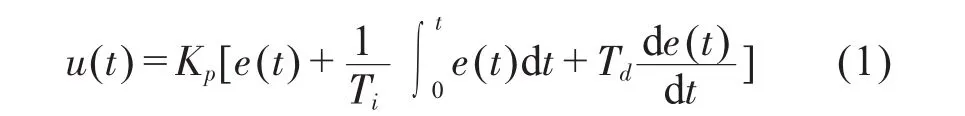
其中，Kp为比例系数，Ti为积分时间常数，Td为微分时间常数。

其中，比例增益的引入是为了及时地反映控制系统的偏差信号，一旦系统出现了偏差，比例环节立即产生调节作用，使系统偏差快速向减小的趋势变化。积分作用的引入是为了消除系统的稳态误差，提高系统的无差度，以保证实现对设定值的无静差跟踪。微分作用的引入，主要是为了改善控制系统的响应速度和稳定性。微分作用能反映系统偏差的变化律，预见偏差变化的趋势，因此能产生超前的控制作用。

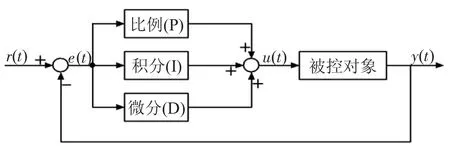
图1　PID控制系统原理框图

2　基于阶跃响应法的PID参数整定算法

在绝大多数的工业过程控制中，虽然被控对象往往具有非线性、时变等特点，但在具体的控制系统设计时，往往可以使用一阶惯性加纯滞后模型来近似或等效表示，其被控对象的传递函数模型为：

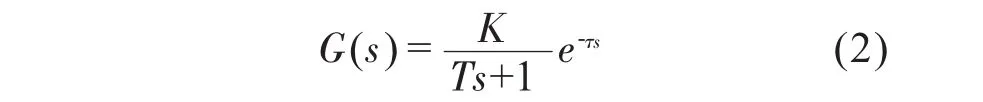
其中，K、τ、T分别为对象模型的开环增益、纯滞后时间系数和惯性时间常数。

假设系统的阶跃输入的变化量为△U，那么它的拉氏变换为U(s) =△U/s，根据传递函数的定义，输出的拉氏变换为Y(s)=G(s)·U(s)。

根据拉氏变换的终值定理，则有：

则可求得此被控对象模型的开环增益为：

其中，y∞为阶跃响应曲线的稳态值，也就是输出的最终值。

一阶惯性加纯滞后环节的阶跃响应曲线是一条负指数规律上升的曲线，即：

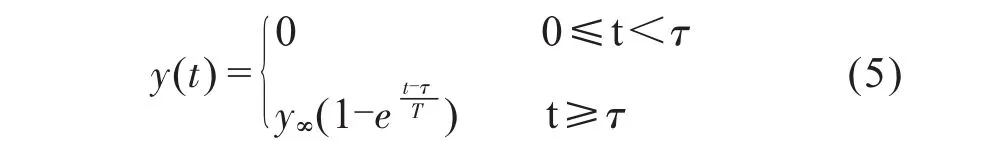
其中，T、τ分别为被控对象模型的惯性时间常数和纯滞后时间系数。

实际辨识过程中，阶跃响应不一定正好具有负指数规律上升的曲线，只要类似图2所示的S型非周期曲线，就可用一阶惯性加纯滞后环节的传递函数来近似，其中主要有两种方法——切线法和两点法。

实际应用中，由于切线法很难准确地确定最大切线斜率点，因此，一般采用两点法来近似系统的一阶传递函数，如图2所示，在曲线y(t)上选取两个坐标点(t1，y(t1))和(t2，y(t2))，只要0，y(t1)，y(t2)三个值之间有明显的差异即可。

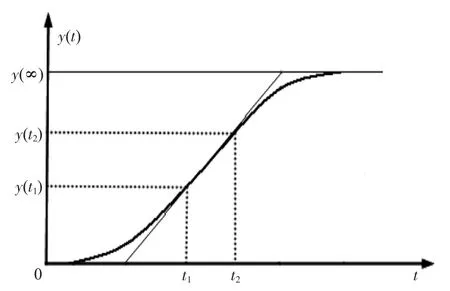
图2　阶跃响应曲线

将上述两点坐标分别代入式(5)中整理，并将式中y(t1)，y(t2)分别记为Y1，Y2。则可求得：

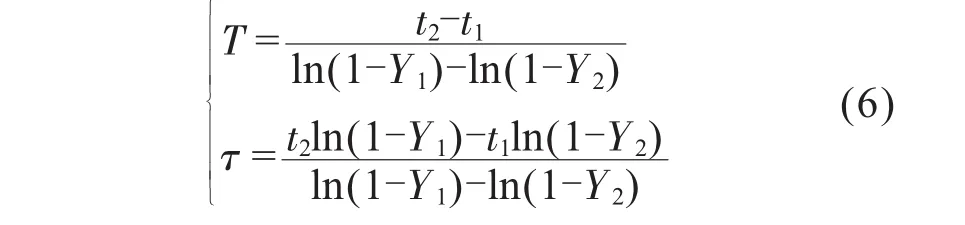
为了实际应用方便，可以选择y(t1) = 0.284和y(t2) = 0.632这两个固定值，那么可将τ和T整理为：

再根据Ziegler-Nichols经验公式结合上述参数(K、τ、T)从而可求得PID控制器的三个参数分别为：

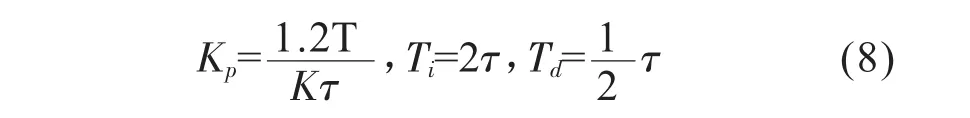
图3为一给定输入变化量为△u的阶跃响应曲线。

则，模型的开环增益可表示为：

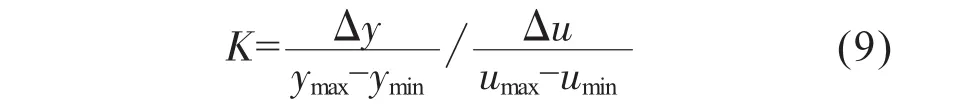
其中，umax、umin分别是控制量输出的最大值和最小值，ymax、ymin分别是被控对象输出量的最大值和最小值，而△u和△y分别为输入变化量和输出变化量。

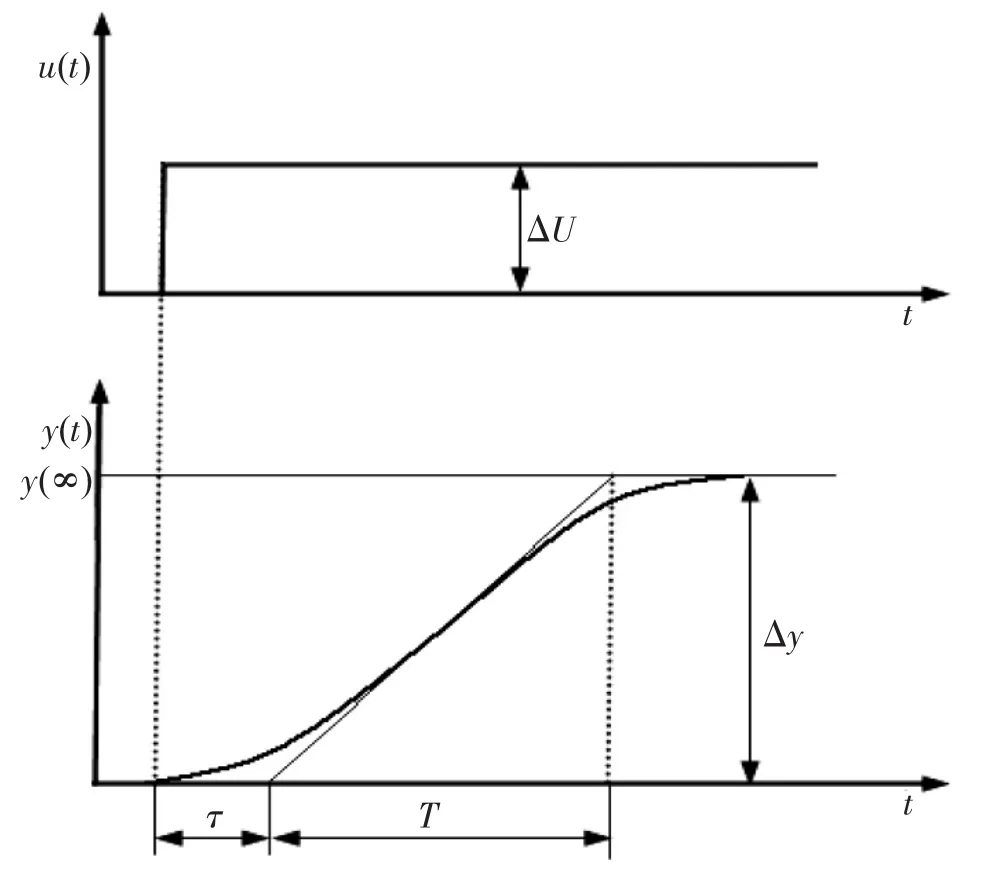
图3　给定输入的阶跃响应

给被控对象一个全功率加热的阶跃响应，设定被控对象从0℃经过滞后时间t0开始，并以相同的斜率k升温，且最后达到一个稳态值y∞（这里y∞取值100，也就是水在标准大气压下的沸点），从而可以求得被控对象模型的开环增益为K = 1，则可以根据滞后时间t0和升温斜率k求出t0.284和t0.632为：

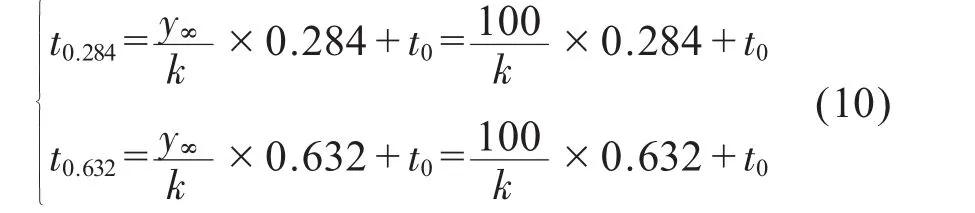
其中，t0.284和t0.632分别表示温度到达0.284△y 和0.632△y时所对应的时间。然后再根据式(6)、(7)和(8)求得PID控制器的三个参数Kp、Ti和Td。

3　恒温水箱控制系统的设计与实验

本文所设计的控制系统恒温水箱控制系统主要由六部分组成：CPU（单片机）主控制模块、电源模块、键盘输入模块、温度采集模块、继电器控制模块及LED显示模块。CPU主控制模块采用AT89C51芯片，把数字温度传感器采集到的温度信号与原预先设定值进行比较，然后根据其差值通过PID调节整定，控制继电器的通断进行不同加热方式，并且具有键盘输入温度给定值、定时时间，LED数码管显示温度值、时间和定时报警的功能，实现了自动控制温度的目的。

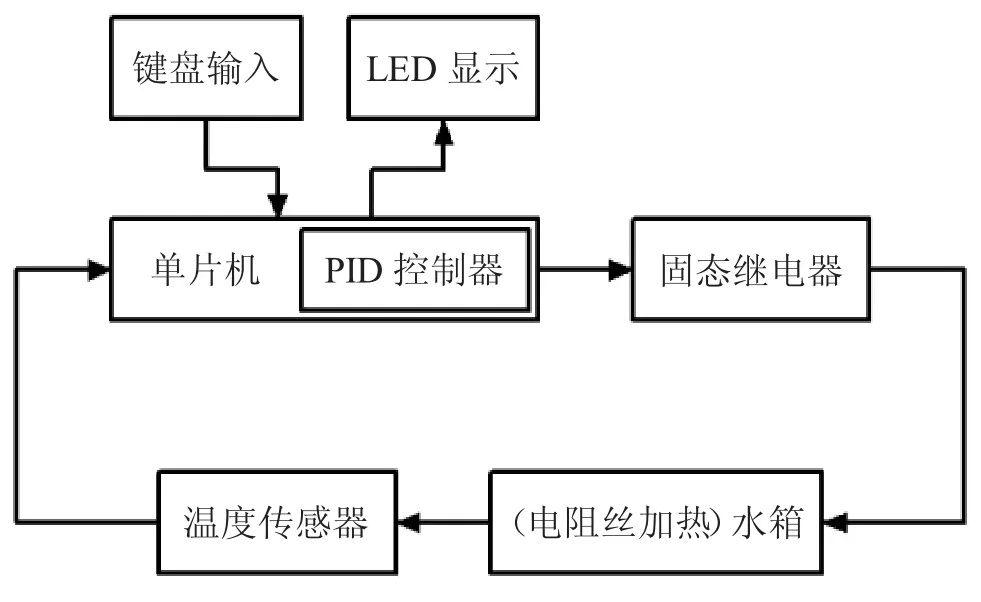
图4　恒温水箱控制系统框图

本系统是采用闭环负反馈的控制方式进行控制的，它通过数字温度传感器检测水箱内的水温温度，把采集到的数据直接送到单片机进行处理，由于数字式温度传感器能在极短时间内把采集到的模拟量转换成数字量，这样被它处理的数据直接送到数字PID控制器模块进行调整和控制PWM波形的产生。然后，把检测到的数据与预先设定的温度值进行比较，根据不同的差值去控制固态继电器的通断，从而达到控制被控对象温度的目的。另外，还设置了温度实时显示的装置，可以同时显示预先设定的温度值和实际检测到的温度值。

水温控制过程主程序流程如图5所示，采集温度值PV与设定温度值SP进行比较，当PV〈0.632 (SP- y0)时，其中y0是水箱中水的初始温度值，控制器对被控对象输出加热，当PV〈0.632(SP- y0)时，根据参数整定原理求出相应的P、I、D三个参数，而当PV〈0.632 (SP- y0)时，开始对被控对象进行PID控制输出过程，并根据实时温度值与设定值的比较求出输出控制量，并转化成输出占空比来控制固态继电器的通断，从而实现对被控对象的稳定控制。

水温控制过程还采用了不完全微分和变速积分相结合的PID控制算法，实验结果如图6所示，可以看出控制效果较好。

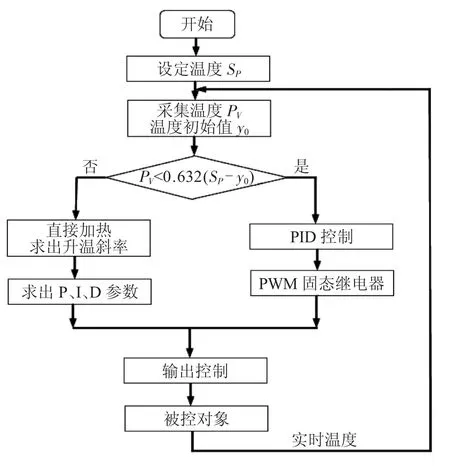
图5　主程序控制流程图

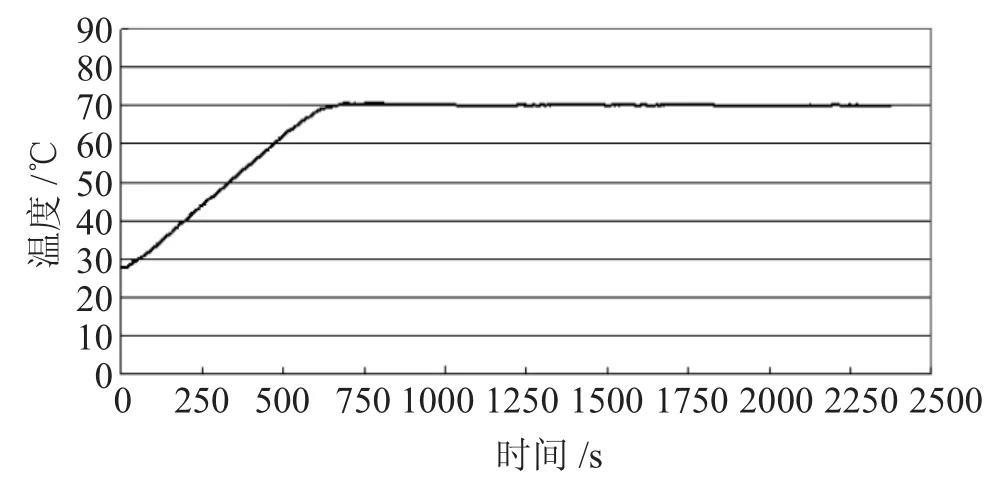
图6　在70℃的恒温水箱温度控制曲线

4　结　论

本文主要介绍了基于阶跃响应法的PID参数整定算法并给出了相应的恒温水箱硬件系统设计方案以及相应的实验结果，可以看出，文中的这种参数整定算法是专门针对被控对象为水的恒温水箱提出的，它不但可以很快地整定出控制器参数，还解决了传统控制中PID参数不易整定的缺点，有效地减小了被控对象的超调量，提高了控制系统的控制精度。通过大量的实验验证了此PID参数整定算法的可行性，此方法应具有很强的实际应用价值。

参考文献：

[1]陶永华.新型PID控制及其应用[M].北京：机械工业出版社，2002.

[2]刘金琨.先进PID控制MATLAB仿真[M].第3版.北京：电子工业出版社，2011.

[3]胡寿松.自动控制原理[M].北京：科学出版社，2001.

[4]吴炳胜.王桂梅. 80C51单片机原理与应用[M].北京：冶金工业出版社2001.

[5]耿长清.单片机应用技术[M].北京：化学工业出版社. 2002.

[6]李全利.单片机原理及应用技术[M].第3版.北京：高等教育出版社，2008.

[7]候玉宝. 51系列单片机设计与仿真[M].北京：电子工业出版社，2008.

[8]李群芳.单片机微型计算机与接口技术[M].北京：电子工业出版社，2007.

[9]陈富安.单片机与可编程应用技术[M].北京：电子工业出版社，2003.

[10]张卫东. PID控制器自整定技术的发展[R]. 2002年世界控制大会总结报告. 2002.

[11] J. G. Ziegler，N. B. Nichols. Optimum Settings for Automatic Controllers[J]. Trans. ASME，1942，64：759-768.

[12]王伟，张晶涛，柴天佑. PID参数先进整定方法综述[J].自动化学报. 2000，(3)：347-355.

[13]王伟，张晶涛，潘学军.基于偏置继电反馈辨识的改进自整定PID控制器[C].中国控制会议论文集. 2001，辽宁大连.

[14]李国林. PID控制器参数整定技术研究与优化设计[D].大连：大连理工大学硕士学位论文，2010．

[15]胡晚霞，余玲玲. PID控制器参数快速整定的新方法[J].工业仪表与自动化装置，1996，(5)：11-16.

[16]谢元旦，夏淑艳. PID调节器的继电自整定方法[J].控制与决策，1993，8(1)：77-80.

李国林（1985-），男，山东人，硕士研究生，工程师，现在中国电子科技集团公司第四十五研究所主要从事电子专用设备的研发与设计工作。

The Thermostat Tank Control System Parameter Tuning Algorithm

LI Guolin，ZHU Lintao
(The 45th Research Institute of CETC，Beijing 100176，China)

Abstract:The performance of the constant temperature water tank temperature control performance depends largely on the quality of system tuning parameters and its control effect，therefore，how to find the optimal tuning parameters is particularly important. A constant temperature water tank tuning PID parameters based on the step response method algorithm is proposed and designed the chip as controller temperature control system，and experimental validation of the parameter tuning method give good control effect.

Keywords:Constant temperature water tank；PID parameters；Tuning algorithm；Temperature control；Micro-controller

作者简介：

收稿日期：2016-01-29

中图分类号：TN668

文献标识码：B

文章编号：1004-4507(2016)04-005105