航空兵协同对海打击时间协同模型研究

马海洋，李　冬，孙怀亮(. 海军航空工程学院，山东　烟台，6400；. 黄海水产研究所，山东　青岛，66000)



航空兵协同对海打击时间协同模型研究

马海洋1，李冬1，孙怀亮2
(1. 海军航空工程学院，山东烟台，264001；2. 黄海水产研究所，山东青岛，266000)

摘要:时间因素在协同作战中作用日益凸显。首先对简单时间约束网络进行了分析，而后根据时间约束网络，对航空兵协同时间约束进行了定量化，将定量时间约束转化为 STCN 要求的不等式形式，给出了时间协同STCN 模型建模的具体流程，最后，建立了基于 STCN 的 d 个协同动作时间约束模型。

关键词：航空兵；协同动作；TCN；时间约束模型

0　引　言

随着现代战场的日趋复杂，协同作战已经是当前航空兵对海作战的基本作战方式。其中，时间在协同作战中，已经作为一个不可忽视的因素，得到越来越多重视。时间协同不利将可能导致任务失败乃至战场失利的严重后果。

航空兵对海打击协同作战过程中，根据火力和空间协同要求，以及各编组作战能力和训练情况等得出各协同动作持续时间和间隔时间要求，确定各协同动作的结束时间和开始时间，得到初始时间协同计划。但由于指挥员及参谋人员认知水平的局限性，初始计划中可能存在潜在的、隐性的时间约束冲突，导致时间协同计划无法实施，影响作战行动顺利实施和展开。因此，需建立协同动作间的时间协同模型，用来进行合理的时间协同安排。

1　协同时间约束关系描述

将航空兵对海打击协同作战过程中，航空兵不同

编组不同阶段的作战行动进行分解，得到协同动作集

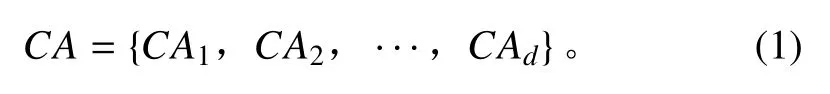
其中 CAd为第 d 个协同动作。协同动作之间的约束包括时间约束和功能约束[1-2]。航空兵编组间的协同动作可表示为一个时间约束动作组（CA，TC），其中TC 表示协同动作的时间约束。

借助时间点约束和时间区间约束，以及时间变量之间的定性约束和定量约束，以及时间约束关系的转换方法，可全面描述航空兵协同对海打击过程中编组协同动作之间的时间关系。

基于以上研究，航空兵编组协同动作的时间约束TC 可用如(2)式所示的一个四元组来描述。

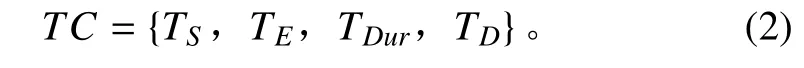
其中，协同动作自身时间描述包括三个参数：开始时间 TS、结束时间 TE以及至少持续时间 TDur。协同动作之间的时间描述为最小间隔时间 TD。而且 TDur、TD可转化为等效的时间点约束形式。

2　简单时间约束网络

TCN 不仅能够形象准确地表达许多实际问题和系统，而且通过相关的算法能够支持对时间的推理，如检测系统内各个活动时间约束的一致性等。目前己经在许多规划和调度系统中得到了较为广泛应用[3-5]。

基于协同动作的时间约束关系和描述方法，下面研究简单时间约束网络的相关概念、理论和模型。为建立航空兵协同对海打击的时间协同模型奠定理论基础。

首先给出时间约束满足问题（Temporal Constraint Satisfaction Problem, TCSP）的定义。

定义1 TSCP：TCSP 为一组变量集

和一组作用于该变量集上的约束集

变量集 VA 中的每个元素代表一个时间点，而约束集合C 中的每个元素表示时间点之间的时间约束关系。

当赋值

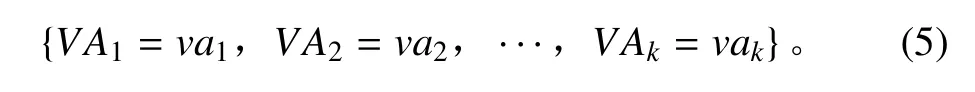
满足所有变量之间的时间约束关系时，则称元组

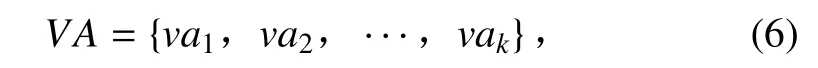
为时间约束满足问题的解。

由于 TCN 能够有效地描述 TCSP，并对 TCSP 中的约束集进行快速的推理。因此，TCN 是求解 TCSP 的一种非常方便、快捷的模型。TCN 定义如下。

定义2 TCN：TCN 是 TCSP 的图论描述形式，每个TCN 表示为一个有向约束图

其中顶点集 V 表示时间点集合 VA，边集 E 对应时间约束集合 C。

对于 G 中的任一条边 Eij，其对应的两个时间点VAi，VAj，满足约束

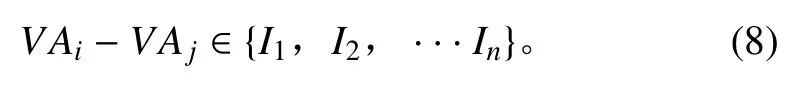
即，2 个时间点 VAi、VAj在时间轴上的距离VAj−VAi必须落在 {I1,I2,···,In} 某一区间范围内。若某约束条件为一元约束，可按前述方法转化成二元约束。下文统称一元约束、二元约束为约束区间。

建立 TCN 之后，TCSP 的求解就转化为了 TCN 的一致性检测问题。对于一般的 TCSP，如果作用于一对变量的约束区间有多个，且约束区间是连续时，计算其一致性的时间复杂度与每对变量的约束区间数呈指数关系增加，给求解带来很大困难。而当作用于每一对变量的约束区间只有一个时，其求解将不存在该问题。因此，在求解时，往往将其转化为简单时间约束满足问题。

下面参照定义给出简单时间约束满足问题（Simple Temporal Constraint Satisfaction Problem, STCSP）的定义。

定义3 STCSP：在一个 TCSP 中，当作用于所有变量对的约束皆为单一约束区间时，则称该 TCSP 为STCSP。

参照定义，给出简单时间约束网络（Simple Temporal Constraint Network, STCN）的定义。

定义4 STCN：若作用于有向约束图G 中每条边的约束都是单一约束区间时，则称 G 表示的 TCN 为STCN。不妨将其图论描述形式称为距离图。记为

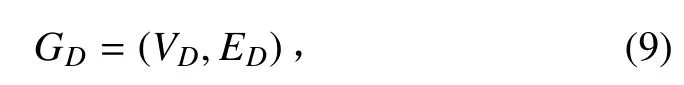
STCN 是一个支持对二元时间约束系统进行描述和推理的通用模型，并能够在多项式时间内检测出一致性结果。STCN 同样包括一组时间点变量

和一组约束

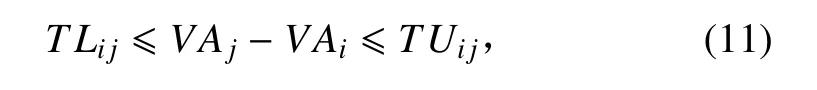
其中：

该约束还可以表示为一对不等式的形式

这样，求解 STCSP 可归结为求解一组关于 VAi的线性不等式。距离图GD中的顶点仍是时间点的集合，边 VAi→VAj标注权值 TUij，表示线性不等式

边 VAj→VAi标注权值 −TLij，表示线性不等式

如图1 所示。

例如，假定突击组对既定目标的突击开始时间为TR+40 min，结束时间为 TR+55 min，突击动作至少持续10 min。将空中编队开始行动作为一个虚拟的协同动作，其中时间 TR为参照时间，即 TR=0。那么，该动作时间约束可通过以不等式(16)等价描述。

图1　两顶点 STCN 示意图Fig. 1　STCN of 2 vertices

根据 STCN 的定义，式(16)可转化为图所示的STCN。

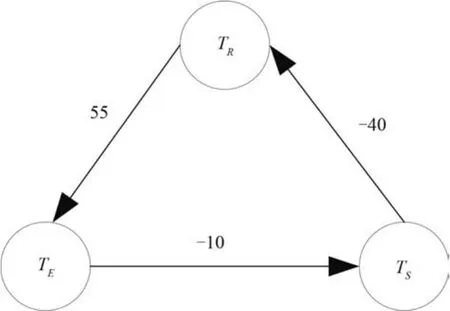
图2　突击动作的 STCNFig. 2　STCN of assault

借鉴图论中邻接矩阵的思想[6]，可将 STCN 表示为权值矩阵的形式。

定义5 STCN 的权值矩阵：称矩阵

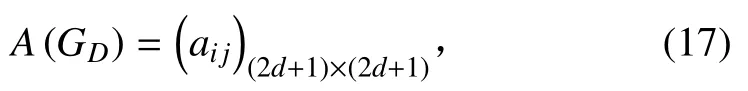
为 d 个协同动作组成的 STCN —— GD的权值矩阵，

其中

式中：Wij为有向边 i→j 的权重，且 Wij为实数。

3　基于时间约束网络的时间协同模型

3.1时间约束的定量计算

要建立协同动作的时间协同 STCN 模型，不但需要研究动作间的时间约束关系的描述方法，还要进行时间的定量计算。对于整个作战进程而言，未知的和难以估计的因素较多，要精确确定航空兵各编组协同动作的定量时间约束关系非常困难。

为综合各种影响因素，采用三点时间估计法计算动作间的定量时间约束关系[4,8]。三点时间估计法是估计协同动作时间约束的三种时间（乐观时间、最可能时间、悲观时间），然后计算它们的平均时间作为该动作的定量时间约束。

以协同动作 CAki的开始时间 TS（CAki） 为例，说明估计的三种时间：

乐观时间：在顺利的情况下，协同动作 CAki开始的时间，用 TSa（CAki） 表示。

最可能时间：在正常情况下，协同动作 CAdi开始的时间，用 TSm（CAdi） 表示。

悲观时间：在不顺利的情况下，协同动作 CAdi开始的时间，用 TSb（CAdi） 表示。

显然，以上三种时间都具有一定发生的概率。根据经验，这些时间的概率分布可以认为近似于正态分布，一般情况下可按下列公式计算定量时间约束

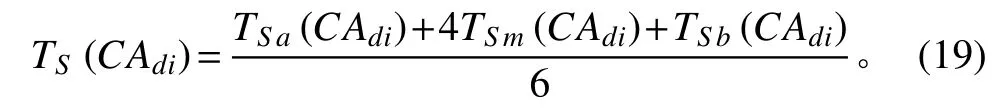
协同动作 CAdi的结束时间 TE（CAdi）、至少持续时间 TDur（CAdi），以及 CAdi与 CAdj间的最小间隔时间 TD（CAdi，CAdj） 皆可参照以上方法依次计算得到。

3.2时间协同模型的建立

确定协同动作间的定量时间约束关系之后，只需将定量时间约束转化为 STCN 要求的不等式形式，再根据相关定义即可建立协同动作时间协同 STCN 模型。

以 2 个协同动作为例，建立时间协同 STCN 模型。

假定 CA1，CA2为航空兵对海打击过程中，编组协同动作集 CA 中的 2 个协同动作，且 CA1，CA2为时间区间对象。根据协同要求，CA1，CA2间的时间约束关系为时序约束，且为 13 种 Ⅱ 关系中的第 2 种情况，即 CA1before CA2，转化成时间点约束为

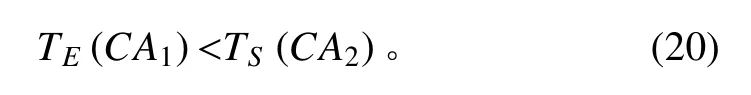
经定量计算得：动作 CA1开始时间为 TS（CA1），结束时间为 TE（CA1），至少持续时间 TDur（CA1）；动作 CA2开始时间为 TS（CA2），结束时间为TE（CA1），至少持续时间为 TDur（CA2；动作 CA1应在动作 CA2开始之前 TD（CA1，CA2） 个时间单位完成。令

为基准时间，则动作 CA1和 CA2之间的时间约束关系如式 (22) 所示的一组线性不等式。

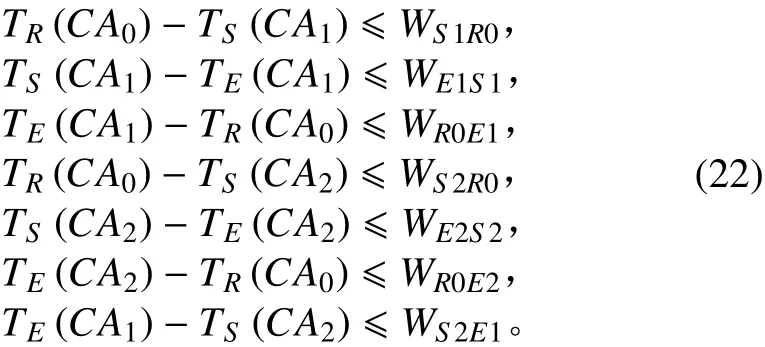
则根据STCN定义，CA1，CA2时间协同 STCN 模型如图3 所示。

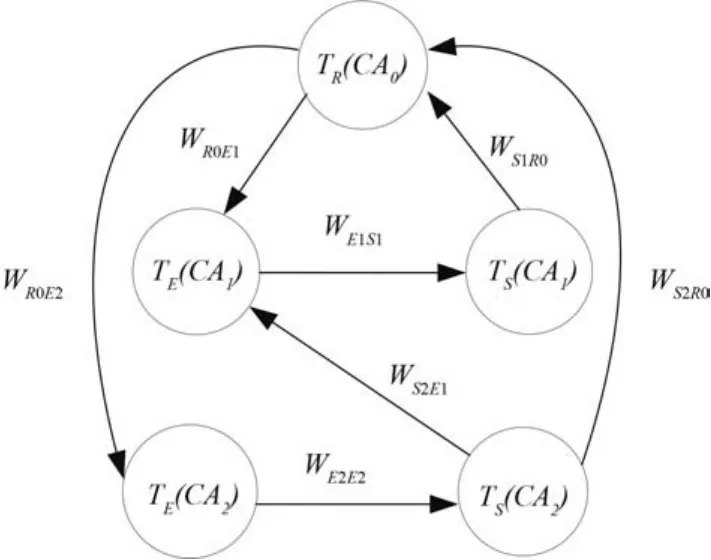
图3　两动作的 STCN 模型Fig. 3　STCN model of 2 actions

由以上示例可知，时间协同 STCN 模型建模的具体流程见图4。

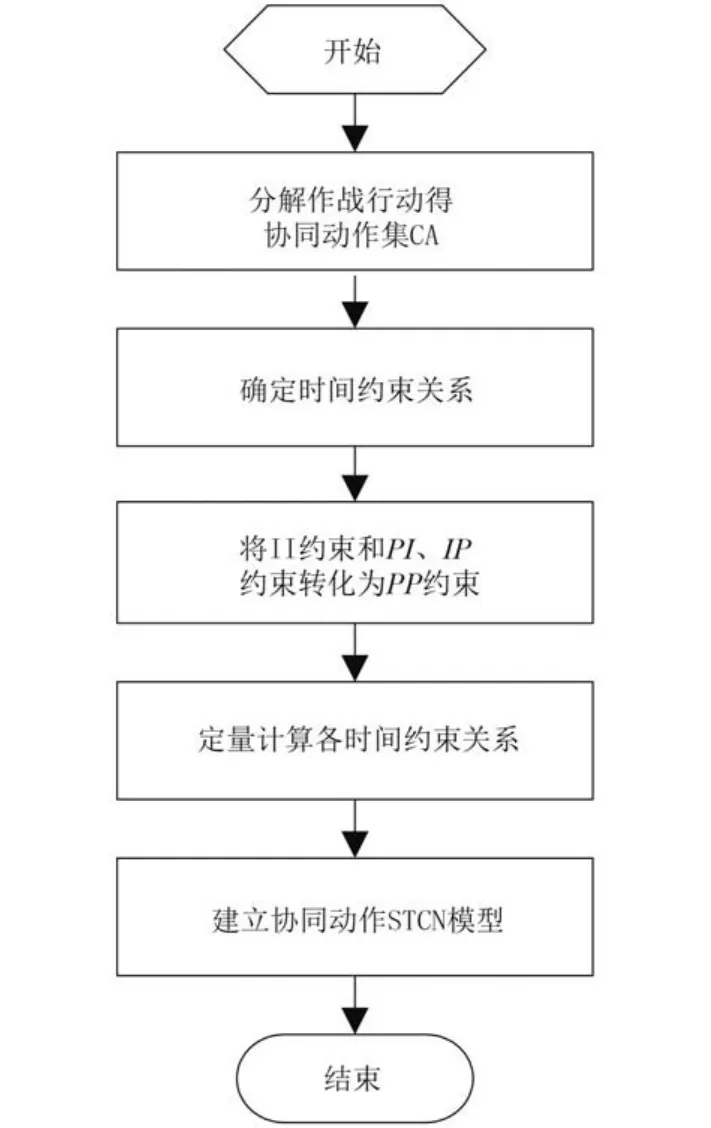
图4　时间协同模型建立流程Fig. 4　Flow of time coordination model establishment

根据以上流程可建立的 d 个协同动作组成的 STCN模型，其示意图如图5 所示。

图5　个协同动作 STCN 模型示意图Fig. 5　STCN model of　actions

4　结语

本文建立了航空兵对海打击的协同动作 STCN 模型，这是航空兵时间协同研究的重要内容之一，下一步将应用该模型来检测处理初始情况下时间协同中存在的冲突，进行冲突消解。

参考文献：

[1]ALLEN J. Maintaining knowledge about temporal intervals[J]. Communications of the ACM, 1983, 26(11): 832–843.

[2]龙涛, 沈林成, 朱华勇, 等. 面向协同任务的多UCAV分布式任务分配与协调技术[J]. 自动化学报, 2007, 33(7): 731–737. LONG Tao, SHEN Lin-cheng, ZHU Hua-yong, et al. Distributed task allocation &coordination technique of multiple UCAVs for cooperative tasks[J]. Acta automatica sinica, 2007, 33(7): 731–737.

[3]刘卫东, 高立娥, 徐德民, 等. 水下航行器控制系统实时多任务调度[J]. 探测与控制学报, 2002, 24(3): 51–54. LIU Wei-dong, GAO Li-e, XU De-min, et al. Real-time multitask scheduling for underwater vehicle control system[J]. Journal of detection & control, 2002, 24(3): 51–54.

[4]《运筹学》教材编写组. 运筹学[M]. 北京: 清华大学出版社, 2000.

[5]李永峰, 周兴社, 杜可君, 等. 基于时间约束网络的智能活动规划[J]. 计算机科学, 2011, 38(2): 179–183. LI Yong-feng, ZHOU Xing-she, DU Ke-jun, et al. Activity planning based on temporal constraint network[J]. Computer science, 2011, 38(2): 179–183.

[6]王树禾. 图论[M]. 2版. 北京: 科学出版社, 2009 (请核对年份)

[7]徐文胜, 熊光楞, 肖田元. 并行工程中时间约束网络建立及冲突检测研究[J]. 系统仿真学报, 2003, 15(2): 185–189. XU Wen-sheng, XIONG Guang-leng, XIAO Tian-yuan, et al. Research on establishment of temporal constraint network and conflict detection in concurrent engineering[J]. Acta simulata systematica sinica, 2003, 15(2): 185–189.

[8]DASDAN A. Provably efficient algorithms for resolving temporal and spatial difference constraint violations[J]. ACM Transactions on Design Automation of Electronic Systems, 2009, 14(1). DOI: 10.1145/1455229.1455237.

Research on the Time constraint Model of Aviation Air to Sea Cooperative Operation

MA Hai-yang1, LI Dong1, SUN Huai-liang2
(1. Naval Aeronautical Engineering Institute, Yantai 264001; 2. Yellow Sea Fisheries Research Institute,QingDao, 266000)

Abstract:Time factor become more and more important in the cooperative operations. Firstly, STCN was analyzed, and then, according to the STCN, quantified aviation cooperative time constraint, turned TC into inequality that STCN required, the process of time cooperative model of STCN was given. Finally, model of d actions was built based on STCN.

Key words:aviation；cooperative actions；TCN；time constraint model

作者简介:马海洋(1985–)，男，博士研究生，研究方向为海军兵种作战数理战术分析。

收稿日期:2015–08–16； 修回日期: 2015–06–05

文章编号：1672–7619(2016)03–0147–04

doi：10.3404/j.issn.1672–7619.2016.03.031

中图分类号：E917

文献标识码：A